4.3.3 十字相乘法分解因式 课件 2022-2023学年北师大版八年级数学下册
文档属性
| 名称 | 4.3.3 十字相乘法分解因式 课件 2022-2023学年北师大版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 399.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 09:52:14 | ||
图片预览





文档简介
(共17张PPT)
十字相乘法,分组分解法
第四章 因式分解
知识回顾(2分钟)
计算:
(1)
(2)
(3)
(4)
思考,怎样将下列因式分解:
(1)
(2)
(3)
(4)
=
=
=
=
?
学习目标(1分钟)
1、理解并掌握十字相乘法分解因式;
2、理解并掌握分组分解法分解因式。
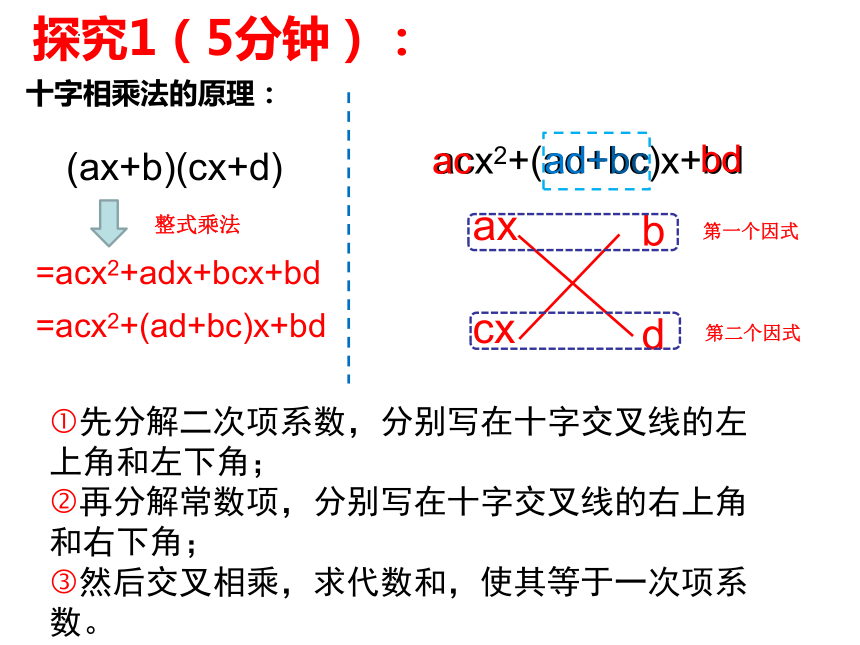
十字相乘法的原理:
(ax+b)(cx+d)
整式乘法
=acx2+adx+bcx+bd
=acx2+(ad+bc)x+bd
acx2+(ad+bc)x+bd
ac
ax
cx
bd
b
d
ad+bc
第一个因式
第二个因式
先分解二次项系数,分别写在十字交叉线的左上角和左下角;
再分解常数项,分别写在十字交叉线的右上角和右下角;
然后交叉相乘,求代数和,使其等于一次项系数。
探究1(5分钟):
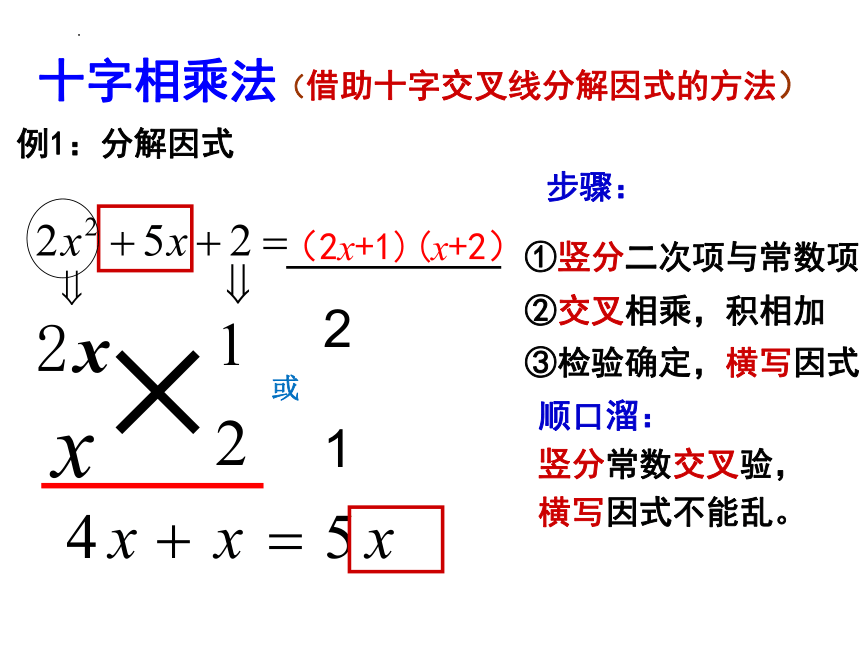
例1:分解因式
步骤:
①竖分二次项与常数项
②交叉相乘,积相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:
竖分常数交叉验,
横写因式不能乱。
(2x+1)(x+2)
2
1
或
十字相乘法:
对于二次三项式的分解因式,借用一个十字交叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x +(p+q)x+pq=(x+p)(x+q)
2
x
x
p
q
px+qx=(p+q)x
x
2
pq
2.填空:在横线上填+、-符号
=(x 3)(x 1)
+
+
=(x 2)(x 1)
-
-
=(y 2)(y 3)
+
-
=(t 3)(t 6)
-
+
1.以下多项式中分解因式为 的多项式是
( )
A.
B.
C.
D.
C
同步训练1:(8分钟)
3.用适当的方法分解因式;
(x-2)(x-3)
(x+3)(x+4)
(t-2)(t+3)
(m+2)(m-5)
-(y+8)(y-2)
(易错点)当二次项系数为-1时,先提出负号再因式分解
分解因式:(x2﹣x)2+(x2﹣x)﹣6.
解:设X2﹣X=y
=y2+y﹣6
=(y+3)(y-2)
=(x2-x+3)(x2-x-2
=(x2-x+3)(x+1)(x-2)
换元法
解:原式=(x2﹣x+3)(x2﹣x﹣2)
=(x2﹣x+3)(x+1)(x﹣2).
整体法:把(x2-x)看成一个整体,然后再根据十字相乘法分解因式
探究2
将一个多项式分组后,可提公因式或运用公式继续分解
的方法是因式分解中的分组分解法,一般的分组分解法
有四种形式,即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等。
“2+3”分法:
“2+2”分法:
ax+ay+bx+by
解:原式=(ax+ay)+(bx+by)
=a(x+y)+b(x+y)
=(x+y)(a+b)
a2+2ab+b2+a2-b2
解:原式=(a+b)2(a+b)(a-b)
=(a+b)(a+b+a-b)
=2a(a+b)
请用分组分解法分解因式a2 b2+a2b ab2.
解:原式=(a2 b2)+(a2b ab2)
=(a+b)(a b)+ab(a b)
=(a b)(a+b+ab)
“3+1”分法:
“3+3”分法:
a2+2ab+b2-x2
解:原式=(a+b)2-x2
=(a+b+x)(a+b-x)
a2+2ab+b2-a2x-2abx-b2x
解:原式=(a+b)2-(a2x+2abx+b2x)
=(a+b)2-x(a+b)2
=(a+b)2(1-x)
同步训练2:
用适当的方法将下列各式因式分解.
(1)m2 mn+mx nx (2)x2 y2 x y
(1)解:原式=(m2-mn)+(mx nx)
=m(m n)+x(m n)
=(m n)(m+x)
(3)9m2 4x2+4xy y2
(2)解:原式=(x2 y2) (x+y)
=(x+y)(x y) (x+y)
=(x+y)(x y 1)
(3)解:原式=9m2 (4x2 4xy+y2)
=(3m)2 (2x y)2
=(3m+2x y)(3m 2x+y)
先阅读下面的材料,再解决问题:
要把多项式
因式分解,可以先把它的前两项分成一组,并提出
;把它的后两项分成一组,并提出
,从而得到
,这时 又有因式
,于是可提公因式
,从而得到
.因此有
.这种因式分解的方法叫做分组分解法.
在三角形中,若任意两条边的差均为0,则这个三角形是等边三角形;若只有两条边的差为0,则这个三角形是等腰三角形;若有两条边的平方和与第三边的平方的差为0,则这个三角形是直角三角形。
请用上面材料中提供的方法解决问题:
(1)将多项式
分解因式;
(2)若
的三边
、
、
满足条件:
,试判断
的形状.
解:(1)ab-ac+b2-bc
=(ab-ac)+(b2-bc)
=a(b-c)+b(b-c)
=(a+b)(b-c);
(2)由已知,得
(a2-b2)(a2+b2)+c2(a2+b2)=0.
即(a2+b2)(a2-b2+c2)=0
∵a2+b2>0
∴a2-b2+c2=0
即 a2+c2=b2
∴△ABC是直角三角形.
2.分解因式
(1)2x2﹣7x+3=
(2x﹣1)(x﹣3)
1.如果ax2+bx+c=(2x﹣3)(x+4),则a= ,
b= ,c= .
2
-12
5
(2)2x3﹣6x2+4x=
2x(x﹣1)(x﹣2)
3.已知多项式x2﹣4x+m分解因式的结果为(x+a)(x﹣6),求2a﹣m的值.
解:由题意得:
x2﹣4x+m=(x+a)(x﹣6)
=x2+(a﹣6)x﹣6a,
∴a﹣6=﹣4,m=﹣6a.
∴a=2,m=﹣12.
∴2a﹣m=2×2+12=16.
巩固练习:(15分钟)
小结:
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
1.十字相乘法:对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x +(p+q)x+pq=(x+p)(x+q)
2
易错点:当二次项系数为-1时,先提出负号再因式分解
2.分组分解法:先将一个多项式分组后,再用提公因式或公式法继续分解的方法叫做分组分解法。
十字相乘法,分组分解法
第四章 因式分解
知识回顾(2分钟)
计算:
(1)
(2)
(3)
(4)
思考,怎样将下列因式分解:
(1)
(2)
(3)
(4)
=
=
=
=
?
学习目标(1分钟)
1、理解并掌握十字相乘法分解因式;
2、理解并掌握分组分解法分解因式。
十字相乘法的原理:
(ax+b)(cx+d)
整式乘法
=acx2+adx+bcx+bd
=acx2+(ad+bc)x+bd
acx2+(ad+bc)x+bd
ac
ax
cx
bd
b
d
ad+bc
第一个因式
第二个因式
先分解二次项系数,分别写在十字交叉线的左上角和左下角;
再分解常数项,分别写在十字交叉线的右上角和右下角;
然后交叉相乘,求代数和,使其等于一次项系数。
探究1(5分钟):
例1:分解因式
步骤:
①竖分二次项与常数项
②交叉相乘,积相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:
竖分常数交叉验,
横写因式不能乱。
(2x+1)(x+2)
2
1
或
十字相乘法:
对于二次三项式的分解因式,借用一个十字交叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x +(p+q)x+pq=(x+p)(x+q)
2
x
x
p
q
px+qx=(p+q)x
x
2
pq
2.填空:在横线上填+、-符号
=(x 3)(x 1)
+
+
=(x 2)(x 1)
-
-
=(y 2)(y 3)
+
-
=(t 3)(t 6)
-
+
1.以下多项式中分解因式为 的多项式是
( )
A.
B.
C.
D.
C
同步训练1:(8分钟)
3.用适当的方法分解因式;
(x-2)(x-3)
(x+3)(x+4)
(t-2)(t+3)
(m+2)(m-5)
-(y+8)(y-2)
(易错点)当二次项系数为-1时,先提出负号再因式分解
分解因式:(x2﹣x)2+(x2﹣x)﹣6.
解:设X2﹣X=y
=y2+y﹣6
=(y+3)(y-2)
=(x2-x+3)(x2-x-2
=(x2-x+3)(x+1)(x-2)
换元法
解:原式=(x2﹣x+3)(x2﹣x﹣2)
=(x2﹣x+3)(x+1)(x﹣2).
整体法:把(x2-x)看成一个整体,然后再根据十字相乘法分解因式
探究2
将一个多项式分组后,可提公因式或运用公式继续分解
的方法是因式分解中的分组分解法,一般的分组分解法
有四种形式,即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等。
“2+3”分法:
“2+2”分法:
ax+ay+bx+by
解:原式=(ax+ay)+(bx+by)
=a(x+y)+b(x+y)
=(x+y)(a+b)
a2+2ab+b2+a2-b2
解:原式=(a+b)2(a+b)(a-b)
=(a+b)(a+b+a-b)
=2a(a+b)
请用分组分解法分解因式a2 b2+a2b ab2.
解:原式=(a2 b2)+(a2b ab2)
=(a+b)(a b)+ab(a b)
=(a b)(a+b+ab)
“3+1”分法:
“3+3”分法:
a2+2ab+b2-x2
解:原式=(a+b)2-x2
=(a+b+x)(a+b-x)
a2+2ab+b2-a2x-2abx-b2x
解:原式=(a+b)2-(a2x+2abx+b2x)
=(a+b)2-x(a+b)2
=(a+b)2(1-x)
同步训练2:
用适当的方法将下列各式因式分解.
(1)m2 mn+mx nx (2)x2 y2 x y
(1)解:原式=(m2-mn)+(mx nx)
=m(m n)+x(m n)
=(m n)(m+x)
(3)9m2 4x2+4xy y2
(2)解:原式=(x2 y2) (x+y)
=(x+y)(x y) (x+y)
=(x+y)(x y 1)
(3)解:原式=9m2 (4x2 4xy+y2)
=(3m)2 (2x y)2
=(3m+2x y)(3m 2x+y)
先阅读下面的材料,再解决问题:
要把多项式
因式分解,可以先把它的前两项分成一组,并提出
;把它的后两项分成一组,并提出
,从而得到
,这时 又有因式
,于是可提公因式
,从而得到
.因此有
.这种因式分解的方法叫做分组分解法.
在三角形中,若任意两条边的差均为0,则这个三角形是等边三角形;若只有两条边的差为0,则这个三角形是等腰三角形;若有两条边的平方和与第三边的平方的差为0,则这个三角形是直角三角形。
请用上面材料中提供的方法解决问题:
(1)将多项式
分解因式;
(2)若
的三边
、
、
满足条件:
,试判断
的形状.
解:(1)ab-ac+b2-bc
=(ab-ac)+(b2-bc)
=a(b-c)+b(b-c)
=(a+b)(b-c);
(2)由已知,得
(a2-b2)(a2+b2)+c2(a2+b2)=0.
即(a2+b2)(a2-b2+c2)=0
∵a2+b2>0
∴a2-b2+c2=0
即 a2+c2=b2
∴△ABC是直角三角形.
2.分解因式
(1)2x2﹣7x+3=
(2x﹣1)(x﹣3)
1.如果ax2+bx+c=(2x﹣3)(x+4),则a= ,
b= ,c= .
2
-12
5
(2)2x3﹣6x2+4x=
2x(x﹣1)(x﹣2)
3.已知多项式x2﹣4x+m分解因式的结果为(x+a)(x﹣6),求2a﹣m的值.
解:由题意得:
x2﹣4x+m=(x+a)(x﹣6)
=x2+(a﹣6)x﹣6a,
∴a﹣6=﹣4,m=﹣6a.
∴a=2,m=﹣12.
∴2a﹣m=2×2+12=16.
巩固练习:(15分钟)
小结:
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
1.十字相乘法:对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x +(p+q)x+pq=(x+p)(x+q)
2
易错点:当二次项系数为-1时,先提出负号再因式分解
2.分组分解法:先将一个多项式分组后,再用提公因式或公式法继续分解的方法叫做分组分解法。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
