26.3 二次函数y=ax? bx c的图象 第1课时 课件(共32张PPT)
文档属性
| 名称 | 26.3 二次函数y=ax? bx c的图象 第1课时 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 10:12:27 | ||
图片预览










文档简介
(共32张PPT)
26.3二次函数y=ax +bx+c的图象(第1课时)
第26章 二次函数
教师
xxx
沪教版 九年级第一学期
二次函数y=ax +bx+c的图象和性质
01
02
CONTANTS
目 录
二次函数y=ax +bx+c的图象和性质
01
1.说出二次函数y=a(x-h)2+k的图象和性质?
2.平移规律?
上加下减,左加右减
复习引入
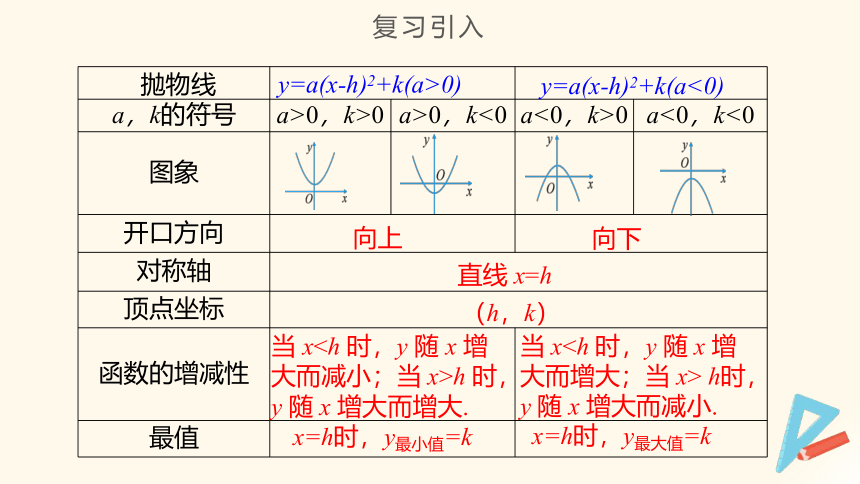
a,k的符号 a>0,k>0 a>0,k<0 a<0,k>0 a<0,k<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
直线 x=h
(h,k)
当 xh 时,y 随 x 增大而增大.
当 x h时,y 随 x 增大而减小.
x=h时,y最小值=k
x=h时,y最大值=k
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
抛物线
复习引入
我们已经知道二次函数y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论二次函数 图象和性质 怎样将 转换成y=a(x-h)2+k形式?
配方
探究新知
如何配方?
1、“提”:提出二次项系数;
2、“配”:括号内配成完全平方;
3、“化”:化成顶点式.
顶点式
一般式
探究新知
练习:将下面的函数解析式改为顶点式
(1)y=x2-6x+10 (2)y=-4x2-16x+1
解:(1)y=x2-6x+10
=x2-6x+9-9+10
=(x-3)2+1
解: (2)y=-4x2-16x+1
=-4(x2+4x)+1
=-4(x2+4x+4-4)+1
=-4(x+2)2+16+1
=-4(x+2)2+17
探究新知
由配方的结果可知, 的顶点是(6,3),对称轴是x=6.
因此, 的顶点是(6,3),对称轴是x=6.
探究新知
思考:1.怎样将 化成y=a(x-h)2+k的形式?
【点拨】二次函数一般式化为顶点式的步骤:(1)“提”:提出二次项系数;(2)“配”:括号内配成完全平方式;(3)“化”:化成顶点式.
探究新知
2.你能说出 的对称轴及顶点坐标吗?
对称轴是直线x=6,顶点坐标是(6,3).
3.二次函数 可以看作是由 怎样平移得到的?
平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
(6,3)
探究新知
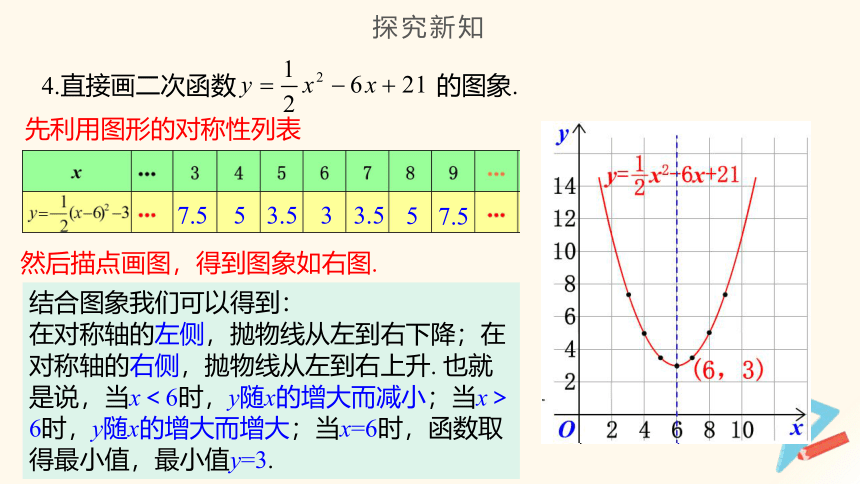
4.直接画二次函数 的图象.
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
然后描点画图,得到图象如右图.
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升. 也就是说,当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大;当x=6时,函数取得最小值,最小值y=3.
探究新知
探究:你能用前面的方法讨论二次函数 的图象和性质吗?
配方
开口向下
顶点是(-1,3)
对称轴是直线x=-1
与y轴交点(0,1)
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右上升;在对称轴的右侧,抛物线从左到右下降. 也就是说,当x<-1时,y随x的增大而增大;当x>-1时,y随x的增大而减小;当x=-1时,函数取得最大值,最大值y=3.
探究新知
一般地,二次函数y=ax2+bx+c(a≠0) 可以通过配方化成y=a(x-h)2+k的形式(顶点式).
探究新知
配 方
对称轴是直线 ,顶点是 .
如果a>0时,那么当 时,y最小值= ;
如果a<0时,那么当 时,y最大值= .
归纳总结
探究新知
如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大;
如果a<0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
归纳总结
探究新知
写出下列抛物线的开口方向、对称轴和顶点:
向上
向下
向下
向上
直线x=-
直线x=-1
直线x=2
直线x=4
(-,-)
(-1,1)
(2,0)
(4,-5)
探究新知
例1.已知抛物线y=2x2-12x+13.
(1)当x为何值时,y有最小值,最小值是多少?
(2)当x为何值时,y随x的增大而减小;
(3)将该抛物线向右平移2个单位,再向上平移2个单位,请直接写出新抛物线的表达式.
解:∵y=2x2-12x+13=2(x2-2x+9)-5=2(x-3)2-5,
∴抛物线开口向上,顶点为(3,-5),对称轴为直线x=3.
(1)当x=3时,y有最小值,最小值为-5;
(2)当x<3时,y随x的增大而减小;
(3)新抛物线的表达式为y=2(x-5)2-3.
典型例题
图形 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
x
y
O
y
x
归纳总结
探究新知
二次函数y=ax2+bx+c的补充性质
1.关于x轴对称的抛物线解析式为 y=-(ax2+bx+c)= -ax2-bx-c
2.关于y轴对称的抛物线解析式为y=a(-x)2+b(-x)+c=ax2-bx+c
3.当 时,顶点在y轴上。
4.当Δ=b2-4ac=0时,顶点在x轴上,当Δ=b2-4ac>0时 ,抛物线与x轴有两个交点,当Δ=b2-4ac<0时,抛物线与x轴没有交点。
5.当x=1时,抛物线解析式为y=a+b+c;当x=-1时,抛物线解析式为y=a-b+c
归纳总结
探究新知
1.把抛物线y=x2+bx+c的图象向右平移3个单位长度,再向下平移2个单位长度,所得图象的解析式为y=x2-3x+5,则( )
A.b=3,c=7 B.b=6,c=3
C.b=-9,c=-5 D.b=-9,c=21
A
课堂练习
2.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是( )
A.abc<0,b2-4ac>0
B.abc>0,b2-4ac>0
C.abc<0,b2-4ac<0
D.abc>0,b2-4ac<0
B
课堂练习
3.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
C
课堂练习
4.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的表达式是( )
A. B.
C. D.
A
课堂练习
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).其中结论正确的个数是( )
A.1
B.2
C.3
D.4
C
课堂练习
6.把二次函数y=-2x2-4x+1配成y=a(x-h)2+k的形式为_________________,所以其图象的开口向___,对称轴是直线________,顶点坐标为_________.
y=-2(x+1)2+3
下
x=-1
(-1,3)
课堂练习
7.已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(1)求b,c满足的关系式;
(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;
课堂练习
解:(1)将点(-2,4)的坐标代入y=x2+bx+c,得4-2b+c=4,∴c=2b.
(2)由题知,m=-,n=,
∴b=-2m.
又由(1)知c=2b,
∴n=.
∴n=-m2-4m.
课堂练习
8.如图,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0).
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时, 求点P的坐标.
解:(1)把点B(3,0)的坐标代入y=-x2+mx+3得:
0=-32+3m+3,
解得m=2,
∴y=-x2+2x+3=-(x-1)2+4. ∴顶点坐标为(1,4).
课堂练习
(2)如图,连接BC交抛物线的对称轴l于点P,则此时PA+PC的值最小.
设直线BC的函数解析式为y=kx+b,
∵C(0,3),B(3,0),
∴
解得
∴直线BC的函数解析式为y=-x+3.当x=1时,y=-1+3=2,
∴当PA+PC的值最小时,点P的坐标为(1,2).
课堂练习
图象
性质
解析式
开口方向
抛物线
顶点
对称轴
增减性
待定系数法
顶点式与一般式的联系
y=ax2+bx+c
的图象和性质
课堂小结
感谢观看
26.3二次函数y=ax +bx+c的图象(第1课时)
第26章 二次函数
教师
xxx
沪教版 九年级第一学期
二次函数y=ax +bx+c的图象和性质
01
02
CONTANTS
目 录
二次函数y=ax +bx+c的图象和性质
01
1.说出二次函数y=a(x-h)2+k的图象和性质?
2.平移规律?
上加下减,左加右减
复习引入
a,k的符号 a>0,k>0 a>0,k<0 a<0,k>0 a<0,k<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
直线 x=h
(h,k)
当 x
当 x
x=h时,y最小值=k
x=h时,y最大值=k
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
抛物线
复习引入
我们已经知道二次函数y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论二次函数 图象和性质 怎样将 转换成y=a(x-h)2+k形式?
配方
探究新知
如何配方?
1、“提”:提出二次项系数;
2、“配”:括号内配成完全平方;
3、“化”:化成顶点式.
顶点式
一般式
探究新知
练习:将下面的函数解析式改为顶点式
(1)y=x2-6x+10 (2)y=-4x2-16x+1
解:(1)y=x2-6x+10
=x2-6x+9-9+10
=(x-3)2+1
解: (2)y=-4x2-16x+1
=-4(x2+4x)+1
=-4(x2+4x+4-4)+1
=-4(x+2)2+16+1
=-4(x+2)2+17
探究新知
由配方的结果可知, 的顶点是(6,3),对称轴是x=6.
因此, 的顶点是(6,3),对称轴是x=6.
探究新知
思考:1.怎样将 化成y=a(x-h)2+k的形式?
【点拨】二次函数一般式化为顶点式的步骤:(1)“提”:提出二次项系数;(2)“配”:括号内配成完全平方式;(3)“化”:化成顶点式.
探究新知
2.你能说出 的对称轴及顶点坐标吗?
对称轴是直线x=6,顶点坐标是(6,3).
3.二次函数 可以看作是由 怎样平移得到的?
平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
(6,3)
探究新知
4.直接画二次函数 的图象.
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
然后描点画图,得到图象如右图.
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升. 也就是说,当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大;当x=6时,函数取得最小值,最小值y=3.
探究新知
探究:你能用前面的方法讨论二次函数 的图象和性质吗?
配方
开口向下
顶点是(-1,3)
对称轴是直线x=-1
与y轴交点(0,1)
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右上升;在对称轴的右侧,抛物线从左到右下降. 也就是说,当x<-1时,y随x的增大而增大;当x>-1时,y随x的增大而减小;当x=-1时,函数取得最大值,最大值y=3.
探究新知
一般地,二次函数y=ax2+bx+c(a≠0) 可以通过配方化成y=a(x-h)2+k的形式(顶点式).
探究新知
配 方
对称轴是直线 ,顶点是 .
如果a>0时,那么当 时,y最小值= ;
如果a<0时,那么当 时,y最大值= .
归纳总结
探究新知
如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大;
如果a<0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
归纳总结
探究新知
写出下列抛物线的开口方向、对称轴和顶点:
向上
向下
向下
向上
直线x=-
直线x=-1
直线x=2
直线x=4
(-,-)
(-1,1)
(2,0)
(4,-5)
探究新知
例1.已知抛物线y=2x2-12x+13.
(1)当x为何值时,y有最小值,最小值是多少?
(2)当x为何值时,y随x的增大而减小;
(3)将该抛物线向右平移2个单位,再向上平移2个单位,请直接写出新抛物线的表达式.
解:∵y=2x2-12x+13=2(x2-2x+9)-5=2(x-3)2-5,
∴抛物线开口向上,顶点为(3,-5),对称轴为直线x=3.
(1)当x=3时,y有最小值,最小值为-5;
(2)当x<3时,y随x的增大而减小;
(3)新抛物线的表达式为y=2(x-5)2-3.
典型例题
图形 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
x
y
O
y
x
归纳总结
探究新知
二次函数y=ax2+bx+c的补充性质
1.关于x轴对称的抛物线解析式为 y=-(ax2+bx+c)= -ax2-bx-c
2.关于y轴对称的抛物线解析式为y=a(-x)2+b(-x)+c=ax2-bx+c
3.当 时,顶点在y轴上。
4.当Δ=b2-4ac=0时,顶点在x轴上,当Δ=b2-4ac>0时 ,抛物线与x轴有两个交点,当Δ=b2-4ac<0时,抛物线与x轴没有交点。
5.当x=1时,抛物线解析式为y=a+b+c;当x=-1时,抛物线解析式为y=a-b+c
归纳总结
探究新知
1.把抛物线y=x2+bx+c的图象向右平移3个单位长度,再向下平移2个单位长度,所得图象的解析式为y=x2-3x+5,则( )
A.b=3,c=7 B.b=6,c=3
C.b=-9,c=-5 D.b=-9,c=21
A
课堂练习
2.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是( )
A.abc<0,b2-4ac>0
B.abc>0,b2-4ac>0
C.abc<0,b2-4ac<0
D.abc>0,b2-4ac<0
B
课堂练习
3.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
C
课堂练习
4.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的表达式是( )
A. B.
C. D.
A
课堂练习
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).其中结论正确的个数是( )
A.1
B.2
C.3
D.4
C
课堂练习
6.把二次函数y=-2x2-4x+1配成y=a(x-h)2+k的形式为_________________,所以其图象的开口向___,对称轴是直线________,顶点坐标为_________.
y=-2(x+1)2+3
下
x=-1
(-1,3)
课堂练习
7.已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(1)求b,c满足的关系式;
(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;
课堂练习
解:(1)将点(-2,4)的坐标代入y=x2+bx+c,得4-2b+c=4,∴c=2b.
(2)由题知,m=-,n=,
∴b=-2m.
又由(1)知c=2b,
∴n=.
∴n=-m2-4m.
课堂练习
8.如图,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0).
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时, 求点P的坐标.
解:(1)把点B(3,0)的坐标代入y=-x2+mx+3得:
0=-32+3m+3,
解得m=2,
∴y=-x2+2x+3=-(x-1)2+4. ∴顶点坐标为(1,4).
课堂练习
(2)如图,连接BC交抛物线的对称轴l于点P,则此时PA+PC的值最小.
设直线BC的函数解析式为y=kx+b,
∵C(0,3),B(3,0),
∴
解得
∴直线BC的函数解析式为y=-x+3.当x=1时,y=-1+3=2,
∴当PA+PC的值最小时,点P的坐标为(1,2).
课堂练习
图象
性质
解析式
开口方向
抛物线
顶点
对称轴
增减性
待定系数法
顶点式与一般式的联系
y=ax2+bx+c
的图象和性质
课堂小结
感谢观看
