4.1 线段、射线、直线-2023-2024学年七年级数学上册同步精品课件(北师大版)
文档属性
| 名称 | 4.1 线段、射线、直线-2023-2024学年七年级数学上册同步精品课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览







文档简介
北师大版 数学 七年级上册
1 线段、射线、直线
第四章 基本平面图形
学习目标
1.在现实情境中理解线段、射线、直线的概念及他们的区别与联系.(重点)
2.会用不同的方法表示线段、射线、直线.(难点)
3.了解“两点确定一条直线”的几何事实.
一、导入新课
丰富的图形世界是由一些简单的图形构成的,观察下列图片,你能看到哪些平面图形?你知道它们是如何构成的吗?
一、导入新课
绷紧的琴弦,手电筒射出的光线,向两方无限延伸的笔直的铁轨等,它们可以分别抽象出哪些简单的平面图形呢?
线段、射线和直线.
二、新知探究
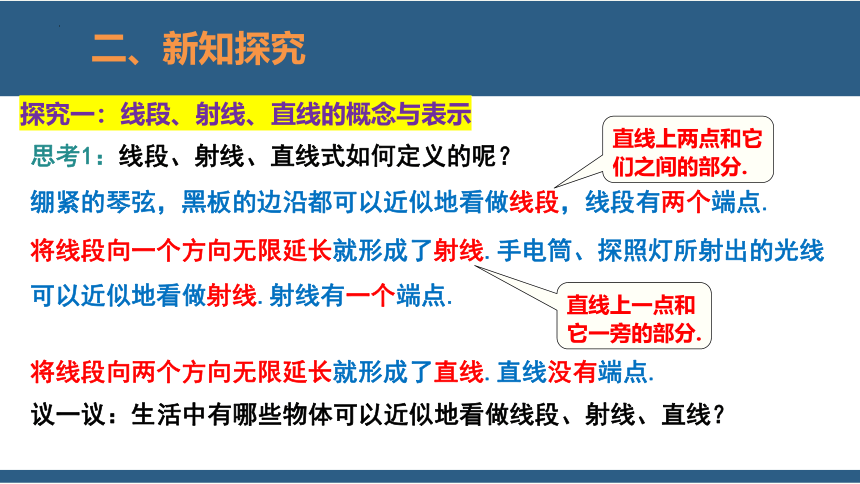
探究一:线段、射线、直线的概念与表示
绷紧的琴弦,黑板的边沿都可以近似地看做线段,线段有两个端点.
将线段向一个方向无限延长就形成了射线.手电筒、探照灯所射出的光线可以近似地看做射线.射线有一个端点.
将线段向两个方向无限延长就形成了直线.直线没有端点.
议一议:生活中有哪些物体可以近似地看做线段、射线、直线?
直线上两点和它们之间的部分.
直线上一点和它一旁的部分.
思考1:线段、射线、直线式如何定义的呢?
二、新知探究
思考2:怎么表示线段、射线、直线呢?
A
B
表示1: 线段 AB(或线段BA)
a
表示2:线段 a
表示:射线 OM
E
F
表示1:直线 EF(或直线FE)
表示2:直线l
M
O
l
线段的表示:用线段的两个端点字母表示,或用一个小写字母表示.
射线的表示:用端点和射线上另外一个点表示,端点必须写在前面.
直线的表示:用直线上任意两点表示,或用一个小写字母表示.
2.请分别表示出图中的线段、射线和直线。
A
B
C
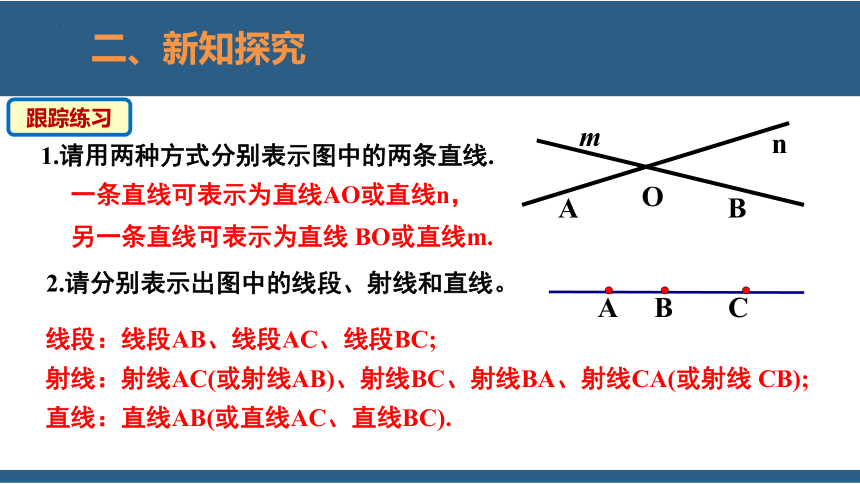
1.请用两种方式分别表示图中的两条直线.
B
A
O
m
n
二、新知探究
跟踪练习
线段:线段AB、线段AC、线段BC;
射线:射线AC(或射线AB)、射线BC、射线BA、射线CA(或射线 CB);
直线:直线AB(或直线AC、直线BC).
一条直线可表示为直线AO或直线n,另一条直线可表示为直线 BO或直线m.
二、新知探究
想一想:如图所示,射线OM与射线ON表示同一条射线吗?射线MN与射线NM呢?
解:因为射线OM与射线ON端点相同,延伸方向相同,
所以射线OM与射线ON表示同一条射线.
因为射线MN与射线NM端点不同,延伸方向相反,
所以射线MN与射线NM表示不同的射线.
2.如图所示,下列说法正确的是( )
A.直线AB和直线CD是不同的直线
B.射线AB和射线BA是同一条射线
C.线段AB和线段BA是同一条线段
D.以上说法均不正确
1.下列图形中表示射线AB的是( )
二、新知探究
跟踪练习
B
C
做一做:如图,已知平面上三点A、B、C.
(1)画线段AB;
(2)画直线BC;
(3)画射线CA;
解:(1)、(2)、(3)题如图所示.
(4)如何由线段AB得到射线AB和直线AB呢?
(4)将线段AB向B方向延伸得到射线AB,将线段AB向两个方向延伸得到直线AB.
(5)直线AB与直线BC有一个公共点B.
(5)直线AB与直线BC有几个公共点?
二、新知探究
二、新知探究
知识归纳
线段、射线与直线区别与联系:
特性
类别
图形
端点个数
是否可以延伸
是否可以量度
表示方法
作图描述
表示方法
备注
线段
两个
不可
延伸
可以
量度
线段AB或线段BA或线段a
A,B两点无序
连接AB
射线
一个
向一个方向延伸
不可以量度
射线AB
A,B两点有序,端点在前
以A为端点作射线AB
直线
无
向两个方向延伸
不可以量度
直线AB或直线
BA或直线a
A,B两点无序
过A,B两点作直线AB
二、新知探究
议一议:(1)图中共有几条线段?说明你分析这个问题的具体思路;
以A为端点的线段有AB,AC,AD,AE,共4条,以B为端点且与前面不重复的线段有BC,BD,BE,共3条,以C为端点且与前面不重复的线段有CD,CE,共2条,以D为端点且与前面不重复的线段有DE,共1条,从而共有4+3+2+1=10(条)线段.
1.当直线a上有1个点时,可得到 条射线, 条线段;
2.当直线a上有2个点时,可得到 条射线, 条线段;
3.当直线a上有3个点时,可得到 条射线, 条线段;
4.当直线a上有4个点时,可得到 条射线, 条线段;
5.当直线a上有5个点时,可得到 条射线, 条线段;
6.当直线a上有6个点时,可得到 条射线, 条线段;
议一议:(2)当直线a上有n个点时,可得到 条射线, 条线段.
·
B
·
·
A
O
a
·
C
二、新知探究
2
0
4
1
6
3
8
6
2n
n(n-1)
2
10
10
12
15
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
直线上有n个点时,有线段1+2+3+...+(n-1)=????(?????????)????(条).
?
二、新知探究
指出下图中线段、射线、直线分别有多少条?并把线段表示出来.
解:线段有3条,分别为线段AB、线段AC、线段BC.
射线有6条.
直线有1条.
自己尝试把6条射线画出来
跟踪练习
(2) 过两点A、B可以画几条直线?
A
B
做一做:(1) 过一点 O 可以画几条直线?
O
二、新知探究
探究二:直线的性质
过一点可以画无数条直线。
过两点可以画一条直线。
二、新知探究
(3)如果你想将一根细木条固定在墙上,至少需要几个钉子?这样做的依据是什么吗?
至少需要2个.
根据生活经验,我们发现:经过两点有且只有一条直线.
二、新知探究
直线的性质:
经过两点有且只有________条直线.
这一事实可以简述为:__________________.
一
两点确定一条直线
知识归纳
二、新知探究
下列现象:①农民伯伯拉绳插秧;②解放军叔叔打靶瞄准;③学生早操队列对齐;④在墙上至少要用两根钉子才能把木条固定;⑤改直弯曲的河道,缩短航程.其中可以用“两点确定一条直线”来解释的有__________.(填序号)
①②③④
跟踪练习
三、典例精析
解:(1)数轴可以看作规定了原点、正方向、单位长度的直线;
(2)数轴上原点及原点右边的部分是射线,这个图形表示成射线OB或射线OC;
(3)射线OB与射线OC是同一条射线,端点表示数0;
(4)射线AB 和射线BA是两条不同的射线,它们的端点不同,射线AB的端点是点A,射线BA的端点是点B;
(5)数轴上表示绝对值不大于2的部分是从表示 -2 的点到表示+2的点C的一条线段,可以表示为线段AC.
例1:如图,数轴上点O表示原点,点A 表示-2,点B表示1,点C表示2.
(1)数轴可以看作什么图形?
(2)数轴上原点及原点右边的部分是什么图形?这个图形怎样表示?
(3)射线OB 与射线OC是同一条射线吗?端点表示什么数?
(4)射线AB与射线BA是同一条射线吗?为什么?
5)数轴上表示绝对值不大于2的部分是什么图形?这个图形怎样表示?
三、典例精析
例2:小明发现,甲乙两地的火车路线上共有 10 个站,且任意两站之间的票价都不相同.请你帮他解决列问题:
(1)有多少种不同的票价?
(2)要准备多少种不同的车票?
(2)有多少种车票是要考虑顺序的,则有 45×2=90(种).
答:要准备 90种不同的车票.
解:(1)此题目相当于一条线段上有 10个点,有多少种不同的票价即有多少条线段.故不同的票价共有=????????×????????=45(种).
答:有45 种不同的票价.
?
2.如图所示,下列几何语句不正确的是( )
A.直线AB与直线BA是同一条直线 B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线 D.线段AB与线段BA是同一条线段
四、当堂练习
1.手电筒发射出来的光线,给我们的感觉是( )
A.线段 B.射线 C.直线 D.折线
B
C
3.图中直线AB,射线CD,线段MN能够相交的是( )
4.下列说法中,错误的是( )
A.经过一点的直线可以有无数条 B.经过两点的直线只有一条
C.一条直线只能用一个字母表示 D.线段EF与线段FE是同一条线段
C
四、当堂练习
D
5.如图所示,图中的直线可以表示为 或 .
7.如图所示,其中线段有_____条,射线有____条.
四、当堂练习
直线AB(或直线BA)
直线m
6.新学期开学整理教室时,老师总是先把每一列最前面和最后面的课桌摆好,然后依次摆中间的课桌,一会儿一列课桌就整齐地摆在一条直线上了,这是因为__________________.
两点确定一条直线
3
8
8.经过同一平面内的A,B,C三点中的任意两点,
可以作出________条直线.
1或3
9.在右图所示的“金鱼”中,含有哪些可以用图中字母表示的线段、射线和直线?试写出来.
四、当堂练习
解:线段:线段AB,线段AC,线段BD,线段BE,线段DE,线段CD,线段CF,线段DF,线段EF;
射线:射线AB,射线AC,射线BA,射线CA;
直线:直线AB,直线AC.
10.根据要求画图:如图所示,点A,B,C,D在同一平面内.(1)过点A和点D作直线;(2)画射线CD;(3)连接AB;(4)连接BC,并反向延长BC.
四、当堂练习
解:如图所示.
11.两条直线相交,最多有1个交点.三条直线相交,最多有3个交点.四条直线相交,最多有多少个交点?
四、当堂练习
1+2=3(个)
1个
1+2+3=6(个)
1+2+3+4=10(个)
n条直线相交最多有1+2+3+...+(n-1)=????(?????????)????个交点.
?
五、课堂小结
线段、射线、直线的概念与表示
直线的性质
线段、射线、直线
线段、射线、直线的联系与区别
两点确定一条直线
六、作业布置
习题4.1
1 线段、射线、直线
第四章 基本平面图形
学习目标
1.在现实情境中理解线段、射线、直线的概念及他们的区别与联系.(重点)
2.会用不同的方法表示线段、射线、直线.(难点)
3.了解“两点确定一条直线”的几何事实.
一、导入新课
丰富的图形世界是由一些简单的图形构成的,观察下列图片,你能看到哪些平面图形?你知道它们是如何构成的吗?
一、导入新课
绷紧的琴弦,手电筒射出的光线,向两方无限延伸的笔直的铁轨等,它们可以分别抽象出哪些简单的平面图形呢?
线段、射线和直线.
二、新知探究
探究一:线段、射线、直线的概念与表示
绷紧的琴弦,黑板的边沿都可以近似地看做线段,线段有两个端点.
将线段向一个方向无限延长就形成了射线.手电筒、探照灯所射出的光线可以近似地看做射线.射线有一个端点.
将线段向两个方向无限延长就形成了直线.直线没有端点.
议一议:生活中有哪些物体可以近似地看做线段、射线、直线?
直线上两点和它们之间的部分.
直线上一点和它一旁的部分.
思考1:线段、射线、直线式如何定义的呢?
二、新知探究
思考2:怎么表示线段、射线、直线呢?
A
B
表示1: 线段 AB(或线段BA)
a
表示2:线段 a
表示:射线 OM
E
F
表示1:直线 EF(或直线FE)
表示2:直线l
M
O
l
线段的表示:用线段的两个端点字母表示,或用一个小写字母表示.
射线的表示:用端点和射线上另外一个点表示,端点必须写在前面.
直线的表示:用直线上任意两点表示,或用一个小写字母表示.
2.请分别表示出图中的线段、射线和直线。
A
B
C
1.请用两种方式分别表示图中的两条直线.
B
A
O
m
n
二、新知探究
跟踪练习
线段:线段AB、线段AC、线段BC;
射线:射线AC(或射线AB)、射线BC、射线BA、射线CA(或射线 CB);
直线:直线AB(或直线AC、直线BC).
一条直线可表示为直线AO或直线n,另一条直线可表示为直线 BO或直线m.
二、新知探究
想一想:如图所示,射线OM与射线ON表示同一条射线吗?射线MN与射线NM呢?
解:因为射线OM与射线ON端点相同,延伸方向相同,
所以射线OM与射线ON表示同一条射线.
因为射线MN与射线NM端点不同,延伸方向相反,
所以射线MN与射线NM表示不同的射线.
2.如图所示,下列说法正确的是( )
A.直线AB和直线CD是不同的直线
B.射线AB和射线BA是同一条射线
C.线段AB和线段BA是同一条线段
D.以上说法均不正确
1.下列图形中表示射线AB的是( )
二、新知探究
跟踪练习
B
C
做一做:如图,已知平面上三点A、B、C.
(1)画线段AB;
(2)画直线BC;
(3)画射线CA;
解:(1)、(2)、(3)题如图所示.
(4)如何由线段AB得到射线AB和直线AB呢?
(4)将线段AB向B方向延伸得到射线AB,将线段AB向两个方向延伸得到直线AB.
(5)直线AB与直线BC有一个公共点B.
(5)直线AB与直线BC有几个公共点?
二、新知探究
二、新知探究
知识归纳
线段、射线与直线区别与联系:
特性
类别
图形
端点个数
是否可以延伸
是否可以量度
表示方法
作图描述
表示方法
备注
线段
两个
不可
延伸
可以
量度
线段AB或线段BA或线段a
A,B两点无序
连接AB
射线
一个
向一个方向延伸
不可以量度
射线AB
A,B两点有序,端点在前
以A为端点作射线AB
直线
无
向两个方向延伸
不可以量度
直线AB或直线
BA或直线a
A,B两点无序
过A,B两点作直线AB
二、新知探究
议一议:(1)图中共有几条线段?说明你分析这个问题的具体思路;
以A为端点的线段有AB,AC,AD,AE,共4条,以B为端点且与前面不重复的线段有BC,BD,BE,共3条,以C为端点且与前面不重复的线段有CD,CE,共2条,以D为端点且与前面不重复的线段有DE,共1条,从而共有4+3+2+1=10(条)线段.
1.当直线a上有1个点时,可得到 条射线, 条线段;
2.当直线a上有2个点时,可得到 条射线, 条线段;
3.当直线a上有3个点时,可得到 条射线, 条线段;
4.当直线a上有4个点时,可得到 条射线, 条线段;
5.当直线a上有5个点时,可得到 条射线, 条线段;
6.当直线a上有6个点时,可得到 条射线, 条线段;
议一议:(2)当直线a上有n个点时,可得到 条射线, 条线段.
·
B
·
·
A
O
a
·
C
二、新知探究
2
0
4
1
6
3
8
6
2n
n(n-1)
2
10
10
12
15
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
直线上有n个点时,有线段1+2+3+...+(n-1)=????(?????????)????(条).
?
二、新知探究
指出下图中线段、射线、直线分别有多少条?并把线段表示出来.
解:线段有3条,分别为线段AB、线段AC、线段BC.
射线有6条.
直线有1条.
自己尝试把6条射线画出来
跟踪练习
(2) 过两点A、B可以画几条直线?
A
B
做一做:(1) 过一点 O 可以画几条直线?
O
二、新知探究
探究二:直线的性质
过一点可以画无数条直线。
过两点可以画一条直线。
二、新知探究
(3)如果你想将一根细木条固定在墙上,至少需要几个钉子?这样做的依据是什么吗?
至少需要2个.
根据生活经验,我们发现:经过两点有且只有一条直线.
二、新知探究
直线的性质:
经过两点有且只有________条直线.
这一事实可以简述为:__________________.
一
两点确定一条直线
知识归纳
二、新知探究
下列现象:①农民伯伯拉绳插秧;②解放军叔叔打靶瞄准;③学生早操队列对齐;④在墙上至少要用两根钉子才能把木条固定;⑤改直弯曲的河道,缩短航程.其中可以用“两点确定一条直线”来解释的有__________.(填序号)
①②③④
跟踪练习
三、典例精析
解:(1)数轴可以看作规定了原点、正方向、单位长度的直线;
(2)数轴上原点及原点右边的部分是射线,这个图形表示成射线OB或射线OC;
(3)射线OB与射线OC是同一条射线,端点表示数0;
(4)射线AB 和射线BA是两条不同的射线,它们的端点不同,射线AB的端点是点A,射线BA的端点是点B;
(5)数轴上表示绝对值不大于2的部分是从表示 -2 的点到表示+2的点C的一条线段,可以表示为线段AC.
例1:如图,数轴上点O表示原点,点A 表示-2,点B表示1,点C表示2.
(1)数轴可以看作什么图形?
(2)数轴上原点及原点右边的部分是什么图形?这个图形怎样表示?
(3)射线OB 与射线OC是同一条射线吗?端点表示什么数?
(4)射线AB与射线BA是同一条射线吗?为什么?
5)数轴上表示绝对值不大于2的部分是什么图形?这个图形怎样表示?
三、典例精析
例2:小明发现,甲乙两地的火车路线上共有 10 个站,且任意两站之间的票价都不相同.请你帮他解决列问题:
(1)有多少种不同的票价?
(2)要准备多少种不同的车票?
(2)有多少种车票是要考虑顺序的,则有 45×2=90(种).
答:要准备 90种不同的车票.
解:(1)此题目相当于一条线段上有 10个点,有多少种不同的票价即有多少条线段.故不同的票价共有=????????×????????=45(种).
答:有45 种不同的票价.
?
2.如图所示,下列几何语句不正确的是( )
A.直线AB与直线BA是同一条直线 B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线 D.线段AB与线段BA是同一条线段
四、当堂练习
1.手电筒发射出来的光线,给我们的感觉是( )
A.线段 B.射线 C.直线 D.折线
B
C
3.图中直线AB,射线CD,线段MN能够相交的是( )
4.下列说法中,错误的是( )
A.经过一点的直线可以有无数条 B.经过两点的直线只有一条
C.一条直线只能用一个字母表示 D.线段EF与线段FE是同一条线段
C
四、当堂练习
D
5.如图所示,图中的直线可以表示为 或 .
7.如图所示,其中线段有_____条,射线有____条.
四、当堂练习
直线AB(或直线BA)
直线m
6.新学期开学整理教室时,老师总是先把每一列最前面和最后面的课桌摆好,然后依次摆中间的课桌,一会儿一列课桌就整齐地摆在一条直线上了,这是因为__________________.
两点确定一条直线
3
8
8.经过同一平面内的A,B,C三点中的任意两点,
可以作出________条直线.
1或3
9.在右图所示的“金鱼”中,含有哪些可以用图中字母表示的线段、射线和直线?试写出来.
四、当堂练习
解:线段:线段AB,线段AC,线段BD,线段BE,线段DE,线段CD,线段CF,线段DF,线段EF;
射线:射线AB,射线AC,射线BA,射线CA;
直线:直线AB,直线AC.
10.根据要求画图:如图所示,点A,B,C,D在同一平面内.(1)过点A和点D作直线;(2)画射线CD;(3)连接AB;(4)连接BC,并反向延长BC.
四、当堂练习
解:如图所示.
11.两条直线相交,最多有1个交点.三条直线相交,最多有3个交点.四条直线相交,最多有多少个交点?
四、当堂练习
1+2=3(个)
1个
1+2+3=6(个)
1+2+3+4=10(个)
n条直线相交最多有1+2+3+...+(n-1)=????(?????????)????个交点.
?
五、课堂小结
线段、射线、直线的概念与表示
直线的性质
线段、射线、直线
线段、射线、直线的联系与区别
两点确定一条直线
六、作业布置
习题4.1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
