3.2 平行线分线段成比例 课件(共27张PPT)
文档属性
| 名称 | 3.2 平行线分线段成比例 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
第三章 图形的相似
3.2 平行线分线段成比例
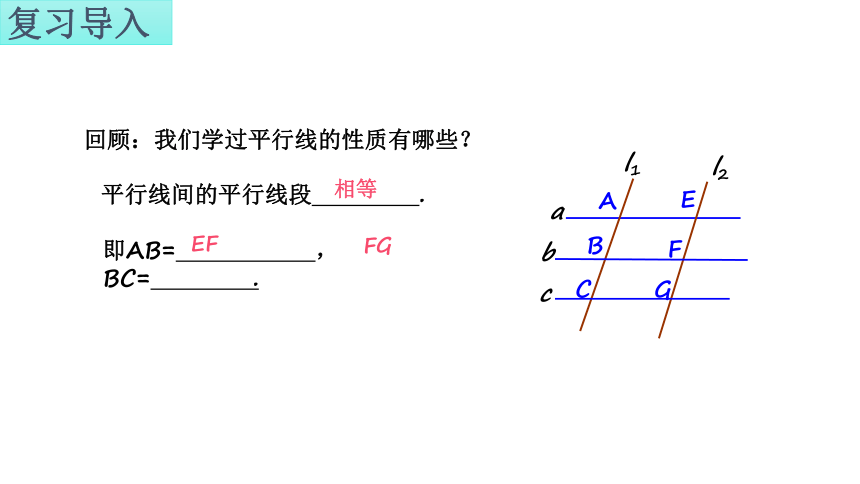
复习导入
回顾:我们学过平行线的性质有哪些?
平行线间的平行线段 .
F
E
B
A
l2
l1
a
b
c
C
G
相等
即AB= ,BC= .
EF
FG
探究新知
下图是一架梯子的示意图. AA1,BB1,CC1,DD1互相平行,若AB=BC,你能得出什么猜想?
A1B1=B1C1
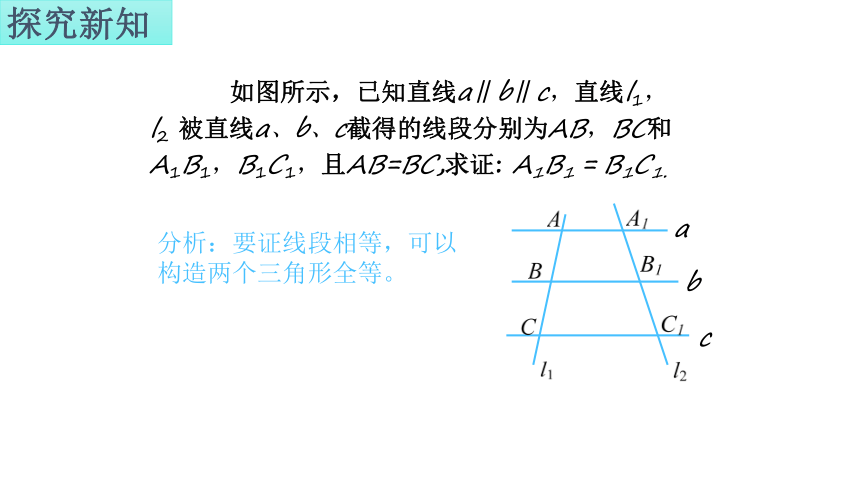
探究新知
如图所示,已知直线a∥b∥c,直线l1,l2 被直线a、b、c截得的线段分别为AB,BC和A1B1,B1C1,且AB=BC,求证: A1B1 = B1C1.
a
b
c
分析:要证线段相等,可以构造两个三角形全等。
探究新知
a
b
c
(夹在两平行线间的平行线段相等)
∴ A2B =A1B1,
在△BAA2和△BCC2中,
∴ △BAA2≌△BCC2 .
∴ BA2= BC2,
∴ A1B1 = B1C1.
过点B作直线l3∥l2 ,分别与直线a、c相交于点A2、C2.
∵ a∥b∥c,l3∥l2,
∠ABA2=∠CBC2,
BA=BC,
∠BAA2=∠BCC2,
BC2 = B1C1 .
知识要点
结论:两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
a
b
c
∵
a∥b∥c ,AB=BC ,
∴
A1B1 = B1C1 .
符号语言:
平行线等分线段定理
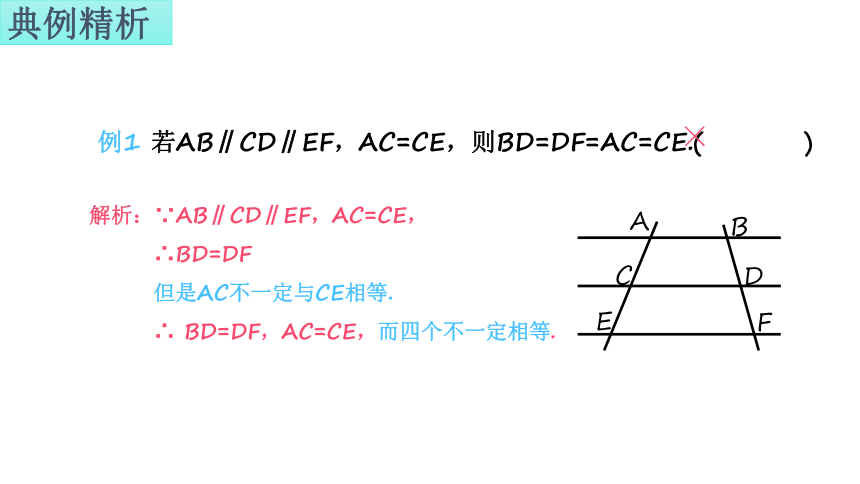
例1 若AB∥CD∥EF,AC=CE,则BD=DF=AC=CE.( )
×
A
B
C
D
E
F
解析:∵AB∥CD∥EF,AC=CE,
∴BD=DF
但是AC不一定与CE相等.
∴ BD=DF,AC=CE,而四个不一定相等.
典例精析
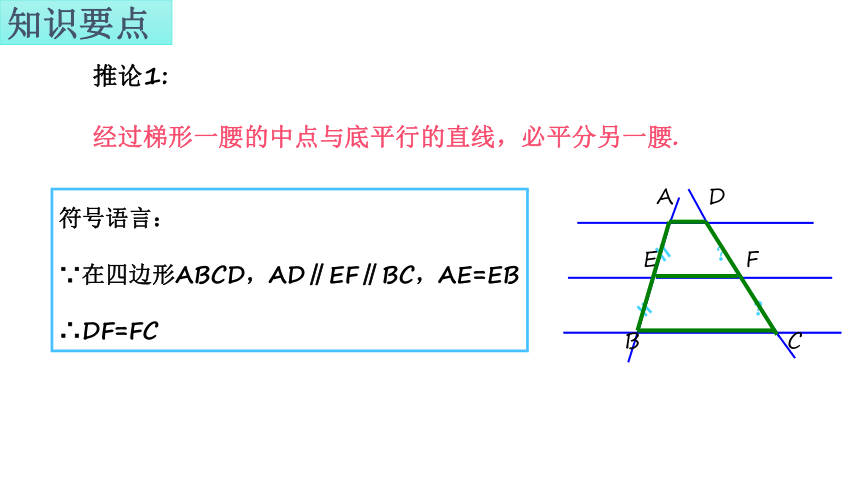
知识要点
经过梯形一腰的中点与底平行的直线,必平分另一腰.
?
?
A
B
C
D
E
F
符号语言:
∵在四边形ABCD,AD∥EF∥BC,AE=EB
∴DF=FC
推论1:
A
E
B
C
F
经过三角形一边的中点与另一边平行的直线,必平分第三边。
符号语言
∵△ABC中,EF∥BC,AE=EB
∴AF=FC
推论2:
知识要点
如图所示,已知直线 a∥b∥c,直线l1,l2 被直线a、b、c截得的线段分别为AB,BC和A1B1,B1C1,若AB= BC,则 吗?
a
b
c
=1
相等
探究新知
探究新知
a
b
c
度量AB,BC,A1B1,B1C1
还相等吗?
任意平移直线c,
1.06cm
1.59cm
1.10cm
1.65cm
=
.
∴
∵
若
a
b
c
d
e
f
因此AD=DB=BE=EF=FC .
由于a // d// b // e// f// c,
因此A1D1=D1B1=B1E1=E1F1=F1C1.
从而
则把线段AB二等分,分点为D ,过点D作直线d∥a,
把线段BC三等分,三等分点为E,F,分别过点E,
交l2于点D1 ,
F作直线e∥a,f∥a,分别交l2于点E1,F1
探究新知
类似地,我们可以证明若 则 .
类似地,进一步可证明若 .
,
,
我们还可以得到:
=
因此
探究新知
两条直线被一组平行线所截,所得的对应线段成比例.
由此,得到以下基本事实:
我们把以上基本事实简称为平行线分线段成比例.
∵
∴
a∥b∥c ,
…
符号语言:
a
b
c
平行线分线段成比例
知识要点
知识要点
典例精析
例3 如图,已知AA1//BB1//CC1,AB=2,BC=3,A1B1=1.5, 求B1C1的长.
解:∵ AA1//BB1//CC1
∴ ,
即
∴=2.25
平行线分线段成比例定理与平行线等分线段定理有何联系?
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
当1
当1
探究新知
探究新知
如图,在△ABC 中,已知DE∥BC,则和成立吗?为什么?
如图,过点A作直线MN,使MN∥DE.
∵ DE∥BC,
∴ MN∥DE∥BC.
因此AB,AC被一组平行线MN,DE,BC 所截,则由平行线分线段成比例可知, , .
同时还可以得到:.
探究新知
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
由此得到以下结论:
∵
∴
DE∥BC ,
…
符号语言:
知识要点
知识要点
若DE∥BC
则
D
E
A
B
C
…
平行于三角形一边的直线截其他两边的延长线,所得的对应线段成比例.
知识要点
例4 如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC. 若AB =3,AD = 2,EC =1.8,求AC 的长.
左上
左全
右上
右全
分析:
,
把 AE=AC-EC代入即可求解.
典例精析
∴ .
解:
∵
又 AE=AC-EC,
∴ ,
∴ 2AC=3(AC-1.8),
解得 AC=5.4.
DE ∥ BC,
2
1.8
3
典例精析
当堂练习
1.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,,EF=9,求DF的长.
解:∵ AD∥BE∥CF
∴
∴=
∴DE=6
∴DF=DE+EF=6+9=15.
2.如图,△ABC中,DE//BC,EF//AB,试判断成立吗?若成立说明理由.
解:成立,理由如下:
∵ DE∥BC,∴
∵EF//AB,∴
∴=.
当堂练习
课堂小结
平行线分线段成比例
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
两条直线被一组平行线所截,所得的对应线段成比例.
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
第三章 图形的相似
3.2 平行线分线段成比例
复习导入
回顾:我们学过平行线的性质有哪些?
平行线间的平行线段 .
F
E
B
A
l2
l1
a
b
c
C
G
相等
即AB= ,BC= .
EF
FG
探究新知
下图是一架梯子的示意图. AA1,BB1,CC1,DD1互相平行,若AB=BC,你能得出什么猜想?
A1B1=B1C1
探究新知
如图所示,已知直线a∥b∥c,直线l1,l2 被直线a、b、c截得的线段分别为AB,BC和A1B1,B1C1,且AB=BC,求证: A1B1 = B1C1.
a
b
c
分析:要证线段相等,可以构造两个三角形全等。
探究新知
a
b
c
(夹在两平行线间的平行线段相等)
∴ A2B =A1B1,
在△BAA2和△BCC2中,
∴ △BAA2≌△BCC2 .
∴ BA2= BC2,
∴ A1B1 = B1C1.
过点B作直线l3∥l2 ,分别与直线a、c相交于点A2、C2.
∵ a∥b∥c,l3∥l2,
∠ABA2=∠CBC2,
BA=BC,
∠BAA2=∠BCC2,
BC2 = B1C1 .
知识要点
结论:两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
a
b
c
∵
a∥b∥c ,AB=BC ,
∴
A1B1 = B1C1 .
符号语言:
平行线等分线段定理
例1 若AB∥CD∥EF,AC=CE,则BD=DF=AC=CE.( )
×
A
B
C
D
E
F
解析:∵AB∥CD∥EF,AC=CE,
∴BD=DF
但是AC不一定与CE相等.
∴ BD=DF,AC=CE,而四个不一定相等.
典例精析
知识要点
经过梯形一腰的中点与底平行的直线,必平分另一腰.
?
?
A
B
C
D
E
F
符号语言:
∵在四边形ABCD,AD∥EF∥BC,AE=EB
∴DF=FC
推论1:
A
E
B
C
F
经过三角形一边的中点与另一边平行的直线,必平分第三边。
符号语言
∵△ABC中,EF∥BC,AE=EB
∴AF=FC
推论2:
知识要点
如图所示,已知直线 a∥b∥c,直线l1,l2 被直线a、b、c截得的线段分别为AB,BC和A1B1,B1C1,若AB= BC,则 吗?
a
b
c
=1
相等
探究新知
探究新知
a
b
c
度量AB,BC,A1B1,B1C1
还相等吗?
任意平移直线c,
1.06cm
1.59cm
1.10cm
1.65cm
=
.
∴
∵
若
a
b
c
d
e
f
因此AD=DB=BE=EF=FC .
由于a // d// b // e// f// c,
因此A1D1=D1B1=B1E1=E1F1=F1C1.
从而
则把线段AB二等分,分点为D ,过点D作直线d∥a,
把线段BC三等分,三等分点为E,F,分别过点E,
交l2于点D1 ,
F作直线e∥a,f∥a,分别交l2于点E1,F1
探究新知
类似地,我们可以证明若 则 .
类似地,进一步可证明若 .
,
,
我们还可以得到:
=
因此
探究新知
两条直线被一组平行线所截,所得的对应线段成比例.
由此,得到以下基本事实:
我们把以上基本事实简称为平行线分线段成比例.
∵
∴
a∥b∥c ,
…
符号语言:
a
b
c
平行线分线段成比例
知识要点
知识要点
典例精析
例3 如图,已知AA1//BB1//CC1,AB=2,BC=3,A1B1=1.5, 求B1C1的长.
解:∵ AA1//BB1//CC1
∴ ,
即
∴=2.25
平行线分线段成比例定理与平行线等分线段定理有何联系?
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
当1
当1
探究新知
探究新知
如图,在△ABC 中,已知DE∥BC,则和成立吗?为什么?
如图,过点A作直线MN,使MN∥DE.
∵ DE∥BC,
∴ MN∥DE∥BC.
因此AB,AC被一组平行线MN,DE,BC 所截,则由平行线分线段成比例可知, , .
同时还可以得到:.
探究新知
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
由此得到以下结论:
∵
∴
DE∥BC ,
…
符号语言:
知识要点
知识要点
若DE∥BC
则
D
E
A
B
C
…
平行于三角形一边的直线截其他两边的延长线,所得的对应线段成比例.
知识要点
例4 如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC. 若AB =3,AD = 2,EC =1.8,求AC 的长.
左上
左全
右上
右全
分析:
,
把 AE=AC-EC代入即可求解.
典例精析
∴ .
解:
∵
又 AE=AC-EC,
∴ ,
∴ 2AC=3(AC-1.8),
解得 AC=5.4.
DE ∥ BC,
2
1.8
3
典例精析
当堂练习
1.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,,EF=9,求DF的长.
解:∵ AD∥BE∥CF
∴
∴=
∴DE=6
∴DF=DE+EF=6+9=15.
2.如图,△ABC中,DE//BC,EF//AB,试判断成立吗?若成立说明理由.
解:成立,理由如下:
∵ DE∥BC,∴
∵EF//AB,∴
∴=.
当堂练习
课堂小结
平行线分线段成比例
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
两条直线被一组平行线所截,所得的对应线段成比例.
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
