第24章 圆 期中复习 课件 (共69张PPT)
文档属性
| 名称 | 第24章 圆 期中复习 课件 (共69张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 17:39:20 | ||
图片预览




文档简介
(共69张PPT)
人教版九年级上册
【十二大考点串讲+素养提升】
第24章 圆
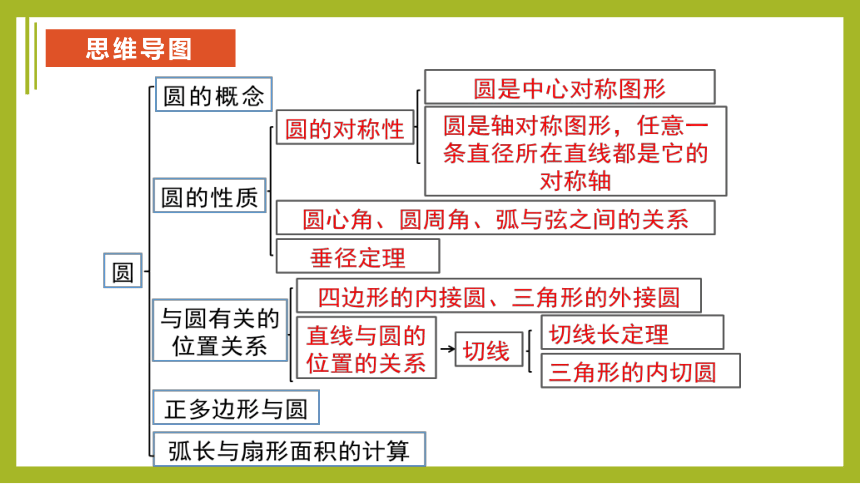
思维导图
考点一、与圆有关的概念
1.圆:平面内到定点的距离等于定长的所有点组成的图形.
2.弦:连接圆上任意两点的线段(如图中的AC)叫做弦.
·
C
O
A
B
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
劣弧与优弧
·
C
O
A
B
半圆
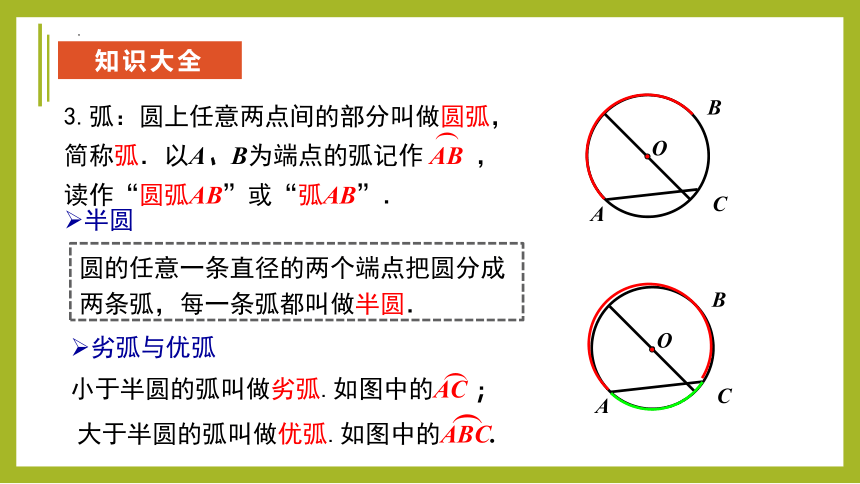
3.弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
4.等圆:能够重合的两个圆叫做等圆,容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等.
5.等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
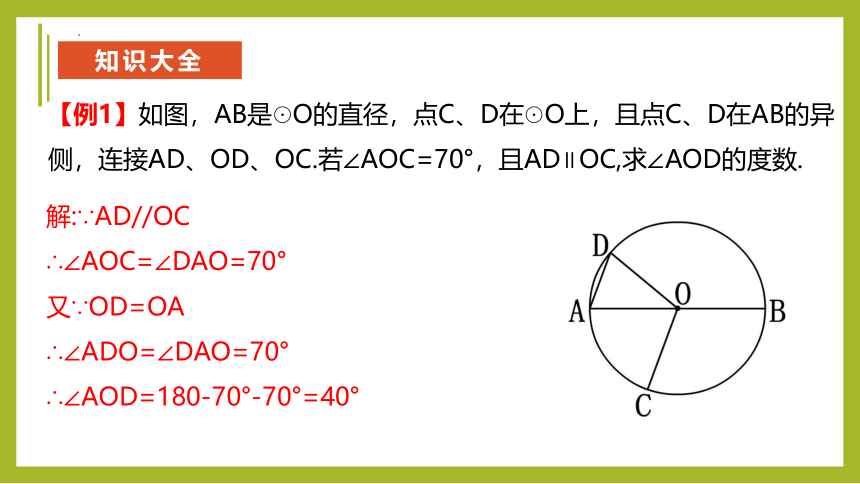
【例1】如图,AB是☉O的直径,点C、D在☉O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,求∠AOD的度数.
解:∵AD//OC
∴∠AOC=∠DAO=70°
又∵OD=OA
∴∠ADO=∠DAO=70°
∴∠AOD=180-70°-70°=40°
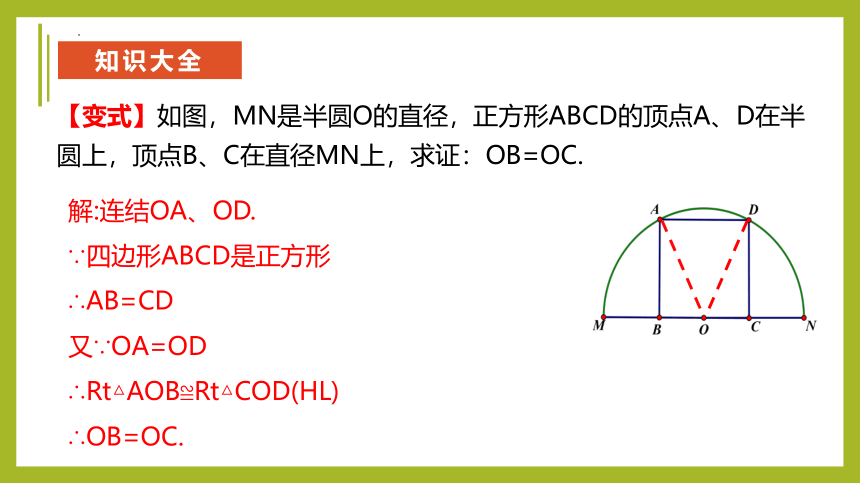
【变式】如图,MN是半圆O的直径,正方形ABCD的顶点A、D在半圆上,顶点B、C在直径MN上,求证:OB=OC.
解:连结OA、OD.
∵四边形ABCD是正方形
∴AB=CD
又∵OA=OD
∴Rt△AOB≌Rt△COD(HL)
∴OB=OC.
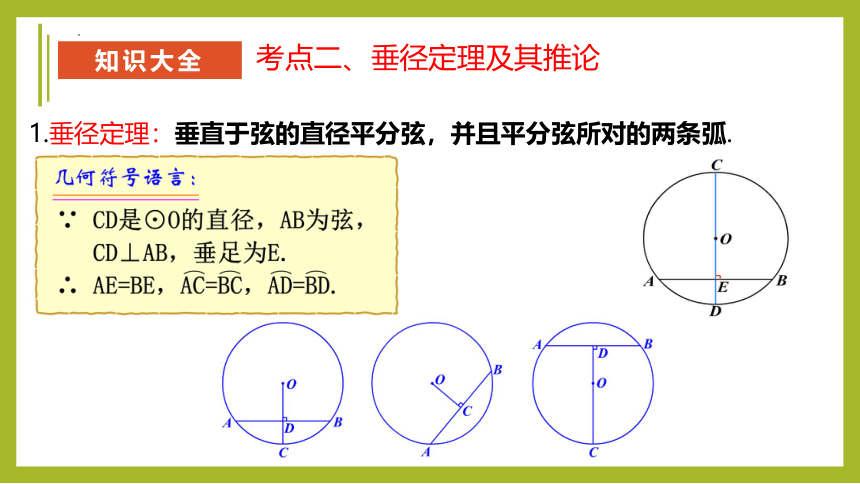
1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
考点二、垂径定理及其推论
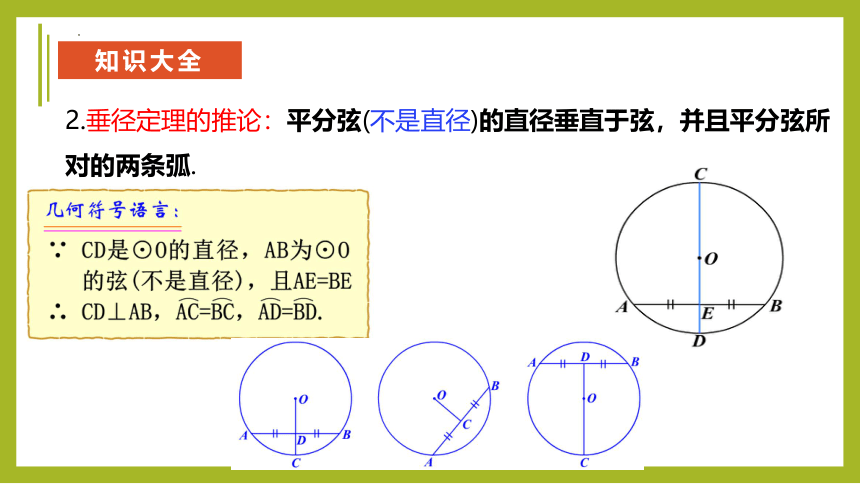
2.垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
3.涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
4.弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
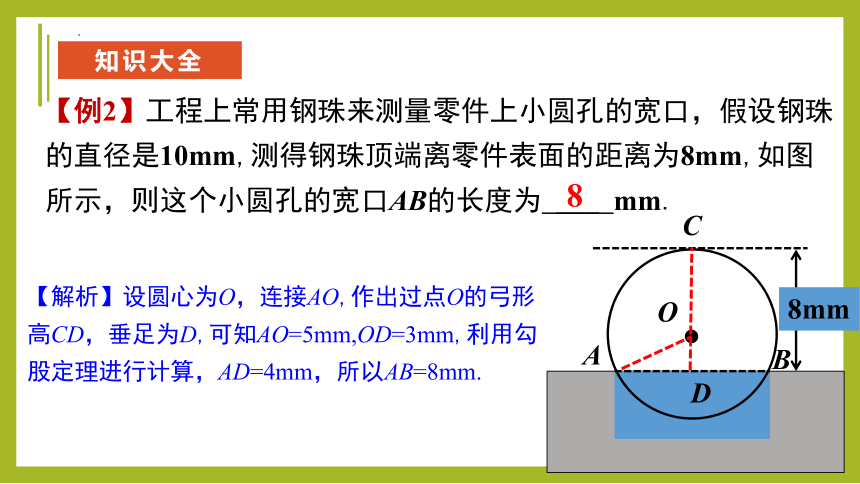
【例2】工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 ___ mm.
8
【解析】设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可知AO=5mm,OD=3mm,利用勾股定理进行计算,AD=4mm,所以AB=8mm.
8mm
A
B
C
D
O
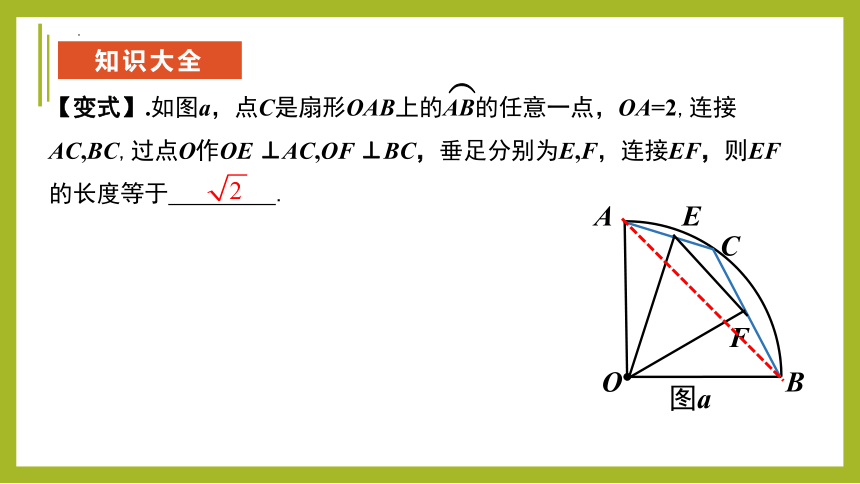
【变式】.如图a,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE ⊥AC,OF ⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
(
A
O
B
C
E
F
图a
1.圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
3.圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
2.圆心角∠AOB所对的弧为AB.
⌒
考点三、圆心角及相关概念
【例3】如图,AB,CD是⊙O的直径, ,若∠AOE=32°,则∠COE的度数是( )
A.32° B.60° C.68° D.64°
D
同样,还可以得到:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的、弦也相等.
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
考点四、圆心角、弧、弦之间的关系
【例4】如图,在☉O中,已知∠AOB=90°,C,D将 三等分,弦AB与半径0C,OD分别交于点E,F.求证:AE=CD=BF.
证明:连接AC,BD
∵C,D将弧AB三等分,
∴AC=CD=BD
∵∠AOB=90°,且OA=OB
∴∠AOC=∠COD=∠BOD=30°∠OAB=∠OBA=45°
∴∠AEC=∠AOC+∠OAB=45°+30°=75°
∵OA=OC, ∠AOC=30°,
∴∠ACO=×(180-30°)=75°
∴∠AEC=∠ACE,∴AE=AC 同理可得BF=BD,∴AE=CD=BF
【变式】如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么____________,_______.
(2)如果 ,那么____________,_______.
(3)如果∠AOB=∠COD,那么_______,_______.
(4)如果AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,
OE与OF相等吗?为什么?
解:OE=OF.理由如下:
∵ OE⊥AB,OF⊥CD,
∴ AE=AB,CF=CD
又∵ AB=CD,
∠AOB=∠COD
∠AOB=∠COD
AB=CD
AB=CD
∴ AE=CF
又∵ AO=CO,
∴ Rt△AOE≌Rt△COF(HL)
∴ OE=OF
考点五、圆周角及其定理、推论
(两个条件必须同时具备,缺一不可)
1.概念:在圆中,除圆心角外,还有一类角(如图中的∠ACB),它的顶点在圆上,并且两边都与圆相交,我们把这样的角叫做圆周角.
2.圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
3.推论1:同弧或等弧所对的圆周角相等.
4.推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
5.圆内接四边形的性质:圆内接四边形的对角互补.
【例5】在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
B
135°
【变式】如图a,四边形ABCD为☉O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是 .
点P在圆外 d>r;
点P在圆上 d=r;
点P在圆内 d<r.
不在同一直线上的三个点确定一个圆.
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
设⊙O的半径为r,点P到圆心的距离OP=d,
考点六、点与圆的位置关系
【例6】 ☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )
A.点A在☉O内部 B.点A在☉O上
C.点A在☉O外部 D.点A不在☉O上
【解析】此题需先计算出一元二次方程x2-6x+8=0的两个根,然后再根据R与d的之间的关系判断出点A与 ☉O的关系.
D
【变式】.已知⊙O的半径为4 cm,A为线段OP的中点,
当OP=7 cm时,点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上
C.点A在⊙O外 D.不能确定
A
考点七、直线与圆的位置关系
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
交点个数 位置关系 数量关系
相交
两个公共点
只有一个公共点
没有公共点
d<r
相切
相离
d=r
d>r
【例7】平面直角坐标系中,M点坐标为(-2,3),以2为半径画⊙M,则以下结论正确的是( )
A.⊙M与x轴相交,与y轴相切
B.⊙M与x轴相切,与y轴相离
C.⊙M与x轴相离,与y轴相交
D.⊙M与x轴相离,与y轴相切
D
【变式】 如图,直线AB,CD相交于点O, ∠AOD=30 °,半径为1cm的☉P的圆心在射线OA上,且与点O的距离为6cm,如果☉P以1cm/s的速度沿由A向B的方向移动,那么 秒钟后☉P与直线CD相切.
4或8
【解析】根本题应分为两种情况:(1)☉P在直线AB下面与直线CD相切;(2)☉P在直线AB上面与直线CD相切.
A
B
D
C
P
P2
P1
E
1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
考点八、切线的性质和判定
2.切线的性质定理:圆的切线垂直于过切点的半径.
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
【例8】如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M.
求证:CD与☉O相切;
(1)证明:过点O作ON⊥CD于N.连接OM
∵BC与☉O相切于点M,
∴ ∠OMC=90 °,
∵四边形ABCD是正方形,点O在AC上.
∴AC是∠BCD的角平分线,
∴ON=OM,∴ CD与☉O相切.
A
B
C
D
O
M
N
【变式】如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB延长线相交于点P.若∠COB=2∠PCB,求证:PC是⊙O的切线.
证明:如图,连接AC.
∵OA=OC,∴∠A=∠ACO.
∴∠COB=2∠ACO.
又∵∠COB=2∠PCB,∴∠ACO=∠PCB.
∵AB是⊙O的直径,∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,即OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线.
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点.
考点九、切线长定理和三角形的内切圆
1.如图,过圆外一点P有两条直线PA,PB分别与⊙O相切.经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长.
2.切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
3.三角形的内切圆
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
【例9】如图,⊙O与△ABC的边BC相切于点D,与AB、AC的延长线分别相切于点E、F,连接OB,OC.
(1)若∠ABC=80°,∠ACB=40°,求∠BOC的度数.
(2)∠BOC与∠A有怎样的数量关系,并说明理由.
解:如图,连接OD,OE,OF,则由切线的性质可知,
∠BEO=∠BDO=∠CDO=∠CFO=90°,
又∵OD=OE=OF,OB=OB,OC=OC,
∴Rt△ODB≌Rt△OEB(HL) , Rt△ODC≌Rt△OFC(HL),
∴∠EOB=∠DOB ,∠COD=∠COF,
【例9】如图,⊙O与△ABC的边BC相切于点D,与AB、AC的延长线分别相切于点E、F,连接OB,OC.
(1)若∠ABC=80°,∠ACB=40°,求∠BOC的度数.
(2)∠BOC与∠A有怎样的数量关系,并说明理由.
在△ABC中,∠A=180°-∠ABC-∠ACB=60°,
在四边形AEOF中,∠A+∠EOF=180°,
∴∠EOF=120°,
∴∠BOC=∠BOD+∠COD=∠EOF=60°.
【变式】如图,中,,是的内切圆,D,E,F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果,,求内切圆的半径.
(1)证明:∵BC,AC分别切于点D,E,∴,,
又∵,
∴四边形ODCE是矩形,
又∵,
∴矩形ODCE是正方形.
【变式】如图,中,,是的内切圆,D,E,F是切点.
(2)如果,,求内切圆的半径.
(2)解:设的半径为r,∵四边形ODCE是正方形,
∴,
在中,,
∴,,
∵与各边相切于点D,E,F,
∴,,
又∵,∴,解得
∴内切圆的半径是1.
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心,
外接圆的半径叫做正多边形的半径,
正多边形每一边所对的圆心角叫做正多边形的中心角,
中心到正多边形的一边的距离叫做正多边形的边心距.
如图,点O是正六边形ABCDEF的中心;OD是正六边形ABCDEF的半径;∠AOF是正六边形ABCDEF的中心角;OG是正六边形ABCDEF的边心距.
考点十、正多边形和圆
1.正n边形的每一个内角的度数__________.
3.正n边形的中心角__________.
2.正n边形的每一个外角的度数__________.
4.正n边形的边长a,半径R,边心距r之间有什么关系?
5.边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
【例10】如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.
求正方形EFGH的面积;
解:⑴∵正六边形的边长与其半径相等,
∴EF=OF=5.
∵四边形EFGH是正方形,
∴FG=EF=5,
∴正方形EFGH的面积是25.
【变式】如图,正五边形ABCDE内接于☉O,过点A作☉O的切线交对角线DB的延长线于点F.求证:(1)AE∥BF;(2)AB=BF.
证明:(1)∵五边形ABCDE是正五边形
∴∠BAE=∠ABC=∠C=∠EDC=∠E==108°
BC=CD
∴∠CBD=∠CDB=×(180°-∠C)=36°
∴∠ABD=∠ABC-∠CBD=108°-36°=72°
∴∠BAE+∠ABD=108°+72°=180°
∴AE∥BF
【变式】如图,正五边形ABCDE内接于☉O,过点A作☉O的切线交对角线DB的延长线于点F.求证:(1)AE∥BF;(2)AB=BF.
证明:(2)连接0A、OB.∵五边形ABCDE是正五边形,
∴∠AOB==72°
∵OA=OB
∴∠0AB=∠0BA=×(180°-72°)=54°
∵FA切☉0于A.
∴∠OAF=90°
∴∠FAB=90°-54°=36°
∵∠ABD=72°
∴∠F=72°-36°=36°=∠FAB
∴AB=BF
考点十一、弧长和扇形面积
1.弧长公式:半径为R的圆中,n°圆心角所对的弧长l
2.扇形面积公式:半径为R,圆心角为n°的扇形面积S
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
【例11】如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上,OA=1,∠AOC=120°,∠1=∠2,求扇形OEF的面积.
解:∵四边形OABC为菱形,
∴OC=OA=1.
∵ ∠AOC=120°,∠1=∠2,
∴ ∠FOE=120°.
又∵点C在以点O为圆心的圆,
【变式1】如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______.
【变式2】如图,在Rt△ABC中,∠ABC=90°,∠CAB=30°,BC=2,以AB的中点为圆心,OA的长为半径作圆交AC于点D,则图中阴影部分的面积为
_________.
【变式3】(日照中考)如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( )
A.13π cm B.14π cm C.15π cm D.16π cm
B
圆锥是由一个底面和一个侧面围成的几何体,它的底面是一个圆面,它的侧面是一个曲面.
我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线,连接圆锥顶点和底面圆心的线段叫做圆锥的高.
母线有无数条,且都相等.
圆锥的底面半径、高、母线长三者之间的关系:
考点十二、圆锥的侧面积和全面积
如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形. 设圆圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为___,扇形的弧长为_____,因此圆锥的侧面积为_____,圆锥的全面积为___________.
l
2πr
πr2+πrl
πrl
【例12】如图,从一块半径为2m的圆形铁皮上剪出一个圆周角为120°的扇形ABC,其中点O在弧BC上.(1)求被剪掉阴影部分的面积;
(2)用所得的扇形铁皮围成一个圆锥,该圆锥底面的半径是多少
解:(1)S阴影=S☉O-S扇形
=π×22-
=4π-
=(m2)
【例12】如图,从一块半径为2m的圆形铁皮上剪出一个圆周角为120°的扇形ABC,其中点O在弧BC上.(1)求被剪掉阴影部分的面积;
(2)用所得的扇形铁皮围成一个圆锥,该圆锥底面的半径是多少
解:(2)设圆锥底面的半径为rm,依题意得π×r×2=
解得r=
因此,该圆锥底面的半径是m.
【变式】如图,已知圆锥的底面半径为r=20cm,高h=20cm,现有一只蚂蚁从底边上一点A出发,在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离.
解:如图,将圆锥沿母线SA展开,得A点对应点A',线段AA'的长即为蚂蚁爬行的最短距离.
∵r=20cm,h=20cm,∴l=80cm
∴=2×20π,解得n=90
在Rt△AA'S中,AS=A'S=80cm
∴ AA' ==80(cm)
即蚂蚁爬行的最短距离为80cm.
解:(1)直线CE与⊙O相切,证明:连结OE,∵OA=OE,∴∠DAC=∠AEO.∵四边形ABCD是矩形,∴BC∥AD,∴∠ACB=∠DAC,又∵∠ACB=∠DCE,∴∠AEO=∠DCE.∵∠D=90°,∴∠DCE+∠DEC=90°,∴∠AEO+∠DEC=90°,∴∠OEC=180°-90°=90°,
即OE⊥EC.∵OE为半径,∴直线CE与⊙O相切
2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,求证:OA是⊙D的切线.
证明:过点D作DF⊥OA于F,
∵点D是∠AOB的平分线OC上任意一点,DE⊥OB,
∴DF=DE,
即D到直线OA的距离等于⊙D的半径DE,
∴⊙D与OA相切.
F
无切点,
作垂直,
证半径
3.如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(1)证明:连接OB.
∵PO⊥AB,∴AC=BC. ∴PA=PB.
∵PO=PO,
∴△PAO≌△PBO(SSS),
∴∠OBP=∠OAP.
∵PA是⊙O的切线,∴∠OAP=90°.
∴∠OBP=90°. ∴PB是⊙O的切线.
有交点,
连交点,
证垂直
(2)若AP=5,PE=13,求DE的长.
解:在Rt△APE中,
由勾股定理易得AE=12.
由(1)知AP=BP=5,则BE=8.
∵PB为的切线,∴∠OBE=90°.
设OB=r,则OE=12-r.
在Rt△OBE中,由勾股定理得r2+82=(12-r)2.
解得r= .
4. 已知:如图,PA,PB是⊙O的切线,A、B为切点,过 上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70°,求∠DOE的度数;
解:(1)连接OA、OB、OC,
∴∠DOE= ∠AOB.
∵⊙O分别切PA、PB、DE于点A、B、C,
∴OA⊥PA,OB⊥PB,OC⊥DE,AD=CD,BE=CE,
∴OD平分∠AOC,OE平分∠BOC.
∵∠P+∠AOB=180°,∠P=70°,
∴∠AOB=110°,∠DOE=55°.
(2)∵⊙O分别切PA、PB、DE于A、B、C,
(2)若PA=4 cm,求△PDE的周长.
∴AD=CD,BE=CE.
∴△PDE的周长=PD+PE+CD+CE
=PD+AD+BE+PE=2PA=8(cm)
5.(卧龙区模拟)如图,在△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,过点D作DE⊥AC于点E,CA的延长线交⊙O于点F,连结BF.
(1)若AF=1,AC=3,求BF的值;
(2)求证:DE为⊙O的切线.
人教版九年级上册
【十二大考点串讲+素养提升】
第24章 圆
思维导图
考点一、与圆有关的概念
1.圆:平面内到定点的距离等于定长的所有点组成的图形.
2.弦:连接圆上任意两点的线段(如图中的AC)叫做弦.
·
C
O
A
B
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
劣弧与优弧
·
C
O
A
B
半圆
3.弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
4.等圆:能够重合的两个圆叫做等圆,容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等.
5.等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
【例1】如图,AB是☉O的直径,点C、D在☉O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,求∠AOD的度数.
解:∵AD//OC
∴∠AOC=∠DAO=70°
又∵OD=OA
∴∠ADO=∠DAO=70°
∴∠AOD=180-70°-70°=40°
【变式】如图,MN是半圆O的直径,正方形ABCD的顶点A、D在半圆上,顶点B、C在直径MN上,求证:OB=OC.
解:连结OA、OD.
∵四边形ABCD是正方形
∴AB=CD
又∵OA=OD
∴Rt△AOB≌Rt△COD(HL)
∴OB=OC.
1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
考点二、垂径定理及其推论
2.垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
3.涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
4.弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
【例2】工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 ___ mm.
8
【解析】设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可知AO=5mm,OD=3mm,利用勾股定理进行计算,AD=4mm,所以AB=8mm.
8mm
A
B
C
D
O
【变式】.如图a,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE ⊥AC,OF ⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
(
A
O
B
C
E
F
图a
1.圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
3.圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
2.圆心角∠AOB所对的弧为AB.
⌒
考点三、圆心角及相关概念
【例3】如图,AB,CD是⊙O的直径, ,若∠AOE=32°,则∠COE的度数是( )
A.32° B.60° C.68° D.64°
D
同样,还可以得到:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的、弦也相等.
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
考点四、圆心角、弧、弦之间的关系
【例4】如图,在☉O中,已知∠AOB=90°,C,D将 三等分,弦AB与半径0C,OD分别交于点E,F.求证:AE=CD=BF.
证明:连接AC,BD
∵C,D将弧AB三等分,
∴AC=CD=BD
∵∠AOB=90°,且OA=OB
∴∠AOC=∠COD=∠BOD=30°∠OAB=∠OBA=45°
∴∠AEC=∠AOC+∠OAB=45°+30°=75°
∵OA=OC, ∠AOC=30°,
∴∠ACO=×(180-30°)=75°
∴∠AEC=∠ACE,∴AE=AC 同理可得BF=BD,∴AE=CD=BF
【变式】如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么____________,_______.
(2)如果 ,那么____________,_______.
(3)如果∠AOB=∠COD,那么_______,_______.
(4)如果AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,
OE与OF相等吗?为什么?
解:OE=OF.理由如下:
∵ OE⊥AB,OF⊥CD,
∴ AE=AB,CF=CD
又∵ AB=CD,
∠AOB=∠COD
∠AOB=∠COD
AB=CD
AB=CD
∴ AE=CF
又∵ AO=CO,
∴ Rt△AOE≌Rt△COF(HL)
∴ OE=OF
考点五、圆周角及其定理、推论
(两个条件必须同时具备,缺一不可)
1.概念:在圆中,除圆心角外,还有一类角(如图中的∠ACB),它的顶点在圆上,并且两边都与圆相交,我们把这样的角叫做圆周角.
2.圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
3.推论1:同弧或等弧所对的圆周角相等.
4.推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
5.圆内接四边形的性质:圆内接四边形的对角互补.
【例5】在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
B
135°
【变式】如图a,四边形ABCD为☉O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是 .
点P在圆外 d>r;
点P在圆上 d=r;
点P在圆内 d<r.
不在同一直线上的三个点确定一个圆.
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
设⊙O的半径为r,点P到圆心的距离OP=d,
考点六、点与圆的位置关系
【例6】 ☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )
A.点A在☉O内部 B.点A在☉O上
C.点A在☉O外部 D.点A不在☉O上
【解析】此题需先计算出一元二次方程x2-6x+8=0的两个根,然后再根据R与d的之间的关系判断出点A与 ☉O的关系.
D
【变式】.已知⊙O的半径为4 cm,A为线段OP的中点,
当OP=7 cm时,点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上
C.点A在⊙O外 D.不能确定
A
考点七、直线与圆的位置关系
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
交点个数 位置关系 数量关系
相交
两个公共点
只有一个公共点
没有公共点
d<r
相切
相离
d=r
d>r
【例7】平面直角坐标系中,M点坐标为(-2,3),以2为半径画⊙M,则以下结论正确的是( )
A.⊙M与x轴相交,与y轴相切
B.⊙M与x轴相切,与y轴相离
C.⊙M与x轴相离,与y轴相交
D.⊙M与x轴相离,与y轴相切
D
【变式】 如图,直线AB,CD相交于点O, ∠AOD=30 °,半径为1cm的☉P的圆心在射线OA上,且与点O的距离为6cm,如果☉P以1cm/s的速度沿由A向B的方向移动,那么 秒钟后☉P与直线CD相切.
4或8
【解析】根本题应分为两种情况:(1)☉P在直线AB下面与直线CD相切;(2)☉P在直线AB上面与直线CD相切.
A
B
D
C
P
P2
P1
E
1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
考点八、切线的性质和判定
2.切线的性质定理:圆的切线垂直于过切点的半径.
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
【例8】如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M.
求证:CD与☉O相切;
(1)证明:过点O作ON⊥CD于N.连接OM
∵BC与☉O相切于点M,
∴ ∠OMC=90 °,
∵四边形ABCD是正方形,点O在AC上.
∴AC是∠BCD的角平分线,
∴ON=OM,∴ CD与☉O相切.
A
B
C
D
O
M
N
【变式】如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB延长线相交于点P.若∠COB=2∠PCB,求证:PC是⊙O的切线.
证明:如图,连接AC.
∵OA=OC,∴∠A=∠ACO.
∴∠COB=2∠ACO.
又∵∠COB=2∠PCB,∴∠ACO=∠PCB.
∵AB是⊙O的直径,∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,即OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线.
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点.
考点九、切线长定理和三角形的内切圆
1.如图,过圆外一点P有两条直线PA,PB分别与⊙O相切.经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长.
2.切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
3.三角形的内切圆
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
【例9】如图,⊙O与△ABC的边BC相切于点D,与AB、AC的延长线分别相切于点E、F,连接OB,OC.
(1)若∠ABC=80°,∠ACB=40°,求∠BOC的度数.
(2)∠BOC与∠A有怎样的数量关系,并说明理由.
解:如图,连接OD,OE,OF,则由切线的性质可知,
∠BEO=∠BDO=∠CDO=∠CFO=90°,
又∵OD=OE=OF,OB=OB,OC=OC,
∴Rt△ODB≌Rt△OEB(HL) , Rt△ODC≌Rt△OFC(HL),
∴∠EOB=∠DOB ,∠COD=∠COF,
【例9】如图,⊙O与△ABC的边BC相切于点D,与AB、AC的延长线分别相切于点E、F,连接OB,OC.
(1)若∠ABC=80°,∠ACB=40°,求∠BOC的度数.
(2)∠BOC与∠A有怎样的数量关系,并说明理由.
在△ABC中,∠A=180°-∠ABC-∠ACB=60°,
在四边形AEOF中,∠A+∠EOF=180°,
∴∠EOF=120°,
∴∠BOC=∠BOD+∠COD=∠EOF=60°.
【变式】如图,中,,是的内切圆,D,E,F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果,,求内切圆的半径.
(1)证明:∵BC,AC分别切于点D,E,∴,,
又∵,
∴四边形ODCE是矩形,
又∵,
∴矩形ODCE是正方形.
【变式】如图,中,,是的内切圆,D,E,F是切点.
(2)如果,,求内切圆的半径.
(2)解:设的半径为r,∵四边形ODCE是正方形,
∴,
在中,,
∴,,
∵与各边相切于点D,E,F,
∴,,
又∵,∴,解得
∴内切圆的半径是1.
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心,
外接圆的半径叫做正多边形的半径,
正多边形每一边所对的圆心角叫做正多边形的中心角,
中心到正多边形的一边的距离叫做正多边形的边心距.
如图,点O是正六边形ABCDEF的中心;OD是正六边形ABCDEF的半径;∠AOF是正六边形ABCDEF的中心角;OG是正六边形ABCDEF的边心距.
考点十、正多边形和圆
1.正n边形的每一个内角的度数__________.
3.正n边形的中心角__________.
2.正n边形的每一个外角的度数__________.
4.正n边形的边长a,半径R,边心距r之间有什么关系?
5.边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
【例10】如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.
求正方形EFGH的面积;
解:⑴∵正六边形的边长与其半径相等,
∴EF=OF=5.
∵四边形EFGH是正方形,
∴FG=EF=5,
∴正方形EFGH的面积是25.
【变式】如图,正五边形ABCDE内接于☉O,过点A作☉O的切线交对角线DB的延长线于点F.求证:(1)AE∥BF;(2)AB=BF.
证明:(1)∵五边形ABCDE是正五边形
∴∠BAE=∠ABC=∠C=∠EDC=∠E==108°
BC=CD
∴∠CBD=∠CDB=×(180°-∠C)=36°
∴∠ABD=∠ABC-∠CBD=108°-36°=72°
∴∠BAE+∠ABD=108°+72°=180°
∴AE∥BF
【变式】如图,正五边形ABCDE内接于☉O,过点A作☉O的切线交对角线DB的延长线于点F.求证:(1)AE∥BF;(2)AB=BF.
证明:(2)连接0A、OB.∵五边形ABCDE是正五边形,
∴∠AOB==72°
∵OA=OB
∴∠0AB=∠0BA=×(180°-72°)=54°
∵FA切☉0于A.
∴∠OAF=90°
∴∠FAB=90°-54°=36°
∵∠ABD=72°
∴∠F=72°-36°=36°=∠FAB
∴AB=BF
考点十一、弧长和扇形面积
1.弧长公式:半径为R的圆中,n°圆心角所对的弧长l
2.扇形面积公式:半径为R,圆心角为n°的扇形面积S
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
【例11】如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上,OA=1,∠AOC=120°,∠1=∠2,求扇形OEF的面积.
解:∵四边形OABC为菱形,
∴OC=OA=1.
∵ ∠AOC=120°,∠1=∠2,
∴ ∠FOE=120°.
又∵点C在以点O为圆心的圆,
【变式1】如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______.
【变式2】如图,在Rt△ABC中,∠ABC=90°,∠CAB=30°,BC=2,以AB的中点为圆心,OA的长为半径作圆交AC于点D,则图中阴影部分的面积为
_________.
【变式3】(日照中考)如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( )
A.13π cm B.14π cm C.15π cm D.16π cm
B
圆锥是由一个底面和一个侧面围成的几何体,它的底面是一个圆面,它的侧面是一个曲面.
我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线,连接圆锥顶点和底面圆心的线段叫做圆锥的高.
母线有无数条,且都相等.
圆锥的底面半径、高、母线长三者之间的关系:
考点十二、圆锥的侧面积和全面积
如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形. 设圆圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为___,扇形的弧长为_____,因此圆锥的侧面积为_____,圆锥的全面积为___________.
l
2πr
πr2+πrl
πrl
【例12】如图,从一块半径为2m的圆形铁皮上剪出一个圆周角为120°的扇形ABC,其中点O在弧BC上.(1)求被剪掉阴影部分的面积;
(2)用所得的扇形铁皮围成一个圆锥,该圆锥底面的半径是多少
解:(1)S阴影=S☉O-S扇形
=π×22-
=4π-
=(m2)
【例12】如图,从一块半径为2m的圆形铁皮上剪出一个圆周角为120°的扇形ABC,其中点O在弧BC上.(1)求被剪掉阴影部分的面积;
(2)用所得的扇形铁皮围成一个圆锥,该圆锥底面的半径是多少
解:(2)设圆锥底面的半径为rm,依题意得π×r×2=
解得r=
因此,该圆锥底面的半径是m.
【变式】如图,已知圆锥的底面半径为r=20cm,高h=20cm,现有一只蚂蚁从底边上一点A出发,在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离.
解:如图,将圆锥沿母线SA展开,得A点对应点A',线段AA'的长即为蚂蚁爬行的最短距离.
∵r=20cm,h=20cm,∴l=80cm
∴=2×20π,解得n=90
在Rt△AA'S中,AS=A'S=80cm
∴ AA' ==80(cm)
即蚂蚁爬行的最短距离为80cm.
解:(1)直线CE与⊙O相切,证明:连结OE,∵OA=OE,∴∠DAC=∠AEO.∵四边形ABCD是矩形,∴BC∥AD,∴∠ACB=∠DAC,又∵∠ACB=∠DCE,∴∠AEO=∠DCE.∵∠D=90°,∴∠DCE+∠DEC=90°,∴∠AEO+∠DEC=90°,∴∠OEC=180°-90°=90°,
即OE⊥EC.∵OE为半径,∴直线CE与⊙O相切
2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,求证:OA是⊙D的切线.
证明:过点D作DF⊥OA于F,
∵点D是∠AOB的平分线OC上任意一点,DE⊥OB,
∴DF=DE,
即D到直线OA的距离等于⊙D的半径DE,
∴⊙D与OA相切.
F
无切点,
作垂直,
证半径
3.如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(1)证明:连接OB.
∵PO⊥AB,∴AC=BC. ∴PA=PB.
∵PO=PO,
∴△PAO≌△PBO(SSS),
∴∠OBP=∠OAP.
∵PA是⊙O的切线,∴∠OAP=90°.
∴∠OBP=90°. ∴PB是⊙O的切线.
有交点,
连交点,
证垂直
(2)若AP=5,PE=13,求DE的长.
解:在Rt△APE中,
由勾股定理易得AE=12.
由(1)知AP=BP=5,则BE=8.
∵PB为的切线,∴∠OBE=90°.
设OB=r,则OE=12-r.
在Rt△OBE中,由勾股定理得r2+82=(12-r)2.
解得r= .
4. 已知:如图,PA,PB是⊙O的切线,A、B为切点,过 上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70°,求∠DOE的度数;
解:(1)连接OA、OB、OC,
∴∠DOE= ∠AOB.
∵⊙O分别切PA、PB、DE于点A、B、C,
∴OA⊥PA,OB⊥PB,OC⊥DE,AD=CD,BE=CE,
∴OD平分∠AOC,OE平分∠BOC.
∵∠P+∠AOB=180°,∠P=70°,
∴∠AOB=110°,∠DOE=55°.
(2)∵⊙O分别切PA、PB、DE于A、B、C,
(2)若PA=4 cm,求△PDE的周长.
∴AD=CD,BE=CE.
∴△PDE的周长=PD+PE+CD+CE
=PD+AD+BE+PE=2PA=8(cm)
5.(卧龙区模拟)如图,在△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,过点D作DE⊥AC于点E,CA的延长线交⊙O于点F,连结BF.
(1)若AF=1,AC=3,求BF的值;
(2)求证:DE为⊙O的切线.
同课章节目录
