第二章 圆【考点串讲 课件】 69张ppt-2023-2024学年九年级数学上学期期中考点大串讲(苏科版)
文档属性
| 名称 | 第二章 圆【考点串讲 课件】 69张ppt-2023-2024学年九年级数学上学期期中考点大串讲(苏科版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 18:00:21 | ||
图片预览










文档简介
第二章
对称图形——圆
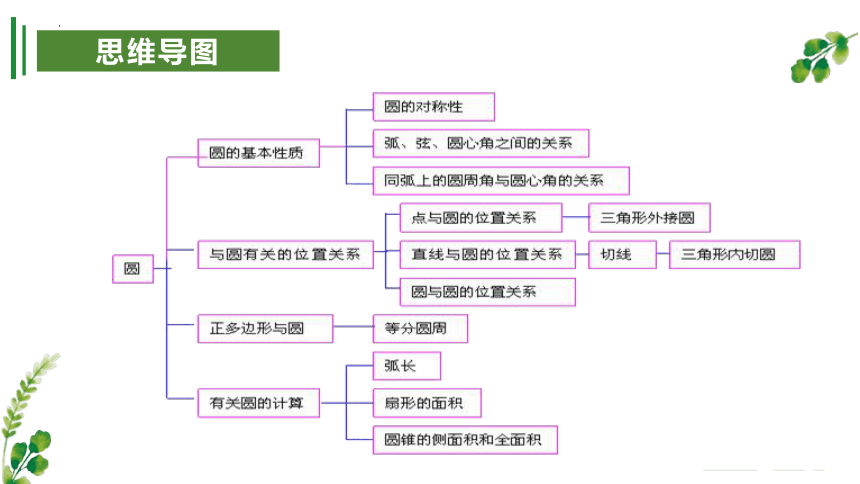
思维导图
知识大全
考点精析
常用技巧或结论
九年级期中考试复习
思维导图
知识大全
考点一 圆的相关概念
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
其中,固定的端点O叫做圆心.
线段OA叫做半径,一般用r表示.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
圆的另一定义(静态):圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形.
知识大全
考点一 圆的相关概念
经过圆心的弦(如图中的AB)叫做直径.
连接圆上任意两点的线段(如图AC)叫做弦.
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB ,读作“圆弧AB”或“弧AB”.
⌒
圆的任意一条直径的两个端点把圆分成的两条弧,每一条弧都叫做半圆.
小于半圆的弧(如图中的AB)叫做劣弧
⌒
大于半圆的弧(用三个字母表示,如图中的ACB)叫做优弧.
⌒
知识大全
考点一 圆的相关概念
圆心相同,半径不相等的两个圆叫做同心圆.
能够互相重合的两个圆叫做等圆.
O
在同圆或等圆中,能够互相重合的弧叫做等弧.
知识大全
考点一 圆的相关概念
圆的轴对称性:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
圆是中心对称图形,圆心就是它的对称中心.
圆的旋转不变性:一个圆绕圆心旋转任意角度,所得图形和原图形重合.
注意事项
考点一 圆的相关概念
一是圆心,圆心确定其位置;
二是半径,半径确定其大小.
【提问】确定一个圆的要素是什么?
1.弦和直径都是线段.
【提问】直径和弦是什么关系呢?
2.凡直径都是弦,是圆中最长的弦,但弦不一定是直径.
【提问】弧、半圆、优弧、劣弧是什么关系呢?
1.弧分为是优弧、劣弧、半圆,
2.半圆是弧,但弧不一定是半圆,
3.半圆既不是劣弧,也不是优弧.
注意事项
考点一 圆的相关概念
[结论]1)等弧的长度一定相等.
2)长度相等的弧不一定是等弧.
3)等弧仅仅存在于同圆或者等圆中.
【提问】长度相等的弧是等弧?
可见这两条弧不可能完全重合,实际上这两条弧弯曲程度不同
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
D
C
A
B
︵
︵
针对训练
考点一 圆的相关概念
例1.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有
A.4个 B.3个 C.2个 D.1个
【详解】解:①经过圆心的弦是直径,即直径是弦,弦不一定是直径,故正确;
②当三点共线的时候,不能作圆,故错误;
③三角形的外心是三角形三边的垂直平分线的交点,所以三角形的外心到三角形各顶点的距离都相等,故正确;
④在同圆或等圆中,能够互相重合的弧是等弧,所以半径相等的两个半圆是等弧,故正确.
故选:B.
针对训练
考点一 圆的相关概念
1.下列条件中,能确定一个圆的是(???????)
A.以点O为圆心 B.以10cm长为半径
C.以点A为圆心,4cm长为半径 D.经过已知点M
2 判断下列说法的正误:
1)弦是直径( )
2)直径是弦( )
3)半径是弦( )
4)直径是圆中最长的弦( )
5)过圆心的线段是直径( )
6)过圆心的直线是直径( )
?
√
√
针对训练
考点一 圆的相关概念
3.如图,请正确的方式表示出以点A为端点的优弧及劣弧.
⌒
⌒
解:优弧:ACD、ACF、ADE、ADC
劣弧:AC、AE、AF、AD
⌒
⌒
⌒
⌒
⌒
⌒
知识大全
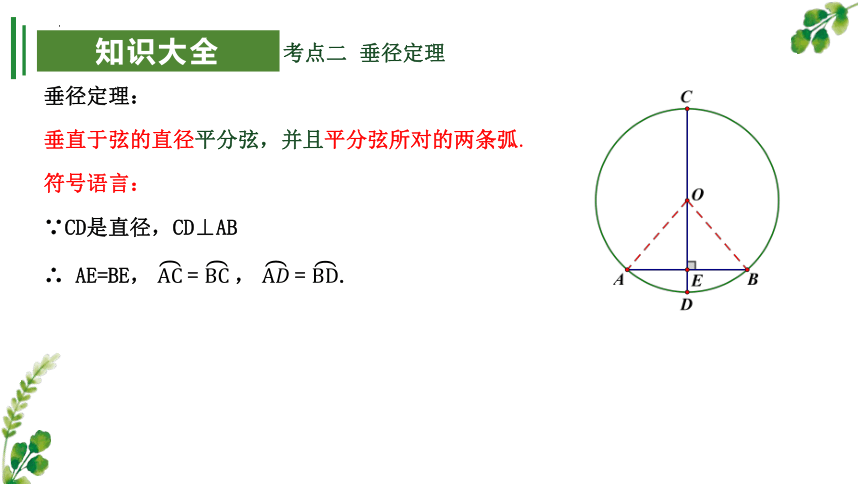
考点二 垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理:
符号语言:
∵CD是直径,CD⊥AB
∴ AE=BE, AC?= BC?, A?????= BD.
?
知识大全
考点二 垂径定理
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理推论:
符号语言:
∵CD是直径, AE=BE
∴ CD⊥AB , AC?= BC?, A?????= BD.
?
解题方法
考点二 垂径定理
垂径定理的基本图形:
垂径定理的解题思路:
弦心距:圆心到弦的距离(即圆心到弦的垂线段的距离).
在Rt△OEB中,由勾股定理得:弦心距2+半弦2=半径2
?
垂径定理的解题技巧:
见弦常作弦心距,连接半径,构造直角三角形用勾股定理求解
针对训练
考点二 垂径定理
例2 如图是一个圆弧形门拱,拱高1m ,跨度4m ,那么这个门拱的半径为( )
A.2m B.2.5m C.3m D.5m
【详解】
设这个门拱的半径为r,则OB=r?1,
∵CD=4m,AB⊥CD,
∴BC= CD=2m,
在Rt△BOC中,
∵BC2+OB2=OC2 ,即22 +(r?1) 2 =r2,解得r=2.5m.
故选B.
针对训练
考点二 垂径定理
1. 如图,在?O中,AB=8,OA=5,则OE= ,ED= .
2.如图,在?O中,OA=5,ED=2,则OE= ,AB= .
?
?
?
?
2
3
3
4
3
2
3
8
针对训练
考点二 垂径定理
3.如图,在?O中,AB=8,ED=2,则OA= ,OE= .
?
?
r - 2
r
r2 = (r - 2)2 + 42
5
3
[结论]半径、弦长、弦心距、弓形高中,知二求二.
知识大全
考点三 弧、弦、圆心角的关系
同圆和等圆中,圆心角、弧、弦之间的关系:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.
在同圆或等圆中,相等的弦所对的圆心角相等,所对优弧和劣弧分别相等.
【总结】在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
针对训练
考点三 弧、弦、圆心角的关系
·
C
A
B
D
E
F
O
例3 AB、CD是⊙O的两条弦.
1)如果AB=CD,那么 ___________,_________________.
2)如果AB=CD?,那么 ____________,_____________.
3)如果∠AOB=∠COD,那么 _____________, _____________ .
4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
?
AB=CD
?
∠AOB=∠COD
?
AB=CD
∠AOB=∠COD
?
AB=CD
AB=CD
?
∵AB=CD,∴∠AOB=∠COD.
∵AO=CO,BO=DO,则△AOB ≌ △COD.
而OE、OF是AB与CD对应边上的高,
∴OE=OF.
针对训练
考点三 弧、弦、圆心角的关系
1.如图1,AB是⊙O的直径,BC?=CD?=DE ,∠AOE=66°,则∠COD的度数是( )
A.108° B.72° C.48° D.38°
2. 如图,已知∠????????????=∠????????????,下列结论不一定成立的是( )
A.????????=???????? B.????????=????????
C.△????????????≌△???????????? D.△????????????,△????????????都是等边三角形
?
针对训练
考点三 弧、弦、圆心角的关系
3.如图,AB、CD是⊙O的两条弦,且AB=CD.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,连接OP.下列结论正确的个数是( )
①AB=CD;②OM=ON;③PA=PC;④∠BPO=∠DPO
A.1个 B.2个 C.3个 D.4个
?
【详解】解:如图连接OB、OD;∵AB=CD,∴????????=????????,故①正确
∵OM⊥AB,ON⊥CD,∴AM=MB,CN=ND,∴BM=DN,∵OB=OD∴Rt△OMB≌Rt△OND,
∴OM=ON,故②正确,
∵OP=OP,∴Rt△OPM≌Rt△OPN,∴PM=PN,∠OPB=∠OPD,故④正确,
∵AM=CN,∴PA=PC,故③正确,故选:D.
?
知识大全
考点四 圆周角定理及推论
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
圆周角定理推论:
推论1:同弧或等弧所对的圆周角相等
推论2:直径(或半圆)所对的圆周角是直角;
90°的圆周角所对的弦是直径,所对的弧是半圆.
解题方法
考点四 圆周角定理及推论
圆周角的判断方法:1)顶点在圆上;2)两边都和圆相交.
针对训练
考点四 圆周角定理及推论
例4.如图,⊙O中弦BC与半径OA相交于点D,连接AB,OC,若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25° B.27.5° C.30° D.35°
【解析】
∵∠A=60°,∠ADC=85°,
∴∠B=25°,∠CDO=95°,
∴∠AOC=2∠B=50°,
∴∠C=180°-95°-50°=35°
故选D.
针对训练
考点四 圆周角定理及推论
1.如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是( )
A.40° B.50° C.70° D.80°
2.如图,已知△ACD和△ABE都内接于同一个圆,则∠ADC+∠AEB+∠BAC=( )
A.90° B.180° C.270° D.360°
【详解】∵∠ABC=20°∴∠AOC=40°∵AB是⊙O的弦,OC⊥AB,∴∠AOC=∠BOC=40°,∴∠AOB=80°,故选:D.
【详解】∵∠ADC,∠AEB,∠BAC所对圆弧正好是一个圆周,
∴∠ADC+∠AEB+∠BAC=180°.故选B.
知识大全
考点五 圆内接四边形
圆内接多边形的概念:
如果多边形的所有顶点均在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做多边形的外接圆.
圆内接多边形的性质:
圆内接四边形的对角互补.
针对训练
考点五 圆内接四边形
例5 如图,四边形ABCD内接于⊙O,∠BOD=140°,求∠BCD的度数.
【详解】
∵∠BOD=140°,
∴∠A=12∠BOD=70°,
∴∠BCD=180°﹣∠A=110°.
?
针对训练
考点五 圆内接四边形
1.若四边形????????????????是圆内接四边形,若它的内角∠A:∠C=2:3,则∠????= .
2.如图,已知⊙O的半径为2,ΔABC内接于⊙O,∠ACB=135°,则AB= .
?
72°
?
【详解】连接AD、AE、OA、OB,
∵⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,
∴∠ADB=45°,∴∠AOB=90°,
∵OA=OB=2,∴AB=22,故答案为:22.
?
知识大全
考点六 点/直线与圆的位置关系
r
·
O
A
P
P’
P’’
d<r
d=r
d>r
点P 在⊙O内
点P’在⊙O上
点P”在⊙O外
符号“<=>?”读作“等价于”,
“A<=>B”表示由A条件可推出结论B,B结论可推出条件A.
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
知识大全
考点六 点/直线与圆的位置关系
1)直线与圆没有公共点,称为直线与圆相离.
2)直线与圆只有一个公共点,称为直线与圆相切,这条直线叫做圆的切线,这个公共点叫切点.
3)直线与圆有两个公共点,称为直线与圆相交.
这条直线叫做圆的割线.
切点
切线
割线
解题技巧
考点六 点/直线与圆的位置关系
1)判断点与圆的位置关系的实质是判断点到圆心的距离和半径的大小关系.
2)已知点到圆心的距离与半径的关系,可以确定该点与圆的位置关系,
反过来,由点与圆的位置关系也可以确定该点到圆心的距离与半径的关系.
3)圆的外部可以看成到圆心的距离大于半径的点的集合;.
圆的内部可以看成到圆心的距离小于半径的点的集合.
针对训练
考点六 点/直线与圆的位置关系
例6.已知⊙O的面积为25π:
1)若PO=5.5,则点P在 ;
2)若PO= 4 ,则点P在 ;
3)若PO= ,则点P在圆上;
4)若点P不在圆外,则PO__________.
1.设⊙O的半径为5,圆心的坐标为(0,0),点 P的坐标为(4,-3),
则点P在__________.
圆外
圆内
5
≤5
圆上
针对训练
考点六 点/直线与圆的位置关系
2.圆心为O的两个同心圆,半径分别为1和2,若OP= 3 ,则点P在( )
A.在大圆内 B.在小圆内
C.小圆外 D.大圆内,小圆外
3.在同一平面内,在⊙O外有一个定点P到圆上的距离最长为10,最短为2,则⊙O的半径是( )
A.3 B.4 C.5 D.6
?
o
针对训练
考点六 点/直线与圆的位置关系
例7 已知圆的直径为14cm,设直线和圆心的距离为d :
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
2)若d= 7cm ,则直线与圆______, 直线与圆有____个公共点.
3)若d= 8cm ,则直线与圆______, 直线与圆有____个公共点.
相交
相切
相离
2
1
0
针对训练
考点六 点/直线与圆的位置关系
1.在平面直角坐标系中,以点(﹣2,3)为圆心,半径为3的圆一定(????)
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
2.设⊙O的半径为4cm,直线L上一点A到圆心的距离为4cm,则直线L与⊙O的位置关系是______.
【详解】∵直线上一点到圆心距离为4cm,
∴圆心到直线的距离≤4cm,∴直线与圆相切或相交.
故答案为:相切或相交
针对训练
考点六 点/直线与圆的位置关系
3.在Rt△ABC中,∠C=90°,∠B=30°,O是AB上的一点,OA=m,⊙O的半径为r,当r与m满足怎样的关系时,
1)AC与⊙O相交?2)AC与⊙O相切?3)AC与⊙O相离?
?
【详解】解:如图,过点O作OD⊥AC于D,
∵∠C=90°,OD⊥AC,∴OD//BC,
∴∠DOA=∠B=30°,∴AD=12OA=12m,∴OD=OA2?AD2=32m,
∴(1)当r>32m时,AC与⊙O相交;
(2)当r=32m时,AC与⊙O相切;
(3)当0?
针对训练
考点六 点/直线与圆的位置关系
4.如图,点A是一个半径为300m的圆形森林公园的中心,在森林公园附近有B,C两村庄,现要在B,C两村庄之间修一条长为1000m的笔直公路将两村连通,现测得∠ABC=45°,∠ACB=30°.问此公路是否会穿过该森林公园?请通过计进行说明?
?
【详解】过点A作AD⊥ BC于点D
∵∠ABC=45°,∠ACB=30°
∴ BD=AD??, AC=2AD
DC=AC2?AD2=(2AD)2?AD2=3AD
∵BC=1000m∴BD+CD=AD+3AD=1000
∴AD=500(3?1)????
而AD=500(3?1) >300
∴公路不会穿过森林公园.
?
知识大全
考点七 切线的判定定理与性质定理
l
A
o
切线的判定定理:
∵OA⊥l于点A,OA是半径
∴直线l是⊙O的切线.
符号语言:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
【提问】要使直线l是⊙O的切线需要满足哪些条件?
①经过半径的外端;②垂直于这条半径.
切线的性质定理:
∵直线l是⊙O的切线,点A的切点
∴OA⊥直线l
符号语言:
圆的切线垂直于过切点的半径.
解题技巧
考点七 切线的判定定理与性质定理
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
解题技巧
考点七 切线的判定定理与性质定理
【利用切线判定定理解题思路一】已知公共点,连半径,证垂直.
【利用切线判定定理解题思路二】未知公共点,作垂线,证半径.
有切线时常用辅助线添加方法: 见切线,连切点,得垂直.
针对训练
考点七 切线的判定定理与性质定理
例8 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
证明:连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB.
∵直线AB经过⊙O上的点C,
∴OC是半径
∴直线AB是⊙O的切线.
针对训练
考点七 切线的判定定理与性质定理
1.已知:OA=OB=5,AB=8,⊙O的直径为6.
求证:直线AB是⊙O的切线.
证明:过点O作OC⊥AB于C,
∵OA=OB=5,AB=8, ∴AC=BC=4.
在Rt△AOC中,根据勾股定理可得:OC=3
∵⊙O的直径为6 ∴OC是⊙O的半径
∴直线AB是⊙O的切线.
针对训练
考点七 切线的判定定理与性质定理
例9 如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
O
P
B
A
解:连接OB,则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r,OP=OA+PA=2+r.
在Rt△OBP中,由勾股定理得
OB2+PB2=PO2,即r2+42=(2+r)2.
解得 r=3,
即⊙O的半径为3.
针对训练
考点七 切线的判定定理与性质定理
1.如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=35°,则∠AOB的度数为( )
A.65° B.55° C.45° D.35°
2. 如图,AB是⊙O的弦,AO的延长线与过点B的⊙O的切线交于点C,如果∠ABO=20°,则∠C的度数是( )
A.70° B.50° C.45° D.20°
知识清单
考点八 切线长定理
经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
切线长的定义:
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
几何语言:
∵PA,PB切?O于点A,B
∴PA=PB,∠APO=∠BPO
针对训练
考点八 切线长定理
例10 如图,PA、PB是⊙O的两条切线,A、B为切点,连结OP
1)图中有哪些相等关系?
2)若连结AB交OP于C,∠PAB和∠PBA相等吗?
3)OP和AB有怎样的位置关系?
4)连结OA、OB,则图中和∠OAC相等的角有哪些?
5)图中和∠ABP相等的角有哪些?
PA=PB,AO=BO
相等
OP垂直平分AB
∠APO,∠BPO,∠OBA
∠BAP,∠AOP,∠BOP
针对训练
考点八 切线长定理
1 如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )
A.130° B.120° C.110° D.100°
2 如图,PA,PB分别与⊙O相切于A、B两点.直线EF切⊙O于C点,分别交PA、PB于E、F,且PA=10.则△PEF的周长为( )
A.10 B.15 C.20 D.25
【详解】解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=4,
∴△PEF的周长=PE+EF+PF=PA+PB=20.
故选:C.
针对训练
考点八 切线长定理
3.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,分别交PA,PB于点C,D.若⊙O的半径为2,∠P=60°,则△PCD的周长等于 _____.
【详解】解:如图,连接OA,OB,OP,
∵PA,PB切⊙O于A,B两点,OA,OB是半径,
∴OA⊥PA,OB⊥PB,且OA=OB,∴PO是∠APB的平分线,
∵∠APB=60°,∴∠APO=30°,∴OP=2OA=4,
在Rt△APO中,由勾股定理得AP=OP2?OA2=23,
∵PA,PB切⊙O于A,B两点,∴PA=PB=23,
∵CD切⊙O于点E,∴AC=CE,BD=DE,
∴△PCD的周长=PC+PD+CD=PC+CA+PD+DB=PA+PB=43,
故答案为:43.
?
知识大全
考点九 三角形的内切圆与外接圆
三角形外接圆的概念:经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形。
三角形内切圆的概念:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
知识大全
考点九 三角形的内切圆与外接圆
{5940675A-B579-460E-94D1-54222C63F5DA}圆心的名称
圆心的确定方法
图形
圆心的性质
外心
内心
三角形三边
中垂线的交点
三角形三条
角平分线的交点
1)OA=OB=OC
2)外心不一定在三角形的内部.
1)到三边的距离相等;
2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
3)内心一定在三角形内部.
解题技巧
考点九 三角形的内切圆与外接圆
1)三角形内切圆半径公式:????=2????????
其中S为三角形的面积;C为三角形的周长.
2)特殊的直角三角形内切圆半径公式:????=????+?????????2或????=????????????+????+????.
其中a,b为直角三角形的直角边长;c为斜边长.
?
针对训练
考点九 三角形的内切圆与外接圆
例11.如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则△ABC内切圆
半径为__________.
1.如图,I为△ABC的内切圆,AB=9,BC=8,AC=10,点D.E分别为AB、AC上的点,且DE为I的切线,则△ADE的周长为_______.
2
【详解】
设DE、BD、BC、CE与I的切点分别为F、 G、H、M,
由切线长定理知:BH=BG、CH=CM、EM=EF、FD=DG、AM=AG;
则AG+AM=AB+AC?BC=11;
所以△ADE的周长=AD+DE+AE=AD+DG+EM+AE
=AG+AM=11.
针对训练
考点九 三角形的内切圆与外接圆
2.已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式—海伦公式S=?????????????????????????????(其中a,b,c是三角形的三边长,p=????+????+????2,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5∴p=????+????+????2=6∴S=???????????????????????????????=6×3×2×1=6
根据上述材料,解答下列问题:
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
?
【详解】解:(1)∵BC=5,AC=6,AB=9,
∴p=????????+????????+????????2=5+6+92=10,
∴S=???????????????????????????????=10×5×4×1=102;
故△ABC的面积102;
?
针对训练
考点九 三角形的内切圆与外接圆
2 已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式—海伦公式S=?????????????????????????????(其中a,b,c是三角形的三边长,p=????+????+????2,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5∴p=????+????+????2=6∴S=???????????????????????????????=6×3×2×1=6
根据上述材料,解答下列问题:
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
?
(2)∵S=12r(AC+BC+AB),
∴102=12r(5+6+9),解得:r=2,
故△ABC的内切圆半径r为2.
?
知识大全
考点十 圆内接正多边形
一个正多边形的外接圆的圆心叫作这个正多边形的中心.
外接圆的半径叫作正多边形的半径.
内切圆的半径叫作正多边形的边心距.
正多边形每一条边所对的圆心角叫做正多边形的中心角.
解题思路
考点十 圆内接正多边形
圆内接正多边形常见辅助线作法:
2)作边心距,构造直角三角形.
1)连半径,得中心角;
3)正多边形半径、边心距和正多边形边长已知其中两个量,第三个量可通过勾股定理求解.
4)若P为正n边形的周长,α为边长,r为边心距,正n边形的周长P为 _______,正n边形的面积为 _______,
an
12anr?或?12Pr
?
5)正n边形的一个内角的度数是____________;中心角是___________;
6)正多边形的中心角与外角的大小关系是________.
?????2×180°????
?
3600????
?
相等
针对训练
考点十 圆内接正多边形
例12.正六边形的边心距为3,则该正六边形的边长是( )
A.3 B.2 C.3 D.23
1.正六边形的边心距为3,则它的周长是(????)
A.6 B.12 C.63 D.123
?
【解析】如图:∵正六边形的边心距为3,∴OB=3,AB=12OA,
∵OA2=AB2+OB2,∴OA2=(12OA)2+(3)2,解得OA=2.故选B.
?
针对训练
考点十 圆内接正多边形
2.正八边形的中心角为______.
3.一个正多边形的一个外角为30°,则它的内角和为_____.
4.若正六边形的边长为3,则其较长的一条对角线长为_____.
5.如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为_____________.
45°
1800°
6
7
知识大全
考点十一 弧长与扇形公式
在半径为R的圆中,n°的圆心角所对的弧长为:????=????180?n????
?
弧长公式:
在半径为R的圆中,圆心角为n°的扇形的面积为:S扇形=nπR2360
?
扇形面积公式:
????扇形=????????????2360=?????????????????2×180=12?????????????180?????=12????????
?
知识大全
考点十一 弧长与扇形公式
r2+h2=l2
S圆锥侧=πrl
S圆锥全= S圆锥侧+ S圆锥底= πrl+πr2
针对训练
考点十一 弧长与扇形公式
例13 若扇形的圆心角为90°,半径为6 cm,则该扇形的弧长为__________ cm.
1.若一弧长为10πcm,此弧所对的圆心角为120°,则该弧所在圆的半径为_________ cm.
2.若一条弧的长为6πcm,弧的半径为6cm,则该弧所对的圆心角为__________ .
3π
15
180°
针对训练
考点十一 弧长与扇形公式
例14.扇形的圆心角为60°,半径为5 ,则这个扇形的弧长_______, 这个扇形的面积为______.
1.已知扇形的圆心角为120°,弧长为20π,扇形面积为 .
2.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角是_________
53????
?
256????
?
300????
?
【详解】解:设这个扇形的半径为r,圆心角是n,面积为S,弧长为l,
由题意得:S=12lr,即240π=12×20πr,
解得:r=24,又由l=nπr180°可得:20π=nπ×24180°,
解得:n=150°,
?
针对训练
考点十一 弧长与扇形公式
3. 如图,折扇完全打开后,OA、OB的夹角为120°,OA的长为30cm,AC的长为20cm,求图中阴影部分的面积S.
解 S=S扇形OAB-S扇形OCD,
针对训练
考点十一 弧长与扇形公式
例15. 已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的侧面积是________cm2.
1. 已知圆锥的母线长为5cm,侧面积为15π cm2 ,则这个圆锥的底面圆半径为_____cm.
2. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是( )
A.5 3 cm B.10cm C.6cm D.5cm
?
3
针对训练
考点十一 弧长与扇形公式
3. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π C.20π D.30π
【解析】
由三视图可知此几何体为圆锥,∴圆锥的底面半径为3,母线长为5,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×3=6π,
∴圆锥的侧面积=12lr=12×6π×5=15π,故选B
?
针对训练
考点十一 弧长与扇形公式
4.若把一个半径为12cm,圆心角为120°的扇形做成圆锥的侧面,则这个圆锥的底面圆的半径是_______,圆锥的高是__________,侧面积是____________.
?
【详解】解:如图,这个圆锥的底面周长为120?????12180=8????,
设半径为r,则有2????????=8????,解得r=4;
圆锥的高是:?=????2?????2=122?42=82,
侧面积为????????????=????×4×12=48????,
故答案为:4;82;48????
?
谢谢!
对称图形——圆
思维导图
知识大全
考点精析
常用技巧或结论
九年级期中考试复习
思维导图
知识大全
考点一 圆的相关概念
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
其中,固定的端点O叫做圆心.
线段OA叫做半径,一般用r表示.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
圆的另一定义(静态):圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形.
知识大全
考点一 圆的相关概念
经过圆心的弦(如图中的AB)叫做直径.
连接圆上任意两点的线段(如图AC)叫做弦.
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB ,读作“圆弧AB”或“弧AB”.
⌒
圆的任意一条直径的两个端点把圆分成的两条弧,每一条弧都叫做半圆.
小于半圆的弧(如图中的AB)叫做劣弧
⌒
大于半圆的弧(用三个字母表示,如图中的ACB)叫做优弧.
⌒
知识大全
考点一 圆的相关概念
圆心相同,半径不相等的两个圆叫做同心圆.
能够互相重合的两个圆叫做等圆.
O
在同圆或等圆中,能够互相重合的弧叫做等弧.
知识大全
考点一 圆的相关概念
圆的轴对称性:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
圆是中心对称图形,圆心就是它的对称中心.
圆的旋转不变性:一个圆绕圆心旋转任意角度,所得图形和原图形重合.
注意事项
考点一 圆的相关概念
一是圆心,圆心确定其位置;
二是半径,半径确定其大小.
【提问】确定一个圆的要素是什么?
1.弦和直径都是线段.
【提问】直径和弦是什么关系呢?
2.凡直径都是弦,是圆中最长的弦,但弦不一定是直径.
【提问】弧、半圆、优弧、劣弧是什么关系呢?
1.弧分为是优弧、劣弧、半圆,
2.半圆是弧,但弧不一定是半圆,
3.半圆既不是劣弧,也不是优弧.
注意事项
考点一 圆的相关概念
[结论]1)等弧的长度一定相等.
2)长度相等的弧不一定是等弧.
3)等弧仅仅存在于同圆或者等圆中.
【提问】长度相等的弧是等弧?
可见这两条弧不可能完全重合,实际上这两条弧弯曲程度不同
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
D
C
A
B
︵
︵
针对训练
考点一 圆的相关概念
例1.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有
A.4个 B.3个 C.2个 D.1个
【详解】解:①经过圆心的弦是直径,即直径是弦,弦不一定是直径,故正确;
②当三点共线的时候,不能作圆,故错误;
③三角形的外心是三角形三边的垂直平分线的交点,所以三角形的外心到三角形各顶点的距离都相等,故正确;
④在同圆或等圆中,能够互相重合的弧是等弧,所以半径相等的两个半圆是等弧,故正确.
故选:B.
针对训练
考点一 圆的相关概念
1.下列条件中,能确定一个圆的是(???????)
A.以点O为圆心 B.以10cm长为半径
C.以点A为圆心,4cm长为半径 D.经过已知点M
2 判断下列说法的正误:
1)弦是直径( )
2)直径是弦( )
3)半径是弦( )
4)直径是圆中最长的弦( )
5)过圆心的线段是直径( )
6)过圆心的直线是直径( )
?
√
√
针对训练
考点一 圆的相关概念
3.如图,请正确的方式表示出以点A为端点的优弧及劣弧.
⌒
⌒
解:优弧:ACD、ACF、ADE、ADC
劣弧:AC、AE、AF、AD
⌒
⌒
⌒
⌒
⌒
⌒
知识大全
考点二 垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理:
符号语言:
∵CD是直径,CD⊥AB
∴ AE=BE, AC?= BC?, A?????= BD.
?
知识大全
考点二 垂径定理
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理推论:
符号语言:
∵CD是直径, AE=BE
∴ CD⊥AB , AC?= BC?, A?????= BD.
?
解题方法
考点二 垂径定理
垂径定理的基本图形:
垂径定理的解题思路:
弦心距:圆心到弦的距离(即圆心到弦的垂线段的距离).
在Rt△OEB中,由勾股定理得:弦心距2+半弦2=半径2
?
垂径定理的解题技巧:
见弦常作弦心距,连接半径,构造直角三角形用勾股定理求解
针对训练
考点二 垂径定理
例2 如图是一个圆弧形门拱,拱高1m ,跨度4m ,那么这个门拱的半径为( )
A.2m B.2.5m C.3m D.5m
【详解】
设这个门拱的半径为r,则OB=r?1,
∵CD=4m,AB⊥CD,
∴BC= CD=2m,
在Rt△BOC中,
∵BC2+OB2=OC2 ,即22 +(r?1) 2 =r2,解得r=2.5m.
故选B.
针对训练
考点二 垂径定理
1. 如图,在?O中,AB=8,OA=5,则OE= ,ED= .
2.如图,在?O中,OA=5,ED=2,则OE= ,AB= .
?
?
?
?
2
3
3
4
3
2
3
8
针对训练
考点二 垂径定理
3.如图,在?O中,AB=8,ED=2,则OA= ,OE= .
?
?
r - 2
r
r2 = (r - 2)2 + 42
5
3
[结论]半径、弦长、弦心距、弓形高中,知二求二.
知识大全
考点三 弧、弦、圆心角的关系
同圆和等圆中,圆心角、弧、弦之间的关系:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.
在同圆或等圆中,相等的弦所对的圆心角相等,所对优弧和劣弧分别相等.
【总结】在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
针对训练
考点三 弧、弦、圆心角的关系
·
C
A
B
D
E
F
O
例3 AB、CD是⊙O的两条弦.
1)如果AB=CD,那么 ___________,_________________.
2)如果AB=CD?,那么 ____________,_____________.
3)如果∠AOB=∠COD,那么 _____________, _____________ .
4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
?
AB=CD
?
∠AOB=∠COD
?
AB=CD
∠AOB=∠COD
?
AB=CD
AB=CD
?
∵AB=CD,∴∠AOB=∠COD.
∵AO=CO,BO=DO,则△AOB ≌ △COD.
而OE、OF是AB与CD对应边上的高,
∴OE=OF.
针对训练
考点三 弧、弦、圆心角的关系
1.如图1,AB是⊙O的直径,BC?=CD?=DE ,∠AOE=66°,则∠COD的度数是( )
A.108° B.72° C.48° D.38°
2. 如图,已知∠????????????=∠????????????,下列结论不一定成立的是( )
A.????????=???????? B.????????=????????
C.△????????????≌△???????????? D.△????????????,△????????????都是等边三角形
?
针对训练
考点三 弧、弦、圆心角的关系
3.如图,AB、CD是⊙O的两条弦,且AB=CD.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,连接OP.下列结论正确的个数是( )
①AB=CD;②OM=ON;③PA=PC;④∠BPO=∠DPO
A.1个 B.2个 C.3个 D.4个
?
【详解】解:如图连接OB、OD;∵AB=CD,∴????????=????????,故①正确
∵OM⊥AB,ON⊥CD,∴AM=MB,CN=ND,∴BM=DN,∵OB=OD∴Rt△OMB≌Rt△OND,
∴OM=ON,故②正确,
∵OP=OP,∴Rt△OPM≌Rt△OPN,∴PM=PN,∠OPB=∠OPD,故④正确,
∵AM=CN,∴PA=PC,故③正确,故选:D.
?
知识大全
考点四 圆周角定理及推论
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
圆周角定理推论:
推论1:同弧或等弧所对的圆周角相等
推论2:直径(或半圆)所对的圆周角是直角;
90°的圆周角所对的弦是直径,所对的弧是半圆.
解题方法
考点四 圆周角定理及推论
圆周角的判断方法:1)顶点在圆上;2)两边都和圆相交.
针对训练
考点四 圆周角定理及推论
例4.如图,⊙O中弦BC与半径OA相交于点D,连接AB,OC,若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25° B.27.5° C.30° D.35°
【解析】
∵∠A=60°,∠ADC=85°,
∴∠B=25°,∠CDO=95°,
∴∠AOC=2∠B=50°,
∴∠C=180°-95°-50°=35°
故选D.
针对训练
考点四 圆周角定理及推论
1.如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是( )
A.40° B.50° C.70° D.80°
2.如图,已知△ACD和△ABE都内接于同一个圆,则∠ADC+∠AEB+∠BAC=( )
A.90° B.180° C.270° D.360°
【详解】∵∠ABC=20°∴∠AOC=40°∵AB是⊙O的弦,OC⊥AB,∴∠AOC=∠BOC=40°,∴∠AOB=80°,故选:D.
【详解】∵∠ADC,∠AEB,∠BAC所对圆弧正好是一个圆周,
∴∠ADC+∠AEB+∠BAC=180°.故选B.
知识大全
考点五 圆内接四边形
圆内接多边形的概念:
如果多边形的所有顶点均在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做多边形的外接圆.
圆内接多边形的性质:
圆内接四边形的对角互补.
针对训练
考点五 圆内接四边形
例5 如图,四边形ABCD内接于⊙O,∠BOD=140°,求∠BCD的度数.
【详解】
∵∠BOD=140°,
∴∠A=12∠BOD=70°,
∴∠BCD=180°﹣∠A=110°.
?
针对训练
考点五 圆内接四边形
1.若四边形????????????????是圆内接四边形,若它的内角∠A:∠C=2:3,则∠????= .
2.如图,已知⊙O的半径为2,ΔABC内接于⊙O,∠ACB=135°,则AB= .
?
72°
?
【详解】连接AD、AE、OA、OB,
∵⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,
∴∠ADB=45°,∴∠AOB=90°,
∵OA=OB=2,∴AB=22,故答案为:22.
?
知识大全
考点六 点/直线与圆的位置关系
r
·
O
A
P
P’
P’’
d<r
d=r
d>r
点P 在⊙O内
点P’在⊙O上
点P”在⊙O外
符号“<=>?”读作“等价于”,
“A<=>B”表示由A条件可推出结论B,B结论可推出条件A.
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
知识大全
考点六 点/直线与圆的位置关系
1)直线与圆没有公共点,称为直线与圆相离.
2)直线与圆只有一个公共点,称为直线与圆相切,这条直线叫做圆的切线,这个公共点叫切点.
3)直线与圆有两个公共点,称为直线与圆相交.
这条直线叫做圆的割线.
切点
切线
割线
解题技巧
考点六 点/直线与圆的位置关系
1)判断点与圆的位置关系的实质是判断点到圆心的距离和半径的大小关系.
2)已知点到圆心的距离与半径的关系,可以确定该点与圆的位置关系,
反过来,由点与圆的位置关系也可以确定该点到圆心的距离与半径的关系.
3)圆的外部可以看成到圆心的距离大于半径的点的集合;.
圆的内部可以看成到圆心的距离小于半径的点的集合.
针对训练
考点六 点/直线与圆的位置关系
例6.已知⊙O的面积为25π:
1)若PO=5.5,则点P在 ;
2)若PO= 4 ,则点P在 ;
3)若PO= ,则点P在圆上;
4)若点P不在圆外,则PO__________.
1.设⊙O的半径为5,圆心的坐标为(0,0),点 P的坐标为(4,-3),
则点P在__________.
圆外
圆内
5
≤5
圆上
针对训练
考点六 点/直线与圆的位置关系
2.圆心为O的两个同心圆,半径分别为1和2,若OP= 3 ,则点P在( )
A.在大圆内 B.在小圆内
C.小圆外 D.大圆内,小圆外
3.在同一平面内,在⊙O外有一个定点P到圆上的距离最长为10,最短为2,则⊙O的半径是( )
A.3 B.4 C.5 D.6
?
o
针对训练
考点六 点/直线与圆的位置关系
例7 已知圆的直径为14cm,设直线和圆心的距离为d :
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
2)若d= 7cm ,则直线与圆______, 直线与圆有____个公共点.
3)若d= 8cm ,则直线与圆______, 直线与圆有____个公共点.
相交
相切
相离
2
1
0
针对训练
考点六 点/直线与圆的位置关系
1.在平面直角坐标系中,以点(﹣2,3)为圆心,半径为3的圆一定(????)
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
2.设⊙O的半径为4cm,直线L上一点A到圆心的距离为4cm,则直线L与⊙O的位置关系是______.
【详解】∵直线上一点到圆心距离为4cm,
∴圆心到直线的距离≤4cm,∴直线与圆相切或相交.
故答案为:相切或相交
针对训练
考点六 点/直线与圆的位置关系
3.在Rt△ABC中,∠C=90°,∠B=30°,O是AB上的一点,OA=m,⊙O的半径为r,当r与m满足怎样的关系时,
1)AC与⊙O相交?2)AC与⊙O相切?3)AC与⊙O相离?
?
【详解】解:如图,过点O作OD⊥AC于D,
∵∠C=90°,OD⊥AC,∴OD//BC,
∴∠DOA=∠B=30°,∴AD=12OA=12m,∴OD=OA2?AD2=32m,
∴(1)当r>32m时,AC与⊙O相交;
(2)当r=32m时,AC与⊙O相切;
(3)当0
针对训练
考点六 点/直线与圆的位置关系
4.如图,点A是一个半径为300m的圆形森林公园的中心,在森林公园附近有B,C两村庄,现要在B,C两村庄之间修一条长为1000m的笔直公路将两村连通,现测得∠ABC=45°,∠ACB=30°.问此公路是否会穿过该森林公园?请通过计进行说明?
?
【详解】过点A作AD⊥ BC于点D
∵∠ABC=45°,∠ACB=30°
∴ BD=AD??, AC=2AD
DC=AC2?AD2=(2AD)2?AD2=3AD
∵BC=1000m∴BD+CD=AD+3AD=1000
∴AD=500(3?1)????
而AD=500(3?1) >300
∴公路不会穿过森林公园.
?
知识大全
考点七 切线的判定定理与性质定理
l
A
o
切线的判定定理:
∵OA⊥l于点A,OA是半径
∴直线l是⊙O的切线.
符号语言:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
【提问】要使直线l是⊙O的切线需要满足哪些条件?
①经过半径的外端;②垂直于这条半径.
切线的性质定理:
∵直线l是⊙O的切线,点A的切点
∴OA⊥直线l
符号语言:
圆的切线垂直于过切点的半径.
解题技巧
考点七 切线的判定定理与性质定理
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
解题技巧
考点七 切线的判定定理与性质定理
【利用切线判定定理解题思路一】已知公共点,连半径,证垂直.
【利用切线判定定理解题思路二】未知公共点,作垂线,证半径.
有切线时常用辅助线添加方法: 见切线,连切点,得垂直.
针对训练
考点七 切线的判定定理与性质定理
例8 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
证明:连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB.
∵直线AB经过⊙O上的点C,
∴OC是半径
∴直线AB是⊙O的切线.
针对训练
考点七 切线的判定定理与性质定理
1.已知:OA=OB=5,AB=8,⊙O的直径为6.
求证:直线AB是⊙O的切线.
证明:过点O作OC⊥AB于C,
∵OA=OB=5,AB=8, ∴AC=BC=4.
在Rt△AOC中,根据勾股定理可得:OC=3
∵⊙O的直径为6 ∴OC是⊙O的半径
∴直线AB是⊙O的切线.
针对训练
考点七 切线的判定定理与性质定理
例9 如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
O
P
B
A
解:连接OB,则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r,OP=OA+PA=2+r.
在Rt△OBP中,由勾股定理得
OB2+PB2=PO2,即r2+42=(2+r)2.
解得 r=3,
即⊙O的半径为3.
针对训练
考点七 切线的判定定理与性质定理
1.如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=35°,则∠AOB的度数为( )
A.65° B.55° C.45° D.35°
2. 如图,AB是⊙O的弦,AO的延长线与过点B的⊙O的切线交于点C,如果∠ABO=20°,则∠C的度数是( )
A.70° B.50° C.45° D.20°
知识清单
考点八 切线长定理
经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
切线长的定义:
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
几何语言:
∵PA,PB切?O于点A,B
∴PA=PB,∠APO=∠BPO
针对训练
考点八 切线长定理
例10 如图,PA、PB是⊙O的两条切线,A、B为切点,连结OP
1)图中有哪些相等关系?
2)若连结AB交OP于C,∠PAB和∠PBA相等吗?
3)OP和AB有怎样的位置关系?
4)连结OA、OB,则图中和∠OAC相等的角有哪些?
5)图中和∠ABP相等的角有哪些?
PA=PB,AO=BO
相等
OP垂直平分AB
∠APO,∠BPO,∠OBA
∠BAP,∠AOP,∠BOP
针对训练
考点八 切线长定理
1 如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )
A.130° B.120° C.110° D.100°
2 如图,PA,PB分别与⊙O相切于A、B两点.直线EF切⊙O于C点,分别交PA、PB于E、F,且PA=10.则△PEF的周长为( )
A.10 B.15 C.20 D.25
【详解】解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=4,
∴△PEF的周长=PE+EF+PF=PA+PB=20.
故选:C.
针对训练
考点八 切线长定理
3.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,分别交PA,PB于点C,D.若⊙O的半径为2,∠P=60°,则△PCD的周长等于 _____.
【详解】解:如图,连接OA,OB,OP,
∵PA,PB切⊙O于A,B两点,OA,OB是半径,
∴OA⊥PA,OB⊥PB,且OA=OB,∴PO是∠APB的平分线,
∵∠APB=60°,∴∠APO=30°,∴OP=2OA=4,
在Rt△APO中,由勾股定理得AP=OP2?OA2=23,
∵PA,PB切⊙O于A,B两点,∴PA=PB=23,
∵CD切⊙O于点E,∴AC=CE,BD=DE,
∴△PCD的周长=PC+PD+CD=PC+CA+PD+DB=PA+PB=43,
故答案为:43.
?
知识大全
考点九 三角形的内切圆与外接圆
三角形外接圆的概念:经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形。
三角形内切圆的概念:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
知识大全
考点九 三角形的内切圆与外接圆
{5940675A-B579-460E-94D1-54222C63F5DA}圆心的名称
圆心的确定方法
图形
圆心的性质
外心
内心
三角形三边
中垂线的交点
三角形三条
角平分线的交点
1)OA=OB=OC
2)外心不一定在三角形的内部.
1)到三边的距离相等;
2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
3)内心一定在三角形内部.
解题技巧
考点九 三角形的内切圆与外接圆
1)三角形内切圆半径公式:????=2????????
其中S为三角形的面积;C为三角形的周长.
2)特殊的直角三角形内切圆半径公式:????=????+?????????2或????=????????????+????+????.
其中a,b为直角三角形的直角边长;c为斜边长.
?
针对训练
考点九 三角形的内切圆与外接圆
例11.如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则△ABC内切圆
半径为__________.
1.如图,I为△ABC的内切圆,AB=9,BC=8,AC=10,点D.E分别为AB、AC上的点,且DE为I的切线,则△ADE的周长为_______.
2
【详解】
设DE、BD、BC、CE与I的切点分别为F、 G、H、M,
由切线长定理知:BH=BG、CH=CM、EM=EF、FD=DG、AM=AG;
则AG+AM=AB+AC?BC=11;
所以△ADE的周长=AD+DE+AE=AD+DG+EM+AE
=AG+AM=11.
针对训练
考点九 三角形的内切圆与外接圆
2.已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式—海伦公式S=?????????????????????????????(其中a,b,c是三角形的三边长,p=????+????+????2,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5∴p=????+????+????2=6∴S=???????????????????????????????=6×3×2×1=6
根据上述材料,解答下列问题:
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
?
【详解】解:(1)∵BC=5,AC=6,AB=9,
∴p=????????+????????+????????2=5+6+92=10,
∴S=???????????????????????????????=10×5×4×1=102;
故△ABC的面积102;
?
针对训练
考点九 三角形的内切圆与外接圆
2 已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式—海伦公式S=?????????????????????????????(其中a,b,c是三角形的三边长,p=????+????+????2,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5∴p=????+????+????2=6∴S=???????????????????????????????=6×3×2×1=6
根据上述材料,解答下列问题:
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
?
(2)∵S=12r(AC+BC+AB),
∴102=12r(5+6+9),解得:r=2,
故△ABC的内切圆半径r为2.
?
知识大全
考点十 圆内接正多边形
一个正多边形的外接圆的圆心叫作这个正多边形的中心.
外接圆的半径叫作正多边形的半径.
内切圆的半径叫作正多边形的边心距.
正多边形每一条边所对的圆心角叫做正多边形的中心角.
解题思路
考点十 圆内接正多边形
圆内接正多边形常见辅助线作法:
2)作边心距,构造直角三角形.
1)连半径,得中心角;
3)正多边形半径、边心距和正多边形边长已知其中两个量,第三个量可通过勾股定理求解.
4)若P为正n边形的周长,α为边长,r为边心距,正n边形的周长P为 _______,正n边形的面积为 _______,
an
12anr?或?12Pr
?
5)正n边形的一个内角的度数是____________;中心角是___________;
6)正多边形的中心角与外角的大小关系是________.
?????2×180°????
?
3600????
?
相等
针对训练
考点十 圆内接正多边形
例12.正六边形的边心距为3,则该正六边形的边长是( )
A.3 B.2 C.3 D.23
1.正六边形的边心距为3,则它的周长是(????)
A.6 B.12 C.63 D.123
?
【解析】如图:∵正六边形的边心距为3,∴OB=3,AB=12OA,
∵OA2=AB2+OB2,∴OA2=(12OA)2+(3)2,解得OA=2.故选B.
?
针对训练
考点十 圆内接正多边形
2.正八边形的中心角为______.
3.一个正多边形的一个外角为30°,则它的内角和为_____.
4.若正六边形的边长为3,则其较长的一条对角线长为_____.
5.如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为_____________.
45°
1800°
6
7
知识大全
考点十一 弧长与扇形公式
在半径为R的圆中,n°的圆心角所对的弧长为:????=????180?n????
?
弧长公式:
在半径为R的圆中,圆心角为n°的扇形的面积为:S扇形=nπR2360
?
扇形面积公式:
????扇形=????????????2360=?????????????????2×180=12?????????????180?????=12????????
?
知识大全
考点十一 弧长与扇形公式
r2+h2=l2
S圆锥侧=πrl
S圆锥全= S圆锥侧+ S圆锥底= πrl+πr2
针对训练
考点十一 弧长与扇形公式
例13 若扇形的圆心角为90°,半径为6 cm,则该扇形的弧长为__________ cm.
1.若一弧长为10πcm,此弧所对的圆心角为120°,则该弧所在圆的半径为_________ cm.
2.若一条弧的长为6πcm,弧的半径为6cm,则该弧所对的圆心角为__________ .
3π
15
180°
针对训练
考点十一 弧长与扇形公式
例14.扇形的圆心角为60°,半径为5 ,则这个扇形的弧长_______, 这个扇形的面积为______.
1.已知扇形的圆心角为120°,弧长为20π,扇形面积为 .
2.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角是_________
53????
?
256????
?
300????
?
【详解】解:设这个扇形的半径为r,圆心角是n,面积为S,弧长为l,
由题意得:S=12lr,即240π=12×20πr,
解得:r=24,又由l=nπr180°可得:20π=nπ×24180°,
解得:n=150°,
?
针对训练
考点十一 弧长与扇形公式
3. 如图,折扇完全打开后,OA、OB的夹角为120°,OA的长为30cm,AC的长为20cm,求图中阴影部分的面积S.
解 S=S扇形OAB-S扇形OCD,
针对训练
考点十一 弧长与扇形公式
例15. 已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的侧面积是________cm2.
1. 已知圆锥的母线长为5cm,侧面积为15π cm2 ,则这个圆锥的底面圆半径为_____cm.
2. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是( )
A.5 3 cm B.10cm C.6cm D.5cm
?
3
针对训练
考点十一 弧长与扇形公式
3. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π C.20π D.30π
【解析】
由三视图可知此几何体为圆锥,∴圆锥的底面半径为3,母线长为5,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×3=6π,
∴圆锥的侧面积=12lr=12×6π×5=15π,故选B
?
针对训练
考点十一 弧长与扇形公式
4.若把一个半径为12cm,圆心角为120°的扇形做成圆锥的侧面,则这个圆锥的底面圆的半径是_______,圆锥的高是__________,侧面积是____________.
?
【详解】解:如图,这个圆锥的底面周长为120?????12180=8????,
设半径为r,则有2????????=8????,解得r=4;
圆锥的高是:?=????2?????2=122?42=82,
侧面积为????????????=????×4×12=48????,
故答案为:4;82;48????
?
谢谢!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
