第一章 一元二次方程【考点串讲PPT(共38张)】-2023-2024学年九年级数学上学期期中考点大串讲(苏科版)
文档属性
| 名称 | 第一章 一元二次方程【考点串讲PPT(共38张)】-2023-2024学年九年级数学上学期期中考点大串讲(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 21:39:47 | ||
图片预览











文档简介
第一章
一元二次方程
思维导图
知识大全
考点精析
常用技巧或结论
九年级期中考试复习
思维导图
知识大全
考点一 一元二次方程
只含有_______未知数(元),并且未知数最高次数是_____,等号两边都是________,这样的方程叫一元二次方程。
一个
2
整式
ax 2 + bx + c = 0(a≠0)
一元二次方程的一般形式为___________________________________。
二次项
一次项
常数项
二次项系数
一次项系数
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫一元二次方程的根。
解题技巧
考点一 一元二次方程
判断一元二次方程五大条件(缺一不可):
1.只有一个未知数;
2.未知数的最高次数是2次;
3.二次项系数不为0;
4.整式方程;
5.先化简后判断.
针对训练
考点一 一元二次方程
【典例1】要使方程a?3x2+b+1x+c=0是关于x的一元二次方程,则( )
A.a≠0 B.a≠3 C.a≠3且b≠-1 D.a≠3且b≠-1且c≠0
1.下列方程中,一元二次方程共有( )
①x2?3x?1=0;②x?22+y2=3;③1x2+2x?8=0;④?2x2=0;
A.1个 B.2个 C.3个 D.4个
?
针对训练
考点一 一元二次方程
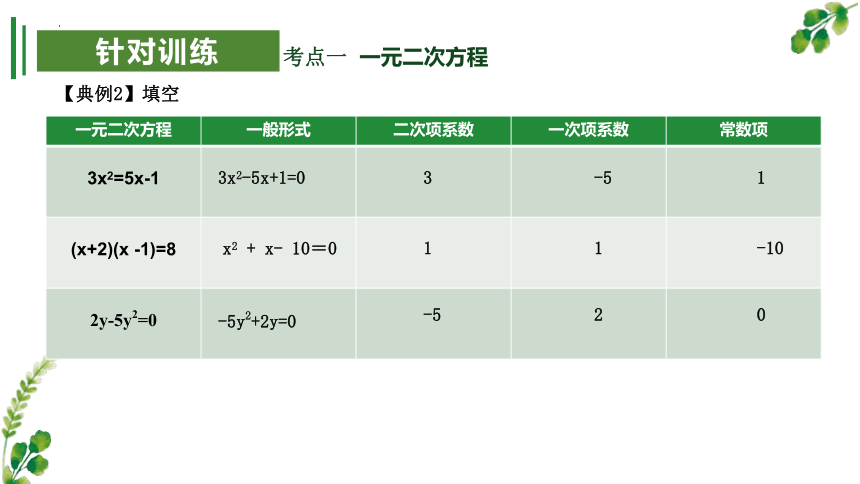
【典例2】填空
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}一元二次方程
一般形式
二次项系数
一次项系数
常数项
3x2=5x-1
(x+2)(x -1)=8
2y-5y2=0
3x2-5x+1=0
x2 + x- 10=0
-5y2+2y=0
3
-5
1
1
1
-10
-5
2
0
针对训练
考点一 一元二次方程
【典例3】若x=-1是方程ax2+bx+c=0的解,则( )
A.a+b+c=1 B.a﹣b+c=0
C.a+b+c=0 D.a﹣b﹣c=0
1.若一元二次方程的二次项系数为1,常数项为0,它的一个根为2,则该方程为
_______________.
2.已知x=n是关于x的一元二次方程mx2﹣4x﹣5=0的一个根,若mn2﹣4n+m=6,
求m的值.
x2-2x=0
【详解】依题意,得????????2?4?????5=0.
∴????????2?4????=5.
∵????????2?4????+????=6,
∴5+????=6.∴????=1.
?
知识大全
考点一 一元二次方程
3.(2022广东14/23)若????=1是方程????2?2????+????=0的根,则????=____________.
?
【详解】把x=1代入方程x2?2x+a=0,得1?2+a=0,解得a=1,故答案为:1.
?
4.(2022资阳市14/24)若a是一元二次方程x2+2x?3=0的一个根,则2a2+4a的值是___________.
?
【详解】∵a是一元二次方程x2+2x?3=0的一个根,
∴a2+2a?3=0,
∴a2+2a=3,
∴2a2+4a=2a2+2a=2×3=6,
故答案为:6.
?
知识大全
考点二 一元二次方程与一元一次方程
一元一次方程与一元二次方程相同点与不同点?
一元一次方程
一元二次方程
一般形式
相同点
不同点
ax=b (a≠0)
ax2+bx+c=0 (a≠0)
整式方程,只含有一个未知数
未知数最高次数是1
未知数最高次数是2
解题技巧
考点二 一元二次方程与一元一次方程
一元二次方程的定义:只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件,这是在做题过程中容易忽视的知识点.
一元一次方程的定义:只有一个未知数且未知数最高次数为1的整式方程叫做一元一次方程,一般形式是ax+b=0(且a≠0).
针对训练
考点二 一元二次方程与一元一次方程
【典例4】已知关于x的方程(2k+1)x2+4kx+k-1=0,问:
(1)k为何值时,此方程是一元一次方程?
(2)k为何值时,此方程是一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数及常数项.
【解答】
解:(1)∵2????+1????2+4????????+?????1=0是关于x的一元一次方程,
∴2????+1=04????≠0,解得????=?12
(2)∵2????+1????2+4????????+?????1=0是关于x的一元二次方程,
∴2????+1≠0即????≠?12,
∴这个一元二次方程的二次项系数为2k+1,一次项系数为4????,常数项为k-1
?
针对训练
考点二 一元二次方程与一元一次方程
1.简答题:
(1)当????为何值时,关于????的方程????2?1????2+?????????2=0是一元二次方程?
(2)已知关于????的一元二次方程????2?1????2+?????????3?????=0有一个根是0,求????的值.
(3)在第(2)题中,如果要使已知方程有一个根是l,那么m应该等于什么数?
?
【详解】
解:(1)∵关于????的方程????2?1????2+?????????2=0是一元二次方程,
∴????2?1≠0,解得:????≠±1;
(2)∵关于????的一元二次方程????2?1????2+?????????3?????=0有一个根是0,
∴将x=0代入????2?1????2+?????????3?????=0可得:?3?????=0,解得:m=-3;
(3)∵关于????的一元二次方程????2?1????2+?????????3?????=0有一个根是1,
∴将x=1代入????2?1????2+?????????3?????=0可得:????2?4=0,解得:m=±2.
?
知识大全
考点三 解一元二次方程
一般地,对于方程x2=p ①,
1)当p>0时,根据平方根的意义,方程①有两个____________的实数根______________________;
2)当p=0时,方程①有两个______的实数根_____________;
3)当p<0时,因为对于任意实数x,都有x2____0,所以方程① _______实数根。
不相等
相等
x1=x2=0
无
≥
x1=-???? , x2= ????
?
知识大全
考点三 解一元二次方程
将方程通过配成____________形式来解一元二次方程的方法,叫做配方法。配方是为了___________,把一个一元二次方程转化成______一元一次方程来解。
用配方法解一元二次方程的关键:
将一元二次方程配成完全平方形式。
完全平方
降次
两个
不能直接开平方
解的一元二次方程
可以直接开平方
解的一元二次方程
变形为
知识大全
考点三 解一元二次方程
一般地,如果一个一元二次方程通过配方转化成(x+n)2=p ①
的形式,那么就有:
1)当p>0时,根据平方根的意义,方程①有两个________________的实数根______________________;
2)当p=0时,方程①有两个________________的实数根______________________;
3)当p<0时,因为对于任意实数x,都有(x+n)2____0,所以方程①_______实数根。
不相等
相等
x1=x2=-n
无
≥
x1=-n-????,x2=-n+ ????
?
知识大全
考点三 解一元二次方程
当Δ≥0时,方程ax2+bx+c=0(a≠0)的实数根为_____________的形式,这个式子叫做一元二次方程 ax2+bx+c=0的求根公式。
解一元二次方程时,把各系数直接________________,可以省略配方过程而直接求一元二次方程根,这种解一元二次方程的方法叫做公式法。
?
????=?????±?????????????????????????????
?
代入求根公式
知识大全
考点三 解一元二次方程
先因式分解,使一元二次方程转化为____________________的形式,从而实现________,这种解一元二次方程的方法叫做因式分解法。
两个一次式乘积等于0
降次
知识大全
考点三 解一元二次方程
解一元二次方程的方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
解一元二次方程的方法
适用范围
配方法
(基础)
先配方,再降次
所有一元二次方程
公式法
(基础)
利用求根公式
所有一元二次方程
因式分解法
(灵活掌握)
右化零,左分解,两因式,各求解
仅部分
解一元二次方程的基本思路是:将二次方程化为一次方程,即降次。
针对训练
考点三 解一元二次方程
【典例4】用适当的方法解下列方程:
1)?????22=4?????2????2
2)?????1????+2=4
?
【详解】
(1)解:(1)(x﹣2)2=4x﹣2x2,
整理,得(x﹣2+2x)(x﹣2)=0,
解得:x1=23,x2=2;
(2)解:(x﹣1)(x+2)=4,
整理,得x2+x﹣6=0,
解得:x1=﹣3,x2=2.
?
针对训练
考点三 解一元二次方程
(1)解:?????12=4,
解得:????1=3,????2=?1;
(2)????2?6?????18=0
∴????2?6????=18,
∴????2?6????+9=27,
即?????32=27,
∴?????3=±33,
解得:????1=3+33,????2=3?33;
(3)3?????22=?????????2
∴3?????22??????????2=0,
∴?????22?????6=0,
解得:????1=2,????2=3;
?
1解方程:
(1)?????12=4
(2)????2?6?????18=0
(3)3?????22=?????????2
?
针对训练
考点三 解一元二次方程
2.下列方程中,适合用直接开方法解的个数有( )
① 13x2=1;②(x﹣2)2=5;③14(x+3)2=3;④x2=x+3;⑤3x2﹣3=x2+1;
⑥y2﹣2y﹣3=0
A.1 B.2 C.3 D.4
3.用配方法解方程x2﹣23x﹣1=0时,应将其变形为( )
A.(x﹣13)2=89 B.(x+13)2=109????C.(x﹣23)2=0 D.(x﹣13)2=109
?
针对训练
考点三 解一元二次方程
4.下列一元二次方程最适合用分解因式法解的是( )
A.(x-1)(x-2)=3 B.x2 +4x=23
C.x2+2x-1=0 D.(x-3)2=x2-9
5.已知x、y都是实数,且(x2+y2)(x2+y2+2)﹣3=0,那么x2+y2的值是( )
A.﹣3 B.1 C.﹣3或1 D.﹣1或3
知识大全
考点四 一元二次方程根的判别式
一般地,式子b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式。
判别式概念:
判别式表示:
通常用希腊字母“Δ”表示,即Δ=b2-4ac.
(x+b2a)2=b2?4ac4a2=Δ4a2
?
由前面的推导过程,可知:
1)若△>0,一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实根。
2)若△= 0,一元二次方程ax2+bx+c=0(a≠0)有两个 相等的实根。
3)若△<0,一元二次方程ax2+bx+c=0(a≠0) 无 实根。
即当Δ≥0时,方程ax2+bx+c=0(a≠0)的实数根为
解题技巧
考点四 一元二次方程根的判别式
一元二次方程????????2+????????+????=0(????≠0) 根的判别式:????=????2?4????????
1)????>0?方程有两个不相等的实根:????=?????±????2?4????????2????(????2?4????????≥0)
2)????=0?方程有两个相等的实根:????1=????2=?????2????
3)??<0?方程无实根
【选择题快速判断法】如果a、c异号,所以ac<0,则????>0,方程有两个不相等的实根.
?
针对训练
考点四 一元二次方程根的判别式
【典例5】关于????的一元二次方程????2?????+3????+2????+1=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.有两个实数根 D.没有实数根
1.已知关于x的一元二次方程????2+2x?????=0有两个相等的实数根,则a的值是( )
A.4 B.﹣4 C.1 D.﹣1
2.方程(?????2)????2?4?????1=0有两个不等的实数根,则????的取值范围是( ).
A.????>??2 B.?????2且????≠2
?
针对训练
考点四 一元二次方程根的判别式
3. (青海省西宁市城区2022年中考数学真题)关于x的一元二次方程2x2+x?k=0没有实数根,则k的取值范围是(???????)
A.k?18 D.k≥?18
4.(2022年甘肃省兰州市中考数学真题)关于x的一元二次方程kx2+2x?1=0有两个相等的实数根,则k=(???????)
A.-2 B.-1 C.0 D.1
?
【详解】解:∵一元二次方程2????2+?????????=0没有实数根,
∴Δ=12?4×2×(?k)<0,解得?????
【详解】
∵原方程有两个相等的实数根,
∴△=b2?4ac=4?4×(?k)=0,且k≠0;
解得????=?1.
故选:B.
?
知识大全
考点五 一元二次方程根与系数的关系
当Δ?≥0时,两根的和等于一次项系数与二次项系数的___________,
两根的积等于常数项与二次项系数的___________,
即方程ax2+bx+c=0(a≠0),根与系数的关系为:
人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”。
?
【易错点】使用韦达定理的前提条件:1) 先把方程化为一般式。
2) Δ≥0。
比的相反数
比
x1+x2 =?ba, x1x2 = ca
?
解题技巧
考点五 一元二次方程根与系数的关系
已知一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2
1)平方和 ????????????+????????????=
2)倒数和 ???????????? + ????????????? =
3)差的绝对值 | x1 - x2 |=
4)????1????2+????2????1 =
5)(????1+1)(????2+1)=
?
(????????+????????)?????????????????????????
?
????????+????????????????????????
?
(?????????????????)????=(????????+????????)?????????????????????????
?
????12+????22????1????2=(????1+????2)2?2????1????2????1????2
?
????1????2+(????1+????2)+1
?
针对训练
考点五 一元二次方程根与系数的关系
【典例6】已知关于x的一元二次方程????2+3????+?????2=0有实数根.
(1)求实数k的取值范围.
(2)设方程的两个实数根分别为????1,????2,若????1+1????2+1=?1,求k的值.
?
【详解】(1)解:∵一元二次方程????2+3????+?????2=0有实数根.
∴?≥0,即32-4(k-2)≥0, 解得k≤174
(2)∵方程的两个实数根分别为????1,????2,
∴????1+????2=?3,????1????2=?????2,
∵????1+1????2+1=?1,
∴????1????2+????1+????2+1=?1,
∴?????2?3+1=?1,
解得k=3.
?
针对训练
考点五 一元二次方程根与系数的关系
1.已知关于x的一元二次方程????2?4?????2????+8=0有两个实数根????1,????2.
(1)求k的取值范围;
(2)若????13????2+????1????23=24,求k的值.
?
【详解】解:(1)由题意可知,????=(?4)2?4×1×(?2????+8)≥0,
整理得:16+8?????32≥0,
解得:????≥2,
∴????的取值范围是:????≥2.
故答案为:????≥2.
?
针对训练
考点五 一元二次方程根与系数的关系
2.已知关于x的一元二次方程????2?4?????2????+8=0有两个实数根????1,????2.
(1)求k的取值范围;
(2)若????13????2+????1????23=24,求k的值.
?
(2)由题意得:????13????2+????1????23=????1????2(????1+????2)2?2????1????2=24,
由韦达定理可知:????1+????2=4,????1????2=?2????+8,
故有:(?2????+8)42?2(?2????+8)=24,
整理得:????2?4????+3=0,
解得:????1=3,????2=1,
又由(1)中可知????≥2,
∴????的值为????=3.
故答案为:????=3.
?
针对训练
考点五 一元二次方程根与系数的关系
3.(2022年湖北省十堰市中考数学真题)已知关于????的一元二次方程????2?2?????3????2=0.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根分别为????,????,且????+2????=5,求????的值.
?
【解析】
(1)Δ=????2?4????????=?22?4×1?(?3????2)=4+12????2,
∵12????2≥0,∴4+12????2≥4>0,∴该方程总有两个不相等的实数根;
(2)∵方程的两个实数根????,????,由根与系数关系可知,????+????=2,?????????=?3????2,
∵????+2????=5,∴????=5?2????,
∴5?2????+????=2,解得:????=3,????=?1,
∴?3????2=?1×3=?3,
即????=±1.
?
解题技巧
考点六 利用一元二次方程解决实际问题
利用一元二次方程解决实际问题:
1)传播问题:明确每轮传播中的___________个数,以及这一轮被传染的__________.
2) 增长率问题:
①如果增长率问题中的基数为a,平均增长率为x,则第一次增长后的数量为
____________,第二次增长后的数量为____________.
②如果下降率问题中的基数为a,平均下降率为x,则第一次下降后的数量为
__________,第二次下降后的数量为___________.
3)几何问题:
①常见几何____________是等量关系。
②解决课本封面、小路宽度常采用____________列方程。
传染源
总数
a(1+x)
a(1+x)2
a(1-x)
a(1-x)2
周长面积
图形平移
解题技巧
考点六 利用一元二次方程解决实际问题
利用一元二次方程解决实际问题:
4) 数字问题:
①若个位数字为a,十位数字为b,百位数字为c,则十位数字表示为____________.
百位数字表示_____________.
②日历中的某个日期,左右相差___________,上下相差___________.
5)利润问题:单件利润=___________,总利润=________________
6) 表格问题:理解题干内容,从题干中获取信息。
7)动点问题:在动点中观察图形的变化情况,需理解动点在图形不同位置情况,才
能做好计算推理过程。在变化中找到不变的性质是解决动点问题的基本思路。
100c+10b+a
10b+a
1
7
售价-进价
单件利润×销量
针对训练
考点六 利用一元二次方程解决实际问题
1.“新冠肺炎”防治取得战略性成果.若有一个人患了“新冠肺炎”,经过两轮传染后共有25个人患了“新冠肺炎”,则每轮传染中平均一个人传染了_________人.
【详解】设每轮传染中平均一个人传染了x人,则第一轮传染中有x人被传染,第二轮传染中有????(1+????)人被传染,由题意得 1+????+????(1+????)=25
解得????=4或?6(舍去)所以,每轮传染中平均一个人传染了4人,故答案为:4.
?
【详解】设十位上的数字为x,则个位上的数字为(x﹣4).
可列方程为:x2+(x﹣4)2=10x+(x﹣4)﹣4
解得:x1=8,x2=1.5(舍),∴x﹣4=4,
∴10x+(x﹣4)=84.
答:这个两位数为84.故答案为:84
2.已知一个两位数,个位上的数字比十位上的数字小4,且个位上的数字与十位上的数字的平方和比这个两位数小4,则这个两位数是___.
针对训练
考点六 利用一元二次方程解决实际问题
【详解】解:由题意得:
50?????300+10????=16000;
故答案为50?????300+10????=16000.
?
3.2021年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价????元,可列方程________.
?
针对训练
考点六 利用一元二次方程解决实际问题
4.已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于210cm?
(3)△PQB的面积能否等于7 平方厘米?请说明理由.
?
【提示】(1)设P、Q分别从A、B两点出发,x秒后,AP=xcm,PB=(5-x)cm,BQ=2xcm,则△PBQ的面积等于12×2x(5-x),令该式等于4,列出方程求出符合题意的解;
(2)利用勾股定理列出方程求解即可;
(3)看△PBQ的面积能否等于7cm2,只需令12×2t(5-t)=7,化简该方程后,判断该方程的????2?4????????与0的关系,大于或等于0则可以,否则不可以.
?
谢谢!
一元二次方程
思维导图
知识大全
考点精析
常用技巧或结论
九年级期中考试复习
思维导图
知识大全
考点一 一元二次方程
只含有_______未知数(元),并且未知数最高次数是_____,等号两边都是________,这样的方程叫一元二次方程。
一个
2
整式
ax 2 + bx + c = 0(a≠0)
一元二次方程的一般形式为___________________________________。
二次项
一次项
常数项
二次项系数
一次项系数
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫一元二次方程的根。
解题技巧
考点一 一元二次方程
判断一元二次方程五大条件(缺一不可):
1.只有一个未知数;
2.未知数的最高次数是2次;
3.二次项系数不为0;
4.整式方程;
5.先化简后判断.
针对训练
考点一 一元二次方程
【典例1】要使方程a?3x2+b+1x+c=0是关于x的一元二次方程,则( )
A.a≠0 B.a≠3 C.a≠3且b≠-1 D.a≠3且b≠-1且c≠0
1.下列方程中,一元二次方程共有( )
①x2?3x?1=0;②x?22+y2=3;③1x2+2x?8=0;④?2x2=0;
A.1个 B.2个 C.3个 D.4个
?
针对训练
考点一 一元二次方程
【典例2】填空
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}一元二次方程
一般形式
二次项系数
一次项系数
常数项
3x2=5x-1
(x+2)(x -1)=8
2y-5y2=0
3x2-5x+1=0
x2 + x- 10=0
-5y2+2y=0
3
-5
1
1
1
-10
-5
2
0
针对训练
考点一 一元二次方程
【典例3】若x=-1是方程ax2+bx+c=0的解,则( )
A.a+b+c=1 B.a﹣b+c=0
C.a+b+c=0 D.a﹣b﹣c=0
1.若一元二次方程的二次项系数为1,常数项为0,它的一个根为2,则该方程为
_______________.
2.已知x=n是关于x的一元二次方程mx2﹣4x﹣5=0的一个根,若mn2﹣4n+m=6,
求m的值.
x2-2x=0
【详解】依题意,得????????2?4?????5=0.
∴????????2?4????=5.
∵????????2?4????+????=6,
∴5+????=6.∴????=1.
?
知识大全
考点一 一元二次方程
3.(2022广东14/23)若????=1是方程????2?2????+????=0的根,则????=____________.
?
【详解】把x=1代入方程x2?2x+a=0,得1?2+a=0,解得a=1,故答案为:1.
?
4.(2022资阳市14/24)若a是一元二次方程x2+2x?3=0的一个根,则2a2+4a的值是___________.
?
【详解】∵a是一元二次方程x2+2x?3=0的一个根,
∴a2+2a?3=0,
∴a2+2a=3,
∴2a2+4a=2a2+2a=2×3=6,
故答案为:6.
?
知识大全
考点二 一元二次方程与一元一次方程
一元一次方程与一元二次方程相同点与不同点?
一元一次方程
一元二次方程
一般形式
相同点
不同点
ax=b (a≠0)
ax2+bx+c=0 (a≠0)
整式方程,只含有一个未知数
未知数最高次数是1
未知数最高次数是2
解题技巧
考点二 一元二次方程与一元一次方程
一元二次方程的定义:只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件,这是在做题过程中容易忽视的知识点.
一元一次方程的定义:只有一个未知数且未知数最高次数为1的整式方程叫做一元一次方程,一般形式是ax+b=0(且a≠0).
针对训练
考点二 一元二次方程与一元一次方程
【典例4】已知关于x的方程(2k+1)x2+4kx+k-1=0,问:
(1)k为何值时,此方程是一元一次方程?
(2)k为何值时,此方程是一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数及常数项.
【解答】
解:(1)∵2????+1????2+4????????+?????1=0是关于x的一元一次方程,
∴2????+1=04????≠0,解得????=?12
(2)∵2????+1????2+4????????+?????1=0是关于x的一元二次方程,
∴2????+1≠0即????≠?12,
∴这个一元二次方程的二次项系数为2k+1,一次项系数为4????,常数项为k-1
?
针对训练
考点二 一元二次方程与一元一次方程
1.简答题:
(1)当????为何值时,关于????的方程????2?1????2+?????????2=0是一元二次方程?
(2)已知关于????的一元二次方程????2?1????2+?????????3?????=0有一个根是0,求????的值.
(3)在第(2)题中,如果要使已知方程有一个根是l,那么m应该等于什么数?
?
【详解】
解:(1)∵关于????的方程????2?1????2+?????????2=0是一元二次方程,
∴????2?1≠0,解得:????≠±1;
(2)∵关于????的一元二次方程????2?1????2+?????????3?????=0有一个根是0,
∴将x=0代入????2?1????2+?????????3?????=0可得:?3?????=0,解得:m=-3;
(3)∵关于????的一元二次方程????2?1????2+?????????3?????=0有一个根是1,
∴将x=1代入????2?1????2+?????????3?????=0可得:????2?4=0,解得:m=±2.
?
知识大全
考点三 解一元二次方程
一般地,对于方程x2=p ①,
1)当p>0时,根据平方根的意义,方程①有两个____________的实数根______________________;
2)当p=0时,方程①有两个______的实数根_____________;
3)当p<0时,因为对于任意实数x,都有x2____0,所以方程① _______实数根。
不相等
相等
x1=x2=0
无
≥
x1=-???? , x2= ????
?
知识大全
考点三 解一元二次方程
将方程通过配成____________形式来解一元二次方程的方法,叫做配方法。配方是为了___________,把一个一元二次方程转化成______一元一次方程来解。
用配方法解一元二次方程的关键:
将一元二次方程配成完全平方形式。
完全平方
降次
两个
不能直接开平方
解的一元二次方程
可以直接开平方
解的一元二次方程
变形为
知识大全
考点三 解一元二次方程
一般地,如果一个一元二次方程通过配方转化成(x+n)2=p ①
的形式,那么就有:
1)当p>0时,根据平方根的意义,方程①有两个________________的实数根______________________;
2)当p=0时,方程①有两个________________的实数根______________________;
3)当p<0时,因为对于任意实数x,都有(x+n)2____0,所以方程①_______实数根。
不相等
相等
x1=x2=-n
无
≥
x1=-n-????,x2=-n+ ????
?
知识大全
考点三 解一元二次方程
当Δ≥0时,方程ax2+bx+c=0(a≠0)的实数根为_____________的形式,这个式子叫做一元二次方程 ax2+bx+c=0的求根公式。
解一元二次方程时,把各系数直接________________,可以省略配方过程而直接求一元二次方程根,这种解一元二次方程的方法叫做公式法。
?
????=?????±?????????????????????????????
?
代入求根公式
知识大全
考点三 解一元二次方程
先因式分解,使一元二次方程转化为____________________的形式,从而实现________,这种解一元二次方程的方法叫做因式分解法。
两个一次式乘积等于0
降次
知识大全
考点三 解一元二次方程
解一元二次方程的方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
解一元二次方程的方法
适用范围
配方法
(基础)
先配方,再降次
所有一元二次方程
公式法
(基础)
利用求根公式
所有一元二次方程
因式分解法
(灵活掌握)
右化零,左分解,两因式,各求解
仅部分
解一元二次方程的基本思路是:将二次方程化为一次方程,即降次。
针对训练
考点三 解一元二次方程
【典例4】用适当的方法解下列方程:
1)?????22=4?????2????2
2)?????1????+2=4
?
【详解】
(1)解:(1)(x﹣2)2=4x﹣2x2,
整理,得(x﹣2+2x)(x﹣2)=0,
解得:x1=23,x2=2;
(2)解:(x﹣1)(x+2)=4,
整理,得x2+x﹣6=0,
解得:x1=﹣3,x2=2.
?
针对训练
考点三 解一元二次方程
(1)解:?????12=4,
解得:????1=3,????2=?1;
(2)????2?6?????18=0
∴????2?6????=18,
∴????2?6????+9=27,
即?????32=27,
∴?????3=±33,
解得:????1=3+33,????2=3?33;
(3)3?????22=?????????2
∴3?????22??????????2=0,
∴?????22?????6=0,
解得:????1=2,????2=3;
?
1解方程:
(1)?????12=4
(2)????2?6?????18=0
(3)3?????22=?????????2
?
针对训练
考点三 解一元二次方程
2.下列方程中,适合用直接开方法解的个数有( )
① 13x2=1;②(x﹣2)2=5;③14(x+3)2=3;④x2=x+3;⑤3x2﹣3=x2+1;
⑥y2﹣2y﹣3=0
A.1 B.2 C.3 D.4
3.用配方法解方程x2﹣23x﹣1=0时,应将其变形为( )
A.(x﹣13)2=89 B.(x+13)2=109????C.(x﹣23)2=0 D.(x﹣13)2=109
?
针对训练
考点三 解一元二次方程
4.下列一元二次方程最适合用分解因式法解的是( )
A.(x-1)(x-2)=3 B.x2 +4x=23
C.x2+2x-1=0 D.(x-3)2=x2-9
5.已知x、y都是实数,且(x2+y2)(x2+y2+2)﹣3=0,那么x2+y2的值是( )
A.﹣3 B.1 C.﹣3或1 D.﹣1或3
知识大全
考点四 一元二次方程根的判别式
一般地,式子b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式。
判别式概念:
判别式表示:
通常用希腊字母“Δ”表示,即Δ=b2-4ac.
(x+b2a)2=b2?4ac4a2=Δ4a2
?
由前面的推导过程,可知:
1)若△>0,一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实根。
2)若△= 0,一元二次方程ax2+bx+c=0(a≠0)有两个 相等的实根。
3)若△<0,一元二次方程ax2+bx+c=0(a≠0) 无 实根。
即当Δ≥0时,方程ax2+bx+c=0(a≠0)的实数根为
解题技巧
考点四 一元二次方程根的判别式
一元二次方程????????2+????????+????=0(????≠0) 根的判别式:????=????2?4????????
1)????>0?方程有两个不相等的实根:????=?????±????2?4????????2????(????2?4????????≥0)
2)????=0?方程有两个相等的实根:????1=????2=?????2????
3)??<0?方程无实根
【选择题快速判断法】如果a、c异号,所以ac<0,则????>0,方程有两个不相等的实根.
?
针对训练
考点四 一元二次方程根的判别式
【典例5】关于????的一元二次方程????2?????+3????+2????+1=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.有两个实数根 D.没有实数根
1.已知关于x的一元二次方程????2+2x?????=0有两个相等的实数根,则a的值是( )
A.4 B.﹣4 C.1 D.﹣1
2.方程(?????2)????2?4?????1=0有两个不等的实数根,则????的取值范围是( ).
A.????>??2 B.?????2且????≠2
?
针对训练
考点四 一元二次方程根的判别式
3. (青海省西宁市城区2022年中考数学真题)关于x的一元二次方程2x2+x?k=0没有实数根,则k的取值范围是(???????)
A.k?18 D.k≥?18
4.(2022年甘肃省兰州市中考数学真题)关于x的一元二次方程kx2+2x?1=0有两个相等的实数根,则k=(???????)
A.-2 B.-1 C.0 D.1
?
【详解】解:∵一元二次方程2????2+?????????=0没有实数根,
∴Δ=12?4×2×(?k)<0,解得?????
【详解】
∵原方程有两个相等的实数根,
∴△=b2?4ac=4?4×(?k)=0,且k≠0;
解得????=?1.
故选:B.
?
知识大全
考点五 一元二次方程根与系数的关系
当Δ?≥0时,两根的和等于一次项系数与二次项系数的___________,
两根的积等于常数项与二次项系数的___________,
即方程ax2+bx+c=0(a≠0),根与系数的关系为:
人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”。
?
【易错点】使用韦达定理的前提条件:1) 先把方程化为一般式。
2) Δ≥0。
比的相反数
比
x1+x2 =?ba, x1x2 = ca
?
解题技巧
考点五 一元二次方程根与系数的关系
已知一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2
1)平方和 ????????????+????????????=
2)倒数和 ???????????? + ????????????? =
3)差的绝对值 | x1 - x2 |=
4)????1????2+????2????1 =
5)(????1+1)(????2+1)=
?
(????????+????????)?????????????????????????
?
????????+????????????????????????
?
(?????????????????)????=(????????+????????)?????????????????????????
?
????12+????22????1????2=(????1+????2)2?2????1????2????1????2
?
????1????2+(????1+????2)+1
?
针对训练
考点五 一元二次方程根与系数的关系
【典例6】已知关于x的一元二次方程????2+3????+?????2=0有实数根.
(1)求实数k的取值范围.
(2)设方程的两个实数根分别为????1,????2,若????1+1????2+1=?1,求k的值.
?
【详解】(1)解:∵一元二次方程????2+3????+?????2=0有实数根.
∴?≥0,即32-4(k-2)≥0, 解得k≤174
(2)∵方程的两个实数根分别为????1,????2,
∴????1+????2=?3,????1????2=?????2,
∵????1+1????2+1=?1,
∴????1????2+????1+????2+1=?1,
∴?????2?3+1=?1,
解得k=3.
?
针对训练
考点五 一元二次方程根与系数的关系
1.已知关于x的一元二次方程????2?4?????2????+8=0有两个实数根????1,????2.
(1)求k的取值范围;
(2)若????13????2+????1????23=24,求k的值.
?
【详解】解:(1)由题意可知,????=(?4)2?4×1×(?2????+8)≥0,
整理得:16+8?????32≥0,
解得:????≥2,
∴????的取值范围是:????≥2.
故答案为:????≥2.
?
针对训练
考点五 一元二次方程根与系数的关系
2.已知关于x的一元二次方程????2?4?????2????+8=0有两个实数根????1,????2.
(1)求k的取值范围;
(2)若????13????2+????1????23=24,求k的值.
?
(2)由题意得:????13????2+????1????23=????1????2(????1+????2)2?2????1????2=24,
由韦达定理可知:????1+????2=4,????1????2=?2????+8,
故有:(?2????+8)42?2(?2????+8)=24,
整理得:????2?4????+3=0,
解得:????1=3,????2=1,
又由(1)中可知????≥2,
∴????的值为????=3.
故答案为:????=3.
?
针对训练
考点五 一元二次方程根与系数的关系
3.(2022年湖北省十堰市中考数学真题)已知关于????的一元二次方程????2?2?????3????2=0.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根分别为????,????,且????+2????=5,求????的值.
?
【解析】
(1)Δ=????2?4????????=?22?4×1?(?3????2)=4+12????2,
∵12????2≥0,∴4+12????2≥4>0,∴该方程总有两个不相等的实数根;
(2)∵方程的两个实数根????,????,由根与系数关系可知,????+????=2,?????????=?3????2,
∵????+2????=5,∴????=5?2????,
∴5?2????+????=2,解得:????=3,????=?1,
∴?3????2=?1×3=?3,
即????=±1.
?
解题技巧
考点六 利用一元二次方程解决实际问题
利用一元二次方程解决实际问题:
1)传播问题:明确每轮传播中的___________个数,以及这一轮被传染的__________.
2) 增长率问题:
①如果增长率问题中的基数为a,平均增长率为x,则第一次增长后的数量为
____________,第二次增长后的数量为____________.
②如果下降率问题中的基数为a,平均下降率为x,则第一次下降后的数量为
__________,第二次下降后的数量为___________.
3)几何问题:
①常见几何____________是等量关系。
②解决课本封面、小路宽度常采用____________列方程。
传染源
总数
a(1+x)
a(1+x)2
a(1-x)
a(1-x)2
周长面积
图形平移
解题技巧
考点六 利用一元二次方程解决实际问题
利用一元二次方程解决实际问题:
4) 数字问题:
①若个位数字为a,十位数字为b,百位数字为c,则十位数字表示为____________.
百位数字表示_____________.
②日历中的某个日期,左右相差___________,上下相差___________.
5)利润问题:单件利润=___________,总利润=________________
6) 表格问题:理解题干内容,从题干中获取信息。
7)动点问题:在动点中观察图形的变化情况,需理解动点在图形不同位置情况,才
能做好计算推理过程。在变化中找到不变的性质是解决动点问题的基本思路。
100c+10b+a
10b+a
1
7
售价-进价
单件利润×销量
针对训练
考点六 利用一元二次方程解决实际问题
1.“新冠肺炎”防治取得战略性成果.若有一个人患了“新冠肺炎”,经过两轮传染后共有25个人患了“新冠肺炎”,则每轮传染中平均一个人传染了_________人.
【详解】设每轮传染中平均一个人传染了x人,则第一轮传染中有x人被传染,第二轮传染中有????(1+????)人被传染,由题意得 1+????+????(1+????)=25
解得????=4或?6(舍去)所以,每轮传染中平均一个人传染了4人,故答案为:4.
?
【详解】设十位上的数字为x,则个位上的数字为(x﹣4).
可列方程为:x2+(x﹣4)2=10x+(x﹣4)﹣4
解得:x1=8,x2=1.5(舍),∴x﹣4=4,
∴10x+(x﹣4)=84.
答:这个两位数为84.故答案为:84
2.已知一个两位数,个位上的数字比十位上的数字小4,且个位上的数字与十位上的数字的平方和比这个两位数小4,则这个两位数是___.
针对训练
考点六 利用一元二次方程解决实际问题
【详解】解:由题意得:
50?????300+10????=16000;
故答案为50?????300+10????=16000.
?
3.2021年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价????元,可列方程________.
?
针对训练
考点六 利用一元二次方程解决实际问题
4.已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于210cm?
(3)△PQB的面积能否等于7 平方厘米?请说明理由.
?
【提示】(1)设P、Q分别从A、B两点出发,x秒后,AP=xcm,PB=(5-x)cm,BQ=2xcm,则△PBQ的面积等于12×2x(5-x),令该式等于4,列出方程求出符合题意的解;
(2)利用勾股定理列出方程求解即可;
(3)看△PBQ的面积能否等于7cm2,只需令12×2t(5-t)=7,化简该方程后,判断该方程的????2?4????????与0的关系,大于或等于0则可以,否则不可以.
?
谢谢!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
