4.1 从问题到方程 课件(共31张PPT)-2023-2024学年七年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 4.1 从问题到方程 课件(共31张PPT)-2023-2024学年七年级数学上册同步精品课堂(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 44.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 21:48:42 | ||
图片预览











文档简介
4.1 从问题到方程
第4章 代数式
教学目标
01
在探索实际问题中的已知量与未知量之间的等量关系过程中,
认识用方程描述等量关系的简明性
02
理解等式与方程的概念,初步构建起方程的框架体系
03
理解整式方程与一元一次方程的概念,能准确识别出一元一次方程
等式与方程
知识精讲
法律天平象征着公平与正义
天平是一种比较有形物体重量差异的仪器,如果两边重量稍有不等,就会偏斜;法院是对无形行为评判、对是非明辨的部门,要求公正不阿,如果有私心或被权力金钱所左右,也就会让庄严的法律失去平衡。
由于以天平作为公正的标识,那么在审理案件时,法官就能很好地运用天平原理操作了。在现行的法律天平中,法官普遍运用了天平原理进行权衡,且确保了其准确性,两边孰轻孰重,法律的天平一下子就获得了结果,也让旁人一看就明白谁是谁非。
01
情境引入
知识精讲
Q1:如图,天平右边放了2只水蜜桃,共250g,左边放了1只100g的橘子和2只质量相等的苹果,此时天平平衡。如何描述其中的等量关系?
01
情境引入
【分析】等量关系:
2只苹果的质量+100g=2×250g
设一只苹果的质量为xg,
则2x+100=2×250
知识精讲
Q2:篮球联赛规则规定:胜一场得2分,负一场得1分。某篮球队赛了12场,共得20分,如何描述其中的等量关系?
设未知数,可以简化已知量和未知量之间的等量关系~
01
情境引入
【分析】等量关系:
胜场得分+负场得分=20分
设该队胜x场,则该队负(12-x)场,
则2x+(12-x)=20
知识精讲
Q3:《百僧百馒》
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁?
翻译:100个馒头,100个和尚,大和尚1人分了3个馒头,小和尚3人分了1个馒头,大、小和尚各有多少人?
我饿!
我饱!
01
情境引入
【分析】等量关系:
大和尚分到的馒头数+小和尚分到的馒头数=100个
如果设大和尚有x人,则小和尚有(100-x)人,
则3x+?????????????????????=100
?
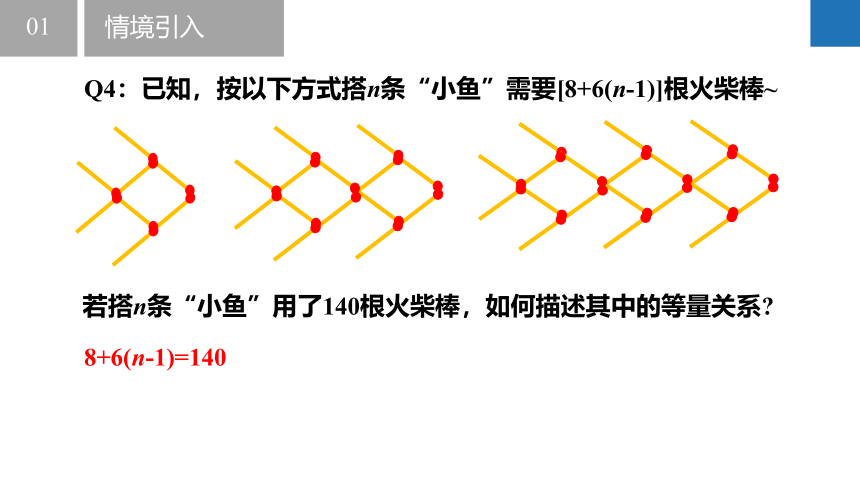
Q4:已知,按以下方式搭n条“小鱼”需要[8+6(n-1)]根火柴棒~
若搭n条“小鱼”用了140根火柴棒,如何描述其中的等量关系?
8+6(n-1)=140
01
情境引入
知识精讲
01
情境引入
Q5:小红今年5岁,爸爸32岁,如果x年后小红的年龄是爸爸年龄的????????,如何描述其中的等量关系?
?
【分析】等量关系:
小红的年龄=爸爸年龄×????????
?
x年后小红(5+x)岁,
则5+x=????????(32+x)
?
观察这几个式子,找出它们的共同点:
2x+100=500
2x+(12-x)=20
3x+?????????????????????=100
8+6(n-1)=140
5+x=????????(32+x)
?
(1)都是由等号连接的式子
(2)每个式子都含有未知数
02
知识精讲
等式
等式
注意:
(1)单项式、多项式等代数式也不是等式;
(2)含有“>”“<”“≥”“≤”“≠”“≈”等符号的式子不是等式。
02
知识精讲
等式的定义:
用“ = ”连接,表示相等关系的式子,叫做等式。
等号左右两边的式子,分别叫做这个等式的左边、右边。
例1、(1)判断下列各式中,属于等式的是( )
A. x+y≠7 B. x<2 C. x+2x=3x D. x2+y2
(2)下列各式中,哪些是等式________(填序号)。
①m+2=n ②x-y ③4>2 ④a+b=1 ⑤x>y
C
①④
03
典例精析
总结:
看是否有等号即可
拓展——等式的分类
02
知识精讲
等式的分类:
(1)像1+1=2,5=5,2x+3x=5x这样,一定成立的等式叫做恒等式;
(2)像x=2,a=????????,x2=4这样,在某些条件下成立的等式叫做条件等式;
?
(3)像1+1=3,x-1=x+1这样,一定不可能成立的等式叫做矛盾等式。
例2、(1)????????????????=????????????????,(2)2-3=4,(3)2x-3x=4x,(4)x2+y2=0,(5)|x|=-1这五个等式中,属于恒等式的有__________;属于条件等式的有__________;属于矛盾等式的有__________。
?
【分析】(1)????????????????=????????=????????????????,为恒等式
?
(2)2-3=4,一定不可能成立,为矛盾等式
(3)当且仅当x=0时成立,为条件等式
(4)当且仅当x=0,y=0时成立,为条件等式
(5)|x|=-1,一定不可能成立,为矛盾等式
(1)
(2)(5)
(3)(4)
03
典例精析
2x+100=500
2x+(12-x)=20
3x+?????????????????????=100
8+6(n-1)=140
5+x=????????(32+x)
?
(1)都是由等号连接的式子
(2)每个式子都含有未知数
02
知识精讲
等式
方程
方程的定义:
含有未知数的等式叫做方程。
注意:
(1)方程一定等式;
(2)方程中必须含有未知数。
方程
02
知识精讲
例3、下列各式中,哪些是方程:__________。
(1)5x-2y
(2)4-2=0
(3)4x>6
(4)x+3=????????
(5)2x-8y=3x-1
?
(4)(5)
×不是等式
×不含未知数
×不是等式
是等式+含有未知数,是方程
03
典例精析
是等式+含有未知数,是方程
方程中的未知数可以不止一个
一元一次方程
知识精讲
我们知道,代数式分为整式和分式,那么方程又是如何分类的呢?
01
情境引入
类似地,方程分为整式方程与分式方程,而整式方程就是我们现阶段要学习的内容。
观察例3中的方程“x+3=????????”,方程的分母中含有未知数,这样的方程就叫做分式方程(八下)。
?
整式方程的定义:
方程左右两边都是整式,称之为整式方程。
注意:
(1)类似于整式中的概念,方程中所含未知数的个数,称为方程的元数;
(2)化简后方程中含未知数项的最高次数,称为方程的次数。
02
知识精讲
整式方程
继续观察这几个方程,找出它们的共同点:
【提示:从方程的分类,元数,次数来考虑】
2x+100=500
2x+(12-x)=20
3x+?????????????????????=100
8+6(n-1)=140
5+x=????????(32+x)
?
02
知识精讲
(2)都只含有一个未知数
(3)且未知数的次数都是1
(1)都是整式方程
一元一次方程
方程的概念
一元一次方程
02
知识精讲
一元一次方程的定义:
只含有一个未知数,且未知数的次数都是1,
这样的整式方程叫做一元一次方程。
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
方程的概念
一元一次方程的概念
判断以下方程是否为一元一次方程:
(1)x+y=1
(2)x2+2=3
(3)????????=-1
?
×,有两个未知数
×,未知数次数是2
×,分母中含有未知数,是分式方程
02
知识精讲
总结:
紧抓三要素
方程的概念
一元一次方程的概念
拓展
x2+x=x2是否为一元一次方程?
口诀:
元看化简前,
次看化简后
02
知识精讲
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
化简得x=0
方程的概念
一元一次方程的概念
拓展
3x+y=y是否为一元一次方程?
02
知识精讲
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
元看化简前——两个未知数
方程的概念
一元一次方程的概念
拓展
x+5=x是否为一元一次方程?
02
知识精讲
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
元看化简前
次看化简后——化简得5=0
例1、已知下列方程:
(1)x-2=????????;(2)0.3x=1;(3)????????=5x+1;(4)x2-4x=3;(5)x=6;(6)x+2y=0
其中一元一次方程的个数是( )
A. 2 B. 3 C. 4 D. 5
?
(4)×,未知数的次数不全是1
(6)×,有两个未知数
B
03
典例精析
【分析】(1)×,分母中含有未知数,是分式方程
【分析】(1)2k-1=1,解得:k=1;
例2、根据一元二次方程的定义求参:
(1)若关于x的方程x2k-1+8=0是一元一次方程,则k=________;
(2)若关于x的方程(k-1)x+3=0是一元一次方程,则k=________;
(3)若关于x的方程(k-2)x|k|-1+5=0是一元一次方程,则k=________。
1
(2)k-1≠0,解得:k≠1;
≠1
(3)|k|-1=1且k-2≠0,∴k=-2。
-2
03
典例精析
【总结】
若关于x的方程axm+b=0是一元一次方程,则________________。
03
典例精析
m=1且a≠0
课后总结
等式的定义:
用“ = ”连接,表示相等关系的式子,叫做等式。
等号左右两边的式子,分别叫做这个等式的左边、右边。
注意:
(1)单项式、多项式等代数式也不是等式;
(2)含有“>”“<”“≥”“≤”“≠”“≈”等符号的式子不是等式。
方程的定义:
含有未知数的等式叫做方程。
注意:
(1)方程一定等式;
(2)方程中必须含有未知数。
等式的分类:
(1)像1+1=2,5=5,2x+3x=5x这样,一定成立的等式叫做恒等式;
(2)像x=2,a=????????,x2=4这样,在某些条件下成立的等式叫做条件等式;
(3)像1+1=3,x-1=x+1这样,一定不可能成立的等式叫做矛盾等式。
?
课后总结
整式方程的定义:
方程左右两边都是整式,称之为整式方程。
注意:
(1)类似于整式中的概念,方程中所含未知数的个数,称为方程的元数;
(2)化简后方程中含未知数项的最高次数,称为方程的次数。
一元一次方程的定义:
只含有一个未知数,且未知数的次数都是1,
这样的整式方程叫做一元一次方程。
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
第4章 代数式
教学目标
01
在探索实际问题中的已知量与未知量之间的等量关系过程中,
认识用方程描述等量关系的简明性
02
理解等式与方程的概念,初步构建起方程的框架体系
03
理解整式方程与一元一次方程的概念,能准确识别出一元一次方程
等式与方程
知识精讲
法律天平象征着公平与正义
天平是一种比较有形物体重量差异的仪器,如果两边重量稍有不等,就会偏斜;法院是对无形行为评判、对是非明辨的部门,要求公正不阿,如果有私心或被权力金钱所左右,也就会让庄严的法律失去平衡。
由于以天平作为公正的标识,那么在审理案件时,法官就能很好地运用天平原理操作了。在现行的法律天平中,法官普遍运用了天平原理进行权衡,且确保了其准确性,两边孰轻孰重,法律的天平一下子就获得了结果,也让旁人一看就明白谁是谁非。
01
情境引入
知识精讲
Q1:如图,天平右边放了2只水蜜桃,共250g,左边放了1只100g的橘子和2只质量相等的苹果,此时天平平衡。如何描述其中的等量关系?
01
情境引入
【分析】等量关系:
2只苹果的质量+100g=2×250g
设一只苹果的质量为xg,
则2x+100=2×250
知识精讲
Q2:篮球联赛规则规定:胜一场得2分,负一场得1分。某篮球队赛了12场,共得20分,如何描述其中的等量关系?
设未知数,可以简化已知量和未知量之间的等量关系~
01
情境引入
【分析】等量关系:
胜场得分+负场得分=20分
设该队胜x场,则该队负(12-x)场,
则2x+(12-x)=20
知识精讲
Q3:《百僧百馒》
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁?
翻译:100个馒头,100个和尚,大和尚1人分了3个馒头,小和尚3人分了1个馒头,大、小和尚各有多少人?
我饿!
我饱!
01
情境引入
【分析】等量关系:
大和尚分到的馒头数+小和尚分到的馒头数=100个
如果设大和尚有x人,则小和尚有(100-x)人,
则3x+?????????????????????=100
?
Q4:已知,按以下方式搭n条“小鱼”需要[8+6(n-1)]根火柴棒~
若搭n条“小鱼”用了140根火柴棒,如何描述其中的等量关系?
8+6(n-1)=140
01
情境引入
知识精讲
01
情境引入
Q5:小红今年5岁,爸爸32岁,如果x年后小红的年龄是爸爸年龄的????????,如何描述其中的等量关系?
?
【分析】等量关系:
小红的年龄=爸爸年龄×????????
?
x年后小红(5+x)岁,
则5+x=????????(32+x)
?
观察这几个式子,找出它们的共同点:
2x+100=500
2x+(12-x)=20
3x+?????????????????????=100
8+6(n-1)=140
5+x=????????(32+x)
?
(1)都是由等号连接的式子
(2)每个式子都含有未知数
02
知识精讲
等式
等式
注意:
(1)单项式、多项式等代数式也不是等式;
(2)含有“>”“<”“≥”“≤”“≠”“≈”等符号的式子不是等式。
02
知识精讲
等式的定义:
用“ = ”连接,表示相等关系的式子,叫做等式。
等号左右两边的式子,分别叫做这个等式的左边、右边。
例1、(1)判断下列各式中,属于等式的是( )
A. x+y≠7 B. x<2 C. x+2x=3x D. x2+y2
(2)下列各式中,哪些是等式________(填序号)。
①m+2=n ②x-y ③4>2 ④a+b=1 ⑤x>y
C
①④
03
典例精析
总结:
看是否有等号即可
拓展——等式的分类
02
知识精讲
等式的分类:
(1)像1+1=2,5=5,2x+3x=5x这样,一定成立的等式叫做恒等式;
(2)像x=2,a=????????,x2=4这样,在某些条件下成立的等式叫做条件等式;
?
(3)像1+1=3,x-1=x+1这样,一定不可能成立的等式叫做矛盾等式。
例2、(1)????????????????=????????????????,(2)2-3=4,(3)2x-3x=4x,(4)x2+y2=0,(5)|x|=-1这五个等式中,属于恒等式的有__________;属于条件等式的有__________;属于矛盾等式的有__________。
?
【分析】(1)????????????????=????????=????????????????,为恒等式
?
(2)2-3=4,一定不可能成立,为矛盾等式
(3)当且仅当x=0时成立,为条件等式
(4)当且仅当x=0,y=0时成立,为条件等式
(5)|x|=-1,一定不可能成立,为矛盾等式
(1)
(2)(5)
(3)(4)
03
典例精析
2x+100=500
2x+(12-x)=20
3x+?????????????????????=100
8+6(n-1)=140
5+x=????????(32+x)
?
(1)都是由等号连接的式子
(2)每个式子都含有未知数
02
知识精讲
等式
方程
方程的定义:
含有未知数的等式叫做方程。
注意:
(1)方程一定等式;
(2)方程中必须含有未知数。
方程
02
知识精讲
例3、下列各式中,哪些是方程:__________。
(1)5x-2y
(2)4-2=0
(3)4x>6
(4)x+3=????????
(5)2x-8y=3x-1
?
(4)(5)
×不是等式
×不含未知数
×不是等式
是等式+含有未知数,是方程
03
典例精析
是等式+含有未知数,是方程
方程中的未知数可以不止一个
一元一次方程
知识精讲
我们知道,代数式分为整式和分式,那么方程又是如何分类的呢?
01
情境引入
类似地,方程分为整式方程与分式方程,而整式方程就是我们现阶段要学习的内容。
观察例3中的方程“x+3=????????”,方程的分母中含有未知数,这样的方程就叫做分式方程(八下)。
?
整式方程的定义:
方程左右两边都是整式,称之为整式方程。
注意:
(1)类似于整式中的概念,方程中所含未知数的个数,称为方程的元数;
(2)化简后方程中含未知数项的最高次数,称为方程的次数。
02
知识精讲
整式方程
继续观察这几个方程,找出它们的共同点:
【提示:从方程的分类,元数,次数来考虑】
2x+100=500
2x+(12-x)=20
3x+?????????????????????=100
8+6(n-1)=140
5+x=????????(32+x)
?
02
知识精讲
(2)都只含有一个未知数
(3)且未知数的次数都是1
(1)都是整式方程
一元一次方程
方程的概念
一元一次方程
02
知识精讲
一元一次方程的定义:
只含有一个未知数,且未知数的次数都是1,
这样的整式方程叫做一元一次方程。
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
方程的概念
一元一次方程的概念
判断以下方程是否为一元一次方程:
(1)x+y=1
(2)x2+2=3
(3)????????=-1
?
×,有两个未知数
×,未知数次数是2
×,分母中含有未知数,是分式方程
02
知识精讲
总结:
紧抓三要素
方程的概念
一元一次方程的概念
拓展
x2+x=x2是否为一元一次方程?
口诀:
元看化简前,
次看化简后
02
知识精讲
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
化简得x=0
方程的概念
一元一次方程的概念
拓展
3x+y=y是否为一元一次方程?
02
知识精讲
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
元看化简前——两个未知数
方程的概念
一元一次方程的概念
拓展
x+5=x是否为一元一次方程?
02
知识精讲
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
元看化简前
次看化简后——化简得5=0
例1、已知下列方程:
(1)x-2=????????;(2)0.3x=1;(3)????????=5x+1;(4)x2-4x=3;(5)x=6;(6)x+2y=0
其中一元一次方程的个数是( )
A. 2 B. 3 C. 4 D. 5
?
(4)×,未知数的次数不全是1
(6)×,有两个未知数
B
03
典例精析
【分析】(1)×,分母中含有未知数,是分式方程
【分析】(1)2k-1=1,解得:k=1;
例2、根据一元二次方程的定义求参:
(1)若关于x的方程x2k-1+8=0是一元一次方程,则k=________;
(2)若关于x的方程(k-1)x+3=0是一元一次方程,则k=________;
(3)若关于x的方程(k-2)x|k|-1+5=0是一元一次方程,则k=________。
1
(2)k-1≠0,解得:k≠1;
≠1
(3)|k|-1=1且k-2≠0,∴k=-2。
-2
03
典例精析
【总结】
若关于x的方程axm+b=0是一元一次方程,则________________。
03
典例精析
m=1且a≠0
课后总结
等式的定义:
用“ = ”连接,表示相等关系的式子,叫做等式。
等号左右两边的式子,分别叫做这个等式的左边、右边。
注意:
(1)单项式、多项式等代数式也不是等式;
(2)含有“>”“<”“≥”“≤”“≠”“≈”等符号的式子不是等式。
方程的定义:
含有未知数的等式叫做方程。
注意:
(1)方程一定等式;
(2)方程中必须含有未知数。
等式的分类:
(1)像1+1=2,5=5,2x+3x=5x这样,一定成立的等式叫做恒等式;
(2)像x=2,a=????????,x2=4这样,在某些条件下成立的等式叫做条件等式;
(3)像1+1=3,x-1=x+1这样,一定不可能成立的等式叫做矛盾等式。
?
课后总结
整式方程的定义:
方程左右两边都是整式,称之为整式方程。
注意:
(1)类似于整式中的概念,方程中所含未知数的个数,称为方程的元数;
(2)化简后方程中含未知数项的最高次数,称为方程的次数。
一元一次方程的定义:
只含有一个未知数,且未知数的次数都是1,
这样的整式方程叫做一元一次方程。
三要素:
(1)整式方程;
(2)一元:一个未知数;
(3)一次:化简后未知数的次数是1。
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
