4.2.1 解一元一次方程-第1课时 课件(共29张ppt)-2023-2024学年七年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 4.2.1 解一元一次方程-第1课时 课件(共29张ppt)-2023-2024学年七年级数学上册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 21:46:01 | ||
图片预览







文档简介
(共29张PPT)
4.2.1 解一元一次方程-第1课时
第4章 代数式
教学目标
01
理解方程的解、解方程的概念,能验证方程的解的正确性
02
理解等式的性质,并灵活应用于解简单的一元一次方程
方程的解与解方程
过路人,这座石墓里安葬着丢番图。
他生命的1/6是幸福的童年,生命的1/12是青少年时期,又过了生命的1/7他才结婚。
婚后5年有了一个孩子,孩子活到他父亲一半的年纪便去世了,孩子去世后,丢番图在深深的悲哀中又活了4年,也结束了尘世生涯。
过路人,你知道丢番图的寿命吗?
设丢番图的寿命为x岁,请根据墓志铭,列方程~
01
情境引入Part1
如何求方程中x的值呢?
01
情境引入Part1
x+x+x+5+x+4=x
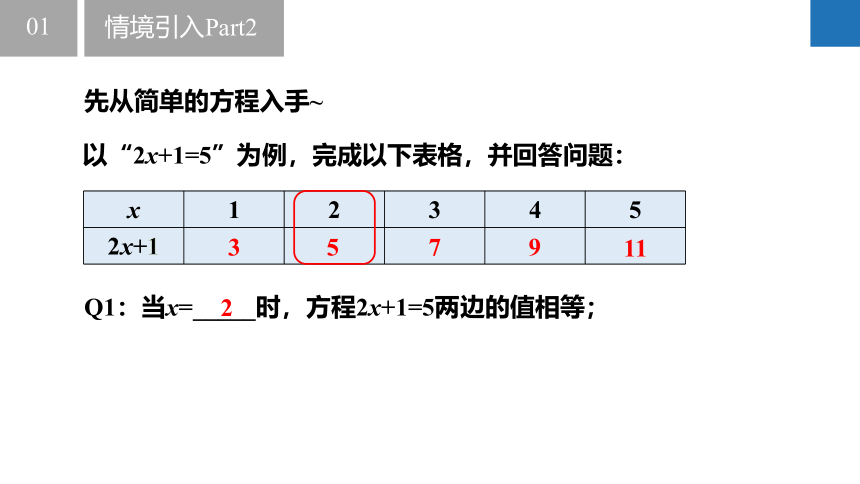
以“2x+1=5”为例,完成以下表格,并回答问题:
x 1 2 3 4 5
2x+1
Q1:当x=_____时,方程2x+1=5两边的值相等;
3
5
7
11
9
2
01
情境引入Part2
先从简单的方程入手~
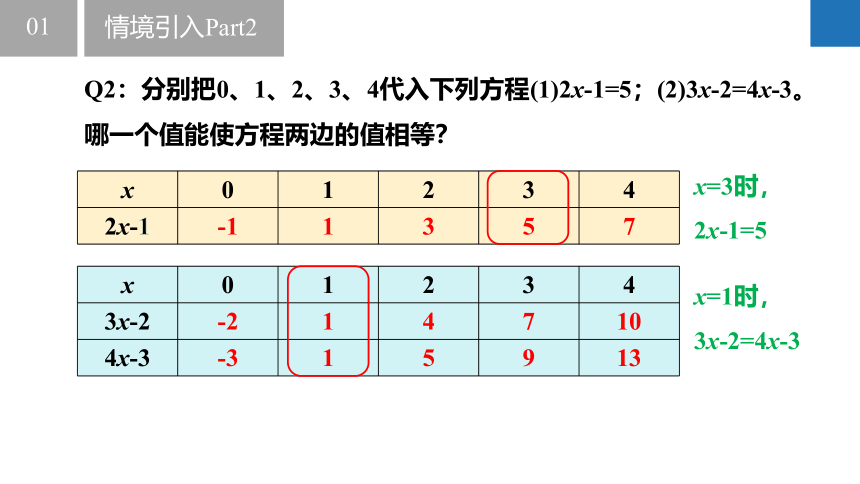
Q2:分别把0、1、2、3、4代入下列方程(1)2x-1=5;(2)3x-2=4x-3。哪一个值能使方程两边的值相等?
x 0 1 2 3 4
2x-1 -1 1 3 5 7
x=3时,
2x-1=5
01
情境引入Part2
x 0 1 2 3 4
3x-2 -2 1 4 7 10
4x-3 -3 1 5 9 13
x=1时,
3x-2=4x-3
方程的概念
02
知识精讲
方程的解
方程的解的定义:
使方程左、右两边相等的未知数的值,叫做方程的解。
注意:
(1)解的形式为“x= ”,如x=2是2x+1=5的解;
(2)对于只含有一个未知数的方程,它的解也叫方程的根。
方程的概念
02
知识精讲
解方程
解方程的定义:
求方程的解的过程,叫做解方程。
注意:
方程的解和解方程是两个不同的概念,
方程的解是指使方程两边相等的未知数的值,具有名词性;
而解方程是求方程解的过程,具有动词性。
例1、以下为方程3x+5=8的解的是( )
A. x=1 B. x=0 C. x=3 D. x=2
解题策略:
将未知数的值代入,看方程左右两边是否相等
A
03
典例精析
例2、已知x=3是关于x的方程2x-a=1的解,则a的值是________。
5
解题策略:
将未知数的值代入,根据方程左右两边相等求参
03
典例精析
等式的性质
方程的概念
方程的解
方程“2x+1=5”如何变形为“x=2”
2x+1=5
两边都减去1
2x=4
两边都乘以1/2或除以2
x
x
1
5
x
x
4
x
2
x=2
01
情境引入
方程的概念
方程的解
方程“2x-1=5”如何变形为“x=3”
2x-1=5
两边都加上1
2x=6
两边都乘以1/2或除以2
x
x
-1
5
x
x
6
x
3
x=3
01
情境引入
方程的概念
方程的解
方程“3x-2=4x-3”如何变形为“x=1”
3x-2=4x-3
两边都加上2,且减去4x
-x=-1
两边都乘以或除以-1
-x
-1
x
1
x=1
01
情境引入
x
x
-2
-3
x
x
x
x
x
根据以上三个变形,你发现等式具有怎样的性质?
方程的概念
等式的性质
若a=b,则a±c=b±c
若a=b,则ac=bc;若a=b(c≠0),则a/c=b/c
02
知识精讲
等式的性质1:
等式两边同时加上(或减去)同一个数(或式),等式仍然成立;
等式的性质2:
等式两边同时乘同一个数(或除以同一个不为0的数),等式仍然成立。
例1、根据等式的性质填空,并说明根据的是哪一条等式性质:
(1)x-4=4,则x=________,根据________________;
(2)2x=3-y,则x=________,根据________________;
(3)-x=3y,则x=________,根据________________。
8
等式性质1
等式性质2
等式性质2
03
典例精析
-
例2、(1) 如果x=y,那么下列等式不一定成立的是( )
A. x+a=y+a B. x-a=y-a C. ax=ay D. =
D
03
典例精析
【分析】
当a=0时,、无意义,条件里必须加上a≠0,D才对
例2、(2) 下列等式变形错误的是( )
A. 由a=b得a+5=b+5 B. 由a=b得=
C. 由=得a=b D. 由ax=ay得x=y
D
D. 当a=0时,x不一定等于y
03
典例精析
【分析】C. =,作为条件,已经默认了c≠0
解一元一次方程
进一步分析方程“2x+1=5”到“x=2”的变形~
01
情境引入
2x+1=5
两边都减去1:2x=5-1
2x=4
依据:__________
等式性质1
步骤名:__________
移项
移项的定义:
方程中的某些项改变符号后,可以从方程的一边移到另一边,这样的变形叫做移项。
步骤:
把方程右边的+1改变符号后,移到方程的左边
进一步分析方程“2x+1=5”到“x=2”的变形~
01
情境引入
2x+1=5
两边都减去1:2x=5-1
2x=4
依据:__________
等式性质2
两边都乘以1/2或除以2
x=2
步骤名:__________
系数化为1
目的:
使得含有未知数的项和不含未知数的项各在等式一边,以便合并同类项
操作:两边分别同时减x、减5、减4
易错:移项忘记变号
02
知识精讲
解方程:x+x+x+5+x+4=x
第一步:移项
x+x+x+x-x=-5-4
02
知识精讲
第二步:合并同类项
x+x+x+x-x=-5-4
-x=-9
第三步:系数化为1
x=84
操作:两边同时乘以-或除以-
解题小技巧
可利用方程的解的概念,将未知数的值带回到方程中去检验结果的正确性
解一元一次方程
注意:移项要变号
02
知识精讲
解一元一次方程的一般步骤:
1.移项;
2.合并同类项;
3.系数化为1。
例1、下列方程的变形属于正确移项的是( )
A. 由y-1=y+2,得y-y=2+1
B. 由x=-5+2x,得x=2x-5
C. 由2x-3=x+5,得2x+x=5-3
D. 由2=x,得6=7x
A
× 未移项
× 移项要变号!!!
× 未移项
03
典例精析
例2、解方程:
(1)3x+7=23-x (2)-7x-9=6x+4
解:(1)移项:3x+x=23-7
合并同类项:4x=16
系数化为1:x=4
(2)移项:-7x-6x=4+9
合并同类项:-13x=13
系数化为1:x=-1
03
典例精析
课后总结
方程的解的定义:
使方程左、右两边相等的未知数的值,叫做方程的解。
注意:
(1)解的形式为“x= ”,如x=2是2x+1=5的解;
(2)对于只含有一个未知数的方程,它的解也叫方程的根。
解方程的定义:
求方程的解的过程,叫做解方程。
注意:
方程的解和解方程是两个不同的概念,
方程的解是指使方程两边相等的未知数的值,具有名词性;
而解方程是求方程解的过程,具有动词性。
课后总结
等式的性质1:
等式两边同时加上(或减去)同一个数(或式),等式仍然成立;
若a=b,则a±c=b±c
等式的性质2:
等式两边同时乘同一个数(或除以同一个不为0的数),等式仍然成立。
若a=b,则ac=bc;若a=b(c≠0),则a/c=b/c
解一元一次方程的一般步骤:
1.移项;2.合并同类项;3.系数化为1。
注意:移项要变号
4.2.1 解一元一次方程-第1课时
第4章 代数式
教学目标
01
理解方程的解、解方程的概念,能验证方程的解的正确性
02
理解等式的性质,并灵活应用于解简单的一元一次方程
方程的解与解方程
过路人,这座石墓里安葬着丢番图。
他生命的1/6是幸福的童年,生命的1/12是青少年时期,又过了生命的1/7他才结婚。
婚后5年有了一个孩子,孩子活到他父亲一半的年纪便去世了,孩子去世后,丢番图在深深的悲哀中又活了4年,也结束了尘世生涯。
过路人,你知道丢番图的寿命吗?
设丢番图的寿命为x岁,请根据墓志铭,列方程~
01
情境引入Part1
如何求方程中x的值呢?
01
情境引入Part1
x+x+x+5+x+4=x
以“2x+1=5”为例,完成以下表格,并回答问题:
x 1 2 3 4 5
2x+1
Q1:当x=_____时,方程2x+1=5两边的值相等;
3
5
7
11
9
2
01
情境引入Part2
先从简单的方程入手~
Q2:分别把0、1、2、3、4代入下列方程(1)2x-1=5;(2)3x-2=4x-3。哪一个值能使方程两边的值相等?
x 0 1 2 3 4
2x-1 -1 1 3 5 7
x=3时,
2x-1=5
01
情境引入Part2
x 0 1 2 3 4
3x-2 -2 1 4 7 10
4x-3 -3 1 5 9 13
x=1时,
3x-2=4x-3
方程的概念
02
知识精讲
方程的解
方程的解的定义:
使方程左、右两边相等的未知数的值,叫做方程的解。
注意:
(1)解的形式为“x= ”,如x=2是2x+1=5的解;
(2)对于只含有一个未知数的方程,它的解也叫方程的根。
方程的概念
02
知识精讲
解方程
解方程的定义:
求方程的解的过程,叫做解方程。
注意:
方程的解和解方程是两个不同的概念,
方程的解是指使方程两边相等的未知数的值,具有名词性;
而解方程是求方程解的过程,具有动词性。
例1、以下为方程3x+5=8的解的是( )
A. x=1 B. x=0 C. x=3 D. x=2
解题策略:
将未知数的值代入,看方程左右两边是否相等
A
03
典例精析
例2、已知x=3是关于x的方程2x-a=1的解,则a的值是________。
5
解题策略:
将未知数的值代入,根据方程左右两边相等求参
03
典例精析
等式的性质
方程的概念
方程的解
方程“2x+1=5”如何变形为“x=2”
2x+1=5
两边都减去1
2x=4
两边都乘以1/2或除以2
x
x
1
5
x
x
4
x
2
x=2
01
情境引入
方程的概念
方程的解
方程“2x-1=5”如何变形为“x=3”
2x-1=5
两边都加上1
2x=6
两边都乘以1/2或除以2
x
x
-1
5
x
x
6
x
3
x=3
01
情境引入
方程的概念
方程的解
方程“3x-2=4x-3”如何变形为“x=1”
3x-2=4x-3
两边都加上2,且减去4x
-x=-1
两边都乘以或除以-1
-x
-1
x
1
x=1
01
情境引入
x
x
-2
-3
x
x
x
x
x
根据以上三个变形,你发现等式具有怎样的性质?
方程的概念
等式的性质
若a=b,则a±c=b±c
若a=b,则ac=bc;若a=b(c≠0),则a/c=b/c
02
知识精讲
等式的性质1:
等式两边同时加上(或减去)同一个数(或式),等式仍然成立;
等式的性质2:
等式两边同时乘同一个数(或除以同一个不为0的数),等式仍然成立。
例1、根据等式的性质填空,并说明根据的是哪一条等式性质:
(1)x-4=4,则x=________,根据________________;
(2)2x=3-y,则x=________,根据________________;
(3)-x=3y,则x=________,根据________________。
8
等式性质1
等式性质2
等式性质2
03
典例精析
-
例2、(1) 如果x=y,那么下列等式不一定成立的是( )
A. x+a=y+a B. x-a=y-a C. ax=ay D. =
D
03
典例精析
【分析】
当a=0时,、无意义,条件里必须加上a≠0,D才对
例2、(2) 下列等式变形错误的是( )
A. 由a=b得a+5=b+5 B. 由a=b得=
C. 由=得a=b D. 由ax=ay得x=y
D
D. 当a=0时,x不一定等于y
03
典例精析
【分析】C. =,作为条件,已经默认了c≠0
解一元一次方程
进一步分析方程“2x+1=5”到“x=2”的变形~
01
情境引入
2x+1=5
两边都减去1:2x=5-1
2x=4
依据:__________
等式性质1
步骤名:__________
移项
移项的定义:
方程中的某些项改变符号后,可以从方程的一边移到另一边,这样的变形叫做移项。
步骤:
把方程右边的+1改变符号后,移到方程的左边
进一步分析方程“2x+1=5”到“x=2”的变形~
01
情境引入
2x+1=5
两边都减去1:2x=5-1
2x=4
依据:__________
等式性质2
两边都乘以1/2或除以2
x=2
步骤名:__________
系数化为1
目的:
使得含有未知数的项和不含未知数的项各在等式一边,以便合并同类项
操作:两边分别同时减x、减5、减4
易错:移项忘记变号
02
知识精讲
解方程:x+x+x+5+x+4=x
第一步:移项
x+x+x+x-x=-5-4
02
知识精讲
第二步:合并同类项
x+x+x+x-x=-5-4
-x=-9
第三步:系数化为1
x=84
操作:两边同时乘以-或除以-
解题小技巧
可利用方程的解的概念,将未知数的值带回到方程中去检验结果的正确性
解一元一次方程
注意:移项要变号
02
知识精讲
解一元一次方程的一般步骤:
1.移项;
2.合并同类项;
3.系数化为1。
例1、下列方程的变形属于正确移项的是( )
A. 由y-1=y+2,得y-y=2+1
B. 由x=-5+2x,得x=2x-5
C. 由2x-3=x+5,得2x+x=5-3
D. 由2=x,得6=7x
A
× 未移项
× 移项要变号!!!
× 未移项
03
典例精析
例2、解方程:
(1)3x+7=23-x (2)-7x-9=6x+4
解:(1)移项:3x+x=23-7
合并同类项:4x=16
系数化为1:x=4
(2)移项:-7x-6x=4+9
合并同类项:-13x=13
系数化为1:x=-1
03
典例精析
课后总结
方程的解的定义:
使方程左、右两边相等的未知数的值,叫做方程的解。
注意:
(1)解的形式为“x= ”,如x=2是2x+1=5的解;
(2)对于只含有一个未知数的方程,它的解也叫方程的根。
解方程的定义:
求方程的解的过程,叫做解方程。
注意:
方程的解和解方程是两个不同的概念,
方程的解是指使方程两边相等的未知数的值,具有名词性;
而解方程是求方程解的过程,具有动词性。
课后总结
等式的性质1:
等式两边同时加上(或减去)同一个数(或式),等式仍然成立;
若a=b,则a±c=b±c
等式的性质2:
等式两边同时乘同一个数(或除以同一个不为0的数),等式仍然成立。
若a=b,则ac=bc;若a=b(c≠0),则a/c=b/c
解一元一次方程的一般步骤:
1.移项;2.合并同类项;3.系数化为1。
注意:移项要变号
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
