2023-2024学年人教版九年级数学上册24.4弧长和扇形面积 课件(共21张PPT)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册24.4弧长和扇形面积 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 515.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 16:13:09 | ||
图片预览


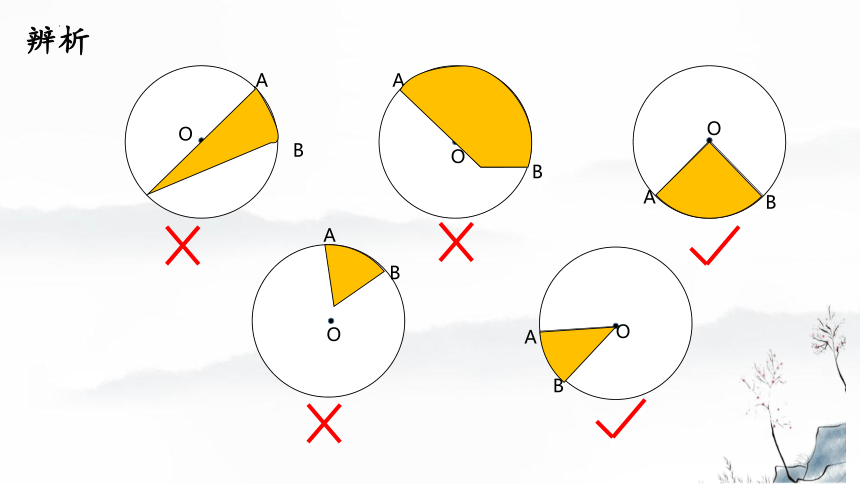




文档简介
(共21张PPT)
弧长和扇形面积
问题
空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,这头牛吃草的最大活动区域有多大?
O
A
B
1200
辨析
O
O
A
B
O
A
B
O
A
B
B
A
O
O
A
B
定义:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
扇 形
O
A
B
B
探究点一 扇形面积
扇形OAB
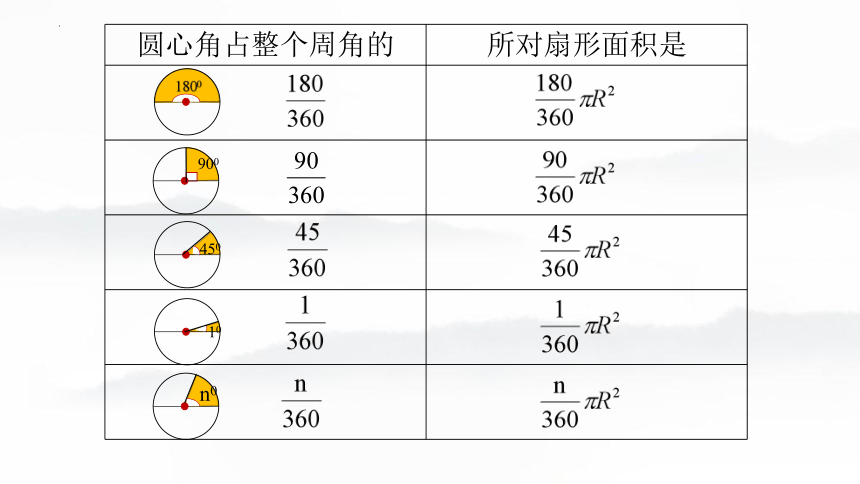
圆心角占整个周角的 所对扇形面积是
1800
900
450
10
n0
扇形面积公式
在半径为R的圆中,圆心角为n°的扇形面积是
注意:
1、 扇形面积与圆心角和半径的大小有关;
2、 n表示1°圆心角的倍数,它是不带单位的.
ooOOOOOOOO
结论
探究点二 弧长
O
A
B
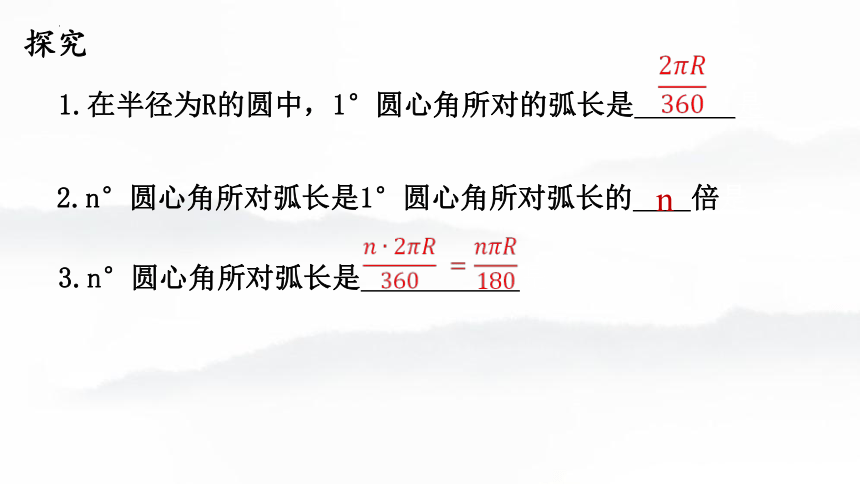
1.在半径为R的圆中,1°圆心角所对的弧长是 是
2.n°圆心角所对弧长是1°圆心角所对弧长的 倍是
n
3.n°圆心角所对弧长是 是
探究
O
C
B
D
A
弧长公式
半径为R, 圆心角为n°的弧长为
A
B
O
n°
1、弧长与圆心角和半径的大小有关;
2、n表示1°圆心角的倍数,它是不带单位的.
3、弧长相等的弧与等弧
注意:
结论
A
B
O
600
1.在半径为4的大⊙O中,AB所对的圆心
角为600 ,则弧长= s =
2.在半径为2的小⊙O中,CD所对的圆心角
是1200 ,则弧长= s
结论:弧长相等的弧不一定是等弧,
等弧的弧长相等.
练习
A
3.在半径为4的大⊙O中,EF所对的圆心角是600 ,则弧长= s =
1200
C
D
O
E
F
600
B
A
O
4.如图,在半径为4的⊙O中,AB长为 ,
则扇形的面积是 是
练习
600
想一想:扇形的面积公式
与什么公式类似?
探究点三 扇形的面积与弧长的关系公式
R
l
h
a
问题解决
空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,这头牛吃草的最大活动区域有多大?
O
B
A
1200
变式
如图,草地上有一根柱子,柱子两旁有两排栅栏,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,这头牛吃草的最大活动区域有多大?
A
D
B
C
O
解析:如图,大扇形的圆心角是90度,半径是5m,
所以面积是 ,小扇形
的圆心角是180°-120°=60°,半径是
1m,则面积= , ∴小牛A
在草地上的最大活动区域面积=
大扇形的圆心角是90度,大扇大扇形的圆心角是90度,形的圆心角是90度,
1200
O
B
900
C
A
1、已知扇形的圆心角是120°,半径为6,则扇形的弧长是( );
2、如图1所示,把边长为2的正方形ABCD的一边放在定直线l上,按顺时针方向绕D旋转
到如图的位置,则点B运
动到点B′所经过
的路线长度为( );
3、 如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为( )
当堂检测
2
A
D
B
B
L
C’
C
(A’)
A
D
B
B’
L
C’
4、如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是( )
当堂检测
小结
本节课你有什么收获?
公式:
思想: 类比+转化
“知之者不如好之者,好之者不如乐之者。” 兴趣是走向成功的原动力,保持浓厚的学习兴趣,你会享受到更多成功的乐趣。
老师寄语
作业
必做题 教科书 P115 1,2,3.
选做题 《基训》P112 11,12
谢 谢 !
弧长和扇形面积
问题
空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,这头牛吃草的最大活动区域有多大?
O
A
B
1200
辨析
O
O
A
B
O
A
B
O
A
B
B
A
O
O
A
B
定义:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
扇 形
O
A
B
B
探究点一 扇形面积
扇形OAB
圆心角占整个周角的 所对扇形面积是
1800
900
450
10
n0
扇形面积公式
在半径为R的圆中,圆心角为n°的扇形面积是
注意:
1、 扇形面积与圆心角和半径的大小有关;
2、 n表示1°圆心角的倍数,它是不带单位的.
ooOOOOOOOO
结论
探究点二 弧长
O
A
B
1.在半径为R的圆中,1°圆心角所对的弧长是 是
2.n°圆心角所对弧长是1°圆心角所对弧长的 倍是
n
3.n°圆心角所对弧长是 是
探究
O
C
B
D
A
弧长公式
半径为R, 圆心角为n°的弧长为
A
B
O
n°
1、弧长与圆心角和半径的大小有关;
2、n表示1°圆心角的倍数,它是不带单位的.
3、弧长相等的弧与等弧
注意:
结论
A
B
O
600
1.在半径为4的大⊙O中,AB所对的圆心
角为600 ,则弧长= s =
2.在半径为2的小⊙O中,CD所对的圆心角
是1200 ,则弧长= s
结论:弧长相等的弧不一定是等弧,
等弧的弧长相等.
练习
A
3.在半径为4的大⊙O中,EF所对的圆心角是600 ,则弧长= s =
1200
C
D
O
E
F
600
B
A
O
4.如图,在半径为4的⊙O中,AB长为 ,
则扇形的面积是 是
练习
600
想一想:扇形的面积公式
与什么公式类似?
探究点三 扇形的面积与弧长的关系公式
R
l
h
a
问题解决
空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,这头牛吃草的最大活动区域有多大?
O
B
A
1200
变式
如图,草地上有一根柱子,柱子两旁有两排栅栏,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,这头牛吃草的最大活动区域有多大?
A
D
B
C
O
解析:如图,大扇形的圆心角是90度,半径是5m,
所以面积是 ,小扇形
的圆心角是180°-120°=60°,半径是
1m,则面积= , ∴小牛A
在草地上的最大活动区域面积=
大扇形的圆心角是90度,大扇大扇形的圆心角是90度,形的圆心角是90度,
1200
O
B
900
C
A
1、已知扇形的圆心角是120°,半径为6,则扇形的弧长是( );
2、如图1所示,把边长为2的正方形ABCD的一边放在定直线l上,按顺时针方向绕D旋转
到如图的位置,则点B运
动到点B′所经过
的路线长度为( );
3、 如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为( )
当堂检测
2
A
D
B
B
L
C’
C
(A’)
A
D
B
B’
L
C’
4、如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是( )
当堂检测
小结
本节课你有什么收获?
公式:
思想: 类比+转化
“知之者不如好之者,好之者不如乐之者。” 兴趣是走向成功的原动力,保持浓厚的学习兴趣,你会享受到更多成功的乐趣。
老师寄语
作业
必做题 教科书 P115 1,2,3.
选做题 《基训》P112 11,12
谢 谢 !
同课章节目录
