24.1.2 垂直于弦的直径 课件(共19张PPT) 2023--2024学年人教版九年级数学上册
文档属性
| 名称 | 24.1.2 垂直于弦的直径 课件(共19张PPT) 2023--2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 21:58:00 | ||
图片预览


文档简介
(共19张PPT)
用
应
径
的
定
论
理
罗亭学校
徐娒
18
22
1、掌握垂径定理及其推论,并用它解决有关证明及计算问题。
学习目标
2、进一步体会和理解从特殊到一般和从一般到特殊的思想方法。
3、欣赏几何图形的对称美和变化美,进一步体会数学的美丽和价值。
=i=
22
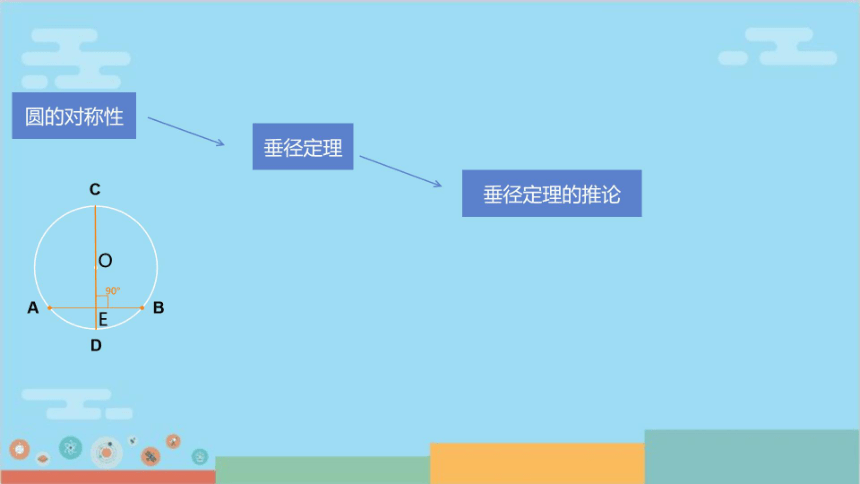
圆的对称性
垂径定理
垂径定理的推论
90°
B
D
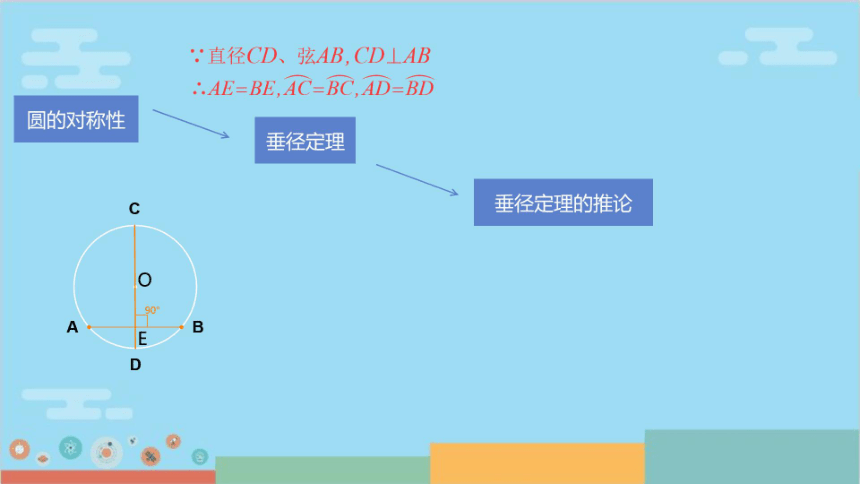
,直径CD、弦AB,CD⊥AB
2
..AE=BE,AC=BC.AD=BD
圆的对称性
垂径定理
C
垂径定理的推论
90°
B
D
,'直径CD、弦AB,CD⊥AB
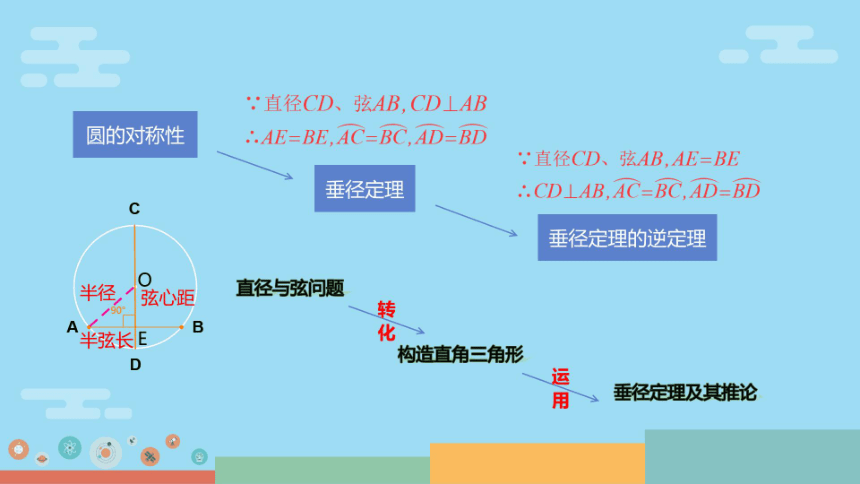
圆的对称性
..AE=BE,AC=BC.AD=BD
.'直径CD、弦AB,AE=BE
垂径定理
.CD⊥AB,AC=BC,AD=BD
垂径定理的逆定理
半径
弦心距
直径与弦问题
90
转
A
B
半弦长E
化
D
构造直角三角形
运
用
垂径定理及其推论
一弦一直径垂直
90°
90
%
909
A
B
A
B
B
B
特殊
D
D
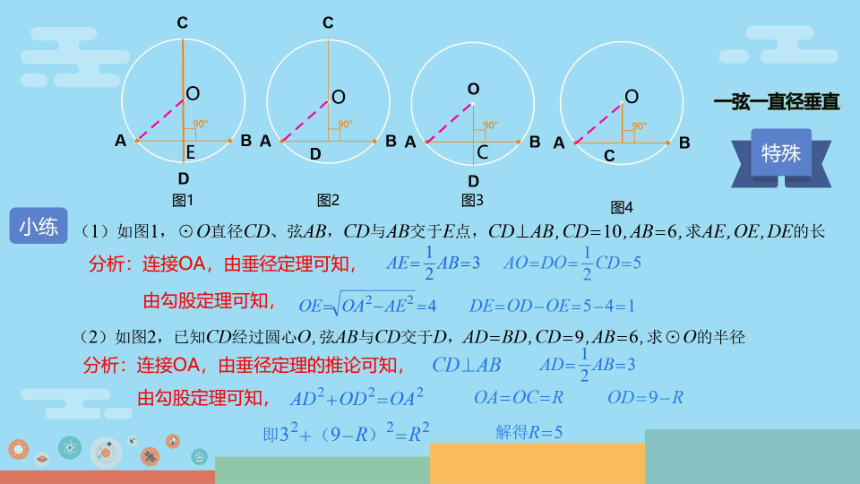
图1
图2
图3
图4
小练
(1)如图1,⊙O直径CD、弦AB,CD与AB交于E点,CD⊥AB,CD=10,AB=6,求AE,OE,DE的长
分析:连接OA,由垂径定理可知,
AE=AB=3 A0=DO=ICD=5
由勾股定理可知,
OEOA2-AE2=4
DE-OD-OE-5-4-1
(2)如图2,已知CD经过圆心O,弦AB与CD交于D,AD=BD,CD=9,AB=6,求⊙O的半径
分析:连接OA,由垂径定理的推论可知,CD LAB
AD=24B=3
由勾股定理可知,AD2+OD2=OA2
OA-OC=R
OD=9-R
即32+(9-R)2=R2
解得R=5
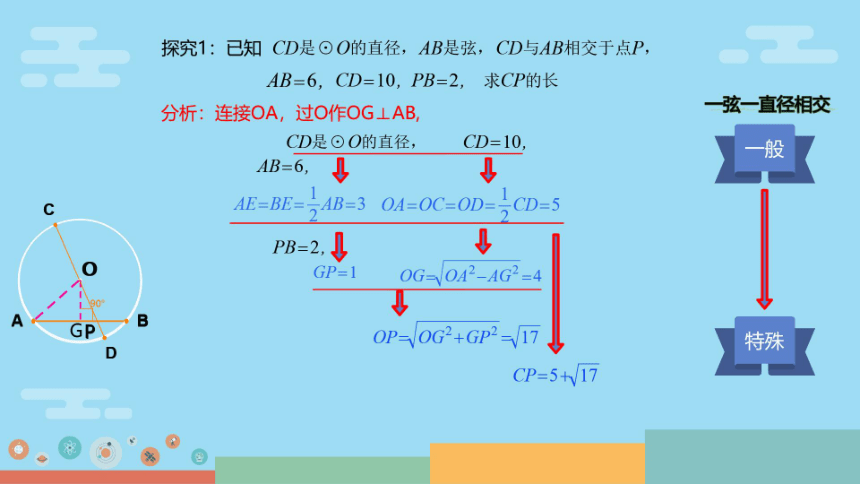
探究1:已知CD是⊙O的直径,AB是弦,CD与AB相交于点P,
AB=6,CD=10,PB=2,求CP的长
分析:连接OA,过O作DGLAB,
一弦一直径相交
CD是⊙O的直径,
CD=10,
般
AB=6,↓
↓
C
AE=BE=AB=3 0A=OC=OD=CD=5
PB=2,↓
↓
GP=1
OG-042-4G2-4
B
0P-/0G2+GP2-√17
特殊
CP=5+17
变式:已知
CB是⊙O的直径,AB是弦,半径OF⊥AB于点E,
AB=6,EF=1,求弦CA的长
分析:
CB是⊙O的直径,
AB是弦,半径OF⊥AB于点E,
一弦一直径相交
↓
↓
AB=6↓
般
C
点O是CB的中点
点E是AB的中点
EB=AB=3
2
90
OE是△ABC的中位线
OE2+EB2=OB2
B(D)
↓
即0E2+32=(0E+1)2
CA-20E
解得OE=4
↓
特殊
CA=8
用
应
径
的
定
论
理
罗亭学校
徐娒
18
22
1、掌握垂径定理及其推论,并用它解决有关证明及计算问题。
学习目标
2、进一步体会和理解从特殊到一般和从一般到特殊的思想方法。
3、欣赏几何图形的对称美和变化美,进一步体会数学的美丽和价值。
=i=
22
圆的对称性
垂径定理
垂径定理的推论
90°
B
D
,直径CD、弦AB,CD⊥AB
2
..AE=BE,AC=BC.AD=BD
圆的对称性
垂径定理
C
垂径定理的推论
90°
B
D
,'直径CD、弦AB,CD⊥AB
圆的对称性
..AE=BE,AC=BC.AD=BD
.'直径CD、弦AB,AE=BE
垂径定理
.CD⊥AB,AC=BC,AD=BD
垂径定理的逆定理
半径
弦心距
直径与弦问题
90
转
A
B
半弦长E
化
D
构造直角三角形
运
用
垂径定理及其推论
一弦一直径垂直
90°
90
%
909
A
B
A
B
B
B
特殊
D
D
图1
图2
图3
图4
小练
(1)如图1,⊙O直径CD、弦AB,CD与AB交于E点,CD⊥AB,CD=10,AB=6,求AE,OE,DE的长
分析:连接OA,由垂径定理可知,
AE=AB=3 A0=DO=ICD=5
由勾股定理可知,
OEOA2-AE2=4
DE-OD-OE-5-4-1
(2)如图2,已知CD经过圆心O,弦AB与CD交于D,AD=BD,CD=9,AB=6,求⊙O的半径
分析:连接OA,由垂径定理的推论可知,CD LAB
AD=24B=3
由勾股定理可知,AD2+OD2=OA2
OA-OC=R
OD=9-R
即32+(9-R)2=R2
解得R=5
探究1:已知CD是⊙O的直径,AB是弦,CD与AB相交于点P,
AB=6,CD=10,PB=2,求CP的长
分析:连接OA,过O作DGLAB,
一弦一直径相交
CD是⊙O的直径,
CD=10,
般
AB=6,↓
↓
C
AE=BE=AB=3 0A=OC=OD=CD=5
PB=2,↓
↓
GP=1
OG-042-4G2-4
B
0P-/0G2+GP2-√17
特殊
CP=5+17
变式:已知
CB是⊙O的直径,AB是弦,半径OF⊥AB于点E,
AB=6,EF=1,求弦CA的长
分析:
CB是⊙O的直径,
AB是弦,半径OF⊥AB于点E,
一弦一直径相交
↓
↓
AB=6↓
般
C
点O是CB的中点
点E是AB的中点
EB=AB=3
2
90
OE是△ABC的中位线
OE2+EB2=OB2
B(D)
↓
即0E2+32=(0E+1)2
CA-20E
解得OE=4
↓
特殊
CA=8
同课章节目录
