4.3 角 课件(共29张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 4.3 角 课件(共29张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 22:10:20 | ||
图片预览








文档简介
(共29张PPT)
新课标 北师大版
七年级上册
4.3角
第四章
基本平面图形
学习目标
1.通过对现实情境中实物的观察分析,能用自己的语言表达角的概念,进一步认识锐角、钝角、平角、周角及其大小关系;
2.会用常见的几种方法表示角;
3.认识角的常用度量单位:度分秒,并会进行简单的换算.
新课引入
你能不能从图中找到角?
核心知识点一
探究学习
角的概念和分类
1、角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
O
2、角也可以看成由一条射线绕着它的端点旋转而成的.
它的端点就是角的顶点.
开始时的射线称为始边,
旋转结束后的射线称为终边.
始边
终边
O
A
B
(B)
平角
周角
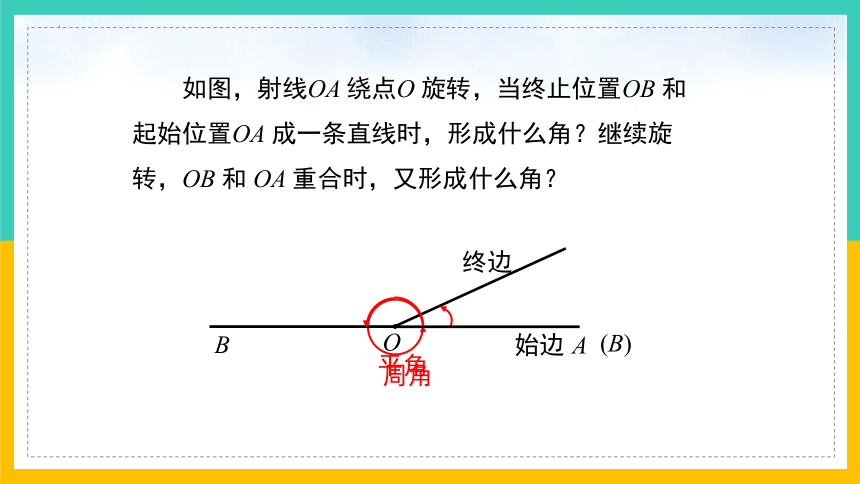
如图,射线OA 绕点O 旋转,当终止位置OB 和起始位置OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
练一练:1.判断正误.
(1)有公共端点的两条射线叫做角.( )
(2)两条射线组成的图形叫做角.( )
(3)角的大小与角画出的两边的长短无关.( )
(4)由一条射线绕一点旋转而形成的图形叫做角.( )
×
×
×
√
2.下列说法正确的是( )
A. 平角是一条直线
B. 一条射线是一个周角
C. 两条射线组成的图形叫做角
D. 两边成一直线的角是平角
D
核心知识点二
角的表示
A
B
O
表示法:∠AOB 或∠BOA
O是角的顶点,A、B分别是角两边上的一点,A、B可以交换位置,但O必须写在中间. 任何角都可以用此方法表示.
角的符号:
1、用角的符号及三个大写字母表示:
O
表示法:∠O
当以某一个字母(如O)为顶点的角只有一个角时可以这样表示. 若以O为顶点的角有若干个时,不能用此表示法.
A
B
A
B
C
O
这种情形不能表示为∠O
2、用角的符号及一个大写字母表示
表示法:∠1
用此法时, 必须在近顶点处加上弧线并注上阿拉伯数字或小写希腊字母α、β、γ .
1
α
表示法:∠α
1
2
3、用角的符号及一个数字或希腊字母来表示:
方法 图标 记法 适用范围
用三个大写字母
用一个大写字母
用一个希腊字母
用一个数字 任何角
顶点处只有一角
只能表示单独一个角
O
A
B
O
A
B
∠AOB或∠BOA
∠O
∠ α
α
1
∠ 1
角的表示方法总结
∠BAD,∠BAE,∠BAC,∠DAE,∠DAC,∠EAC
∠B,∠C
练一练:根据下图填空:
(1)图中能用顶点的一个
大写字母表示的角有__________;
(2)以A为顶点的角有
_______________________________________________.
核心知识点三
角的单位与计算
角的度量工具:
量角器.
怎么知道这个角的大小?
量角器的使用方法:
点对点、线对线、从零开始看:
1、角的顶点和量角器中心点对齐。
2、角的任意一条边和量角器的0刻度线对齐。
3、对齐角的边应该指量角器的0度(分清楚指的外圈还是内圈)从0开始查度数。
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是1度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角60等分,每一份叫做1秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
(1)1.45°等于多少分 等于多少秒
(2)1800″等于多少分 等于多少度
解: (1)60′×1.45
=87′,
即 1.45°=87′=5220″;
(2) × 1800=
30′,
60″×87
=5220″,
× 30 =
0.5°,
即 1800″=30′=0.5°.
例:计算:
例.计算:
(1)49°38′+66°22′;
(2)180°-79°19′;
(3)22°16′×5;
(4)182°36′÷4.
解:原式=(49°+66°)+(38′+22′)=115°+1°=116°.
原式=(179°-79°)+(60′-19′)=100°+41′=100°41′.
原式=22°×5+16′×5=110°+80′=111°+20′=111°20′.
原式=182°÷4+36′÷4=45°30′+9′=45°39′.
随堂练习
1.如图,从∠AOB的顶点引出两条射线OC,OD,图中的角共有( )
A.3个
B.4个
C.6个
D.7个
C
2.如图,下列表示角的方法中,不正确的是 ( )
A.∠A
B.∠E
C.∠a
D.∠1
B
3.如图,钟表上10点整时,时针与分针所成的角是( )
A.30°
B.60°
C.90°
D.120°
B
4.如图,下列说法:
(1)∠ECG 和∠C是同一个角;
(2)∠OGF 和∠DGB是同一个角;
(3)∠DOF 和∠EOG是同一个角;
(4)∠ABC 和∠ACB不是同一个角.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
C
5. 0.25°等于多少分 等于多少秒
解: 60′× 0.25 = 15′,60″× 15 = 900″.
即0.25°= 15′= 900″.
6. 2700″等于多少分 等于多少度
解:
( ) ′ ×2700=45′, ( ) °×45=0.75°.
即2700″=45′=0.75°.
7.如图,以B为顶点的角有哪几个?以C为顶点的角有哪几个?以D为顶点的角有哪几个?用恰当方法把它们分别表示出来.
解:以B为顶点的角有:∠ABC,∠ABD,∠DBC;
以C为顶点的角有:∠C;以D为顶点的角有:
∠1,∠ADE,∠BDC,∠β
8.计算:
(1)28°32′46″+ 15°36′48″
(2)(30°-23°15′40″)×3
(3)108°18′36″-56.5°(结果用度、分、秒表示)
(4)123°24′-60 °36′ (结果用度表示)
解:(1) 28°32′46″+ 15°36′48″
= (28°+15°)+(32′+36′)+(46″+48″)
= 43°68′94″
= 44°9′34″.
(2) (30°-23°15′40″)×3
=6°44′20″×3
=18°132′60″
=20°13′
(3) 108°18′36″-56.5°
=108°18′36″-56°30′
=107°78′36″-56°30′
=51°48′36″
(4) 123°24′-60 °36′
=122°84′- 60°36′
=62°48′
=62.8°
课堂小结
角
角的概念
角的度量与计算
角的表示方法
定义1:有公共端点的两条射线组成的图形
定义2:一条射线绕着它的端点旋转而成的图形
1、用三个大写字母或一个大写字表示
2、用一个数字表示
3、用一个希腊字母表示
1°=60′;1分=60″
谢谢聆听
新课标 北师大版
七年级上册
4.3角
第四章
基本平面图形
学习目标
1.通过对现实情境中实物的观察分析,能用自己的语言表达角的概念,进一步认识锐角、钝角、平角、周角及其大小关系;
2.会用常见的几种方法表示角;
3.认识角的常用度量单位:度分秒,并会进行简单的换算.
新课引入
你能不能从图中找到角?
核心知识点一
探究学习
角的概念和分类
1、角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
O
2、角也可以看成由一条射线绕着它的端点旋转而成的.
它的端点就是角的顶点.
开始时的射线称为始边,
旋转结束后的射线称为终边.
始边
终边
O
A
B
(B)
平角
周角
如图,射线OA 绕点O 旋转,当终止位置OB 和起始位置OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
练一练:1.判断正误.
(1)有公共端点的两条射线叫做角.( )
(2)两条射线组成的图形叫做角.( )
(3)角的大小与角画出的两边的长短无关.( )
(4)由一条射线绕一点旋转而形成的图形叫做角.( )
×
×
×
√
2.下列说法正确的是( )
A. 平角是一条直线
B. 一条射线是一个周角
C. 两条射线组成的图形叫做角
D. 两边成一直线的角是平角
D
核心知识点二
角的表示
A
B
O
表示法:∠AOB 或∠BOA
O是角的顶点,A、B分别是角两边上的一点,A、B可以交换位置,但O必须写在中间. 任何角都可以用此方法表示.
角的符号:
1、用角的符号及三个大写字母表示:
O
表示法:∠O
当以某一个字母(如O)为顶点的角只有一个角时可以这样表示. 若以O为顶点的角有若干个时,不能用此表示法.
A
B
A
B
C
O
这种情形不能表示为∠O
2、用角的符号及一个大写字母表示
表示法:∠1
用此法时, 必须在近顶点处加上弧线并注上阿拉伯数字或小写希腊字母α、β、γ .
1
α
表示法:∠α
1
2
3、用角的符号及一个数字或希腊字母来表示:
方法 图标 记法 适用范围
用三个大写字母
用一个大写字母
用一个希腊字母
用一个数字 任何角
顶点处只有一角
只能表示单独一个角
O
A
B
O
A
B
∠AOB或∠BOA
∠O
∠ α
α
1
∠ 1
角的表示方法总结
∠BAD,∠BAE,∠BAC,∠DAE,∠DAC,∠EAC
∠B,∠C
练一练:根据下图填空:
(1)图中能用顶点的一个
大写字母表示的角有__________;
(2)以A为顶点的角有
_______________________________________________.
核心知识点三
角的单位与计算
角的度量工具:
量角器.
怎么知道这个角的大小?
量角器的使用方法:
点对点、线对线、从零开始看:
1、角的顶点和量角器中心点对齐。
2、角的任意一条边和量角器的0刻度线对齐。
3、对齐角的边应该指量角器的0度(分清楚指的外圈还是内圈)从0开始查度数。
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是1度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角60等分,每一份叫做1秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
(1)1.45°等于多少分 等于多少秒
(2)1800″等于多少分 等于多少度
解: (1)60′×1.45
=87′,
即 1.45°=87′=5220″;
(2) × 1800=
30′,
60″×87
=5220″,
× 30 =
0.5°,
即 1800″=30′=0.5°.
例:计算:
例.计算:
(1)49°38′+66°22′;
(2)180°-79°19′;
(3)22°16′×5;
(4)182°36′÷4.
解:原式=(49°+66°)+(38′+22′)=115°+1°=116°.
原式=(179°-79°)+(60′-19′)=100°+41′=100°41′.
原式=22°×5+16′×5=110°+80′=111°+20′=111°20′.
原式=182°÷4+36′÷4=45°30′+9′=45°39′.
随堂练习
1.如图,从∠AOB的顶点引出两条射线OC,OD,图中的角共有( )
A.3个
B.4个
C.6个
D.7个
C
2.如图,下列表示角的方法中,不正确的是 ( )
A.∠A
B.∠E
C.∠a
D.∠1
B
3.如图,钟表上10点整时,时针与分针所成的角是( )
A.30°
B.60°
C.90°
D.120°
B
4.如图,下列说法:
(1)∠ECG 和∠C是同一个角;
(2)∠OGF 和∠DGB是同一个角;
(3)∠DOF 和∠EOG是同一个角;
(4)∠ABC 和∠ACB不是同一个角.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
C
5. 0.25°等于多少分 等于多少秒
解: 60′× 0.25 = 15′,60″× 15 = 900″.
即0.25°= 15′= 900″.
6. 2700″等于多少分 等于多少度
解:
( ) ′ ×2700=45′, ( ) °×45=0.75°.
即2700″=45′=0.75°.
7.如图,以B为顶点的角有哪几个?以C为顶点的角有哪几个?以D为顶点的角有哪几个?用恰当方法把它们分别表示出来.
解:以B为顶点的角有:∠ABC,∠ABD,∠DBC;
以C为顶点的角有:∠C;以D为顶点的角有:
∠1,∠ADE,∠BDC,∠β
8.计算:
(1)28°32′46″+ 15°36′48″
(2)(30°-23°15′40″)×3
(3)108°18′36″-56.5°(结果用度、分、秒表示)
(4)123°24′-60 °36′ (结果用度表示)
解:(1) 28°32′46″+ 15°36′48″
= (28°+15°)+(32′+36′)+(46″+48″)
= 43°68′94″
= 44°9′34″.
(2) (30°-23°15′40″)×3
=6°44′20″×3
=18°132′60″
=20°13′
(3) 108°18′36″-56.5°
=108°18′36″-56°30′
=107°78′36″-56°30′
=51°48′36″
(4) 123°24′-60 °36′
=122°84′- 60°36′
=62°48′
=62.8°
课堂小结
角
角的概念
角的度量与计算
角的表示方法
定义1:有公共端点的两条射线组成的图形
定义2:一条射线绕着它的端点旋转而成的图形
1、用三个大写字母或一个大写字表示
2、用一个数字表示
3、用一个希腊字母表示
1°=60′;1分=60″
谢谢聆听
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
