4.2 比较线段的长短 课件(共25张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 4.2 比较线段的长短 课件(共25张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
新课标 北师大版
七年级上册
4.2比较线段的长短
第四章
基本平面图形
学习目标
了解“两点之间线段最短”的性质以及两点间距
离的概念.
2. 理解线段中点的概念及表示方法.
3. 能借助直尺、圆规等工具比较两条线段的长短
新课引入
从教室到图书馆,总有少数同学横穿草坪,你能用数学知识来解释吗?
核心知识点一
探究学习
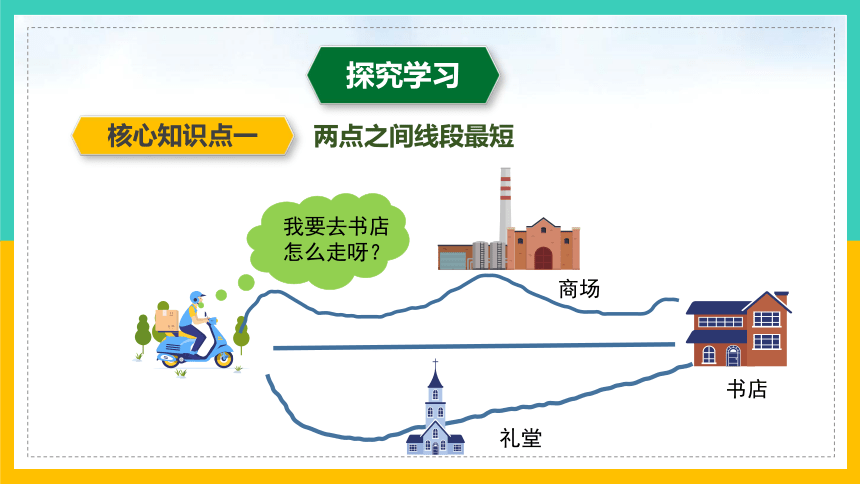
两点之间线段最短
我要去书店怎么走呀?
商场
书店
礼堂
两点之间的所有连线中,线段最短
根据生活经验,容易发现:
这一事实可以简述为:两点之间线段最短.
我们把两点之间线段的长度,叫做这两点之间的距离.
现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
A.过一点有无数条直线
B.两点之间线段的长度,叫做这两点之间的距离
C.两点确定一条直线
D.两点之间,线段最短
D
[解析] 在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.
例:如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P
核心知识点二
比较两条线段的长短
生活中我们常常会比较两个物体的长短。如图两支铅笔谁长
我们可以把两支铅笔看成两条线段,这样我们就把实际问题转化为了几何问题.
思考:怎样比较两条线段的长短 ?
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
A B
C D
a
b
(1)度量法
用刻度尺量出它们的长度,再进行比较.
C
D
(A)
B
<
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
借助尺规作图的方法
如图,已知线段AB,用尺规作一条线段等于已知线段AB.
(1)作射线A'C';
∴线段A'B'即为所求.
A' C'
B'
A
B
解:作图步骤如下:
(2)以点A′为圆心,以线段AB的长度为半径画弧,交射线A′C′于点B'.使A'B'=AB.
做一做
如图,已知线段 a,b,求作线段 AB=2a+b.
解析: 作线段 AB=2a+b,实际就是顺次作三条线段分别等于 a,a 和 b.
解:作图步骤如下:
(1)作射线 AM;
(2)在 AM 上顺次截取 AB1=a,B1B2=a,B2B=b,则线段 AB=2a+b.
A
M
a
a
b
B1
B2
B
核心知识点三
线段的中点
利用尺规作图,我们可以作一条线段等于另一条线段的两倍,如图:AB=2AM.
A
B
M
根据作图可知:AM=MB,此时点M把线段AB分成了两条相等的线段.
把一条线段分成相等线段的点,叫做线段的中点.
A
B
M
如图,点M就是线段AB的中点.
思考:如图,若线段AB的中点是点M,你能得到哪些线段间的数量关系?
符号语言
A
B
M
例:如图,在直线上有A,B,C三点,AB= 4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:∵AB=4 cm,BC=3 cm,
∴ AC=AB+ BC=3+4=7 cm.
∵点O是线段AC的中点,
∴ OC= AC= 7 × =3.5 cm.
∴ OB=OC-BC=3.5-3=0.5(cm).
(1) 逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.
计算线段长度的一般方法:
归纳总结
(2) 整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
随堂练习
1.下列说法正确的是( )
A.连接两点的线段叫做两点间的距离
B.两点间的连线的长度叫做两点间的距离
C.连接两点的直线的长度叫做两点间的距离
D.连接两点的线段的长度叫做两点间的距离
D
2. 点B在直线AC上,线段AB=5,BC=3,则A,C两点间的距离是( )
A.8 B.2
C.8或2 D.无法确定
C
3.如图所示,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.无法确定
C
4.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的 是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
C
5.如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店B,请你帮助他选择一条最近的路线( )
A.A→C→D→B B.A→C→F→B
C.A→C→E→F→B D.A→C→M→B
B
6.如图,C,D,E是线段AB上的三个点,下面关于线段CE的表示:
①CE=CD+DE; ②CE=BC﹣EB;
③CE=CD+BD﹣AC; ④CE=AE+BC﹣AB.
其中正确的是 (填序号).
①②④
7.如图,B,C两点把线段AD分成2∶4∶3三部分,M是AD的中点,CD=6,求线段MC的长.
解:AB=6÷3×2=4,BC=6÷3×4=8,AD=AB+BC+CD=18,因为M是AD的中点,所以MD= AD=9,MC=MD-CD=3
8.如图点A,B,E,C,D在同一直线上,且AC=BD,E是BC的中点,试说明E也是AD的中点.
解:因为AC=BD,所以AC-BC=BD-BC,所以AB=CD,因为E是BC的中点,所以BE=EC,所以BE+AB=EC+CD,即AE=ED,所以E也是AD的中点.
课堂小结
比较线段的长短
两点之间线段最短
比较线段大小的方法
线段的中点
度量法
叠合法
谢谢聆听
新课标 北师大版
七年级上册
4.2比较线段的长短
第四章
基本平面图形
学习目标
了解“两点之间线段最短”的性质以及两点间距
离的概念.
2. 理解线段中点的概念及表示方法.
3. 能借助直尺、圆规等工具比较两条线段的长短
新课引入
从教室到图书馆,总有少数同学横穿草坪,你能用数学知识来解释吗?
核心知识点一
探究学习
两点之间线段最短
我要去书店怎么走呀?
商场
书店
礼堂
两点之间的所有连线中,线段最短
根据生活经验,容易发现:
这一事实可以简述为:两点之间线段最短.
我们把两点之间线段的长度,叫做这两点之间的距离.
现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
A.过一点有无数条直线
B.两点之间线段的长度,叫做这两点之间的距离
C.两点确定一条直线
D.两点之间,线段最短
D
[解析] 在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.
例:如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P
核心知识点二
比较两条线段的长短
生活中我们常常会比较两个物体的长短。如图两支铅笔谁长
我们可以把两支铅笔看成两条线段,这样我们就把实际问题转化为了几何问题.
思考:怎样比较两条线段的长短 ?
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
A B
C D
a
b
(1)度量法
用刻度尺量出它们的长度,再进行比较.
C
D
(A)
B
<
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
借助尺规作图的方法
如图,已知线段AB,用尺规作一条线段等于已知线段AB.
(1)作射线A'C';
∴线段A'B'即为所求.
A' C'
B'
A
B
解:作图步骤如下:
(2)以点A′为圆心,以线段AB的长度为半径画弧,交射线A′C′于点B'.使A'B'=AB.
做一做
如图,已知线段 a,b,求作线段 AB=2a+b.
解析: 作线段 AB=2a+b,实际就是顺次作三条线段分别等于 a,a 和 b.
解:作图步骤如下:
(1)作射线 AM;
(2)在 AM 上顺次截取 AB1=a,B1B2=a,B2B=b,则线段 AB=2a+b.
A
M
a
a
b
B1
B2
B
核心知识点三
线段的中点
利用尺规作图,我们可以作一条线段等于另一条线段的两倍,如图:AB=2AM.
A
B
M
根据作图可知:AM=MB,此时点M把线段AB分成了两条相等的线段.
把一条线段分成相等线段的点,叫做线段的中点.
A
B
M
如图,点M就是线段AB的中点.
思考:如图,若线段AB的中点是点M,你能得到哪些线段间的数量关系?
符号语言
A
B
M
例:如图,在直线上有A,B,C三点,AB= 4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:∵AB=4 cm,BC=3 cm,
∴ AC=AB+ BC=3+4=7 cm.
∵点O是线段AC的中点,
∴ OC= AC= 7 × =3.5 cm.
∴ OB=OC-BC=3.5-3=0.5(cm).
(1) 逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.
计算线段长度的一般方法:
归纳总结
(2) 整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
随堂练习
1.下列说法正确的是( )
A.连接两点的线段叫做两点间的距离
B.两点间的连线的长度叫做两点间的距离
C.连接两点的直线的长度叫做两点间的距离
D.连接两点的线段的长度叫做两点间的距离
D
2. 点B在直线AC上,线段AB=5,BC=3,则A,C两点间的距离是( )
A.8 B.2
C.8或2 D.无法确定
C
3.如图所示,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.无法确定
C
4.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的 是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
C
5.如图所示,某同学的家在A处,星期日他到书店去买书,想尽快赶到书店B,请你帮助他选择一条最近的路线( )
A.A→C→D→B B.A→C→F→B
C.A→C→E→F→B D.A→C→M→B
B
6.如图,C,D,E是线段AB上的三个点,下面关于线段CE的表示:
①CE=CD+DE; ②CE=BC﹣EB;
③CE=CD+BD﹣AC; ④CE=AE+BC﹣AB.
其中正确的是 (填序号).
①②④
7.如图,B,C两点把线段AD分成2∶4∶3三部分,M是AD的中点,CD=6,求线段MC的长.
解:AB=6÷3×2=4,BC=6÷3×4=8,AD=AB+BC+CD=18,因为M是AD的中点,所以MD= AD=9,MC=MD-CD=3
8.如图点A,B,E,C,D在同一直线上,且AC=BD,E是BC的中点,试说明E也是AD的中点.
解:因为AC=BD,所以AC-BC=BD-BC,所以AB=CD,因为E是BC的中点,所以BE=EC,所以BE+AB=EC+CD,即AE=ED,所以E也是AD的中点.
课堂小结
比较线段的长短
两点之间线段最短
比较线段大小的方法
线段的中点
度量法
叠合法
谢谢聆听
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
