3.4实际问题与一元一次方程(第1课时 )课件(共28张PPT)
文档属性
| 名称 | 3.4实际问题与一元一次方程(第1课时 )课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 12:36:21 | ||
图片预览








文档简介
(共28张PPT)
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第三章一元一次方程
3.4实际问题与一元一次方程
(第一课时)产品配套问题和工程问题
1.理解配套问题和工程问题的背景.
2.掌握用一元一次方程解决实际问题的基本过程.
3.分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
学习目标
复习提问
一元一次方程的求解步骤是什么?
实例引入
生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
典例解析
例1.某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母. 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
产品类型 生产人数 单人产量 总产量
螺钉 1200
螺母 2000
列表分析:
x
22-x
1200 x
2000(22-x)
螺母总量=螺钉总量×2
提示:这类问题中配套的物品之间具有一定的数量关系,这可以作为列方程的依据.
分析:每天生产的螺母数量是螺钉数量的2倍时,它们刚好配套.
典例解析
解:设应安排x名工人生产螺母,(22-x)名工人生产螺钉.根据螺母数量应是螺钉数量的2倍,列出方程
2×1200(22-x)=2000x
解方程,得 x=12
所以 22-x=10
答:应安排10名工人生产螺钉,12名工人生产螺母.
解法1
典例解析
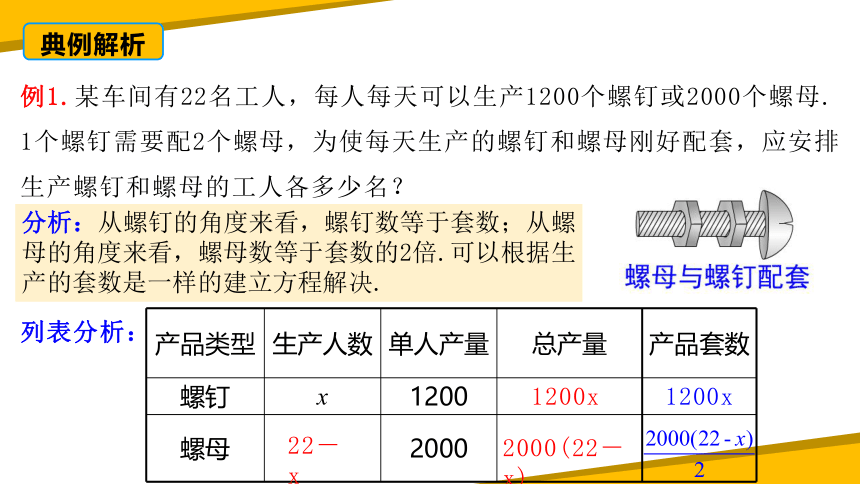
例1.某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母. 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析:从螺钉的角度来看,螺钉数等于套数;从螺母的角度来看,螺母数等于套数的2倍.可以根据生产的套数是一样的建立方程解决.
列表分析:
产品类型 生产人数 单人产量 总产量 产品套数
螺钉 x 1200
螺母 2000
1200x
22-x
2000(22-x)
1200x
典例解析
解法2
解:设应安排 x 名工人生产螺钉,(22-x)名工人生产螺母.依题意,得
解方程,得 x=10.
所以 2-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
建立模型
方法归纳
解决配套问题的思路:
1.利用配套问题中物品之间具有的数量关系作为列方程的依据;
2.利用配套问题中的套数不变作为列方程的依据.
典例解析
例2.某服装厂要生产一批校服,已知每3m的布料可以做2件上衣或3条裤子,要求一件上衣和两条裤子配一套,现有1008m的布料,应怎样计划用料才能做尽可能多的成套校服 校服有多少套
典例解析
例3.整理一批图书,由一个人做要40h完成.现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
解:设安排x人先做4h. 根据先后两个时段的工作量之和应等于总工作量,列出方程
解得x=2
答:应安排2人先做4h.
随堂练习
1.某防护服厂有54人,每人每天可加工防护服8件或防护面罩10个,已知一件防护服配一个防护面罩,为了使每天生产的防护服与防护面罩正好配套,需要安排多少人生产防护服?
解:设需要安排x人生产防护服,则安排(54-x)人生产防护面罩.
由题意,得8x=10(54-x),
解得x=30.
答:需要安排30人生产防护服.
随堂练习
2.一张方桌由1个桌面、4条桌腿组成,如果1m3木料可以做50个桌面或300条桌腿,现有5m3木料,要使做出的桌面和桌腿恰好配成方桌,应用多少木料来做桌面 能配成多少张方桌
解:设应用xm3木料做桌面,则用(5-x)m3木料做桌腿.
根据题意得50x×4=300(5-x),
解得x=3.
则能配成方桌50×3=150(张).
答:应用3m3木料做桌面,能配成150张方桌.
随堂练习
3.将一段长为1.2km的河道的整治任务交由甲、乙两个工程队接力完成,共用时60天.已知甲队每天整治24m,乙队每天整治16m,则甲队整治河道_______m,乙队整治河道_______m.
4.有一段长为146m的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26m.已知甲工程队每天比乙工程队多掘进2m,按此速度施工,甲、乙两个工程队还需联合工作______天.
720
480
10
随堂练习
5.一项工程,甲单独做10天可以完成,乙单独做15天可以完成,现甲队先做2天,余下的工程由两队共同做x天刚好可以完成,则由题意可列出的方程是___________________.
中考链接
(2017·滨州)某车间有27名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺母16个或螺栓22个,若分配x名工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下面所列方程中正确的是( )
A.22x=16(27-x) B.16x=22(27-x)
C.2×16x=22(27-x) D.2×22x=16(27-x)
D
课堂小结
列方程解决实际问题的一般步骤:
审:审清题意,分清题中的已知量、未知量.
设:设未知数,设其中某个未知量为x.
列:根据题意寻找等量关系列方程.
解:解方程.
验:检验方程的解是否符合题意.
答:写出答案 (包括单位).
当堂测试
1. 某机械厂加工车间有33名工人,平均每名工人每天加工大齿轮5个或小齿轮15个,已知2个大齿轮和3个小齿轮配成一套,问分别安排多少名工人加工大,小齿轮,才能刚好配套?若设加工大齿轮的工人有名,则可列方程是( )
A.2×5(33-x)=3×15x B.2×5x=3×15(33-x)
C.3×5x=2×15(33-x) D.3×5(33-x)=2×15x
2. 2020年,新冠疫情肆虐全球,口罩成了人们出行的“标配”,某口置生产车间有26名工人,每人每天可以生产800个口置面或1000根口置带,1个口置面需要配2根口置带,为了使每天生产口置面和口置带刚好配套,设安排x名工人生产口置面,则下面所列方程正确的是( )
A.1000(26-x)=2×800x B.1000(13-x)=800x
C.2×1000(26-x)=800x D.1000(26-x)=800x
C
A
当堂测试
3. 我国明代数学读本《算法统宗》中有一道题,其题意为;客入一起分银子,若每人6两还剩3两;若每人8两,还差4两,问银子共有几两?没银子共有x两,则可列方程为( )
A,6x+3=8x-4 B.6x-3=8x+4
C. D.
C
当堂测试
4. 众所周知,中华诗词博大精深,集大量的情景情感于短短数十字之间,或豪放,或婉约,或思民生疾苦,或抒发己身豪情逸致,文化价值极高。而数学与古诗词更是有着密切的联系.古诗中,五言绝句是四句诗,每句都是五个字;七言绝句是四句诗,每句都是七个字。有一本诗集,其中五言绝句比七言绝句多13首,总字数却反而少了20个字.问两种诗各多少首?设七言绝句有x首,根据题意,可列方程为 .
5. 元代《算学启蒙》里有这样一道题:“良马日行二百四十里,弩马日行一百五十里,弩马先行十二日,问良马几何追及之?”设良马x天能追上弩马,可列方程为 .
28x-20(x+13)=20
150×12+150x=240x
当堂测试
6. 全班有54人去公园划船,一共租用了10只船.每只大船坐6人,每只小船坐4人,且所有的船刚好坐满.租用的大船,小船各有多少只?
解:设租用的大船x只,则租用的小船(10-x)只,由题意得
6x+4(10-x)=54,
解得:x=7,
10-x=10-7=3(只)
答:租用的大船,小船各有7只和3只
分层作业
【基础达标作业】
1. 为鼓励居民节约用水,某市对居民用水实行“阶梯收费”,规定每户每月用水量不超过10吨,水价为每吨2元;超过10吨的部分每吨3.5元.已知小莉家某月交水费34元,则小莉家该月用水多少吨?若设小莉家该月用水x吨,则可列方程为( )
A.2×10-3.5×(x-10)=34 B.3.5×10+2×(x-10)=34
C.2×10+3.5×(10-x)-34 D.2×10+3.5×(x-10)=34
D
分层作业
2. 随着国力的提升,琳琅满目的消费品开始不断刷新着各阶层人民的满足感,每逢年末,促销手段层出不迭,某超市中,一种商品每件的标价是330元,按标价的八折销售时,可获利10%,设这种商品每件的进价为x元,可列方程为( )
330× =10%x B. 330 x=10%x
C. 330× =(1+10%)x D. x=
B
分层作业
3.我国古代《孙子算经》卷中记载“多人共车”问题,其原文如下:今有三人共车,二车空,二人共车,九人步,问人与车各几何?其大意为:若3个人乘一辆车,则空2辆车;若2个人乘一辆车,则有9个人要步行,问人与车数各是多少?若设有2个人,则可列方程是( )
A.3(x+2)=2x-9 B.3(x+2)=2x-9
C. D.
C
分层作业
【能力提升作业】
4. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,”诗中后面两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.设有x间客房,可列方程为: .
5. 用150张白铁皮做罐头盒,每张白铁皮可制盒身15个或盒底41个,一个盒身与两个盒底配成一套罐头盒,设把x张白铁皮制盒身,则可列方程为
.
7x+7=9(x-1)
2×15x=41×(150-x)
分层作业
【拓展延伸作业】
6. 现有若干本书分给班上的同学,若每人分5本,则还缺20本;若每人分4本,则剩余25本,则班上有多少名学生?多少本书?
(1)设班上共有.x名同学,根据题意列方程
(2)设共有y本书,根据题意列方程;
(3)选择上面的一种设未知数的方法,解决问题.
解:(1)设班上共有x名同学,
根据题意得:5x-20=4x+25;
(2)设共有y本书,
根据题意得:
分层作业
(3)若选方法一:5x-20=4x+25,
解得:x=45,
所以5x+20=205,
即有45名学生,205本书;
若选方法二:
解得:y=205,
即有205本书,45名学生
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第三章一元一次方程
3.4实际问题与一元一次方程
(第一课时)产品配套问题和工程问题
1.理解配套问题和工程问题的背景.
2.掌握用一元一次方程解决实际问题的基本过程.
3.分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
学习目标
复习提问
一元一次方程的求解步骤是什么?
实例引入
生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
典例解析
例1.某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母. 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
产品类型 生产人数 单人产量 总产量
螺钉 1200
螺母 2000
列表分析:
x
22-x
1200 x
2000(22-x)
螺母总量=螺钉总量×2
提示:这类问题中配套的物品之间具有一定的数量关系,这可以作为列方程的依据.
分析:每天生产的螺母数量是螺钉数量的2倍时,它们刚好配套.
典例解析
解:设应安排x名工人生产螺母,(22-x)名工人生产螺钉.根据螺母数量应是螺钉数量的2倍,列出方程
2×1200(22-x)=2000x
解方程,得 x=12
所以 22-x=10
答:应安排10名工人生产螺钉,12名工人生产螺母.
解法1
典例解析
例1.某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母. 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析:从螺钉的角度来看,螺钉数等于套数;从螺母的角度来看,螺母数等于套数的2倍.可以根据生产的套数是一样的建立方程解决.
列表分析:
产品类型 生产人数 单人产量 总产量 产品套数
螺钉 x 1200
螺母 2000
1200x
22-x
2000(22-x)
1200x
典例解析
解法2
解:设应安排 x 名工人生产螺钉,(22-x)名工人生产螺母.依题意,得
解方程,得 x=10.
所以 2-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
建立模型
方法归纳
解决配套问题的思路:
1.利用配套问题中物品之间具有的数量关系作为列方程的依据;
2.利用配套问题中的套数不变作为列方程的依据.
典例解析
例2.某服装厂要生产一批校服,已知每3m的布料可以做2件上衣或3条裤子,要求一件上衣和两条裤子配一套,现有1008m的布料,应怎样计划用料才能做尽可能多的成套校服 校服有多少套
典例解析
例3.整理一批图书,由一个人做要40h完成.现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
解:设安排x人先做4h. 根据先后两个时段的工作量之和应等于总工作量,列出方程
解得x=2
答:应安排2人先做4h.
随堂练习
1.某防护服厂有54人,每人每天可加工防护服8件或防护面罩10个,已知一件防护服配一个防护面罩,为了使每天生产的防护服与防护面罩正好配套,需要安排多少人生产防护服?
解:设需要安排x人生产防护服,则安排(54-x)人生产防护面罩.
由题意,得8x=10(54-x),
解得x=30.
答:需要安排30人生产防护服.
随堂练习
2.一张方桌由1个桌面、4条桌腿组成,如果1m3木料可以做50个桌面或300条桌腿,现有5m3木料,要使做出的桌面和桌腿恰好配成方桌,应用多少木料来做桌面 能配成多少张方桌
解:设应用xm3木料做桌面,则用(5-x)m3木料做桌腿.
根据题意得50x×4=300(5-x),
解得x=3.
则能配成方桌50×3=150(张).
答:应用3m3木料做桌面,能配成150张方桌.
随堂练习
3.将一段长为1.2km的河道的整治任务交由甲、乙两个工程队接力完成,共用时60天.已知甲队每天整治24m,乙队每天整治16m,则甲队整治河道_______m,乙队整治河道_______m.
4.有一段长为146m的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26m.已知甲工程队每天比乙工程队多掘进2m,按此速度施工,甲、乙两个工程队还需联合工作______天.
720
480
10
随堂练习
5.一项工程,甲单独做10天可以完成,乙单独做15天可以完成,现甲队先做2天,余下的工程由两队共同做x天刚好可以完成,则由题意可列出的方程是___________________.
中考链接
(2017·滨州)某车间有27名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺母16个或螺栓22个,若分配x名工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下面所列方程中正确的是( )
A.22x=16(27-x) B.16x=22(27-x)
C.2×16x=22(27-x) D.2×22x=16(27-x)
D
课堂小结
列方程解决实际问题的一般步骤:
审:审清题意,分清题中的已知量、未知量.
设:设未知数,设其中某个未知量为x.
列:根据题意寻找等量关系列方程.
解:解方程.
验:检验方程的解是否符合题意.
答:写出答案 (包括单位).
当堂测试
1. 某机械厂加工车间有33名工人,平均每名工人每天加工大齿轮5个或小齿轮15个,已知2个大齿轮和3个小齿轮配成一套,问分别安排多少名工人加工大,小齿轮,才能刚好配套?若设加工大齿轮的工人有名,则可列方程是( )
A.2×5(33-x)=3×15x B.2×5x=3×15(33-x)
C.3×5x=2×15(33-x) D.3×5(33-x)=2×15x
2. 2020年,新冠疫情肆虐全球,口罩成了人们出行的“标配”,某口置生产车间有26名工人,每人每天可以生产800个口置面或1000根口置带,1个口置面需要配2根口置带,为了使每天生产口置面和口置带刚好配套,设安排x名工人生产口置面,则下面所列方程正确的是( )
A.1000(26-x)=2×800x B.1000(13-x)=800x
C.2×1000(26-x)=800x D.1000(26-x)=800x
C
A
当堂测试
3. 我国明代数学读本《算法统宗》中有一道题,其题意为;客入一起分银子,若每人6两还剩3两;若每人8两,还差4两,问银子共有几两?没银子共有x两,则可列方程为( )
A,6x+3=8x-4 B.6x-3=8x+4
C. D.
C
当堂测试
4. 众所周知,中华诗词博大精深,集大量的情景情感于短短数十字之间,或豪放,或婉约,或思民生疾苦,或抒发己身豪情逸致,文化价值极高。而数学与古诗词更是有着密切的联系.古诗中,五言绝句是四句诗,每句都是五个字;七言绝句是四句诗,每句都是七个字。有一本诗集,其中五言绝句比七言绝句多13首,总字数却反而少了20个字.问两种诗各多少首?设七言绝句有x首,根据题意,可列方程为 .
5. 元代《算学启蒙》里有这样一道题:“良马日行二百四十里,弩马日行一百五十里,弩马先行十二日,问良马几何追及之?”设良马x天能追上弩马,可列方程为 .
28x-20(x+13)=20
150×12+150x=240x
当堂测试
6. 全班有54人去公园划船,一共租用了10只船.每只大船坐6人,每只小船坐4人,且所有的船刚好坐满.租用的大船,小船各有多少只?
解:设租用的大船x只,则租用的小船(10-x)只,由题意得
6x+4(10-x)=54,
解得:x=7,
10-x=10-7=3(只)
答:租用的大船,小船各有7只和3只
分层作业
【基础达标作业】
1. 为鼓励居民节约用水,某市对居民用水实行“阶梯收费”,规定每户每月用水量不超过10吨,水价为每吨2元;超过10吨的部分每吨3.5元.已知小莉家某月交水费34元,则小莉家该月用水多少吨?若设小莉家该月用水x吨,则可列方程为( )
A.2×10-3.5×(x-10)=34 B.3.5×10+2×(x-10)=34
C.2×10+3.5×(10-x)-34 D.2×10+3.5×(x-10)=34
D
分层作业
2. 随着国力的提升,琳琅满目的消费品开始不断刷新着各阶层人民的满足感,每逢年末,促销手段层出不迭,某超市中,一种商品每件的标价是330元,按标价的八折销售时,可获利10%,设这种商品每件的进价为x元,可列方程为( )
330× =10%x B. 330 x=10%x
C. 330× =(1+10%)x D. x=
B
分层作业
3.我国古代《孙子算经》卷中记载“多人共车”问题,其原文如下:今有三人共车,二车空,二人共车,九人步,问人与车各几何?其大意为:若3个人乘一辆车,则空2辆车;若2个人乘一辆车,则有9个人要步行,问人与车数各是多少?若设有2个人,则可列方程是( )
A.3(x+2)=2x-9 B.3(x+2)=2x-9
C. D.
C
分层作业
【能力提升作业】
4. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,”诗中后面两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.设有x间客房,可列方程为: .
5. 用150张白铁皮做罐头盒,每张白铁皮可制盒身15个或盒底41个,一个盒身与两个盒底配成一套罐头盒,设把x张白铁皮制盒身,则可列方程为
.
7x+7=9(x-1)
2×15x=41×(150-x)
分层作业
【拓展延伸作业】
6. 现有若干本书分给班上的同学,若每人分5本,则还缺20本;若每人分4本,则剩余25本,则班上有多少名学生?多少本书?
(1)设班上共有.x名同学,根据题意列方程
(2)设共有y本书,根据题意列方程;
(3)选择上面的一种设未知数的方法,解决问题.
解:(1)设班上共有x名同学,
根据题意得:5x-20=4x+25;
(2)设共有y本书,
根据题意得:
分层作业
(3)若选方法一:5x-20=4x+25,
解得:x=45,
所以5x+20=205,
即有45名学生,205本书;
若选方法二:
解得:y=205,
即有205本书,45名学生
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
