24.2.2 直线和圆的位置关系(第3课时)课件(共20张PPT)-2023-2024学年九年级数学上册同步精品课堂(人教版)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(第3课时)课件(共20张PPT)-2023-2024学年九年级数学上册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 22:21:30 | ||
图片预览



文档简介
人教版数学九年级上册
第24.2.2直线和圆的位置关系(第3课时)
学习目标
1.掌握切线长的定义及切线长定理.
2.初步学会运用切线长定理进行计算与证明.
3.认识三角形的内切圆及其有关概念,会作一个三角形的内切圆,掌握内心的性质.
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的性质定理:
圆的切线垂直于过切点的半径.
复习引入
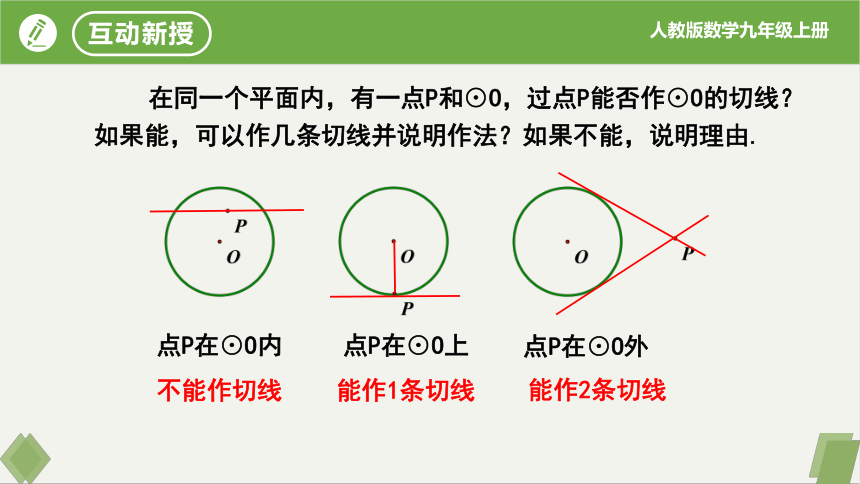
在同一个平面内,有一点P和⊙O,过点P能否作⊙O的切线?如果能,可以作几条切线并说明作法?如果不能,说明理由.
点P在⊙O内
点P在⊙O上
点P在⊙O外
互动新授
不能作切线
能作1条切线
能作2条切线
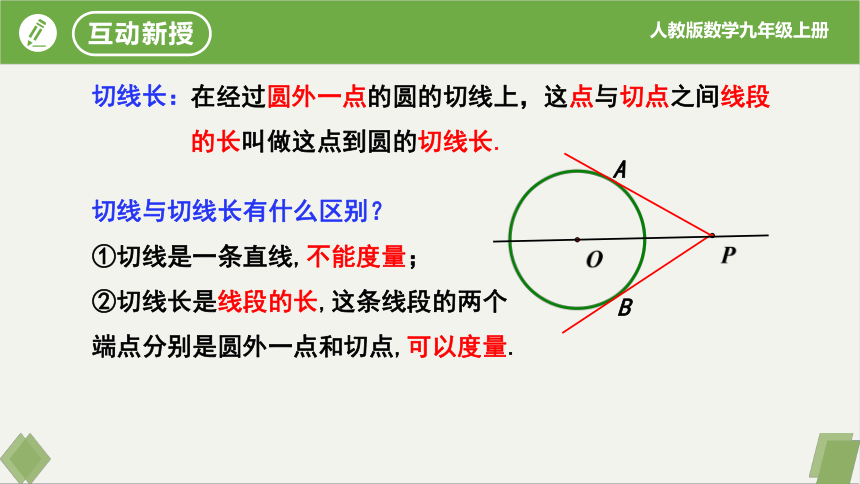
在经过圆外一点的圆的切线上,这点与切点之间线段的长叫做这点到圆的切线长.
切线长:
A
B
互动新授
切线与切线长有什么区别?
①切线是一条直线,不能度量;
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
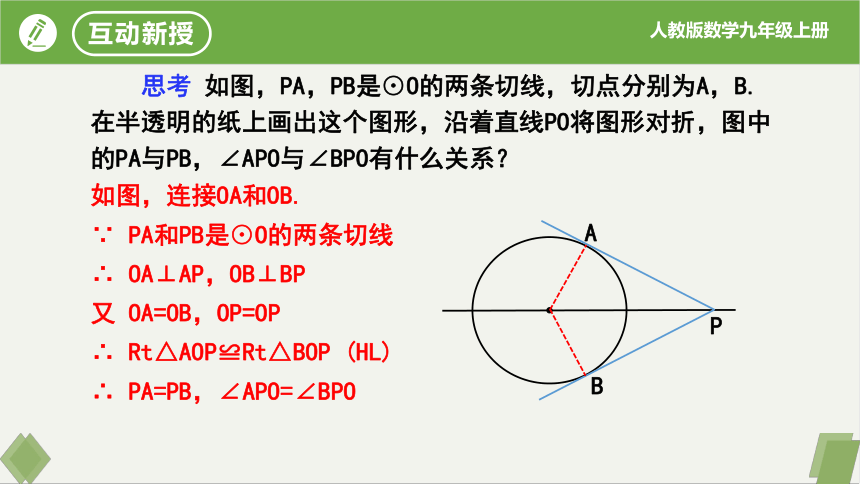
思考 如图,PA,PB是⊙O的两条切线,切点分别为A,B.在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
互动新授
P
A
B
如图,连接OA和OB.
∵ PA和PB是⊙O的两条切线
∴ OA⊥AP,OB⊥BP
又 OA=OB,OP=OP
∴ Rt△AOP≌Rt△BOP (HL)
∴ PA=PB,∠APO=∠BPO
互动新授
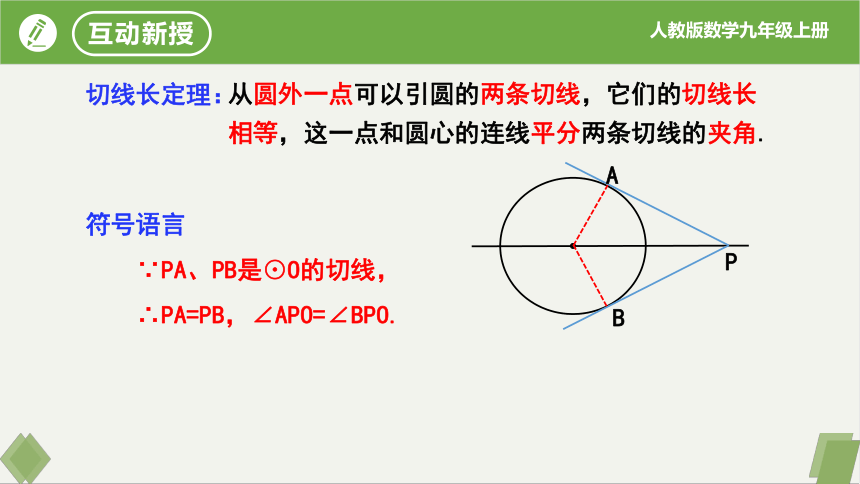
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
P
A
B
符号语言
∵PA、PB是⊙O的切线,
∴PA=PB,∠APO=∠BPO.
切线长定理:
互动新授
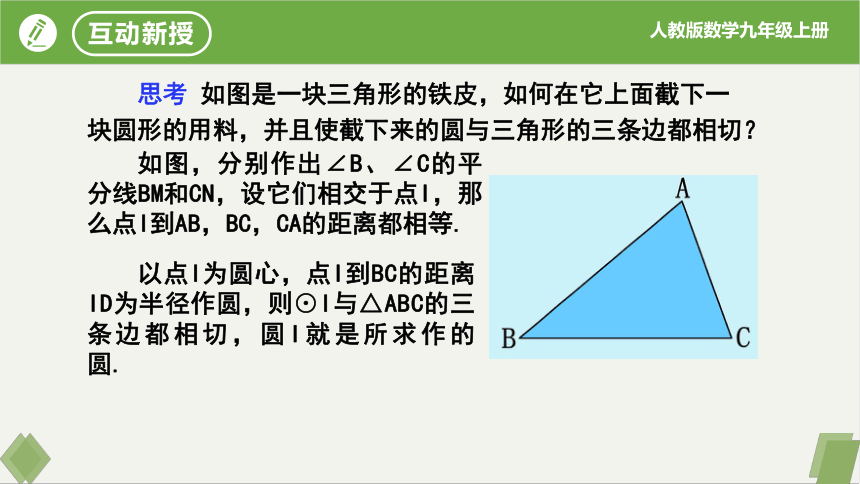
如图,分别作出∠B、∠C的平分线BM和CN,设它们相交于点I,那么点I到AB,BC,CA的距离都相等.
以点I为圆心,点I到BC的距离ID为半径作圆,则⊙I与△ABC的三条边都相切,圆I就是所求作的圆. ?
思考 如图是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切?
互动新授
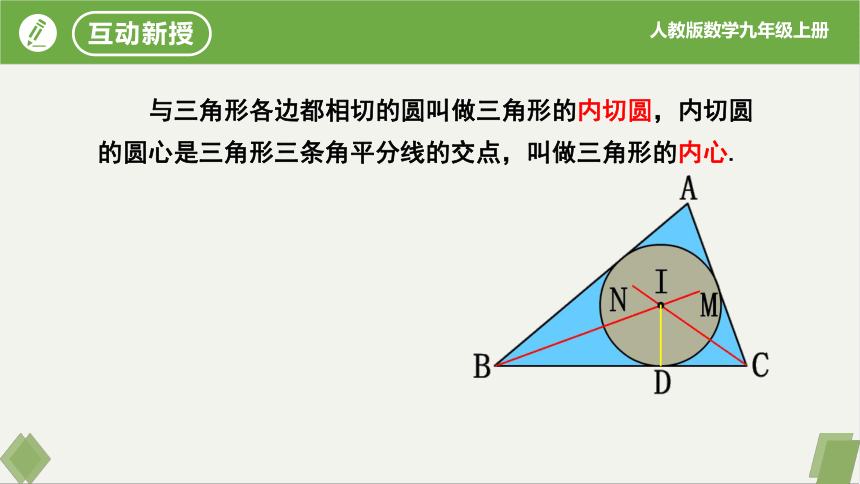
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
例2 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13.求AF、BD、CE的长.
解:设AF=x,则AE=x,CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x
由BD+CD=BC,可得(13-x)+(9-x)=14
解得 x=4
因此 AF=4,BD=5,CE=9.
典例精析
1.如图,????????、????????、????????是⊙????的切线,????、????、????是切点,????????分别交????????、????????于????、????两点.如--∠????????????=????????°,则∠????????????的度数为( )
A.????????° B.???????? C.????????° D.????????°
2.如图,PA,PB分别与⊙O相切于A、B两点.直线EF切⊙O于C点,分别交PA、PB于E、F,且PA=10.则△PEF的周长为( )
A.10 B.15 C.20 D.25
?
C
C
小试牛刀
B
P
O
A
3.PA、PB是☉O的两条切线,A,B是切点,OA=3.
(1)若AP=4,则OP= ;
(2)若∠BPA=60?,则OP= .
5
6
小试牛刀
1.如图,△ABC的内切圆分别和BC,AC,AB切于D,E,F;
如果AF=2,BD=7,CE=4,则BC= ,AC= ,AB= .
2.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8cm,则△PDE的周长为______.
11
6
9
A
C
F
E
7
4
B
D
2
O
A
P
D
C
B
E
O
16cm
课堂检测
3.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,
(1)若∠CBD=34°,求∠BEC的度数;(2)求证:DE=DB.
解:(1)∵∠CBD=34°
∴∠CAD=34°
∵点E是△ABC的的内心∴∠BAC=2∠CAD=68°
∴∠EBC+∠ECB=(180°-68°)÷2=56°
∴∠BEC=180°-56°=124°
课堂检测
3.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,
(1)若∠CBD=34°,求∠BEC的度数;(2)求证:DE=DB.
(2)∵E是△ABC的内心
∴∠BAD=∠CAD,∠EBA=∠EBC
∵ ∠DEB=∠BAD+∠EBA,∠DBE=∠EBC+∠CBD,∠CBD=∠CAD
∴∠DEB=∠DBE
∴DE=DB .
课堂检测
1.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连结CD.求证:OD=CD.
证明:如图,连接OC,
∵点O是△ABC的内心,
∴∠CAD=∠BAD,∠OCA=∠OCB,
∵∠BAD=∠BCD,
∴∠COD=∠CAD+∠OCA=∠BAD+∠OCB,
∠DCO=∠BCD+∠OCB,
∴∠COD=∠DCO,
∴△DCO是等腰三角形,
∴OD=CD.
拓展训练
课堂小结
1.如图,从☉O外一点P引的两条切线PA、PB,切点分别为A、B.如∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4???? D.8????
2.如图,四边形ABCD的边AB,BC,CD,DA和☉O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD等于( )
A.5 B.8 C.10 D.12
?
B
C
课后作业
3.如图,⊙O是△ABC的内切圆,切点分别为D,E,F,∠B=60°,∠C=70°,求∠EDF的度数.
A
B
C
O
D
E
F
解:连接OE,OF,在△ABC中,
∠A=180°- (∠B+∠C)
=180°- (60°+70°)=50°
∵⊙O是△ABC的内切圆,
∴AB⊥OF,AC⊥OE.
在四边形AFOE中,
∠EOF=360°-(∠A+∠AFO+∠AEO)
=360°-(50°+90°+90°)=130°
课后作业
谢谢聆听
第24.2.2直线和圆的位置关系(第3课时)
学习目标
1.掌握切线长的定义及切线长定理.
2.初步学会运用切线长定理进行计算与证明.
3.认识三角形的内切圆及其有关概念,会作一个三角形的内切圆,掌握内心的性质.
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的性质定理:
圆的切线垂直于过切点的半径.
复习引入
在同一个平面内,有一点P和⊙O,过点P能否作⊙O的切线?如果能,可以作几条切线并说明作法?如果不能,说明理由.
点P在⊙O内
点P在⊙O上
点P在⊙O外
互动新授
不能作切线
能作1条切线
能作2条切线
在经过圆外一点的圆的切线上,这点与切点之间线段的长叫做这点到圆的切线长.
切线长:
A
B
互动新授
切线与切线长有什么区别?
①切线是一条直线,不能度量;
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
思考 如图,PA,PB是⊙O的两条切线,切点分别为A,B.在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
互动新授
P
A
B
如图,连接OA和OB.
∵ PA和PB是⊙O的两条切线
∴ OA⊥AP,OB⊥BP
又 OA=OB,OP=OP
∴ Rt△AOP≌Rt△BOP (HL)
∴ PA=PB,∠APO=∠BPO
互动新授
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
P
A
B
符号语言
∵PA、PB是⊙O的切线,
∴PA=PB,∠APO=∠BPO.
切线长定理:
互动新授
如图,分别作出∠B、∠C的平分线BM和CN,设它们相交于点I,那么点I到AB,BC,CA的距离都相等.
以点I为圆心,点I到BC的距离ID为半径作圆,则⊙I与△ABC的三条边都相切,圆I就是所求作的圆. ?
思考 如图是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切?
互动新授
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
例2 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13.求AF、BD、CE的长.
解:设AF=x,则AE=x,CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x
由BD+CD=BC,可得(13-x)+(9-x)=14
解得 x=4
因此 AF=4,BD=5,CE=9.
典例精析
1.如图,????????、????????、????????是⊙????的切线,????、????、????是切点,????????分别交????????、????????于????、????两点.如--∠????????????=????????°,则∠????????????的度数为( )
A.????????° B.???????? C.????????° D.????????°
2.如图,PA,PB分别与⊙O相切于A、B两点.直线EF切⊙O于C点,分别交PA、PB于E、F,且PA=10.则△PEF的周长为( )
A.10 B.15 C.20 D.25
?
C
C
小试牛刀
B
P
O
A
3.PA、PB是☉O的两条切线,A,B是切点,OA=3.
(1)若AP=4,则OP= ;
(2)若∠BPA=60?,则OP= .
5
6
小试牛刀
1.如图,△ABC的内切圆分别和BC,AC,AB切于D,E,F;
如果AF=2,BD=7,CE=4,则BC= ,AC= ,AB= .
2.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8cm,则△PDE的周长为______.
11
6
9
A
C
F
E
7
4
B
D
2
O
A
P
D
C
B
E
O
16cm
课堂检测
3.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,
(1)若∠CBD=34°,求∠BEC的度数;(2)求证:DE=DB.
解:(1)∵∠CBD=34°
∴∠CAD=34°
∵点E是△ABC的的内心∴∠BAC=2∠CAD=68°
∴∠EBC+∠ECB=(180°-68°)÷2=56°
∴∠BEC=180°-56°=124°
课堂检测
3.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,
(1)若∠CBD=34°,求∠BEC的度数;(2)求证:DE=DB.
(2)∵E是△ABC的内心
∴∠BAD=∠CAD,∠EBA=∠EBC
∵ ∠DEB=∠BAD+∠EBA,∠DBE=∠EBC+∠CBD,∠CBD=∠CAD
∴∠DEB=∠DBE
∴DE=DB .
课堂检测
1.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连结CD.求证:OD=CD.
证明:如图,连接OC,
∵点O是△ABC的内心,
∴∠CAD=∠BAD,∠OCA=∠OCB,
∵∠BAD=∠BCD,
∴∠COD=∠CAD+∠OCA=∠BAD+∠OCB,
∠DCO=∠BCD+∠OCB,
∴∠COD=∠DCO,
∴△DCO是等腰三角形,
∴OD=CD.
拓展训练
课堂小结
1.如图,从☉O外一点P引的两条切线PA、PB,切点分别为A、B.如∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4???? D.8????
2.如图,四边形ABCD的边AB,BC,CD,DA和☉O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD等于( )
A.5 B.8 C.10 D.12
?
B
C
课后作业
3.如图,⊙O是△ABC的内切圆,切点分别为D,E,F,∠B=60°,∠C=70°,求∠EDF的度数.
A
B
C
O
D
E
F
解:连接OE,OF,在△ABC中,
∠A=180°- (∠B+∠C)
=180°- (60°+70°)=50°
∵⊙O是△ABC的内切圆,
∴AB⊥OF,AC⊥OE.
在四边形AFOE中,
∠EOF=360°-(∠A+∠AFO+∠AEO)
=360°-(50°+90°+90°)=130°
课后作业
谢谢聆听
同课章节目录
