第五单元第3课时 间隔排列(教学课件)-三年级数学上册同步高效课堂 苏教版(共33张PPT)
文档属性
| 名称 | 第五单元第3课时 间隔排列(教学课件)-三年级数学上册同步高效课堂 苏教版(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
小学数学·三年级(上)·SJ
5.3 间隔排列
在探索活动中初步培养分析、比较、综合和归纳的能力。
经历一一间隔排列的两种物体个数之间关系的探索过程,体会其中蕴含的简单数学规律。
在发现规律的过程中,感受数学与生活的联系,学会与他人合作交流。
用数学眼光观察周围事物,从数学角度分析生活现象的初步意识和能力,获得积极地数学学习情感。
用恰当的方式描述、表达规律。
经历“一一间隔排列”中简单规律的探索过程。
小朋友们排队入场,你知道下一个进来是男孩还是女孩吗?
你是怎么判断的?
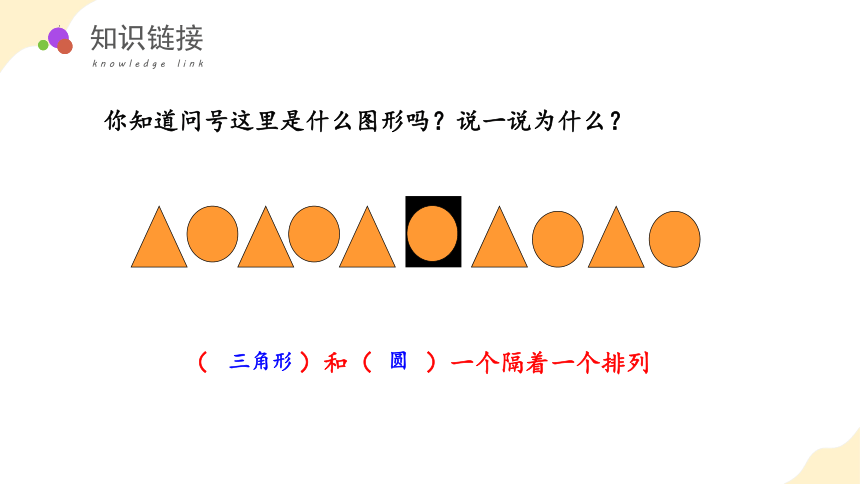
你知道问号这里是什么图形吗?说一说为什么?
?
( )和( )一个隔着一个排列
三角形
圆
合作探究两端物体相同的间隔排列规律。
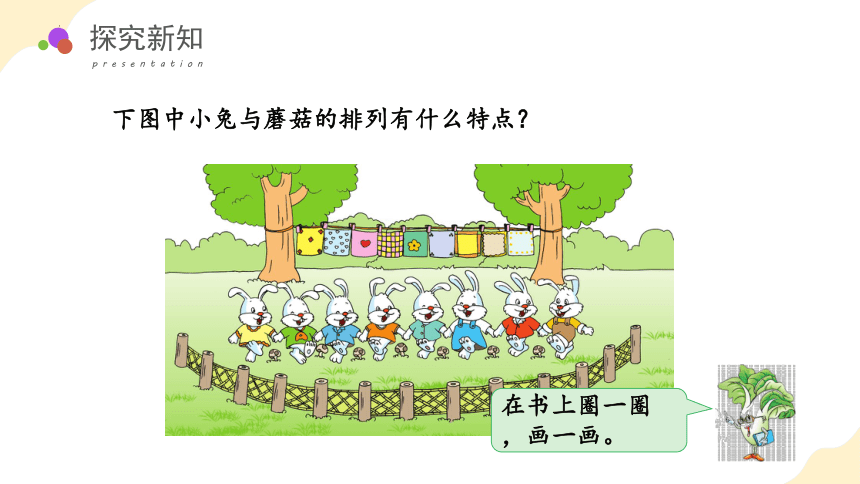
下图中小兔与蘑菇的排列有什么特点?
在书上圈一圈,画一画。
小兔与蘑菇是一个隔着一个排列。像这样的排列规律,数学上称为——间隔排列。
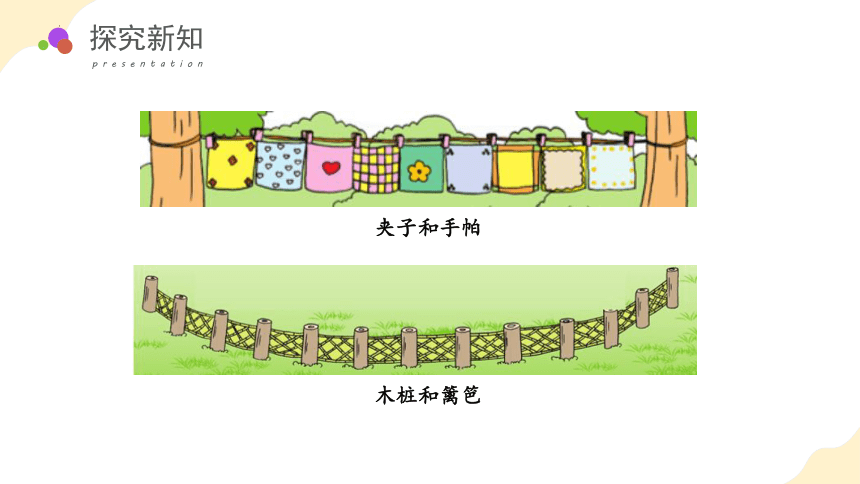
图片中还有“一一间隔排列”的例子吗?
夹子和手帕
木桩和篱笆
比较每排两种物体的数量,和同学交流你的发现。
这几组数据有什么规律吗?
8
7
13
12
10
9
为什么每排两种物体的数量都相差1呢?
把一只兔子和一个蘑菇看成一组,一一对应地分组,最后余下一个是( )。我们就可以发现,两端都是兔子时,它的数量就比中间的蘑菇多( )个。
小兔
1
把一只夹子和一个手帕看成一组,一一对应地分组,最后余下一个是( )。我们就可以发现,两端都是兔子时,它的数量就比中间的蘑菇多( )个。
夹子
1
把一只木桩和一个篱笆看成一组,一一对应地分组,最后余下一个是( )。我们就可以发现,两端都是兔子时,它的数量就比中间的蘑菇多( )个。
木桩
1
归纳
两种物体一一间隔排列,如果两端物体相同,那么两端物体个数比中间物体个数多1。
数量关系式:
两端物体个数-1=中间物体个数
中间物体个数+1=两端物体个数
合作探究两端物体不同的间隔排列规律。
摆一摆、画一画:
如果把 与 一个隔一个地排成一行,如果 有10个, 最少需要几个?最多有几个呢?请你边摆边画出来。
1. 两端都是正方形时:正方形的个数就比圆形多一个
2. 两端都是圆形时:圆形的个数就比正方形多一个
3. 两端不同时:正方形的个数和圆形的个数相等
最少8个
最多11个
两种物体间隔排列成一圈,两种物体的数量相等。
快乐的跳舞:
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
2
两种物体一个隔一个地排成一行,它们的数量可能相等,也可能相差1。
一组一组地圈一圈,容易发现间隔排列物体间的数量关系。
生活中有很多规律,要仔细观察、认真思考才能发现。
回顾探索和发现规律的过程,说说你的体会。
当两种物体:一一间隔排列
归纳
两端相同
两端不同
围成一圈
两端物体比中间物体多一个
两种物体数量相同
1. 20 只小兔站成一排,每两只小兔中间有一个蘑菇,一共有多少个蘑菇?
小兔是两端物体,蘑菇是中间物体,蘑菇比小兔少1。
20-1=19(个)
答:一共有19个蘑菇。
2. 把 20 块手帕像上面那样夹在绳子上,一共需要多少个夹子?
夹子是两端物体,手帕是中间物体,手帕比夹子少1。
20+1=21(个)
答:一共需要21个夹子。
3. 6个小朋友排成一排做操,相邻2人间隔3米,这个队伍长多少米?
6-1=5(个)
3×5=15(米)
答: 这个队伍长15米。
4.在圆形花坛外侧每隔3米打一个木桩,刚好打下34个木桩,那么花坛外侧长多少米?
34×3=102(米)
答:花坛外侧长102米。
5.一条马路长60米,在马路的两侧装路灯,一侧每隔5米装1盏,从路头装到路尾。一共要装多少盏路灯?
60÷5=12( 个)
12+1=13(盏)
13×2=26(盏)
答:一共要装26盏路灯。
今天你学会了什么?
你是怎么学会的?
当两种物体一一间隔排列时:
当两端相同时
当两端不同时
两种物体的数量相差1
两种物体的数量相等
当围成一圈时
两种物体的数量相等
自我评价
内容 评价等级 A B C
学习态度
学习自信
学习合作
小组互评
内容 评价等级 A B C
学习态度
学习自信
学习合作
小学数学·三年级(上)·SJ
5.3 间隔排列
在探索活动中初步培养分析、比较、综合和归纳的能力。
经历一一间隔排列的两种物体个数之间关系的探索过程,体会其中蕴含的简单数学规律。
在发现规律的过程中,感受数学与生活的联系,学会与他人合作交流。
用数学眼光观察周围事物,从数学角度分析生活现象的初步意识和能力,获得积极地数学学习情感。
用恰当的方式描述、表达规律。
经历“一一间隔排列”中简单规律的探索过程。
小朋友们排队入场,你知道下一个进来是男孩还是女孩吗?
你是怎么判断的?
你知道问号这里是什么图形吗?说一说为什么?
?
( )和( )一个隔着一个排列
三角形
圆
合作探究两端物体相同的间隔排列规律。
下图中小兔与蘑菇的排列有什么特点?
在书上圈一圈,画一画。
小兔与蘑菇是一个隔着一个排列。像这样的排列规律,数学上称为——间隔排列。
图片中还有“一一间隔排列”的例子吗?
夹子和手帕
木桩和篱笆
比较每排两种物体的数量,和同学交流你的发现。
这几组数据有什么规律吗?
8
7
13
12
10
9
为什么每排两种物体的数量都相差1呢?
把一只兔子和一个蘑菇看成一组,一一对应地分组,最后余下一个是( )。我们就可以发现,两端都是兔子时,它的数量就比中间的蘑菇多( )个。
小兔
1
把一只夹子和一个手帕看成一组,一一对应地分组,最后余下一个是( )。我们就可以发现,两端都是兔子时,它的数量就比中间的蘑菇多( )个。
夹子
1
把一只木桩和一个篱笆看成一组,一一对应地分组,最后余下一个是( )。我们就可以发现,两端都是兔子时,它的数量就比中间的蘑菇多( )个。
木桩
1
归纳
两种物体一一间隔排列,如果两端物体相同,那么两端物体个数比中间物体个数多1。
数量关系式:
两端物体个数-1=中间物体个数
中间物体个数+1=两端物体个数
合作探究两端物体不同的间隔排列规律。
摆一摆、画一画:
如果把 与 一个隔一个地排成一行,如果 有10个, 最少需要几个?最多有几个呢?请你边摆边画出来。
1. 两端都是正方形时:正方形的个数就比圆形多一个
2. 两端都是圆形时:圆形的个数就比正方形多一个
3. 两端不同时:正方形的个数和圆形的个数相等
最少8个
最多11个
两种物体间隔排列成一圈,两种物体的数量相等。
快乐的跳舞:
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
2
两种物体一个隔一个地排成一行,它们的数量可能相等,也可能相差1。
一组一组地圈一圈,容易发现间隔排列物体间的数量关系。
生活中有很多规律,要仔细观察、认真思考才能发现。
回顾探索和发现规律的过程,说说你的体会。
当两种物体:一一间隔排列
归纳
两端相同
两端不同
围成一圈
两端物体比中间物体多一个
两种物体数量相同
1. 20 只小兔站成一排,每两只小兔中间有一个蘑菇,一共有多少个蘑菇?
小兔是两端物体,蘑菇是中间物体,蘑菇比小兔少1。
20-1=19(个)
答:一共有19个蘑菇。
2. 把 20 块手帕像上面那样夹在绳子上,一共需要多少个夹子?
夹子是两端物体,手帕是中间物体,手帕比夹子少1。
20+1=21(个)
答:一共需要21个夹子。
3. 6个小朋友排成一排做操,相邻2人间隔3米,这个队伍长多少米?
6-1=5(个)
3×5=15(米)
答: 这个队伍长15米。
4.在圆形花坛外侧每隔3米打一个木桩,刚好打下34个木桩,那么花坛外侧长多少米?
34×3=102(米)
答:花坛外侧长102米。
5.一条马路长60米,在马路的两侧装路灯,一侧每隔5米装1盏,从路头装到路尾。一共要装多少盏路灯?
60÷5=12( 个)
12+1=13(盏)
13×2=26(盏)
答:一共要装26盏路灯。
今天你学会了什么?
你是怎么学会的?
当两种物体一一间隔排列时:
当两端相同时
当两端不同时
两种物体的数量相差1
两种物体的数量相等
当围成一圈时
两种物体的数量相等
自我评价
内容 评价等级 A B C
学习态度
学习自信
学习合作
小组互评
内容 评价等级 A B C
学习态度
学习自信
学习合作
同课章节目录
- 一 两、三位数乘一位数
- 整十、整百数乘一位数的口算
- 倍的认识和有关倍的简单实际问题
- 两、三位数乘一位数(不进位)的笔算
- 两、三位数乘一位数(进位)的笔算
- 两、三位数乘一位数(连续进位)的笔算
- 乘数中间、末尾有0的乘法
- 二 千克和克
- 认识千克
- 认识克
- 三 长方形和正方形
- 长方形和正方形的基本特征
- 认识周长
- 长方形和正方形周长的计算
- 周长是多少
- 四 两、三位数除以一位数
- 两、三位数除以一位数的口算
- 两、三位数除以一位数(首位能整除)的笔算
- 除法的验算
- 两、三位数除以一位数(首位不能整除)的笔算
- 商中间、末尾有0的除法
- 五 解决问题的策略
- 间隔排列
- 六 平移、旋转和轴对称
- 七 分数的初步认识(一)
- 多彩的“分数条”
