6.5 不规则图形的面积(教学课件)五年级数学上册人教版(共21张PPT)
文档属性
| 名称 | 6.5 不规则图形的面积(教学课件)五年级数学上册人教版(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 08:12:25 | ||
图片预览





文档简介
(共21张PPT)
第六单元 多边形的面积
第五课时
不规则图形的面积
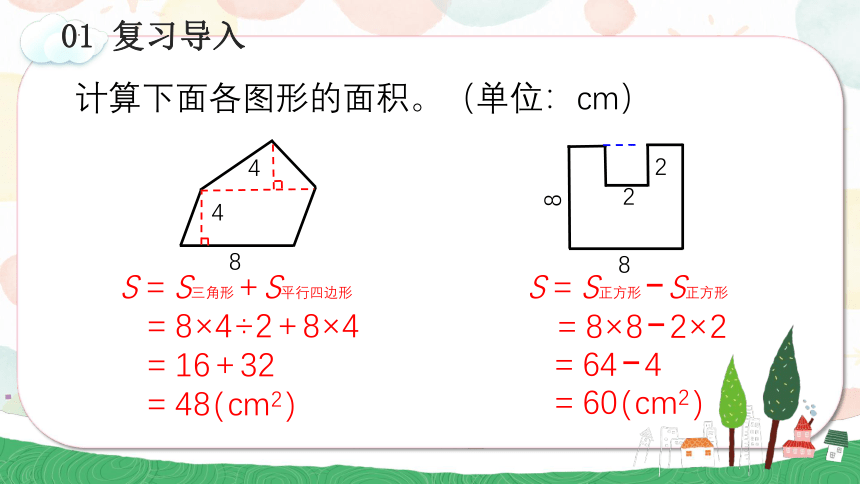
计算下面各图形的面积。(单位:cm)
S=S三角形+S平行四边形
=8×4÷2+8×4
=48(cm2)
=16+32
S=S正方形 S正方形
=8×8 2×2
=60(cm2)
=64 4
8
8
2
2
8
4
4
01 复习导入
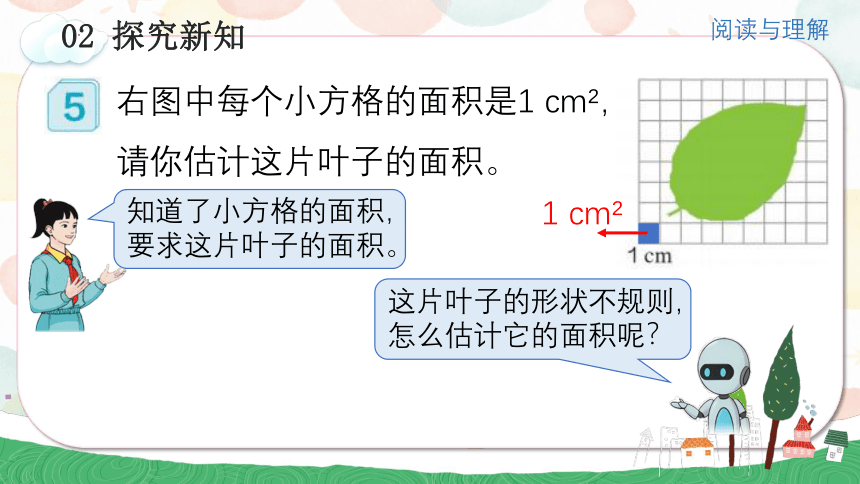
右图中每个小方格的面积是1 cm ,
请你估计这片叶子的面积。
02 探究新知
阅读与理解
你发现了什么?
右图中每个小方格的面积是1 cm ,
请你估计这片叶子的面积。
知道了小方格的面积, 要求这片叶子的面积。
这片叶子的形状不规则,怎么估计它的面积呢?
1 cm
02 探究新知
阅读与理解
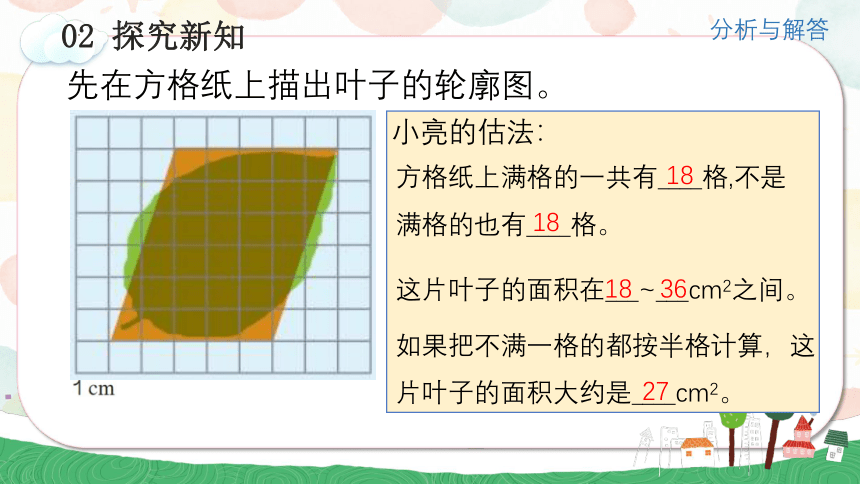
先在方格纸上描出叶子的轮廓图。
02 探究新知
分析与解答
小亮的估法:
方格纸上满格的一共有____格,不是满格的也有____格。
18
18
这片叶子的面积在___~___cm2之间。
18
36
如果把不满一格的都按半格计算,这片叶子的面积大约是____cm2。
27
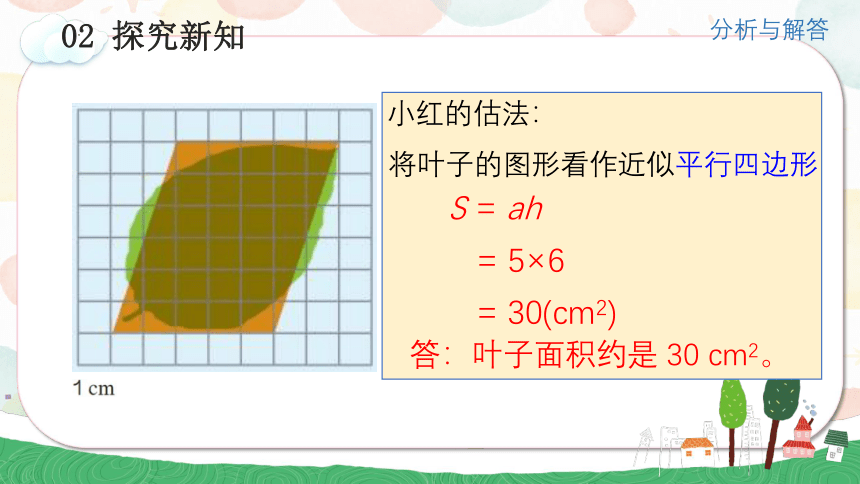
小红的估法:
S = ah
= 5×6
= 30(cm2)
02 探究新知
将叶子的图形看作近似平行四边形
答:叶子面积约是 30 cm2。
分析与解答
如何估计不规则图形的面积?
不规则图形的面积可以转化为学过的图形来估算。
可先通过数方格确定面积的范围,再估算图形的面积。
02 探究新知
回顾与反思
1.有一块地近似平行四边形,形状如右图。这块地的面积约是多少平方米?(得数保留整数。)
03 课堂练行四边形: 43×20.1 ≈ 864(m2)
答:这块地的面积约是864 m2。
(可看成平行四边形计算。)
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
03 课堂练习
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
S三角形: 5×4÷2 = 10(cm2)
S梯 形:(5+2)×4÷2 = 14(cm2)
S涂色部分:10+14 = 24(cm2)
答:涂色部分的面积是24 cm2。
(可将图形分成一个三角形和一个梯形进行计算)
1 cm
03 课堂练习
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
S满格: 8×3+4 = 28(cm2)
答:涂色部分面积大约是 32 cm2。
1
2
3
4
5
6
7
8
8
8
1
2
3
4
1
2
3
4
5
6
7
8
S不满格: 8÷2 = 4(cm2)
S 总: 28+4 = 32(cm2)
方法一:数方格
03 课堂练习
(可以通过数方格计算。)
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
S长方形: 8×4 = 32(cm2)
答:涂色部分面积大约是 32 cm2。
方法二:转化成长方形
03 课堂练习
(可以通过转化成长方形计算。)
8 cm
4 cm
3.一个池塘的形状如下图(涂色部分),图中每个小方格的面积是1m2,请你估计这个池塘的面积。
S = ab
= 12×9
=108(m2)
答:这个池塘的面积大约是108 m2。
03 课堂练习
(可以通过数方格或转化成长方形计算。)
9
12
03 课堂练习
4.利用方格纸估计自己手掌的面积。
20+21÷2=30.5(格)
5.校园里有一块长方形的空地,想种上红花、黄花和绿草。一种设计方案如右图。
(1)你能分别计算出红花、黄花、绿草的种植面积吗
03 课堂练习
(2)请你也设计一种方案,用上我们学过的图形,并计算出每种植物的种植面积。
5.校园里有一块长方形的空地,想种上红花、黄花和绿草。一种设计方案如右图。
(1)你能分别计算出红花、黄花、绿草的种植面积吗
03 课堂练习
S绿草:(18÷2)×(12÷2)÷2×4=108(m2)
黄花和红花面积相等:(18×12-108)÷2=54(m2)
答:红花、黄花、绿草的种植面积分别是 54 m2 、54 m2 、108 m2。
5.校园里有一块长方形的空地,想种上红花、黄花和绿草。一种设计方案如右图。
(2)请你也设计一种方案,用上我们学过的图形,并计算出每种植物的种植面积。
03 课堂练习
S梯形=(a+b)×h÷2
=(2×3+5×3)×(4×3)÷2
=21×12 ÷2
=126(m2)
6.估算右面土地的面积。
答:土地的面积大约是126 m2 。
3 m
3 m
03 课堂练习
(可转化成梯形来计算。)
04 课堂小结
这节课有什么收获呢?
不规则图形的面积
估算不规则图形的面积,可以通过数方格方法确定出不规则图形面积的范围,再估算出其面积的大小;也可以将不规则图形的面积转化为与它形状相近的已学过的图形来估算。
课后作业
1.完成对应的课时的练习;
2.从课时练中选取。
下课啦
同学们
第六单元 多边形的面积
第五课时
不规则图形的面积
计算下面各图形的面积。(单位:cm)
S=S三角形+S平行四边形
=8×4÷2+8×4
=48(cm2)
=16+32
S=S正方形 S正方形
=8×8 2×2
=60(cm2)
=64 4
8
8
2
2
8
4
4
01 复习导入
右图中每个小方格的面积是1 cm ,
请你估计这片叶子的面积。
02 探究新知
阅读与理解
你发现了什么?
右图中每个小方格的面积是1 cm ,
请你估计这片叶子的面积。
知道了小方格的面积, 要求这片叶子的面积。
这片叶子的形状不规则,怎么估计它的面积呢?
1 cm
02 探究新知
阅读与理解
先在方格纸上描出叶子的轮廓图。
02 探究新知
分析与解答
小亮的估法:
方格纸上满格的一共有____格,不是满格的也有____格。
18
18
这片叶子的面积在___~___cm2之间。
18
36
如果把不满一格的都按半格计算,这片叶子的面积大约是____cm2。
27
小红的估法:
S = ah
= 5×6
= 30(cm2)
02 探究新知
将叶子的图形看作近似平行四边形
答:叶子面积约是 30 cm2。
分析与解答
如何估计不规则图形的面积?
不规则图形的面积可以转化为学过的图形来估算。
可先通过数方格确定面积的范围,再估算图形的面积。
02 探究新知
回顾与反思
1.有一块地近似平行四边形,形状如右图。这块地的面积约是多少平方米?(得数保留整数。)
03 课堂练行四边形: 43×20.1 ≈ 864(m2)
答:这块地的面积约是864 m2。
(可看成平行四边形计算。)
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
03 课堂练习
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
S三角形: 5×4÷2 = 10(cm2)
S梯 形:(5+2)×4÷2 = 14(cm2)
S涂色部分:10+14 = 24(cm2)
答:涂色部分的面积是24 cm2。
(可将图形分成一个三角形和一个梯形进行计算)
1 cm
03 课堂练习
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
S满格: 8×3+4 = 28(cm2)
答:涂色部分面积大约是 32 cm2。
1
2
3
4
5
6
7
8
8
8
1
2
3
4
1
2
3
4
5
6
7
8
S不满格: 8÷2 = 4(cm2)
S 总: 28+4 = 32(cm2)
方法一:数方格
03 课堂练习
(可以通过数方格计算。)
2.下图中每个小方格的面积为1 cm2,计算涂色部分的面积。
S长方形: 8×4 = 32(cm2)
答:涂色部分面积大约是 32 cm2。
方法二:转化成长方形
03 课堂练习
(可以通过转化成长方形计算。)
8 cm
4 cm
3.一个池塘的形状如下图(涂色部分),图中每个小方格的面积是1m2,请你估计这个池塘的面积。
S = ab
= 12×9
=108(m2)
答:这个池塘的面积大约是108 m2。
03 课堂练习
(可以通过数方格或转化成长方形计算。)
9
12
03 课堂练习
4.利用方格纸估计自己手掌的面积。
20+21÷2=30.5(格)
5.校园里有一块长方形的空地,想种上红花、黄花和绿草。一种设计方案如右图。
(1)你能分别计算出红花、黄花、绿草的种植面积吗
03 课堂练习
(2)请你也设计一种方案,用上我们学过的图形,并计算出每种植物的种植面积。
5.校园里有一块长方形的空地,想种上红花、黄花和绿草。一种设计方案如右图。
(1)你能分别计算出红花、黄花、绿草的种植面积吗
03 课堂练习
S绿草:(18÷2)×(12÷2)÷2×4=108(m2)
黄花和红花面积相等:(18×12-108)÷2=54(m2)
答:红花、黄花、绿草的种植面积分别是 54 m2 、54 m2 、108 m2。
5.校园里有一块长方形的空地,想种上红花、黄花和绿草。一种设计方案如右图。
(2)请你也设计一种方案,用上我们学过的图形,并计算出每种植物的种植面积。
03 课堂练习
S梯形=(a+b)×h÷2
=(2×3+5×3)×(4×3)÷2
=21×12 ÷2
=126(m2)
6.估算右面土地的面积。
答:土地的面积大约是126 m2 。
3 m
3 m
03 课堂练习
(可转化成梯形来计算。)
04 课堂小结
这节课有什么收获呢?
不规则图形的面积
估算不规则图形的面积,可以通过数方格方法确定出不规则图形面积的范围,再估算出其面积的大小;也可以将不规则图形的面积转化为与它形状相近的已学过的图形来估算。
课后作业
1.完成对应的课时的练习;
2.从课时练中选取。
下课啦
同学们
