19.3 正方形 课件(共23张PPT)2022-2023学年华东师大版数学八年级下册
文档属性
| 名称 | 19.3 正方形 课件(共23张PPT)2022-2023学年华东师大版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 815.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
19.3 正方形
华师大版数学八年级下册
第十九章 矩形,菱形,正方形
复习旧知
1.叙述平行四边形、矩形、菱形的定义和它们的特殊性质.
2.说一说平行四边形、矩形、菱形的内在联系.
情景导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
思考
你能从这个变化过程中给正方形下定义吗
有一个角是直角的菱形叫做正方形。
有一组邻边相等的矩形叫做正方形。
有一个角是直角一组邻边相等的平行四边形叫做正方形。
是直角
有一个角
边相等
有一组邻
边相等
有一组邻
是直角
有一个角
探究新知
由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.如图.
想一想
正方形是菱形吗?正方形具有哪些性质
正方形是特殊的菱形,它具有平行四边形、矩形、菱形的一切性质。
边:对边平行,四边都相等。
角:四个角都是直角
对角线:对角线相等且互相垂直平分
A
B
C
D
O
思考
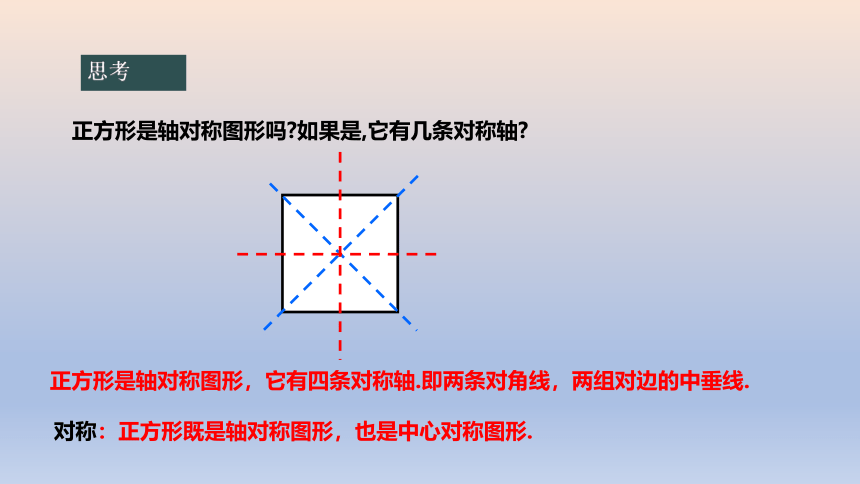
正方形是轴对称图形吗 如果是,它有几条对称轴
正方形是轴对称图形,它有四条对称轴.即两条对角线,两组对边的中垂线.
对称:正方形既是轴对称图形,也是中心对称图形.
归纳总结
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
典例精析
A
C
D
B
O
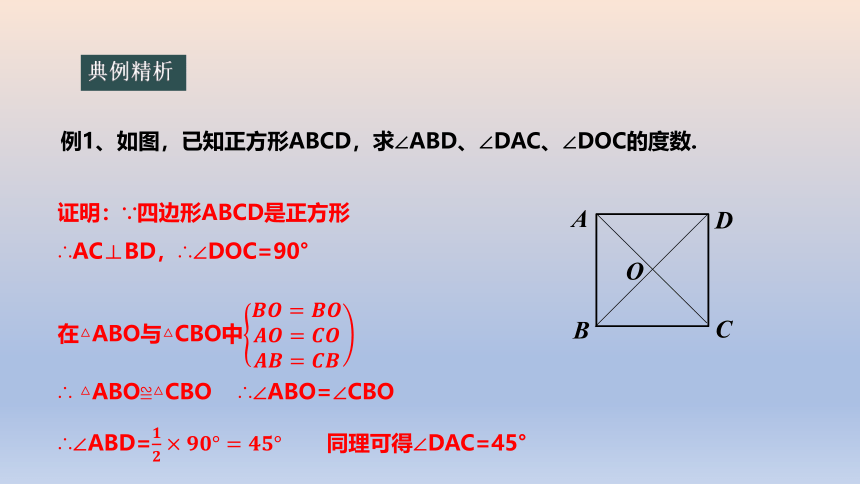
例1、如图,已知正方形ABCD,求∠ABD、∠DAC、∠DOC的度数.
证明:∵四边形ABCD是正方形
∴AC⊥BD,∴∠DOC=90°
在△ABO与△CBO中
∴ △ABO≌△CBO ∴∠ABO=∠CBO
∴∠ABD= 同理可得∠DAC=45°
A
D
C
B
O
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
变式训练
探究新知
从图中可看出,
⑴在正方形中产生了哪些特殊图形?
⑵产生了哪些特殊角?
D
O
A
B
C
450
450
450
450
450
450
450
450
4个全等的小等腰直角三角形和4个全等的大等腰直角三角形.
900和450
正方形图形“庐山真面目”
思考
怎样判定一个矩形是正方形?怎样判定一个菱形是正方形?
怎样判定一个平行四边形是正方形?
探究新知
1 .定义法:
2.矩形法:
4.对角线法:
一邻边相等
一个直角
+
+
平行四边形
=
正方形
3.菱形法:
一邻边相等
+
矩形
=
正方形
一个直角
+
菱形
=
正方形
互相平分
+
互相垂直
相等
+
=
正方形
① 对角线相等的菱形是正方形 ( )
② 对角线互相垂直的矩形是正方形 ( )
③ 对角线互相垂直且相等的四边形是正方形 ( )
④ 四条边都相等的四边形是正方形 ( )
⑤ 四个角都相等的四边形是正方形 ( )
⑥ 四边相等,有一个角是直角的四边形是正方形.( )
判断对错
√
√
×
×
×
√
对应训练
典例精析
例、在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
典例精析
如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
证明:∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,∴四边形EDFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线 DE⊥AC,DG⊥AB,
∴ DE=DG. 同理得DG=DF,
∴ED=DF, ∴矩形EDFC是正方形.
变式训练
课堂练习
1、下列判断中正确的是 ( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
2、正方形具有而矩形不一定有的性质是( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
3、矩形,菱形,正方形都具有的性质是 ( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补
D
B
C
4、在正方形ABCD中,∠ADB= ,∠DAC= , ∠BOC= .
5、在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
45°
90°
22.5°
45°
6、如图,分别延长等腰直角三角形OAB的两条直角边AO和BO,使AO=OC,BO=OD.求证:四边形ABCD是正方形.
证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形
∵等腰三角形OAB中,
AO⊥BO,AO=BO,
∴AO=BO=CO=DO ,AC⊥BD 即 AC=BD.
∴四边形ABCD是正方形.
7、如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形,
∴BC=DC,∠BCE =90° ,
∴∠DCF=180°-∠BCE=90°,
∴∠BCE=∠DCF.
又∵CE=CF,
∴△BCE≌△DCF.
∴BE=DF.
中考链接
【浙江】如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90 ° ,
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60 ° ,
∵∠CEF=45 ° ,
∴∠CFE=∠CEF=45 ° ,
∴∠AFD=∠AEB=180 ° 45 ° 60 ° =75 ° ,
∴△AEB △AFD(AAS) ,
∴AB=AD,∴矩形ABCD是正方形.
课堂小结
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
1.邻边相等的矩形是正方形
2.有一个角是直角的菱形是正方形
3.对角线相等且互相垂直平分的四边形是正方形
判定
19.3 正方形
华师大版数学八年级下册
第十九章 矩形,菱形,正方形
复习旧知
1.叙述平行四边形、矩形、菱形的定义和它们的特殊性质.
2.说一说平行四边形、矩形、菱形的内在联系.
情景导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
思考
你能从这个变化过程中给正方形下定义吗
有一个角是直角的菱形叫做正方形。
有一组邻边相等的矩形叫做正方形。
有一个角是直角一组邻边相等的平行四边形叫做正方形。
是直角
有一个角
边相等
有一组邻
边相等
有一组邻
是直角
有一个角
探究新知
由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.如图.
想一想
正方形是菱形吗?正方形具有哪些性质
正方形是特殊的菱形,它具有平行四边形、矩形、菱形的一切性质。
边:对边平行,四边都相等。
角:四个角都是直角
对角线:对角线相等且互相垂直平分
A
B
C
D
O
思考
正方形是轴对称图形吗 如果是,它有几条对称轴
正方形是轴对称图形,它有四条对称轴.即两条对角线,两组对边的中垂线.
对称:正方形既是轴对称图形,也是中心对称图形.
归纳总结
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
典例精析
A
C
D
B
O
例1、如图,已知正方形ABCD,求∠ABD、∠DAC、∠DOC的度数.
证明:∵四边形ABCD是正方形
∴AC⊥BD,∴∠DOC=90°
在△ABO与△CBO中
∴ △ABO≌△CBO ∴∠ABO=∠CBO
∴∠ABD= 同理可得∠DAC=45°
A
D
C
B
O
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
变式训练
探究新知
从图中可看出,
⑴在正方形中产生了哪些特殊图形?
⑵产生了哪些特殊角?
D
O
A
B
C
450
450
450
450
450
450
450
450
4个全等的小等腰直角三角形和4个全等的大等腰直角三角形.
900和450
正方形图形“庐山真面目”
思考
怎样判定一个矩形是正方形?怎样判定一个菱形是正方形?
怎样判定一个平行四边形是正方形?
探究新知
1 .定义法:
2.矩形法:
4.对角线法:
一邻边相等
一个直角
+
+
平行四边形
=
正方形
3.菱形法:
一邻边相等
+
矩形
=
正方形
一个直角
+
菱形
=
正方形
互相平分
+
互相垂直
相等
+
=
正方形
① 对角线相等的菱形是正方形 ( )
② 对角线互相垂直的矩形是正方形 ( )
③ 对角线互相垂直且相等的四边形是正方形 ( )
④ 四条边都相等的四边形是正方形 ( )
⑤ 四个角都相等的四边形是正方形 ( )
⑥ 四边相等,有一个角是直角的四边形是正方形.( )
判断对错
√
√
×
×
×
√
对应训练
典例精析
例、在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
典例精析
如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
证明:∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,∴四边形EDFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线 DE⊥AC,DG⊥AB,
∴ DE=DG. 同理得DG=DF,
∴ED=DF, ∴矩形EDFC是正方形.
变式训练
课堂练习
1、下列判断中正确的是 ( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
2、正方形具有而矩形不一定有的性质是( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
3、矩形,菱形,正方形都具有的性质是 ( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补
D
B
C
4、在正方形ABCD中,∠ADB= ,∠DAC= , ∠BOC= .
5、在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
45°
90°
22.5°
45°
6、如图,分别延长等腰直角三角形OAB的两条直角边AO和BO,使AO=OC,BO=OD.求证:四边形ABCD是正方形.
证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形
∵等腰三角形OAB中,
AO⊥BO,AO=BO,
∴AO=BO=CO=DO ,AC⊥BD 即 AC=BD.
∴四边形ABCD是正方形.
7、如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形,
∴BC=DC,∠BCE =90° ,
∴∠DCF=180°-∠BCE=90°,
∴∠BCE=∠DCF.
又∵CE=CF,
∴△BCE≌△DCF.
∴BE=DF.
中考链接
【浙江】如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90 ° ,
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60 ° ,
∵∠CEF=45 ° ,
∴∠CFE=∠CEF=45 ° ,
∴∠AFD=∠AEB=180 ° 45 ° 60 ° =75 ° ,
∴△AEB △AFD(AAS) ,
∴AB=AD,∴矩形ABCD是正方形.
课堂小结
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
1.邻边相等的矩形是正方形
2.有一个角是直角的菱形是正方形
3.对角线相等且互相垂直平分的四边形是正方形
判定
