1.1.1《空间向量及其运算》同步练习(含解析)
文档属性
| 名称 | 1.1.1《空间向量及其运算》同步练习(含解析) | 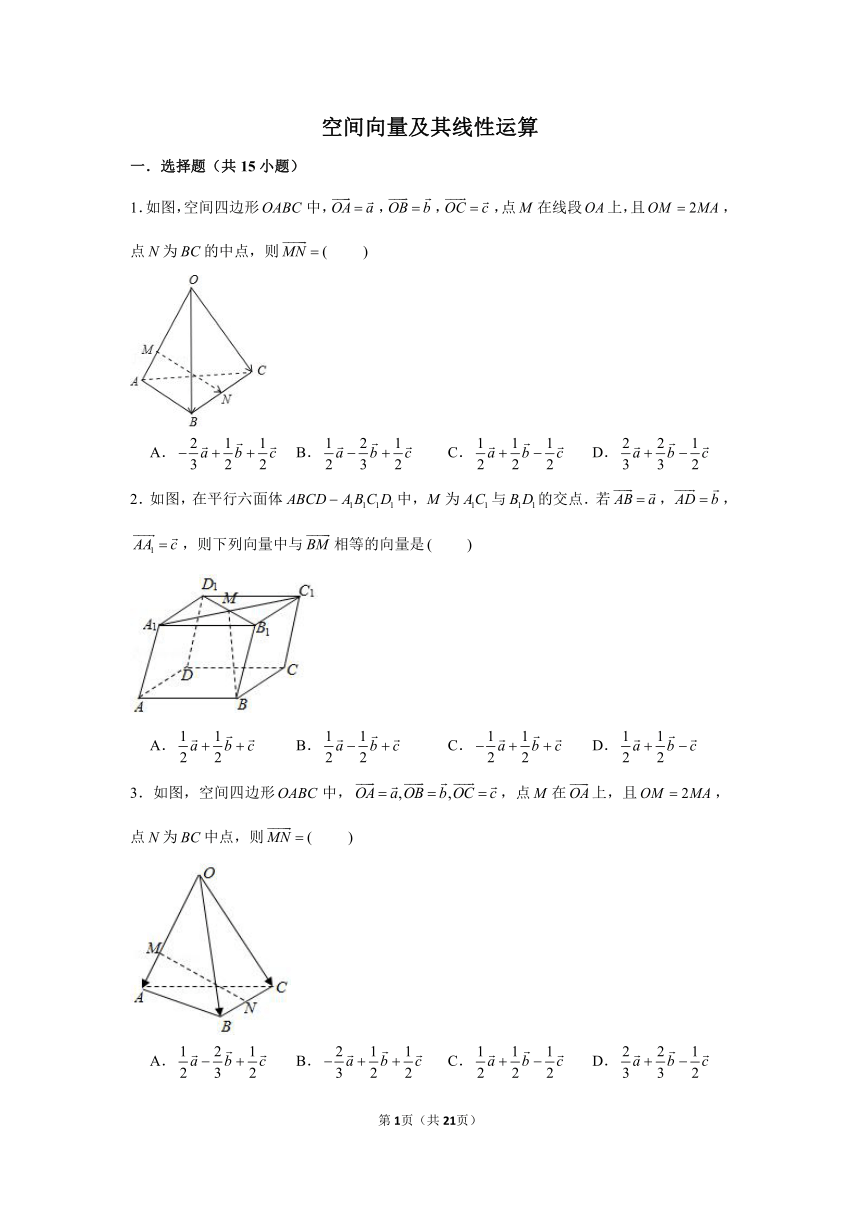 | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 10:19:38 | ||
图片预览





文档简介
空间向量及其线性运算
一.选择题(共15小题)
1.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
2.如图,在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是
A. B. C. D.
3.如图,空间四边形中,,点在上,且,点为中点,则
A. B. C. D.
4.如图,空间四边形中,,,,且,,则等于
A. B. C. D.
5.设是四面体,是的重心,是上一点,且,若,则,,为
A.,, B.,, C.,, D.,,
6.直三棱柱中,若,,,则
A. B. C. D.
7.已知三棱锥中,是的中点,则
A. B. C. D.
8.已知,1,,,,,是线段上一点,且,则点的坐标为
A.,, B.,, C.,, D.,,
9.已知正方体,点是的中点,点是的三等分点,且,则等于
A. B.
C. D.
10.已知点,,,向量,则点坐标是
A.,2, B.,2, C.,8, D.,,
11.在长方体中,
A. B. C. D.
12.如图所示,在平行六面体中,,,,是的中点,点是上的点,且.用表示向量的结果是
A. B. C. D.
13.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
14.平行六面体中,为与的交点,若,,,则下列式子中与相等的是
A. B. C. D.
15.若向量,,则
A. B. C.3 D.
二.多选题(共1小题)
16.已知向量,则与共线的单位向量
A. B.,1, C. D.,1,
三.填空题(共9小题)
17.在四面体中,,,,为的中点,为的中点,则 (用,,表示)
18.在三棱锥中,为的重心,设,,,则 (用,,表示).
19.已知空间向量,0,,,1,,则 .
20.如图,在空间四边形中,,,棱,,的中点分别为,,,若,则 .
21.设,是两个不共线的空间向量,若,,,且,,三点共线,则实数的值为 .
22.已知,,,,0,,,1,,若,则的坐标为 .
23.在空间四边形中,若,5,,,,,点,分别为线段,的中点,则 ,的坐标为 .
24.如图所示,在长方体中,为的中点.用,,表示,则 .
25.在正方体中,给出以下向量表达式:
①; ②; ③; ④.
其中能够化简为向量的是 .(把你认为正确的序号填上)
参考答案与试题解析
一.选择题(共15小题)
1.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
【分析】由题意,把,,三个向量看作是基向量,由图形根据向量的线性运算,将用三个基向量表示出来,即可得到答案,选出正确选项.
【解答】解:,
,
,
,
,,,
,
故选:.
【点评】本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题.
2.如图,在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是
A. B. C. D.
【分析】利用空间向量的加法的三角形法则,结合平行六面体的性质分析解答.
【解答】解:由题意,
;
故选:.
【点评】本题考查了空间向量的加法,满足三角形法则;比较基础.
3.如图,空间四边形中,,点在上,且,点为中点,则
A. B. C. D.
【分析】由题意,把,,三个向量看作是基向量,由图形根据向量的线性运算,将用三个基向量表示出来,即可得到答案,选出正确选项.
【解答】解:由题意
又,,
故选:.
【点评】本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题.
4.如图,空间四边形中,,,,且,,则等于
A. B. C. D.
【分析】根据空间向量的线性表示,用、和表示出即可.
【解答】解:由题意知,
.
故选:.
【点评】本题考查了空间向量的线性表示与应用问题,是基础题.
5.设是四面体,是的重心,是上一点,且,若,则,,为
A.,, B.,, C.,, D.,,
【分析】由题意推出,使得它用,,,来表示,从而求出,,的值,得到正确选项.
【解答】解:
,
而,,,.
故选:.
【点评】本题考查空间向量的加减法,考查待定系数法,是基础题.
6.直三棱柱中,若,,,则
A. B. C. D.
【分析】将向量分解成,然后将利用相等向量和向量的三角形法则将与化成用、、表示即可.
【解答】解:
故选:.
【点评】本题主要考查了空间向量的加减法,解题的关键是利用向量的三角形法则,属于基础题.
7.已知三棱锥中,是的中点,则
A. B. C. D.
【分析】取中点,连结,,推导出,由此能求出结果.
【解答】解:如图,取中点,连结,
三棱锥中,是的中点,
.
故选:.
【点评】本题考查空间向量及其线性运算,向量加法定理等基础知识,是基础题.
8.已知,1,,,,,是线段上一点,且,则点的坐标为
A.,, B.,, C.,, D.,,
【分析】利用向量的线性运算即可得出.
【解答】解:,,
.
故选:.
【点评】熟练掌握向量的线性运算是解题的关键.
9.已知正方体,点是的中点,点是的三等分点,且,则等于
A. B.
C. D.
【分析】如图所示,,,,,,,代入化简即可得出.
【解答】解:如图所示,
,,,,,,
.
故选:.
【点评】本题考查了向量共线定理、向量三角形法则与平行四边形法则,考查了推理能力与计算能力,属于中档题.
10.已知点,,,向量,则点坐标是
A.,2, B.,2, C.,8, D.,,
【分析】根据空间向量的线性运算与坐标表示,计算即可.
【解答】解:点,,,向量,
又,,,,
所以,,,
则点坐标是,,.
故选:.
【点评】本题考查了空间向量的线性运算与坐标表示问题,是基础题.
11.在长方体中,
A. B. C. D.
【分析】根据题意,画出图形,结合图形,利用空间向量的加法运算即可得出结论.
【解答】解:如图所示,
长方体中,
.
故选:.
【点评】本题考查了空间向量加法运算的几何意义问题,是基础题目.
12.如图所示,在平行六面体中,,,,是的中点,点是上的点,且.用表示向量的结果是
A. B. C. D.
【分析】连接,在△中,由向量加法的三角形法则知,由是的中点,
用表示出,由条件:点是上的点,且,得到,
再用表示向量即可.
【解答】解:连接,在△中,,
是的中点,,
点是上的点,且.
,
故选:.
【点评】本题考查了空间向量及其线性运算,熟练掌握平面向量的三角形加法法则,属于基础题.
13.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
【分析】由空间向量加法法则得到,由此能求出结果.
【解答】解:空间四边形中,,,,
点在线段上,且,点为的中点,
.
故选:.
【点评】本题考查向量的求法,考查空间向量加法法则等基础知识,考查运算求解能力,考查数形结合思想,是基础题.
14.平行六面体中,为与的交点,若,,,则下列式子中与相等的是
A. B. C. D.
【分析】推导出,由此能求出结果.
【解答】解:平行六面体中,为与的交点,
,,,
.
故选:.
【点评】本题考查命题真假的判断,考查空间向量的加法法则等基础知识,考查运算求解能力,考查数形结合思想,是基础题.
15.若向量,,则
A. B. C.3 D.
【分析】利用向量坐标运算法则能求出,由此能求出.
【解答】解:向量,,
,,,
.
故选:.
【点评】本题考查向量的模的求法,考查空间向量坐标运算法则等基础知识,考查运算求解能力,是基础题.
二.多选题(共1小题)
16.已知向量,则与共线的单位向量
A. B.,1, C. D.,1,
【分析】直接利用向量求出向量的模,进一步求出单位向量.
【解答】解:由于向量,
所以
根据单位向量的关系式,
可得或.
故选:.
【点评】本题考查向量的模和单位向量,属于基础题.
三.填空题(共9小题)
17.在四面体中,,,,为的中点,为的中点,则 (用,,表示)
【分析】利用为的中点,为的中点,,,化简可得结果.
【解答】解:在四面体中,,,,为的中点,为的中点,
,
故答案为:.
【点评】本题考查向量中点公式的应用,以及两个向量的加减法的法则和几何意义.
18.在三棱锥中,为的重心,设,,,则 (用,,表示).
【分析】利用三角形重心的性质定理、三角形法则、向量的线性运算即可得出.
【解答】解:如图,取的中点,
为的重心,
则在中,.
.
故答案为:.
【点评】本题考查了三角形重心的性质定理、三角形法则、向量的线性运算,考查了推理能力与计算能力,属于中档题.
19.已知空间向量,0,,,1,,则 ,, .
【分析】根据向量的坐标运算计算即可.
【解答】解:,0,,,1,,
,0,,1,
,,,
故答案为:,,.
【点评】本题考查了向量的坐标运算,熟练掌握运算公式是解题的关键,本题是一道基础题.
20.如图,在空间四边形中,,,棱,,的中点分别为,,,若,则 5 .
【分析】根据空间向量的线性运算,用、表示,从而求出的值.
【解答】解:空间四边形中,棱,,的中点分别为,,,
所以,;
所以
,
所以.
故答案为:5.
【点评】本题考查了空间向量的线性运算应用问题,也考查了运算求解能力,是基础题.
21.设,是两个不共线的空间向量,若,,,且,,三点共线,则实数的值为 .
【分析】先由求出,在根据,,三点共线,得到,从而得到,解出即可.
【解答】解:,,,
,
又,,三点共线,,
,,
故答案为:.
【点评】本题考查了三点共线和向量共线定理,考查了方程思想和计算能力,属基础题.
22.已知,,,,0,,,1,,若,则的坐标为 ,5, .
【分析】设出的坐标,利用向量相等,列出方程求解即可.
【解答】解:设,,,
,,,,0,,,1,,
,,,
,4,,
,
可得,,,
解得,,,
所以,5,.
故答案为:,5,.
【点评】本题考查空间向量的线性运算,点的坐标的求法,是基本知识的考查.
23.在空间四边形中,若,5,,,,,点,分别为线段,的中点,则 ,的坐标为 .
【分析】根据的坐标,求出的模即可,根据,求出的坐标即可.
【解答】解:,5,,,
点,分别为线段,的中点,设是坐标原点,
,,,
,,
,,,
故答案为:,,,.
【点评】本题考查了向量的运算,考查向量求模问题,是一道基础题.
24.如图所示,在长方体中,为的中点.用,,表示,则 .
【分析】利用三角形法则和平行四边形法则,即可得到.
【解答】解:.
故答案为:.
【点评】本题主要考查空间向量的运算,属于基础题.
25.在正方体中,给出以下向量表达式:
①; ②; ③; ④.
其中能够化简为向量的是 ①② .(把你认为正确的序号填上)
【分析】利用正方体的性质、向量的三角形法则即可得出.
【解答】解:如图所示
①;
②;
③;
④.
综上可得:只有①②能够化简为向量.
故答案为:①②.
【点评】本题考查了正方体的性质、向量的三角形法则,属于基础题.
声明:试题解析
第1页(共1页)
一.选择题(共15小题)
1.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
2.如图,在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是
A. B. C. D.
3.如图,空间四边形中,,点在上,且,点为中点,则
A. B. C. D.
4.如图,空间四边形中,,,,且,,则等于
A. B. C. D.
5.设是四面体,是的重心,是上一点,且,若,则,,为
A.,, B.,, C.,, D.,,
6.直三棱柱中,若,,,则
A. B. C. D.
7.已知三棱锥中,是的中点,则
A. B. C. D.
8.已知,1,,,,,是线段上一点,且,则点的坐标为
A.,, B.,, C.,, D.,,
9.已知正方体,点是的中点,点是的三等分点,且,则等于
A. B.
C. D.
10.已知点,,,向量,则点坐标是
A.,2, B.,2, C.,8, D.,,
11.在长方体中,
A. B. C. D.
12.如图所示,在平行六面体中,,,,是的中点,点是上的点,且.用表示向量的结果是
A. B. C. D.
13.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
14.平行六面体中,为与的交点,若,,,则下列式子中与相等的是
A. B. C. D.
15.若向量,,则
A. B. C.3 D.
二.多选题(共1小题)
16.已知向量,则与共线的单位向量
A. B.,1, C. D.,1,
三.填空题(共9小题)
17.在四面体中,,,,为的中点,为的中点,则 (用,,表示)
18.在三棱锥中,为的重心,设,,,则 (用,,表示).
19.已知空间向量,0,,,1,,则 .
20.如图,在空间四边形中,,,棱,,的中点分别为,,,若,则 .
21.设,是两个不共线的空间向量,若,,,且,,三点共线,则实数的值为 .
22.已知,,,,0,,,1,,若,则的坐标为 .
23.在空间四边形中,若,5,,,,,点,分别为线段,的中点,则 ,的坐标为 .
24.如图所示,在长方体中,为的中点.用,,表示,则 .
25.在正方体中,给出以下向量表达式:
①; ②; ③; ④.
其中能够化简为向量的是 .(把你认为正确的序号填上)
参考答案与试题解析
一.选择题(共15小题)
1.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
【分析】由题意,把,,三个向量看作是基向量,由图形根据向量的线性运算,将用三个基向量表示出来,即可得到答案,选出正确选项.
【解答】解:,
,
,
,
,,,
,
故选:.
【点评】本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题.
2.如图,在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是
A. B. C. D.
【分析】利用空间向量的加法的三角形法则,结合平行六面体的性质分析解答.
【解答】解:由题意,
;
故选:.
【点评】本题考查了空间向量的加法,满足三角形法则;比较基础.
3.如图,空间四边形中,,点在上,且,点为中点,则
A. B. C. D.
【分析】由题意,把,,三个向量看作是基向量,由图形根据向量的线性运算,将用三个基向量表示出来,即可得到答案,选出正确选项.
【解答】解:由题意
又,,
故选:.
【点评】本题考点是空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题.
4.如图,空间四边形中,,,,且,,则等于
A. B. C. D.
【分析】根据空间向量的线性表示,用、和表示出即可.
【解答】解:由题意知,
.
故选:.
【点评】本题考查了空间向量的线性表示与应用问题,是基础题.
5.设是四面体,是的重心,是上一点,且,若,则,,为
A.,, B.,, C.,, D.,,
【分析】由题意推出,使得它用,,,来表示,从而求出,,的值,得到正确选项.
【解答】解:
,
而,,,.
故选:.
【点评】本题考查空间向量的加减法,考查待定系数法,是基础题.
6.直三棱柱中,若,,,则
A. B. C. D.
【分析】将向量分解成,然后将利用相等向量和向量的三角形法则将与化成用、、表示即可.
【解答】解:
故选:.
【点评】本题主要考查了空间向量的加减法,解题的关键是利用向量的三角形法则,属于基础题.
7.已知三棱锥中,是的中点,则
A. B. C. D.
【分析】取中点,连结,,推导出,由此能求出结果.
【解答】解:如图,取中点,连结,
三棱锥中,是的中点,
.
故选:.
【点评】本题考查空间向量及其线性运算,向量加法定理等基础知识,是基础题.
8.已知,1,,,,,是线段上一点,且,则点的坐标为
A.,, B.,, C.,, D.,,
【分析】利用向量的线性运算即可得出.
【解答】解:,,
.
故选:.
【点评】熟练掌握向量的线性运算是解题的关键.
9.已知正方体,点是的中点,点是的三等分点,且,则等于
A. B.
C. D.
【分析】如图所示,,,,,,,代入化简即可得出.
【解答】解:如图所示,
,,,,,,
.
故选:.
【点评】本题考查了向量共线定理、向量三角形法则与平行四边形法则,考查了推理能力与计算能力,属于中档题.
10.已知点,,,向量,则点坐标是
A.,2, B.,2, C.,8, D.,,
【分析】根据空间向量的线性运算与坐标表示,计算即可.
【解答】解:点,,,向量,
又,,,,
所以,,,
则点坐标是,,.
故选:.
【点评】本题考查了空间向量的线性运算与坐标表示问题,是基础题.
11.在长方体中,
A. B. C. D.
【分析】根据题意,画出图形,结合图形,利用空间向量的加法运算即可得出结论.
【解答】解:如图所示,
长方体中,
.
故选:.
【点评】本题考查了空间向量加法运算的几何意义问题,是基础题目.
12.如图所示,在平行六面体中,,,,是的中点,点是上的点,且.用表示向量的结果是
A. B. C. D.
【分析】连接,在△中,由向量加法的三角形法则知,由是的中点,
用表示出,由条件:点是上的点,且,得到,
再用表示向量即可.
【解答】解:连接,在△中,,
是的中点,,
点是上的点,且.
,
故选:.
【点评】本题考查了空间向量及其线性运算,熟练掌握平面向量的三角形加法法则,属于基础题.
13.如图,空间四边形中,,,,点在线段上,且,点为的中点,则
A. B. C. D.
【分析】由空间向量加法法则得到,由此能求出结果.
【解答】解:空间四边形中,,,,
点在线段上,且,点为的中点,
.
故选:.
【点评】本题考查向量的求法,考查空间向量加法法则等基础知识,考查运算求解能力,考查数形结合思想,是基础题.
14.平行六面体中,为与的交点,若,,,则下列式子中与相等的是
A. B. C. D.
【分析】推导出,由此能求出结果.
【解答】解:平行六面体中,为与的交点,
,,,
.
故选:.
【点评】本题考查命题真假的判断,考查空间向量的加法法则等基础知识,考查运算求解能力,考查数形结合思想,是基础题.
15.若向量,,则
A. B. C.3 D.
【分析】利用向量坐标运算法则能求出,由此能求出.
【解答】解:向量,,
,,,
.
故选:.
【点评】本题考查向量的模的求法,考查空间向量坐标运算法则等基础知识,考查运算求解能力,是基础题.
二.多选题(共1小题)
16.已知向量,则与共线的单位向量
A. B.,1, C. D.,1,
【分析】直接利用向量求出向量的模,进一步求出单位向量.
【解答】解:由于向量,
所以
根据单位向量的关系式,
可得或.
故选:.
【点评】本题考查向量的模和单位向量,属于基础题.
三.填空题(共9小题)
17.在四面体中,,,,为的中点,为的中点,则 (用,,表示)
【分析】利用为的中点,为的中点,,,化简可得结果.
【解答】解:在四面体中,,,,为的中点,为的中点,
,
故答案为:.
【点评】本题考查向量中点公式的应用,以及两个向量的加减法的法则和几何意义.
18.在三棱锥中,为的重心,设,,,则 (用,,表示).
【分析】利用三角形重心的性质定理、三角形法则、向量的线性运算即可得出.
【解答】解:如图,取的中点,
为的重心,
则在中,.
.
故答案为:.
【点评】本题考查了三角形重心的性质定理、三角形法则、向量的线性运算,考查了推理能力与计算能力,属于中档题.
19.已知空间向量,0,,,1,,则 ,, .
【分析】根据向量的坐标运算计算即可.
【解答】解:,0,,,1,,
,0,,1,
,,,
故答案为:,,.
【点评】本题考查了向量的坐标运算,熟练掌握运算公式是解题的关键,本题是一道基础题.
20.如图,在空间四边形中,,,棱,,的中点分别为,,,若,则 5 .
【分析】根据空间向量的线性运算,用、表示,从而求出的值.
【解答】解:空间四边形中,棱,,的中点分别为,,,
所以,;
所以
,
所以.
故答案为:5.
【点评】本题考查了空间向量的线性运算应用问题,也考查了运算求解能力,是基础题.
21.设,是两个不共线的空间向量,若,,,且,,三点共线,则实数的值为 .
【分析】先由求出,在根据,,三点共线,得到,从而得到,解出即可.
【解答】解:,,,
,
又,,三点共线,,
,,
故答案为:.
【点评】本题考查了三点共线和向量共线定理,考查了方程思想和计算能力,属基础题.
22.已知,,,,0,,,1,,若,则的坐标为 ,5, .
【分析】设出的坐标,利用向量相等,列出方程求解即可.
【解答】解:设,,,
,,,,0,,,1,,
,,,
,4,,
,
可得,,,
解得,,,
所以,5,.
故答案为:,5,.
【点评】本题考查空间向量的线性运算,点的坐标的求法,是基本知识的考查.
23.在空间四边形中,若,5,,,,,点,分别为线段,的中点,则 ,的坐标为 .
【分析】根据的坐标,求出的模即可,根据,求出的坐标即可.
【解答】解:,5,,,
点,分别为线段,的中点,设是坐标原点,
,,,
,,
,,,
故答案为:,,,.
【点评】本题考查了向量的运算,考查向量求模问题,是一道基础题.
24.如图所示,在长方体中,为的中点.用,,表示,则 .
【分析】利用三角形法则和平行四边形法则,即可得到.
【解答】解:.
故答案为:.
【点评】本题主要考查空间向量的运算,属于基础题.
25.在正方体中,给出以下向量表达式:
①; ②; ③; ④.
其中能够化简为向量的是 ①② .(把你认为正确的序号填上)
【分析】利用正方体的性质、向量的三角形法则即可得出.
【解答】解:如图所示
①;
②;
③;
④.
综上可得:只有①②能够化简为向量.
故答案为:①②.
【点评】本题考查了正方体的性质、向量的三角形法则,属于基础题.
声明:试题解析
第1页(共1页)
