4.4探索三角形相似的条件 同步训练(含答案)2023-2024学年北师大九年级数学上册
文档属性
| 名称 | 4.4探索三角形相似的条件 同步训练(含答案)2023-2024学年北师大九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 553.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 18:10:15 | ||
图片预览


文档简介
2023-2024学年九年级上册4.4探索三角形相似的条件 同步训练
一、选择题
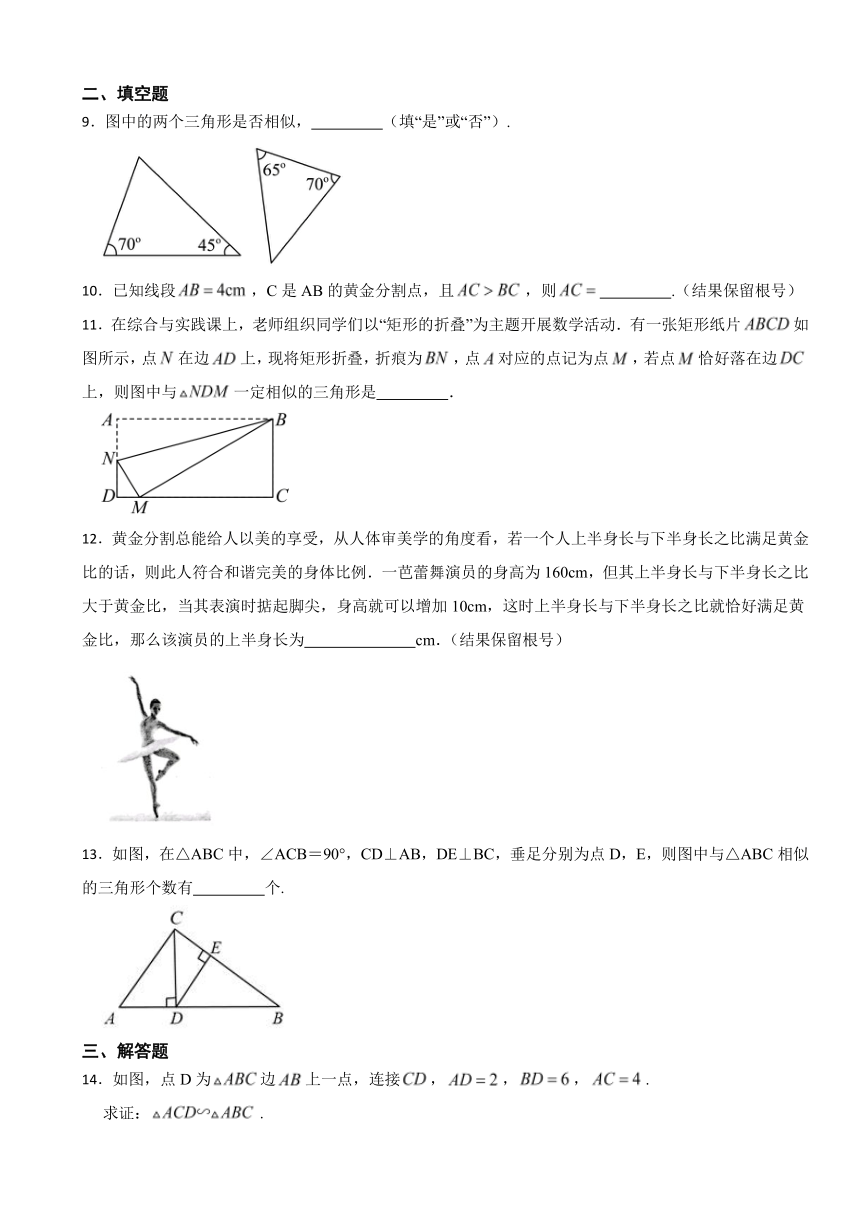
1.如图,能使成立的条件是( )
A. B.
C. D.
2.神奇的自然界处处隐含着数学美!生物学家在向日葵圆盘中发现:向日葵籽粒成螺线状排列,螺线的发散角是.我们知道圆盘一周为,,.这体现了( )
A.轴对称 B.旋转 C.平移 D.黄金分割
3.如图,在由小正方形组成的方格纸中,和的顶点均在格点上,要使,则点所在的格点为( )
A. B. C. D.
4.已知点C是线段AB的黄金分割点(AC>BC),若AB=4,则AC的长为( )
A.(6﹣2) B.(2﹣2)
C.(﹣1) D.(3﹣)
5.下列判断中,正确的是( )
A.各有一个角是的两个等腰三角形相似
B.邻边之比为2:1的两个等腰三角形相似
C.各有一个角是的两个等腰三角形相似
D.邻边之比为2:3的两个等腰三角形相似
6.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A. B.
C. D.
7.如图,在中,点D,E分别是,上的点,与交于点F,下列条件中不能使和相似的是( )
A. B.
C. D.
8.一个钢筋三脚架三边长分别为,现在要做一个和它相似的钢筋三脚架,而只有长为和的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A.一种 B.两种
C.三种 D.四种或四种以上
二、填空题
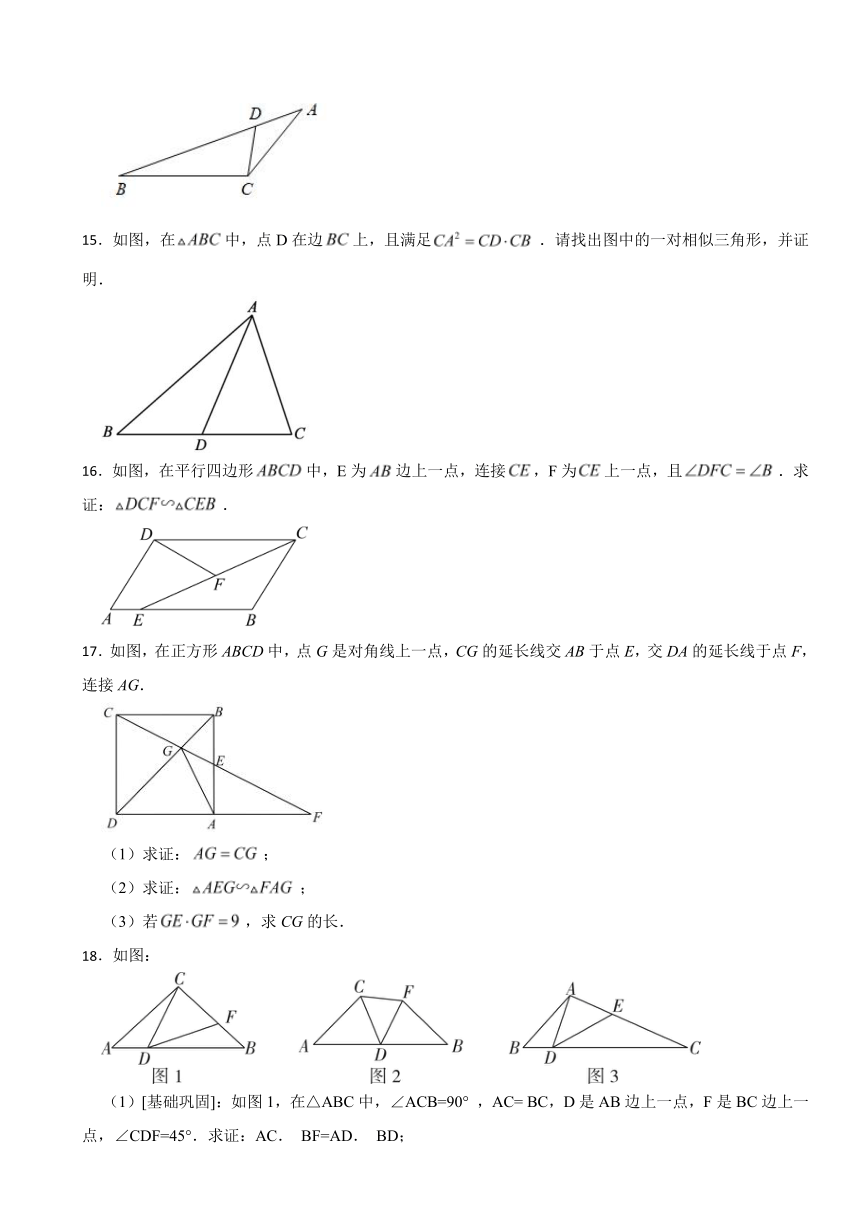
9.图中的两个三角形是否相似, (填“是”或“否”).
10.已知线段,C是AB的黄金分割点,且,则 .(结果保留根号)
11.在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为,点对应的点记为点,若点恰好落在边上,则图中与一定相似的三角形是 .
12.黄金分割总能给人以美的享受,从人体审美学的角度看,若一个人上半身长与下半身长之比满足黄金比的话,则此人符合和谐完美的身体比例.一芭蕾舞演员的身高为160cm,但其上半身长与下半身长之比大于黄金比,当其表演时掂起脚尖,身高就可以增加10cm,这时上半身长与下半身长之比就恰好满足黄金比,那么该演员的上半身长为 cm.(结果保留根号)
13.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为点D,E,则图中与△ABC相似的三角形个数有 个.
三、解答题
14.如图,点D为边上一点,连接,,,.
求证:.
15.如图,在中,点D在边上,且满足.请找出图中的一对相似三角形,并证明.
16.如图,在平行四边形中,E为边上一点,连接,F为上一点,且.求证:.
17.如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
(1)求证:;
(2)求证:;
(3)若,求CG的长.
18.如图:
(1)[基础巩固]:如图1,在△ABC中,∠ACB=90° ,AC= BC,D是AB边上一点,F是BC边上一点,∠CDF=45°.求证:AC. BF=AD. BD;
(2)[尝试应用]如图2,在四边形ABFC中,点D是AB边的中点,∠A=∠B=∠CDF=45°,若AC=9,BF=8,求线段CF的长.
(3)[拓展提高]如图3,在△ABC中,AB=4,∠B=45°.以A为直角顶点作等腰直角三角形ADE,点D在BC上,点E在AC上.若CE=2,求CD的长.
答案解析部分
1. C
2.D
3.B
4.B
5.B
6.D
7.C
8.B
9.是
10.
11.
12.
13.4
14.证明:∵,,
∴,
∴,,即,
又∵,
∴
15.解:;
∵,
∴,
∵,
∴.
16.证明:∵四边形是平行四边形,
∴
∴.
∵
∴;
17.(1)证明:∵BD是正方形ABCD的对角线,
∴,又,
在和中,,∴(SAS),∴;
(2)证明:∵四边形ABCD是正方形,∴,∴,
由(1)可知,
∴,∴,即,∴,
又,∴;
(3)解:由(2)得,∴,即,
∴或(舍去),根据(1)中的结论得,∴.
18.(1)证明:∵∠ABC=90°,AC= BC,
∴∠A=∠B=45,
∵∠A+∠ACD=∠CDF+∠BDF,∠A=∠CDF=45°,
∴∠ACD=∠BDF,
∴△ACD∽△BDF,
∴
∴AC·BF =AD·BD.
(2)解:如图2中,延长AC交BF的延长线于点T.
∵∠A=∠CDF=∠B=45°,
∴∠T=90°,TA=TB,
∵∠CDB=∠A+∠ACD=∠CDF+∠BDF,
∴∠ACD=∠BDF,
故△ACD∽△BDF,
∴
∵AD=DB,
∴
∴AD=6,
∴AB=2AD=12,
∴TA=TB=12,
∴CT=12-9=3,TF=12-8=4,
∴CF==5
(3)解:如图,过点E作EF与CD交于点F,使∠EFD=45°,
∵∠B=∠ADE=45°,
∴∠BAD=∠EDF ,
∴△ABD∽△DFE,
∴
∵DE=AD,AB=4,
∴DF=AB=8,
∵∠EFD=45°,∠ADE=45°,
∴∠EFC=∠DEC= 135°,
∴△EFC∽△DEC ,
∴
∴EC=2,
∴EC2= FC·CD= FC×(8+FC),
∴20= FC×(8+ FC),
∴FC=2,
∴CD=10.
一、选择题
1.如图,能使成立的条件是( )
A. B.
C. D.
2.神奇的自然界处处隐含着数学美!生物学家在向日葵圆盘中发现:向日葵籽粒成螺线状排列,螺线的发散角是.我们知道圆盘一周为,,.这体现了( )
A.轴对称 B.旋转 C.平移 D.黄金分割
3.如图,在由小正方形组成的方格纸中,和的顶点均在格点上,要使,则点所在的格点为( )
A. B. C. D.
4.已知点C是线段AB的黄金分割点(AC>BC),若AB=4,则AC的长为( )
A.(6﹣2) B.(2﹣2)
C.(﹣1) D.(3﹣)
5.下列判断中,正确的是( )
A.各有一个角是的两个等腰三角形相似
B.邻边之比为2:1的两个等腰三角形相似
C.各有一个角是的两个等腰三角形相似
D.邻边之比为2:3的两个等腰三角形相似
6.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A. B.
C. D.
7.如图,在中,点D,E分别是,上的点,与交于点F,下列条件中不能使和相似的是( )
A. B.
C. D.
8.一个钢筋三脚架三边长分别为,现在要做一个和它相似的钢筋三脚架,而只有长为和的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A.一种 B.两种
C.三种 D.四种或四种以上
二、填空题
9.图中的两个三角形是否相似, (填“是”或“否”).
10.已知线段,C是AB的黄金分割点,且,则 .(结果保留根号)
11.在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为,点对应的点记为点,若点恰好落在边上,则图中与一定相似的三角形是 .
12.黄金分割总能给人以美的享受,从人体审美学的角度看,若一个人上半身长与下半身长之比满足黄金比的话,则此人符合和谐完美的身体比例.一芭蕾舞演员的身高为160cm,但其上半身长与下半身长之比大于黄金比,当其表演时掂起脚尖,身高就可以增加10cm,这时上半身长与下半身长之比就恰好满足黄金比,那么该演员的上半身长为 cm.(结果保留根号)
13.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为点D,E,则图中与△ABC相似的三角形个数有 个.
三、解答题
14.如图,点D为边上一点,连接,,,.
求证:.
15.如图,在中,点D在边上,且满足.请找出图中的一对相似三角形,并证明.
16.如图,在平行四边形中,E为边上一点,连接,F为上一点,且.求证:.
17.如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
(1)求证:;
(2)求证:;
(3)若,求CG的长.
18.如图:
(1)[基础巩固]:如图1,在△ABC中,∠ACB=90° ,AC= BC,D是AB边上一点,F是BC边上一点,∠CDF=45°.求证:AC. BF=AD. BD;
(2)[尝试应用]如图2,在四边形ABFC中,点D是AB边的中点,∠A=∠B=∠CDF=45°,若AC=9,BF=8,求线段CF的长.
(3)[拓展提高]如图3,在△ABC中,AB=4,∠B=45°.以A为直角顶点作等腰直角三角形ADE,点D在BC上,点E在AC上.若CE=2,求CD的长.
答案解析部分
1. C
2.D
3.B
4.B
5.B
6.D
7.C
8.B
9.是
10.
11.
12.
13.4
14.证明:∵,,
∴,
∴,,即,
又∵,
∴
15.解:;
∵,
∴,
∵,
∴.
16.证明:∵四边形是平行四边形,
∴
∴.
∵
∴;
17.(1)证明:∵BD是正方形ABCD的对角线,
∴,又,
在和中,,∴(SAS),∴;
(2)证明:∵四边形ABCD是正方形,∴,∴,
由(1)可知,
∴,∴,即,∴,
又,∴;
(3)解:由(2)得,∴,即,
∴或(舍去),根据(1)中的结论得,∴.
18.(1)证明:∵∠ABC=90°,AC= BC,
∴∠A=∠B=45,
∵∠A+∠ACD=∠CDF+∠BDF,∠A=∠CDF=45°,
∴∠ACD=∠BDF,
∴△ACD∽△BDF,
∴
∴AC·BF =AD·BD.
(2)解:如图2中,延长AC交BF的延长线于点T.
∵∠A=∠CDF=∠B=45°,
∴∠T=90°,TA=TB,
∵∠CDB=∠A+∠ACD=∠CDF+∠BDF,
∴∠ACD=∠BDF,
故△ACD∽△BDF,
∴
∵AD=DB,
∴
∴AD=6,
∴AB=2AD=12,
∴TA=TB=12,
∴CT=12-9=3,TF=12-8=4,
∴CF==5
(3)解:如图,过点E作EF与CD交于点F,使∠EFD=45°,
∵∠B=∠ADE=45°,
∴∠BAD=∠EDF ,
∴△ABD∽△DFE,
∴
∵DE=AD,AB=4,
∴DF=AB=8,
∵∠EFD=45°,∠ADE=45°,
∴∠EFC=∠DEC= 135°,
∴△EFC∽△DEC ,
∴
∴EC=2,
∴EC2= FC·CD= FC×(8+FC),
∴20= FC×(8+ FC),
∴FC=2,
∴CD=10.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
