《第21—22章》综合练习题 (含解析)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 《第21—22章》综合练习题 (含解析)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 299.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览




文档简介
2023-2024学年人教版九年级数学上册《第21—22章》综合练习题(附答案)
一、选择题(共30分)
1.下列方程是一元二次方程的是( )
A.x2=x B.ax2+bx+c=0 C.xy=1 D.
2.将方程2x(1﹣2x)=5x(2﹣x)﹣3化为一般形式后为( )
A.x2﹣8x﹣3=0 B.9x2+12x﹣3=0
C.x2﹣8x+3=0 D.9x2﹣12x+3=0
3.抛物线y=2(x﹣3)2+2的顶点坐标是( )
A.(﹣3,2) B.(3,2) C.(﹣3,﹣2) D.(3,﹣2)
4.一元二次方程x(x﹣2)=2﹣x的根是( )
A.x=﹣1 B.x=2 C.x1=1,x2=2 D.x1=﹣1,x2=2
5.已知等腰三角形的两边长分别是方程x2﹣7x+12=0的两根,则该等腰三角形的底边长为( )
A.3 B.4 C.7 D.3或4
6.若实数a,b(a≠b)分别满足方程a2﹣7a+2=0,b2﹣7b+2=0,则的值为( )
A. B. C.或2 D.或2
7.如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B.
C. D.
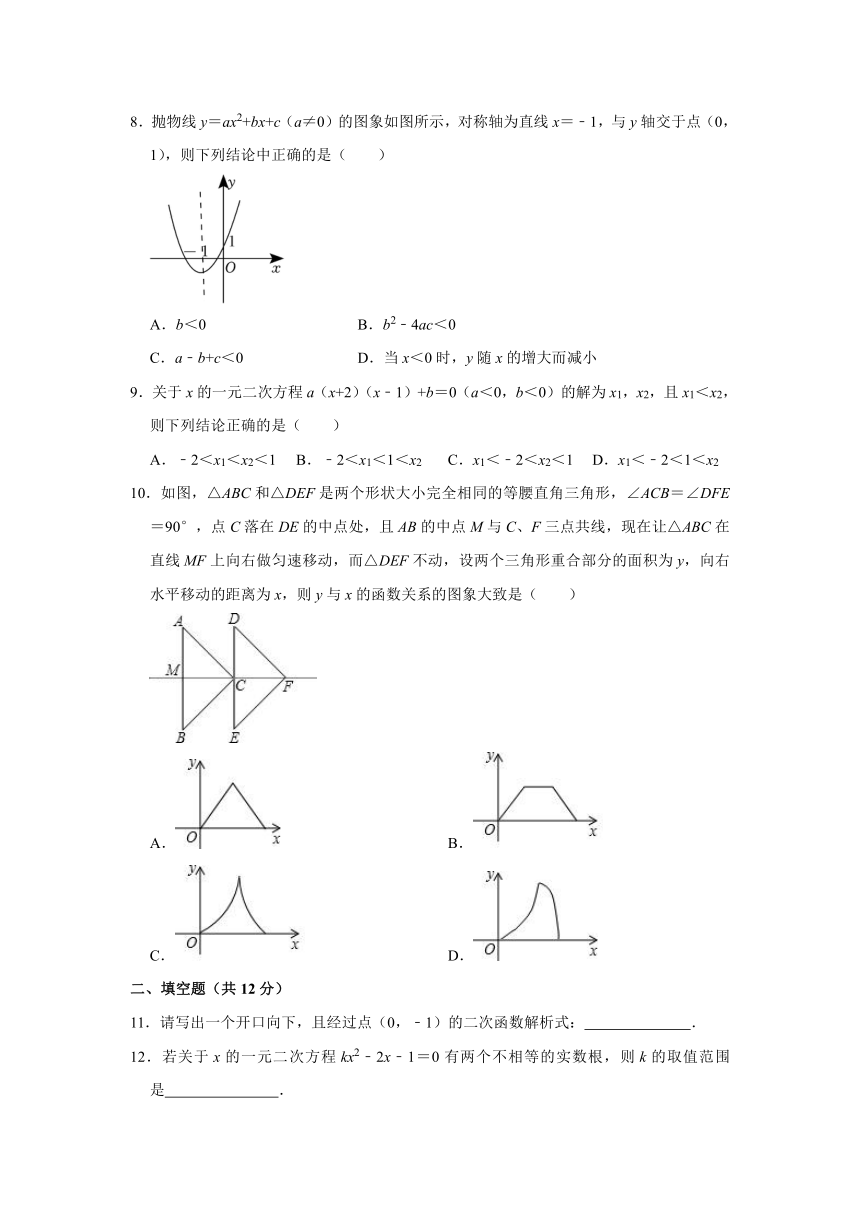
8.抛物线y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,与y轴交于点(0,1),则下列结论中正确的是( )
A.b<0 B.b2﹣4ac<0
C.a﹣b+c<0 D.当x<0时,y随x的增大而减小
9.关于x的一元二次方程a(x+2)(x﹣1)+b=0(a<0,b<0)的解为x1,x2,且x1<x2,则下列结论正确的是( )
A.﹣2<x1<x2<1 B.﹣2<x1<1<x2 C.x1<﹣2<x2<1 D.x1<﹣2<1<x2
10.如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠ACB=∠DFE=90°,点C落在DE的中点处,且AB的中点M与C、F三点共线,现在让△ABC在直线MF上向右做匀速移动,而△DEF不动,设两个三角形重合部分的面积为y,向右水平移动的距离为x,则y与x的函数关系的图象大致是( )
A. B.
C. D.
二、填空题(共12分)
11.请写出一个开口向下,且经过点(0,﹣1)的二次函数解析式: .
12.若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是 .
13.若α、β是方程x2+3x﹣1=0的两个实数根,则α2+2α﹣β= .
14.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表.
x ﹣1 0 1 3
y ﹣1 3 5 3
解答下列问题:
(1)方程ax2+(b﹣1)x+c=0的根是 ;
(2)当ax2+bx+c>﹣1时,x的取值范围是 .
三、解答题(满分78分)
15.解方程:2x2﹣x﹣1=0.
16.已知关于x的一元二次方程x2﹣6x+m2﹣3m﹣5=0的一个根是﹣1,求m的值及方程的另一个根.
17.二次函数y=x2+bx+c的图象过点A(﹣2,5),且当x=2时,y=﹣3,求这个二次函数的解析式,并判断点B(0,3)是否在这个函数的图象上.
18.已知函数和y2=mx+n的图象交于点(﹣2,﹣5)和点(1,4),并且的图象与y轴交于点(0,3).
(1)求函数y1和y2的解析式;
(2)直接写出x为何值时,
①y1>y2;
②y1=y2;
③y1<y2.
19.如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
20.一元二次方程mx2﹣2mx+m﹣2=0.
(1)若方程有两实数根,求m的范围.
(2)设方程两实根为x1,x2,且|x1﹣x2|=1,求m.
21.如图,二次函数y=ax2+bx+c的图象与x轴相交于点A、B,与y轴相交于点C.过点C作CD⊥y轴,交该图象于点D.若B(8,0)、D(6,4).
(1)求该抛物线的对称轴;
(2)求△ABC的面积.
22.如图,一农户原来种植的花生,每公顷产量为3000kg,出油率为50%(即每100kg花生可加工出花生油50kg).现在种植新品种花生后,每公顷收获的花生可加工出花生油1980kg,已知花生出油率的增长率是产量增长率的,求新品种花生产量的增长率.
23.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.解答下列问题:(注意:取,)
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)求足球第二次飞出到落地时,该抛物线的表达式.
参考答案
一、选择题(共30分)
1.解:A.方程x2=x是一元二次方程,符合题意;
B.当a=0时,该方程不是一元二次方程,故该选项不符合题意;
C.xy=1是二元二次方程,不符合题意;
D.方x+=1是分式方程,不符合题意.
故选:A.
2.解:由原方程,得
2x﹣4x2=10x﹣5x2﹣3,
则x2﹣8x+3=0.
故选:C.
3.解:抛物线y=2(x﹣3)2+2的顶点坐标是(3,2),
故选:B.
4.解:x(x﹣2)+(x﹣2)=0,
(x﹣2)(x+1)=0,
x﹣2=0或x+1=0,
所以x1=2,x2=﹣1.
故选:D.
5.解:∵x2﹣7x+12=0,
∴(x﹣3)(x﹣4)=0,
∴x﹣3=0或x﹣4=0,
解得:x1=3,x2=4,
∴等腰三角形的两边长分别3或4;
∴该等腰三角形的底边长为3或4;
故选:D.
6.解:由实数a,b满足条件a2﹣7a+2=0,b2﹣7b+2=0,
∴可把a,b看成是方程x2﹣7x+2=0的两个根,
∴a+b=7,ab=2,
∴====.
故选:A.
7.解:当k>0时,函数y=kx﹣2的图象经过一、三、四象限;函数y=kx2的开口向上,对称轴在y轴上;
当k<0时,函数y=kx﹣2的图象经过二、三、四象限;函数y=kx2的开口向下,对称轴在y轴上,故C正确.
故选:C.
8.解:选项A,∵抛物线开口向上,
∴a>0.
∵抛物线的对称轴为x=﹣1,
∴﹣=﹣1,即b=2a.
∴b>0.故选项A错误;
选项B,∵抛物线y=ax2+bx+c与x轴有两个公共点,
∴一元二次方程ax2+bx+c=0有两个不等的实数根.
∴b2﹣4ac>0.故选项B错误;
选项C,由题图可知,当x=﹣1时,抛物线有最低点,且在x轴下方,
∴二次函数有最小值,且y最小<0.
∴当x=﹣1时,二次函数的值y=a﹣b+c<0.故选项C正确;
选项D,由图可知,当x<﹣1时,y随x的增大而减小,当﹣1<x<0时,y随x的增大而增大.
∴当x<0时,y随x增大而减小是错误的,故选项D错误.
故选:C.
9.解:关于x的一元二次方程a(x+2)(x﹣1)+b=0(a<0,b>0)的解就是函数y=a(x+2)(x﹣1)与y=﹣b的交点的横坐标,
∵a<0,
∴抛物线开口向下,
∵b<0,
∴y=﹣b在x轴下方,
∵x1<x2,
如图所示:
∴x1<﹣2<1<x2,
故选:D.
10.解:本题的运动过程应分两部分,从开始到两三角形重合,另一部分是从重合到分离;
在第一部分,三角形ABC在直线MF上向右做匀速运动,则重合部分面积的增加速度不断变快;而另一部分面积的减小速度越来越小.
故选:C.
二、填空题(共12分)
11.解:∵开口向下且过点(0,﹣1)的抛物线解析式,
∴可以设顶点坐标为(0,﹣1),
故解析式为:y=﹣x2﹣1(答案不唯一).
故答案为:y=﹣x2﹣1(答案不唯一).
12.解:∵关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,
∴Δ=b2﹣4ac=(﹣2)2﹣4×k×(﹣1)=4+4k>0,
∴k>﹣1,
∵x的一元二次方程kx2﹣2x﹣1=0
∴k≠0,
∴k的取值范围是:k>﹣1且k≠0.
故答案为:k>﹣1且k≠0.
13.解:∵α方程x2+3x﹣1=0的实数根,
∴α2+3α﹣1=0,
∴α2=﹣3α+1,
∴α2+2α﹣β=﹣3α+1+2α﹣β
=﹣(α+β)+1,
∵α、β是方程x2+3x﹣1=0的两个实数根,
∴α+β=﹣3,
∴α2+2α﹣β=3+1=4.
故答案为4.
14.解:(1)由ax2+(b﹣1)x+c=0,得ax2+bx+c=x,
可知二次函数y=ax2+bx+c与一次函数y=x的交点为(﹣1,﹣1)和(3,3),
所以方程ax2+bx+c=x的根是x1=﹣1,x2=3;
(2)根据表格可知抛物线的对称轴是,当时,函数值y随着x的增大而增大,
∴抛物线开口向下.
,
解得x=4,
可知当x=﹣1和x=4时,y=﹣1.
∴当﹣1<x<4时,ax2+bx+c>﹣1.
故答案为:﹣1,3;﹣1<x<4.
三、解答题(满分78分)
15.解方程:2x2﹣x﹣1=0,
(x﹣1)(2x+1)=0,
x﹣1=0,2x+1=0,
∴.
16.解:设方程的另一根为x2.
∵关于x的一元二次方程x2﹣6x+m2﹣3m﹣5=0的一个根是﹣1,
∴x=﹣1满足关于x的一元二次方程x2﹣6x+m2﹣3m﹣5=0,
∴(﹣1)2﹣6×(﹣1)+m2﹣3m﹣5=0,即m2﹣3m+2=0,
∴(m﹣1)(m﹣2)=0,
解得,m=1或m=2;
又由韦达定理知﹣1+x2=6,
解得,x2=7.即方程的另一根是7.
17.解:把A(﹣2,5),点(2,﹣3)代入y=x2+bx+c得,解得,
所以二次函数的解析式为y=x2﹣2x﹣3;
当x=0时,y=0﹣0﹣3=﹣3,
所以点B(0,3)不在这个函数的图象上.
18.解:(1)把点(﹣2,﹣5)、点(1,4)、点(0,3)代入得,
,
解得,
∴;
把点(﹣2,﹣5)和点(1,4)代入y2=mx+n得,
解得,
∴y2=3x+1.
(2)如图,在同一坐标系中画出和y2=3x+1的图象,
由图象可得①当﹣2<x<1时,y1>y2;②当x=﹣2或x=1时,y1=y2;③当x>1或x<﹣2时,y1<y2.
19.解:设宽为x m,则长为(16﹣2x)m.
由题意,得 x (16﹣2x)=30,
解得 x1=3,x2=5.
当x=3时,16﹣2×3=10,
当x=5时,16﹣2×5=6.
答:围成矩形的长为10 m、宽为3 m,或长为6 m、宽为5m.
20.解:(1)∵关于x的一元二次方程mx2﹣2mx+m﹣2=0有两个实数根,
∴m≠0且△≥0,即(﹣2m)2﹣4 m (m﹣2)≥0,
解得m≠0且m≥0,
∴m的取值范围为m>0.
(2)∵方程两实根为x1,x2,
∴x1+x2=2,x1 x2=,
∵|x1﹣x2|=1,
∴(x1﹣x2)2=1,
∴(x1+x2)2﹣4x1x2=1,
∴22﹣4×=1,
解得:m=8;
经检验m=8是原方程的解.
21.解:(1)∵CD⊥y轴,
∴C,D两点关于抛物线对称轴对称D(6,4),
∴C(0,4),
∴此抛物线的对称轴为直线:,即x=3
(2)连接AC,
∵A,B关于对称轴对称,B(8,0),
抛物线的对称轴为直线:x=3,
∴A(﹣2,0),
∴AB=8﹣(﹣2)=10,
∴△ABC的面积=.
22.解:设新品种花生产量的增长率为x,则新品种花生出油率的增长率为x,
根据题意得:3000(1+x)×50%(1+x)=1980,
整理得:x2+3x﹣0.64=0,
解得:x1=0.2=20%,x2=﹣3.2(不符合题意,舍去).
答:新品种花生产量的增长率为20%.
23.解:(1)由题意知,A(0,1),B(6,0),顶点坐标M(6,4),
设足球开始飞出到第一次落地时,抛物线的表达式为y=a(x﹣6)2+4,
将A(0,1)代入得,1=a(0﹣6)2+4,
解得,
∴,
∴足球开始飞出到第一次落地时,抛物线的表达式为;
(2)当y=0时,,
解得:,(不合题意,舍去),
∴C(13,0),
由题意,设第二次落地的抛物线的顶点坐标为(k,2),设第二次落地的抛物线为,
当x=13时,,
解得,(不合题意,舍去),
∴,
∴足球第二次飞出到落地时,抛物线的表达式为.
一、选择题(共30分)
1.下列方程是一元二次方程的是( )
A.x2=x B.ax2+bx+c=0 C.xy=1 D.
2.将方程2x(1﹣2x)=5x(2﹣x)﹣3化为一般形式后为( )
A.x2﹣8x﹣3=0 B.9x2+12x﹣3=0
C.x2﹣8x+3=0 D.9x2﹣12x+3=0
3.抛物线y=2(x﹣3)2+2的顶点坐标是( )
A.(﹣3,2) B.(3,2) C.(﹣3,﹣2) D.(3,﹣2)
4.一元二次方程x(x﹣2)=2﹣x的根是( )
A.x=﹣1 B.x=2 C.x1=1,x2=2 D.x1=﹣1,x2=2
5.已知等腰三角形的两边长分别是方程x2﹣7x+12=0的两根,则该等腰三角形的底边长为( )
A.3 B.4 C.7 D.3或4
6.若实数a,b(a≠b)分别满足方程a2﹣7a+2=0,b2﹣7b+2=0,则的值为( )
A. B. C.或2 D.或2
7.如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B.
C. D.
8.抛物线y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,与y轴交于点(0,1),则下列结论中正确的是( )
A.b<0 B.b2﹣4ac<0
C.a﹣b+c<0 D.当x<0时,y随x的增大而减小
9.关于x的一元二次方程a(x+2)(x﹣1)+b=0(a<0,b<0)的解为x1,x2,且x1<x2,则下列结论正确的是( )
A.﹣2<x1<x2<1 B.﹣2<x1<1<x2 C.x1<﹣2<x2<1 D.x1<﹣2<1<x2
10.如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠ACB=∠DFE=90°,点C落在DE的中点处,且AB的中点M与C、F三点共线,现在让△ABC在直线MF上向右做匀速移动,而△DEF不动,设两个三角形重合部分的面积为y,向右水平移动的距离为x,则y与x的函数关系的图象大致是( )
A. B.
C. D.
二、填空题(共12分)
11.请写出一个开口向下,且经过点(0,﹣1)的二次函数解析式: .
12.若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是 .
13.若α、β是方程x2+3x﹣1=0的两个实数根,则α2+2α﹣β= .
14.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表.
x ﹣1 0 1 3
y ﹣1 3 5 3
解答下列问题:
(1)方程ax2+(b﹣1)x+c=0的根是 ;
(2)当ax2+bx+c>﹣1时,x的取值范围是 .
三、解答题(满分78分)
15.解方程:2x2﹣x﹣1=0.
16.已知关于x的一元二次方程x2﹣6x+m2﹣3m﹣5=0的一个根是﹣1,求m的值及方程的另一个根.
17.二次函数y=x2+bx+c的图象过点A(﹣2,5),且当x=2时,y=﹣3,求这个二次函数的解析式,并判断点B(0,3)是否在这个函数的图象上.
18.已知函数和y2=mx+n的图象交于点(﹣2,﹣5)和点(1,4),并且的图象与y轴交于点(0,3).
(1)求函数y1和y2的解析式;
(2)直接写出x为何值时,
①y1>y2;
②y1=y2;
③y1<y2.
19.如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
20.一元二次方程mx2﹣2mx+m﹣2=0.
(1)若方程有两实数根,求m的范围.
(2)设方程两实根为x1,x2,且|x1﹣x2|=1,求m.
21.如图,二次函数y=ax2+bx+c的图象与x轴相交于点A、B,与y轴相交于点C.过点C作CD⊥y轴,交该图象于点D.若B(8,0)、D(6,4).
(1)求该抛物线的对称轴;
(2)求△ABC的面积.
22.如图,一农户原来种植的花生,每公顷产量为3000kg,出油率为50%(即每100kg花生可加工出花生油50kg).现在种植新品种花生后,每公顷收获的花生可加工出花生油1980kg,已知花生出油率的增长率是产量增长率的,求新品种花生产量的增长率.
23.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.解答下列问题:(注意:取,)
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)求足球第二次飞出到落地时,该抛物线的表达式.
参考答案
一、选择题(共30分)
1.解:A.方程x2=x是一元二次方程,符合题意;
B.当a=0时,该方程不是一元二次方程,故该选项不符合题意;
C.xy=1是二元二次方程,不符合题意;
D.方x+=1是分式方程,不符合题意.
故选:A.
2.解:由原方程,得
2x﹣4x2=10x﹣5x2﹣3,
则x2﹣8x+3=0.
故选:C.
3.解:抛物线y=2(x﹣3)2+2的顶点坐标是(3,2),
故选:B.
4.解:x(x﹣2)+(x﹣2)=0,
(x﹣2)(x+1)=0,
x﹣2=0或x+1=0,
所以x1=2,x2=﹣1.
故选:D.
5.解:∵x2﹣7x+12=0,
∴(x﹣3)(x﹣4)=0,
∴x﹣3=0或x﹣4=0,
解得:x1=3,x2=4,
∴等腰三角形的两边长分别3或4;
∴该等腰三角形的底边长为3或4;
故选:D.
6.解:由实数a,b满足条件a2﹣7a+2=0,b2﹣7b+2=0,
∴可把a,b看成是方程x2﹣7x+2=0的两个根,
∴a+b=7,ab=2,
∴====.
故选:A.
7.解:当k>0时,函数y=kx﹣2的图象经过一、三、四象限;函数y=kx2的开口向上,对称轴在y轴上;
当k<0时,函数y=kx﹣2的图象经过二、三、四象限;函数y=kx2的开口向下,对称轴在y轴上,故C正确.
故选:C.
8.解:选项A,∵抛物线开口向上,
∴a>0.
∵抛物线的对称轴为x=﹣1,
∴﹣=﹣1,即b=2a.
∴b>0.故选项A错误;
选项B,∵抛物线y=ax2+bx+c与x轴有两个公共点,
∴一元二次方程ax2+bx+c=0有两个不等的实数根.
∴b2﹣4ac>0.故选项B错误;
选项C,由题图可知,当x=﹣1时,抛物线有最低点,且在x轴下方,
∴二次函数有最小值,且y最小<0.
∴当x=﹣1时,二次函数的值y=a﹣b+c<0.故选项C正确;
选项D,由图可知,当x<﹣1时,y随x的增大而减小,当﹣1<x<0时,y随x的增大而增大.
∴当x<0时,y随x增大而减小是错误的,故选项D错误.
故选:C.
9.解:关于x的一元二次方程a(x+2)(x﹣1)+b=0(a<0,b>0)的解就是函数y=a(x+2)(x﹣1)与y=﹣b的交点的横坐标,
∵a<0,
∴抛物线开口向下,
∵b<0,
∴y=﹣b在x轴下方,
∵x1<x2,
如图所示:
∴x1<﹣2<1<x2,
故选:D.
10.解:本题的运动过程应分两部分,从开始到两三角形重合,另一部分是从重合到分离;
在第一部分,三角形ABC在直线MF上向右做匀速运动,则重合部分面积的增加速度不断变快;而另一部分面积的减小速度越来越小.
故选:C.
二、填空题(共12分)
11.解:∵开口向下且过点(0,﹣1)的抛物线解析式,
∴可以设顶点坐标为(0,﹣1),
故解析式为:y=﹣x2﹣1(答案不唯一).
故答案为:y=﹣x2﹣1(答案不唯一).
12.解:∵关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,
∴Δ=b2﹣4ac=(﹣2)2﹣4×k×(﹣1)=4+4k>0,
∴k>﹣1,
∵x的一元二次方程kx2﹣2x﹣1=0
∴k≠0,
∴k的取值范围是:k>﹣1且k≠0.
故答案为:k>﹣1且k≠0.
13.解:∵α方程x2+3x﹣1=0的实数根,
∴α2+3α﹣1=0,
∴α2=﹣3α+1,
∴α2+2α﹣β=﹣3α+1+2α﹣β
=﹣(α+β)+1,
∵α、β是方程x2+3x﹣1=0的两个实数根,
∴α+β=﹣3,
∴α2+2α﹣β=3+1=4.
故答案为4.
14.解:(1)由ax2+(b﹣1)x+c=0,得ax2+bx+c=x,
可知二次函数y=ax2+bx+c与一次函数y=x的交点为(﹣1,﹣1)和(3,3),
所以方程ax2+bx+c=x的根是x1=﹣1,x2=3;
(2)根据表格可知抛物线的对称轴是,当时,函数值y随着x的增大而增大,
∴抛物线开口向下.
,
解得x=4,
可知当x=﹣1和x=4时,y=﹣1.
∴当﹣1<x<4时,ax2+bx+c>﹣1.
故答案为:﹣1,3;﹣1<x<4.
三、解答题(满分78分)
15.解方程:2x2﹣x﹣1=0,
(x﹣1)(2x+1)=0,
x﹣1=0,2x+1=0,
∴.
16.解:设方程的另一根为x2.
∵关于x的一元二次方程x2﹣6x+m2﹣3m﹣5=0的一个根是﹣1,
∴x=﹣1满足关于x的一元二次方程x2﹣6x+m2﹣3m﹣5=0,
∴(﹣1)2﹣6×(﹣1)+m2﹣3m﹣5=0,即m2﹣3m+2=0,
∴(m﹣1)(m﹣2)=0,
解得,m=1或m=2;
又由韦达定理知﹣1+x2=6,
解得,x2=7.即方程的另一根是7.
17.解:把A(﹣2,5),点(2,﹣3)代入y=x2+bx+c得,解得,
所以二次函数的解析式为y=x2﹣2x﹣3;
当x=0时,y=0﹣0﹣3=﹣3,
所以点B(0,3)不在这个函数的图象上.
18.解:(1)把点(﹣2,﹣5)、点(1,4)、点(0,3)代入得,
,
解得,
∴;
把点(﹣2,﹣5)和点(1,4)代入y2=mx+n得,
解得,
∴y2=3x+1.
(2)如图,在同一坐标系中画出和y2=3x+1的图象,
由图象可得①当﹣2<x<1时,y1>y2;②当x=﹣2或x=1时,y1=y2;③当x>1或x<﹣2时,y1<y2.
19.解:设宽为x m,则长为(16﹣2x)m.
由题意,得 x (16﹣2x)=30,
解得 x1=3,x2=5.
当x=3时,16﹣2×3=10,
当x=5时,16﹣2×5=6.
答:围成矩形的长为10 m、宽为3 m,或长为6 m、宽为5m.
20.解:(1)∵关于x的一元二次方程mx2﹣2mx+m﹣2=0有两个实数根,
∴m≠0且△≥0,即(﹣2m)2﹣4 m (m﹣2)≥0,
解得m≠0且m≥0,
∴m的取值范围为m>0.
(2)∵方程两实根为x1,x2,
∴x1+x2=2,x1 x2=,
∵|x1﹣x2|=1,
∴(x1﹣x2)2=1,
∴(x1+x2)2﹣4x1x2=1,
∴22﹣4×=1,
解得:m=8;
经检验m=8是原方程的解.
21.解:(1)∵CD⊥y轴,
∴C,D两点关于抛物线对称轴对称D(6,4),
∴C(0,4),
∴此抛物线的对称轴为直线:,即x=3
(2)连接AC,
∵A,B关于对称轴对称,B(8,0),
抛物线的对称轴为直线:x=3,
∴A(﹣2,0),
∴AB=8﹣(﹣2)=10,
∴△ABC的面积=.
22.解:设新品种花生产量的增长率为x,则新品种花生出油率的增长率为x,
根据题意得:3000(1+x)×50%(1+x)=1980,
整理得:x2+3x﹣0.64=0,
解得:x1=0.2=20%,x2=﹣3.2(不符合题意,舍去).
答:新品种花生产量的增长率为20%.
23.解:(1)由题意知,A(0,1),B(6,0),顶点坐标M(6,4),
设足球开始飞出到第一次落地时,抛物线的表达式为y=a(x﹣6)2+4,
将A(0,1)代入得,1=a(0﹣6)2+4,
解得,
∴,
∴足球开始飞出到第一次落地时,抛物线的表达式为;
(2)当y=0时,,
解得:,(不合题意,舍去),
∴C(13,0),
由题意,设第二次落地的抛物线的顶点坐标为(k,2),设第二次落地的抛物线为,
当x=13时,,
解得,(不合题意,舍去),
∴,
∴足球第二次飞出到落地时,抛物线的表达式为.
同课章节目录
