苏教版(2019)必修第一册 第八章《函数应用》同步练习(含解析)
文档属性
| 名称 | 苏教版(2019)必修第一册 第八章《函数应用》同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 758.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 13:03:26 | ||
图片预览




文档简介
专题练习《函数应用》
一.选择题(共12小题)
1.充电电池是电动汽车的核心部件之一,如何提高充电速度是电池制造商重点关注的研究方向.已知电池充入的电量E(单位:kW h)与充电时间t(单位:min)满足函数E(t)=M(1﹣e﹣kt),其中M表示电池的容量,k表示电池的充电效率.研究人员对A,B两个型号的电池进行充电测试,电池A的容量为80kW h,充电30min充入了40kW h的电量;电池B的容量为60kW h,充电15min充入了20kW h的电量.设电池A的充电效率为k1,电池B的充电效率为k2,则( )
A.k1>k2
B.k1<k2
C.k1=k2
D.k1,k2大小关系无法确定
2.折纸是我国民间的一种传统手工艺术.现有一张长10cm、宽8cm的长方形的纸片,将纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1,S2.若S1:S2=1:3,则折痕长的最大值为( )
A.cm B.10cm C.2cm D.2cm
3.某科技有限公司为了鼓励员工创新,打破发达国家的芯片垄断,计划逐年增加研发资金投入,若该公司2018年全年投入的研发资金为200万元,在此基础上,每年投入的研发资金比上一年增加10%,则该公司全年投入的研发资金开始超过400万元的年份是( )
(参考数据:1.16=1.77,1.17=1.95,1.18=2.14,1.19=2.36)
A.2024年 B.2025年 C.2026年 D.2027年
4.若某商店将进货单价为6元的商品按每件10元出售,则每天可销售100件,现准备采用提高售价、减少进货量的方法来增加利润.已知这种商品的售价每提高1元,销售量就要减少10件,那么要保证该商品每天的利润在450元以上,售价应定为( )
A.11元 B.11元到15元之间
C.15元 D.10元到14元之间
5.唐代诗人李顾的诗《古从军行》开头两句说“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为x2+y2≤1,若将军从点A(3,0)处出发,河岸线所在直线方程为x+y=4,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A. B.2 C. D.
6.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在地为点B(﹣2,3),若将军从点A(2,0)处出发,河岸线所在直线方程为x+y=3,则“将军饮马”的最短总路程为( )
A. B. C. D.
7.要测定古物的年代,可以用放射性碳法:在动植物的体内都含有微量的放射性14C,动植物死亡后,停止新陈代谢,14C不再产生,且原有的14C会自动衰变.经科学测定,14C的半衰期为5730(设14C的原始量为1,经过x年后,14C的含量f(x)=ax,即f(5730)=).现有一古物,测得14C为原始量的79.37%,则该古物距今约多少年?( )(参考数据:≈0.7937,≈0.9998)
A.1910 B.3581 C.9168 D.17190
8.Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为( )(参考数据ln19≈3)
A.60 B.62 C.66 D.63
9.有一组实验数据如表所示:
x 2.01 3 4.01 5.1 6.12
y 3 8.01 15 23.8 36.04
则最能体现这组数据关系的函数模型是( )
A.y=2x+1﹣1 B.y=x2﹣1 C.y=2log2x D.y=x3
10.已知函数f(x)=,在下列区间中,包含f(x)的零点的区间是( )
A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)
11.冈珀茨模型(y=ka)是由冈珀茨(Gompertz)提出,可作为动物种群数量变化的模型,并用于描述种群的消亡规律.已知某珍稀物种t年后的种群数量y近似满足冈珀茨模型:y=k0 e(当t=0时,表示2020年初的种群数量),若m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,则m的最小值为( )(ln2≈0.7)
A.5 B.6 C.7 D.8
12.某高校为加强学科建设,制定了第“十四五”(2021﹣2025)规划,计划逐年加大科研资金投入,已知该校计划2021年全年投入科研资金20万元,2025年全年投入科研资金28万元,则第“十四五”期间,投入科研资金的年均增长率约为( )
A.1.4﹣1 B.1.4﹣1 C.log1.45﹣1 D.log1.44﹣1
二.填空题(共4小题)
13.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量变为原来的一半所经历的时间称为它的半衰期,记为.现测得某种放射性元素的剩余质量A随时间t变化的6次数据如表:
t(单位时间) 0 2 4 6 8 10
A(t) 320 226 160 115 80 57
从以上记录可知这种元素的半衰期约为 个单位时间,剩余质量随时间变化的衰变公式为A(t)= .
14.为了参加校教职工运动会,某校高三年级组准备为本年级教师订制若干件文化衫,经与厂家协商,可按出厂价结算,同时厂家也承诺超过50件就可以每件比出厂价低22元给予优惠.如果按出厂价购买年级组总共应付a元,但若再多买15件就可以达到优惠条件并恰好也是共付a元(a为整数),则a的值为 .
15.某地在20年间经济高质量增长,GDP的值P(单位:亿元)与时间t(单位:年)之间的关系为P(t)=P(1+10%)t,其中P为t=0时的P值.假定P=2,那么在t=10时,GDP增长的速度大约是 .(单位:亿元/年,精确到0.01亿元/年)注:1.110≈2.59,当x取很小的正数时,ln(1+x)≈x.
16.根据国家统计局发布的第七次全国人口普查结果显示,截止2020年底,我国总人口数约为14亿,同2010年第六次全国人口普查数据相比,年平均增长率约为0.53%.若按此增长率,30年后我国人口总数约为 亿;为应对人口老龄化带来的挑战,改善我国人口结构,保持我国人力资源禀赋优势,党中央进一步优化了生育政策:若希望30年后,在中华人民共和国建国百年左右,我国人口超过20亿,那么人口年平均增长率应不低于 %.(精确到0.1)(参考数据:1.005330≈1.1718,100.005≈1.0116,lg7≈0.85)
三.解答题(共5小题)
17.筒车是我国古代发明的一种水利灌溉工具,因其经济环保,至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中描绘了筒车的工作原理,如图1是一个半径为R(单位:米),有24个盛水筒的筒车,按逆时针方向匀速旋转,转一周需要120秒,为了研究某个盛水筒P离水面高度h(单位:米)与时间t(单位:秒)的变化关系,建立如图2所示的平面直角坐标系xOy.已知t=0时P的初始位置为点A(2,﹣2)(此时P装满水).
(1)P从出发到开始倒水入槽需要用时40秒,求此刻P距离水面的高度(结果精确到0.1);
(2)记与P相邻的下一个盛水筒为Q,在筒车旋转一周的过程中,求P与Q距离水面高度差的最大值(结果精确到0.1).
18.有四个小镇恰好位于边长为10千米的菱形ABCD的四个顶点处.政府拟建公路连通四个小镇,若每千米公路的建设成本是10万元,预算为280万元,原计划按照菱形ABCD对角线修路.
(1)若预算刚好花完,求菱形ABCD的面积;
(2)若ABCD为正方形,施工队发现按照原计划修路会预算不足,于是采取如下新方案:按如图实线所示修路,其中AM=BM=CN=DN,∠BAM=θ,θ∈(0,),问:新方案能否在预算内完成修路目标?求出新方案的最低花费.
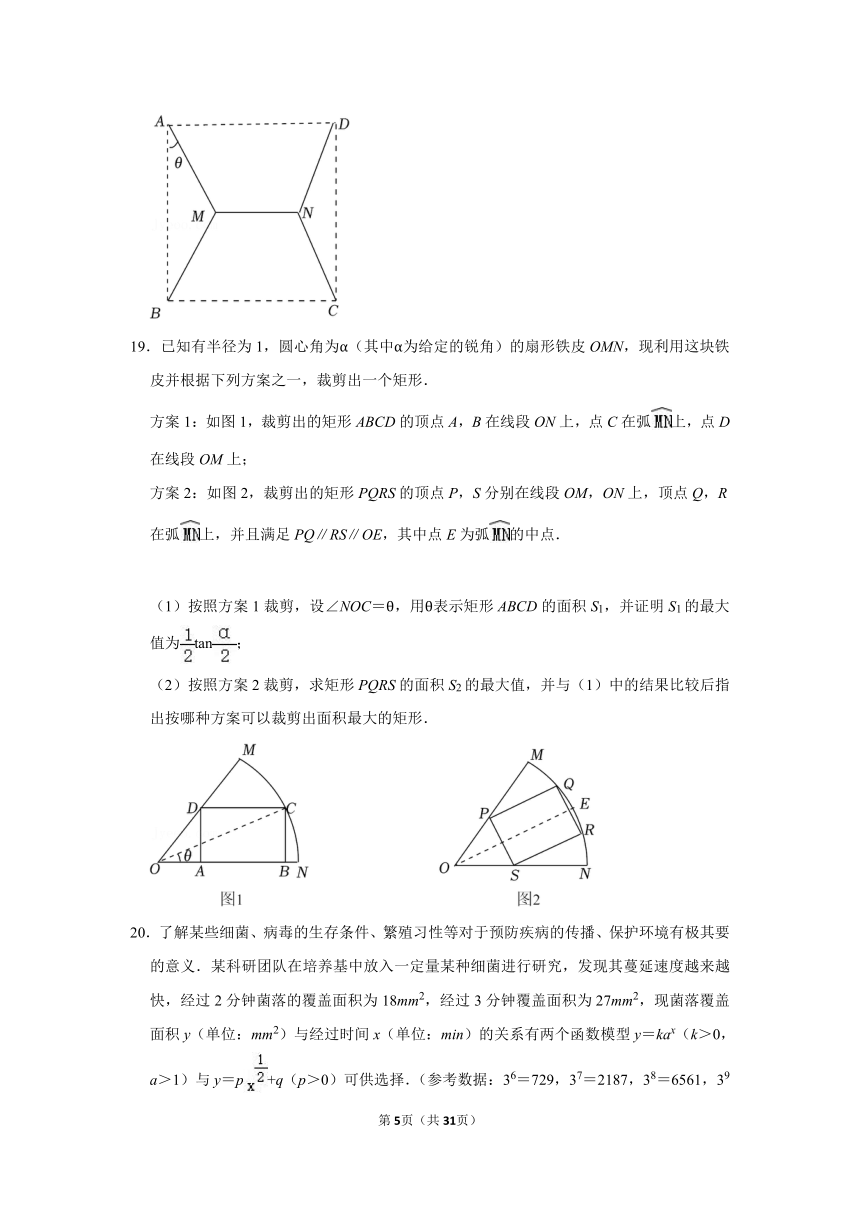
19.已知有半径为1,圆心角为α(其中α为给定的锐角)的扇形铁皮OMN,现利用这块铁皮并根据下列方案之一,裁剪出一个矩形.
方案1:如图1,裁剪出的矩形ABCD的顶点A,B在线段ON上,点C在弧上,点D在线段OM上;
方案2:如图2,裁剪出的矩形PQRS的顶点P,S分别在线段OM,ON上,顶点Q,R在弧上,并且满足PQ∥RS∥OE,其中点E为弧的中点.
(1)按照方案1裁剪,设∠NOC=θ,用θ表示矩形ABCD的面积S1,并证明S1的最大值为tan;
(2)按照方案2裁剪,求矩形PQRS的面积S2的最大值,并与(1)中的结果比较后指出按哪种方案可以裁剪出面积最大的矩形.
20.了解某些细菌、病毒的生存条件、繁殖习性等对于预防疾病的传播、保护环境有极其要的意义.某科研团队在培养基中放入一定量某种细菌进行研究,发现其蔓延速度越来越快,经过2分钟菌落的覆盖面积为18mm2,经过3分钟覆盖面积为27mm2,现菌落覆盖面积y(单位:mm2)与经过时间x(单位:min)的关系有两个函数模型y=kax(k>0,a>1)与y=p+q(p>0)可供选择.(参考数据:36=729,37=2187,38=6561,39=19683,≈1.414,≈1.732.)
(1)试判断哪个函数模型更合适,说明理由,并求出该模型的解析式;
(2)在理想状态下,至少经过多久培养基中菌落面积能超过200mm2?(计算结果保留到整数)
21.某企业采用新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=﹣200x+80000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
专题练习《函数应用》
参考答案与试题解析
一.选择题(共12小题)
1.充电电池是电动汽车的核心部件之一,如何提高充电速度是电池制造商重点关注的研究方向.已知电池充入的电量E(单位:kW h)与充电时间t(单位:min)满足函数E(t)=M(1﹣e﹣kt),其中M表示电池的容量,k表示电池的充电效率.研究人员对A,B两个型号的电池进行充电测试,电池A的容量为80kW h,充电30min充入了40kW h的电量;电池B的容量为60kW h,充电15min充入了20kW h的电量.设电池A的充电效率为k1,电池B的充电效率为k2,则( )
A.k1>k2
B.k1<k2
C.k1=k2
D.k1,k2大小关系无法确定
【考点】根据实际问题选择函数类型.【专题】计算题;方程思想;综合法;函数的性质及应用;逻辑推理;数学运算.
【分析】列出方程后比较k1,k2大小.
【解答】解:由题意得,则,
同理,则,得,
由指数函数单调性得﹣30k2<﹣30k1,即k1<k2.
故选:B.
【点评】本题主要考查函数模型及其应用,属于基础题.
2.折纸是我国民间的一种传统手工艺术.现有一张长10cm、宽8cm的长方形的纸片,将纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1,S2.若S1:S2=1:3,则折痕长的最大值为( )
A.cm B.10cm C.2cm D.2cm
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;分析法;函数的性质及应用;数学运算.
【分析】由已知可确定,分别在三种折叠方式下利用面积建立关于折痕的函数关系式,根据二次函数和对勾函数的单调性可求得最值,由此可得结果.
【解答】解:由题意得:长方形纸片的面积为 10×8=80(cm2),又 S1:S2=1:3,
∴,
①当折痕如下图所示时,
设AM=x,AN=y,则,解得:,∴,
②当折痕如下图所示时,
设AN=x,DM=y,则 ,解得:,
∵f(t) 在 (25,40)上单调递减,在 (40,100)上单调递增,
又 ,∴g(x)∈[64,89],
∴,
③当折痕如下图所示时,
设AF=x,BE=y,则 ,解得:,
∴EF2=(x﹣y)2+100=(2x﹣4)2+100,
令h(x)=(2x﹣4)2+100(0≤x≤4),则h(x)在(0,2)上单调递减,在(2,4)上单调递增,
又h(0)=16+100=116,h(2)=100,h(4)=16+100=116,∴h(x)∈[100,116],
∴;
综上所述:折痕长的取值范围为;
∴折痕长的最大值为.
故选:C.
【点评】本题考查函数的实际应用,考查学生的运算能力,属于中档题.
3.某科技有限公司为了鼓励员工创新,打破发达国家的芯片垄断,计划逐年增加研发资金投入,若该公司2018年全年投入的研发资金为200万元,在此基础上,每年投入的研发资金比上一年增加10%,则该公司全年投入的研发资金开始超过400万元的年份是( )
(参考数据:1.16=1.77,1.17=1.95,1.18=2.14,1.19=2.36)
A.2024年 B.2025年 C.2026年 D.2027年
【考点】根据实际问题选择函数类型.【专题】函数思想;数学模型法;函数的性质及应用;逻辑推理.
【分析】设第n年开始400万元,由题意,列出关于n的不等式,求解即可.
【解答】解:设第n年开始超过400万元,
则200×(1+10%)n﹣2018>400,即1.1n﹣2018>2,
因为1.17=1.95,1.18=2.14,
所以当n﹣2018=8,即n=2026时,该公司全年投入的研发资金开始超过400万元.
故选:C.
【点评】本题考查了函数模型的选择与应用,解题的关键是建立符合条件的函数模型,分析清楚问题的逻辑关系是解题的关键,此类问题求解的一般步骤是:建立函数模型,进行函数计算,得出结果,再将结果反馈到实际问题中指导解决问题,考查了逻辑推理能力与化简运算能力,属于中档题.
4.若某商店将进货单价为6元的商品按每件10元出售,则每天可销售100件,现准备采用提高售价、减少进货量的方法来增加利润.已知这种商品的售价每提高1元,销售量就要减少10件,那么要保证该商品每天的利润在450元以上,售价应定为( )
A.11元 B.11元到15元之间
C.15元 D.10元到14元之间
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;分析法;函数的性质及应用;数学运算.
【分析】由题意列出关于利润的解析式,再求利润在450元以上的x的范围.
【解答】解:设每件商品的售价提高x(0<x<10)元,
则每件获得利润(4+x)元,每天可销售(100﹣10x)件.
设该商品每天的利润为y元,则
由题意有y=(4+x)(100﹣10x)=﹣10x2+60x+400,
要保证每天的利润在450元以上,
则﹣10x2+60x+400>450,x ﹣6+5<0,
得1<x<5,
故每件商品的售价在11元到15元之间时,能确保该商品每天的利润在450元以上.
故选:B.
【点评】本题考查函数在实际生活中的应用,属于中档题.
5.唐代诗人李顾的诗《古从军行》开头两句说“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为x2+y2≤1,若将军从点A(3,0)处出发,河岸线所在直线方程为x+y=4,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A. B.2 C. D.
【考点】根据实际问题选择函数类型;与直线关于点、直线对称的直线方程.
【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】设点A关于直线x+y=4的对称性A'(a,b),军营所在区域的圆心为C,则A'C﹣1为最短总路程,再结合A与A’关于直线x+y=4对称,求出A'的坐标,再结合两点之间的距离公式,即可求解.
【解答】解:设点A关于直线x+y=4的对称性A'(a,b),军营所在区域的圆心为C,
则A'C﹣1为最短总路程,
AA'的中点为(),直线AA'的斜率为1,
故直线AA'为y=x﹣3,
由,解得a=4,b=1,
所以A'C=,即A'C=.
故选:D.
【点评】本题主要考查函数的实际应用,考查计算能力,属于中档题.
6.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在地为点B(﹣2,3),若将军从点A(2,0)处出发,河岸线所在直线方程为x+y=3,则“将军饮马”的最短总路程为( )
A. B. C. D.
【考点】根据实际问题选择函数类型.【专题】转化思想;转化法;直线与圆;逻辑推理;数学运算.
【分析】利用点关于点的对称点的求法,求出点A关于直线x+y=3的对称点A',由三点共线取得最小值,结合两点间距离公式求解即可.
【解答】解:由题意可知,点A(2,0),
则点A(2,0)关于直线x+y=3的对称点为A'(a,b),
则,解得a=3,b=1,
故A'(3,1),
又军营所在地为点B(﹣2,3),
所以“将军饮马”的最短总路程为|A'B|=.
故选:C.
【点评】本题考查了直线在实际生活中的应用,点关于直线的对称点的求解,两点间斜率公式以及两点间距离公式的应用,两条直线垂直的充要条件的运用,考查了逻辑推理能力与化简运算能力,属于中档题.
7.要测定古物的年代,可以用放射性碳法:在动植物的体内都含有微量的放射性14C,动植物死亡后,停止新陈代谢,14C不再产生,且原有的14C会自动衰变.经科学测定,14C的半衰期为5730(设14C的原始量为1,经过x年后,14C的含量f(x)=ax,即f(5730)=).现有一古物,测得14C为原始量的79.37%,则该古物距今约多少年?( )(参考数据:≈0.7937,≈0.9998)
A.1910 B.3581 C.9168 D.17190
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;综合法;函数的性质及应用;数学运算.
【分析】由f(5730)=可得,令f(x)=0.7937,得x=loga0.7937,利用换底公式结合对数的运算性质即可求出x的值.
【解答】解:设14C的原始量为1,经过x年后,14C的含量f(x)=ax,
由题意可知:f(5730)=,即,
∴,
令f(x)=0.7937,得:ax=0.7937,
∴x=loga0.7937=====1910,
∴该古物距今约1910年.
故选:A.
【点评】本题主要考查了函数的实际应用,考查了对数的运算,是中档题.
8.Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为( )(参考数据ln19≈3)
A.60 B.62 C.66 D.63
【考点】根据实际问题选择函数类型.【专题】函数思想;数学模型法;函数的性质及应用;数学建模.
【分析】根据所给材料的公式列出方程=0.95K,解出t即可.
【解答】解:由已知可得=0.95K,解得e﹣0.23(t*﹣50)=,
两边取对数有﹣0.23(t*﹣50)=﹣ln19,
解得t*≈63,
故选:D.
【点评】本题考查函数模型的实际应用,考查学生计算能力,是基础题.
9.有一组实验数据如表所示:
x 2.01 3 4.01 5.1 6.12
y 3 8.01 15 23.8 36.04
则最能体现这组数据关系的函数模型是( )
A.y=2x+1﹣1 B.y=x2﹣1 C.y=2log2x D.y=x3
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;方程思想;转化思想;函数的性质及应用.
【分析】利用函数的表格关系判断函数的解析式的可能性,然后验证求解即可.
【解答】解:由函数的表格可知,函数的解析式应该是指数函数类型与二次函数的类型,选项C不正确;
当x=2.01时,y=2x+1﹣1>4;y=x2﹣1≈3,y=x3>7,
当x=3时,y=2x+1﹣1=15;y=x2﹣1≈8,y=x3=27,
故选:B.
【点评】本题考查函数的解析式的判断与应用,函数的模型的应用,是基础题.
10.已知函数f(x)=,在下列区间中,包含f(x)的零点的区间是( )
A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)
【考点】二分法的定义与应用.【专题】计算题;函数思想;定义法;函数的性质及应用.
【分析】函数f(x)在其定义域上连续,同时可判断f(4)<0,f(2)>0;从而判断.
【解答】解:函数f(x)=f(x)=,在其定义域上连续,
f(4)=﹣2<0,
f(2)=3﹣1>0;
故函数f(x)的零点在区间(2,4)上,
故选:C.
【点评】本题考查了函数的零点的判断与应用,属于基础题.
11.冈珀茨模型(y=ka)是由冈珀茨(Gompertz)提出,可作为动物种群数量变化的模型,并用于描述种群的消亡规律.已知某珍稀物种t年后的种群数量y近似满足冈珀茨模型:y=k0 e(当t=0时,表示2020年初的种群数量),若m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,则m的最小值为( )(ln2≈0.7)
A.5 B.6 C.7 D.8
【考点】根据实际问题选择函数类型;对数的运算性质
转化思想;转化法;函数的性质及应用;数学运算.
【分析】由已知条件可得,当t=0时,y=,当t=m时,y=,由m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,可得<,再结合对数函数的公式,即可求解.
【解答】解:∵y=k0 e,
当t=0时,y=,
∴当t=m时,y=,
∵m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,
∴<,
由题可知,k0 是大于0的常数,即2 ,两边取对数可得,ln2+1.4e﹣0.125m<1.4,
∵ln2≈0.7,
∴,两边取对数可得,﹣0.125m<﹣ln2≈﹣0.7,解得m>5.6,m∈N*,
故m的最小值为6.
故选:B.
【点评】本题主要考查函数的实际应用,掌握对数函数的公式是解本题的关键,属于中档题.
12.某高校为加强学科建设,制定了第“十四五”(2021﹣2025)规划,计划逐年加大科研资金投入,已知该校计划2021年全年投入科研资金20万元,2025年全年投入科研资金28万元,则第“十四五”期间,投入科研资金的年均增长率约为( )
A.1.4﹣1 B.1.4﹣1 C.log1.45﹣1 D.log1.44﹣1
【考点】根据实际问题选择函数类型;指数函数的图象与性质.【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】设年增长率为x,由题意可得,20(1+x)4=28,解出x的取值范围,即可求解.
【解答】解:设年增长率为x,由题意可得,20(1+x)4=28,即,
所以,解得x=,
故投入科研资金的年均增长率约为.
故选:A.
【点评】本题主要考查函数的实际应用,掌握指数函数的公式是解本题的关键,属于基础题.
二.填空题(共4小题)
13.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量变为原来的一半所经历的时间称为它的半衰期,记为.现测得某种放射性元素的剩余质量A随时间t变化的6次数据如表:
t(单位时间) 0 2 4 6 8 10
A(t) 320 226 160 115 80 57
从以上记录可知这种元素的半衰期约为 4 个单位时间,剩余质量随时间变化的衰变公式为A(t)= (t≥0) .
【考点】根据实际问题选择函数类型.【专题】转化思想;分析法;函数的性质及应用;数学运算.
【分析】首先观察表格,根据半衰期的定义,可得半衰期为4个单元时间,初始质量为A(0)=320,根据题意可知此模型是指数函数模型,且底数为,指数为经过的时间除以半衰期,结合初始质量,即可求解.
【解答】解:从题表中数据易知半衰期为4个单位时间,由初始质量为A0=320,则经过时间t的剩余质量为A(t)==(t≥0).
(t≥0).
故答案为:4,(t≥0).
【点评】本题考查了函数模型的实际应用,关键是理解半衰期的定义,属于基础题.
14.为了参加校教职工运动会,某校高三年级组准备为本年级教师订制若干件文化衫,经与厂家协商,可按出厂价结算,同时厂家也承诺超过50件就可以每件比出厂价低22元给予优惠.如果按出厂价购买年级组总共应付a元,但若再多买15件就可以达到优惠条件并恰好也是共付a元(a为整数),则a的值为 3960 .
【考点】根据实际问题选择函数类型.【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】设按出厂价购买x(x≤50)套,应付a元,出厂价为y元,则有a=xy (x≤50)①,再多买15套,就可以按优惠价结算恰好也付a元,则有a=(x+15)(y﹣22)(x+15>50)②,联立①②,再结合x,a为整数,即可求解.
【解答】解:设按出厂价购买x(x≤50)套,应付a元,出厂价为y元,
则有a=xy (x≤50)①,
再多买15套,就可以按优惠价结算恰好也付a元,
则有a=(x+15)(y﹣22)(x+15>50)②,
联立①②可得,xy=xy+15y﹣22x﹣330,即y=(35<x≤50),
∵x为整数,a为整数,
∴x=45,y=88,
故a=xy=45×88=3960.
故答案为:3960.
【点评】本题主要考查函数的实际应用,考查计算能力,属于基础题.
15.某地在20年间经济高质量增长,GDP的值P(单位:亿元)与时间t(单位:年)之间的关系为P(t)=P(1+10%)t,其中P为t=0时的P值.假定P=2,那么在t=10时,GDP增长的速度大约是 0.52 .(单位:亿元/年,精确到0.01亿元/年)注:1.110≈2.59,当x取很小的正数时,ln(1+x)≈x.
【考点】根据实际问题选择函数类型.【专题】计算题;方程思想;综合法;函数的性质及应用;逻辑推理;数学运算.
【分析】由题可得GDP增长的速度为P'(t)=2×1.1tln1.1,进而即得.
【解答】解:由题可知P(t)=2(1+10%)t=2×1.1t,
所以P'(t)=2×1.1tln1.1,
所以P'(10)=2×1.110ln1.1≈2×2.59×0.1=0.518≈0.52,
即GDP增长的速度大约是0.52.
故答案为:0.52.
【点评】本题主要考查函数模型及其应用,对数及其近似运算等知识,属于基础题.
16.根据国家统计局发布的第七次全国人口普查结果显示,截止2020年底,我国总人口数约为14亿,同2010年第六次全国人口普查数据相比,年平均增长率约为0.53%.若按此增长率,30年后我国人口总数约为 16.4 亿;为应对人口老龄化带来的挑战,改善我国人口结构,保持我国人力资源禀赋优势,党中央进一步优化了生育政策:若希望30年后,在中华人民共和国建国百年左右,我国人口超过20亿,那么人口年平均增长率应不低于 1.2 %.(精确到0.1)(参考数据:1.005330≈1.1718,100.005≈1.0116,lg7≈0.85)
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;定义法;函数的性质及应用;数学建模;数学运算.
【分析】根据年平均增长率约为0.53%求解;设年平均增长率为p,由14(1+p)30>20求解
【解答】解:因为2020年底,我国总人口数约为14亿,且年平均增长率约为0.53%,
所以30年后我国人口总数约为 14(1+0.53%)30=14×1.005330≈14×1.1718=16.4;
设年平均增长率为 p,
由题意得:14(1+p)30>20,
则 ,
两边取对数得 30lg(1+p)>1﹣lg7≈0.15,
即lg(1+p)>0.005,
所以 1+p>100.005≈1.0116,
解得 p>0.0116,
所以人口年平均增长率应不低于 1.2%,
故答案为:16.4,1.2.
【点评】本题考查指数运算,考查指数方程的解法,考查数学建模和数学运算的核心素养,属于基础题.
三.解答题(共5小题)
17.筒车是我国古代发明的一种水利灌溉工具,因其经济环保,至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中描绘了筒车的工作原理,如图1是一个半径为R(单位:米),有24个盛水筒的筒车,按逆时针方向匀速旋转,转一周需要120秒,为了研究某个盛水筒P离水面高度h(单位:米)与时间t(单位:秒)的变化关系,建立如图2所示的平面直角坐标系xOy.已知t=0时P的初始位置为点A(2,﹣2)(此时P装满水).
(1)P从出发到开始倒水入槽需要用时40秒,求此刻P距离水面的高度(结果精确到0.1);
(2)记与P相邻的下一个盛水筒为Q,在筒车旋转一周的过程中,求P与Q距离水面高度差的最大值(结果精确到0.1).
【考点】根据实际问题选择函数类型;三角函数模型的应用.【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】(1)根据已知条件,先求出线段OA按逆时针方向旋转了,再结合A点的坐标,即可求解.
(2)根据已知条件,分别求出P开始转动t秒后距离水面的高度h1,Q距离水面的高度h2,则P,Q距离水面的高度差H=|h1﹣h2|,再结合三角函数的恒等变换,即可求解.
【解答】解:(1)由于筒车转一周需要120秒,
所以P从出发到开始倒水入槽的40秒,线段OA按逆时针方向旋转了,
因为A点坐标为(2,﹣2),则,以OA为终边的角为,
所以P距离水面的高度为≈6.9m.
(2)由于筒车转一周需要120秒,可知P转动的角度为,
又以OA为终边的角为,
则P开始转动t秒后距离水面的高度,0≤t≤120,
如图所示,
P,Q两个盛水筒分别用点B,C表示,
则,点C相对于点B始终落后rad,
此时Q距离水面的高度,
则P,Q距离水面的高度差H=|h1﹣h2|==,0≤t≤120,
利用sinθ+sinφ=,可得H=,
当或,解得t=22.5或t=82.5,
故H最大值为,
所以P与Q距离水面高度差的最大值约为1.0m.
【点评】本题主要考查函数的实际应用,考查转化能力,属于难题.
18.有四个小镇恰好位于边长为10千米的菱形ABCD的四个顶点处.政府拟建公路连通四个小镇,若每千米公路的建设成本是10万元,预算为280万元,原计划按照菱形ABCD对角线修路.
(1)若预算刚好花完,求菱形ABCD的面积;
(2)若ABCD为正方形,施工队发现按照原计划修路会预算不足,于是采取如下新方案:按如图实线所示修路,其中AM=BM=CN=DN,∠BAM=θ,θ∈(0,),问:新方案能否在预算内完成修路目标?求出新方案的最低花费.
【考点】根据实际问题选择函数类型.【专题】应用题;函数思想;构造法;三角函数的求值;数学运算.
【分析】(1)设菱形对角线分别为x,y,根据题意求出x、y的关系,再计算菱形ABCD的面积.
(2)延长MN、NM,交AB、CD于点F、G,求出AM+BM+CN+DN+MN的表达式,再构造函数,利用函数求出函数的最小值,即可得出结论.
【解答】解:(1)设菱形对角线分别为x,y,依题意知,x+y==28,
又因为菱形的对角线互相垂直且平分,所以+=102,即x2+y2=400,
所以(x+y)2﹣2xy=400,解得xy=192,
所以菱形ABCD的面积为xy=×192=96(平方米).
(2)
延长MN、NM,交AB、CD于点F、G,如图所示:
因为AM=BM=CN=DN,∠BAM=θ,
所以=cosθ,解得AM=,
所以AM+BM+CN+DN=,
又因为=tanθ=,解得FM=,所以MN=10﹣,
因此总长度为10+10×,
设f(θ)=,θ∈(0,),则f′(θ)=,
当θ∈(0,)时,f′(θ)<0,f(θ)单调递减,
当θ∈(,),f′(θ)>0,f(θ)单调递增;
当θ=时,f(θ)=0,f(θ)取得最小值为f()==,
此时总长度最小,为10+10,对应的总费用为(10+10)×10=100+100<280,
所以新方案能在预算内完成修路目标,且新方案的最低花费为(100+100)万元.
【点评】本题考查了三角函数求值的应用问题,也考查了利用函数求最值问题,是中档题.
19.已知有半径为1,圆心角为α(其中α为给定的锐角)的扇形铁皮OMN,现利用这块铁皮并根据下列方案之一,裁剪出一个矩形.
方案1:如图1,裁剪出的矩形ABCD的顶点A,B在线段ON上,点C在弧上,点D在线段OM上;
方案2:如图2,裁剪出的矩形PQRS的顶点P,S分别在线段OM,ON上,顶点Q,R在弧上,并且满足PQ∥RS∥OE,其中点E为弧的中点.
(1)按照方案1裁剪,设∠NOC=θ,用θ表示矩形ABCD的面积S1,并证明S1的最大值为tan;
(2)按照方案2裁剪,求矩形PQRS的面积S2的最大值,并与(1)中的结果比较后指出按哪种方案可以裁剪出面积最大的矩形.
【考点】根据实际问题选择函数类型.【专题】整体思想;综合法;函数的性质及应用;数学运算.
【分析】(1)分别用含有θ的三角函数表示AD,AB,写出矩形面积,利用三角函数求解最值即可;(2)在图2中,设OE与PS,QR分别交于G,H,则利用(1)的结论,可以得到矩形PQHG的最大面积为,根据对称性,矩形PQRS的最大面积为tan,然后利用作差法比较大小即可.
【解答】解:(1)在图1中,r=1,∠NOC=θ,θ∈(0,α),
AD=BC=rsinθ=sinθ,OB=rcosθ=cosθ,AB=OB﹣OA=OB﹣=cos,
S1=SABCD=sin=(sin2θ﹣)=(sin2)﹣
=﹣=,
当θ=时,矩形ABCD的最大面积为=,
故原结论成立;
(2)在图(2)中,设OE与边PS,QR分别交于点G,H,
则利用(1)的结论,可以得到矩形PQHG的最大面积为,
根据对称性,矩形PQRS的最大面积为tan,
因为α为锐角,所以,
于是0,
因此,=>0,
故按照方案1可以裁剪出面积最大的矩形,其最大面积为.
【点评】本题考查了函数模型的选择以及应用,考查了三角函数的运算以及学生的运算求解能力,属于中档题.
20.2020年,全世界范围内都受到“新冠”疫情的影响.了解某些细菌、病毒的生存条件、繁殖习性等对于预防疾病的传播、保护环境有极其要的意义.某科研团队在培养基中放入一定量某种细菌进行研究,发现其蔓延速度越来越快,经过2分钟菌落的覆盖面积为18mm2,经过3分钟覆盖面积为27mm2,现菌落覆盖面积y(单位:mm2)与经过时间x(单位:min)的关系有两个函数模型y=kax(k>0,a>1)与y=p+q(p>0)可供选择.(参考数据:36=729,37=2187,38=6561,39=19683,≈1.414,≈1.732.)
(1)试判断哪个函数模型更合适,说明理由,并求出该模型的解析式;
(2)在理想状态下,至少经过多久培养基中菌落面积能超过200mm2?(计算结果保留到整数)
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;分析法;函数的性质及应用;数学运算.
【分析】(1)根据函数的单调性可知选哪个模型更合适;
(2)解指数函数不等式可求得答案
【解答】解:(1)y=kax(k>0,a>1)的增长速度越来越快,y=p+q(p>0)的增长速度越来越慢,
根据题意应选y=kax(k>0,a>l),
于是,解得:,
∴y=8()x(x∈N),
(2)根据y=8()x(x∈N)函数模型,可得不等式8()x>200,解得x≥8,
故至少经过8min 培养基中菌落面积能超过200mm2.
【点评】本题考查指数函数模型及其应用,考查了学生的运算能力,属于中档题.
21.某企业采用新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=﹣200x+80000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
【考点】根据实际问题选择函数类型.【专题】函数思想;数学模型法;函数的性质及应用;数学建模.
【分析】(1)由题意列出该单位每月处理量的函数表达式,利用基本不等式求最值;
(2)写出该单位没有的获利f(x)关于x的函数,整理后利用二次函数的单调性求最值,则答案可求.
【解答】解:(1)由题意可知:,
所以,每吨二氧化碳的平均处理成本为,
由基本不等式可得:(元),
当且仅当时,即当x=400时,等号成立,
因此,该单位每月处理量为400吨时,才能使每吨的平均处理成本最低.
(2)令f(x)=100x﹣
=﹣x2+300x﹣80000=,
∵300≤x≤600,函数f(x)在区间[300,600]上单调递减,
∴当x=300时,函数f(x)取得最大值,即f(x)max=f(300)=﹣35000.
所以,该单位每月不能获利,国家至少需要补贴35000元才能使该单位不亏损.
【点评】本题考查函数模型的选择及应用,考查利用基本不等式与配方法求最值。
考点卡片
1.指数函数的图象与性质
【知识点的认识】
1、指数函数y=ax(a>0,且a≠1)的图象和性质:
y=ax a>1 0<a<1
图象
定义域 R
值域 (0,+∞)
性质 过定点(0,1)
当x>0时,y>1;x<0时,0<y<1 当x>0时,0<y<1;x<0时,y>1
在R上是增函数 在R上是减函数
2、底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.
③当a>0,且a≠l时,函数y=ax 与函数y=的图象关于y轴对称.
3、利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值.
2.对数的运算性质
【知识点的认识】
对数的性质:①=N;②logaaN=N(a>0且a≠1).
loga(MN)=logaM+logaN; loga=logaM﹣logaN;
logaMn=nlogaM; loga=logaM.
3.二分法的定义与应用
【二分法的定义】
二分法 即一分为二的方法.设函数f(x)在[a,b]上连续,且满足f(a) f(b)<0,我们假设f(a)<0,f(b)>0,那么当x1=时,若f(x1)=0,这说x1为零点;若不为0,假设大于0,那么继续在[x1,b]区间取中点验证它的函数值为0,一直重复下去,直到找到满足要求的点为止.这就是二分法的基本概念.
【二分法的应用】
我们以具体的例子来说说二分法应用的一个基本条件:
例题:下列函数图象均与x轴有交点,其中能用二分法求函数零点的是
解:能用二分法求函数零点的函数,在零点的左右两侧的函数值符号相反,
有图象可得,只有③能满足此条件,
故答案为 ③.
在这个例题当中,所要求的能力其实就是对概念的理解,这也是二分法它惯用的考查形式,通过这个例题,希望同学们能清楚二分法的概念和常考题型.
【二分法求方程的近似解】
二分法在高中主要属于了解性的内容,拿二分法求近似解思路也比较固定,这里我们主要以例题来做讲解.
例:用二分法求方程在[1,2]上的近似解,取中点c=1.5,则下一个有根区间是 [1.5,2] .
解:令函数f(x)=lnx﹣,由于f(1.5)=ln(1.5)﹣=(ln1.52﹣2)<(lne2﹣2)=0,即f(1.5)<0,
而f(2)=ln2﹣=ln2﹣ln=ln=ln>ln1=0,即f(2)>0,
故函数f(x)在[1.5 2]上存在零点,故方程在[1.5,2]上有根,
故答案为[1.5,2].
通过这个例题,我们可以发现二分法的步奏,第一先确定f(a) f(b)<0的a,b点;第二,寻找区间(a,b)的中点,并判断它的函数值是否为0;第三,若不为0,转第一步.
4.根据实际问题选择函数类型
【知识点的知识】
1.实际问题的函数刻画
在现实世界里,事物之间存在着广泛的联系,许多联系可以用函数刻画.用函数的观点看实际问题,是学习函数的重要内容.
2.用函数模型解决实际问题
(1)数据拟合:
通过一些数据寻求事物规律,往往是通过绘出这些数据在直角坐标系中的点,观察这些点的整体特征,看它们接近我们熟悉的哪一种函数图象,选定函数形式后,将一些数据代入这个函数的一般表达式,求出具体的函数表达式,再做必要的检验,基本符合实际,就可以确定这个函数基本反映了事物规律,这种方法称为数据拟合.
(2)常用到的五种函数模型:
①直线模型:一次函数模型y=kx+b(k≠0),图象增长特点是直线式上升(x的系数k>0),通过图象可以直观地认识它,特例是正比例函数模型y=kx(k>0).
②反比例函数模型:y=(k>0)型,增长特点是y随x的增大而减小.
③指数函数模型:y=a bx+c(b>0,且b≠1,a≠0),其增长特点是随着自变量的增大,函数值增大的速度越来越快(底数b>1,a>0),常形象地称为指数爆炸.
④对数函数模型,即y=mlogax+n(a>0,a≠1,m≠0)型,增长特点是随着自变量的增大,函数值增大越来越慢(底数a>1,m>0).
⑤幂函数模型,即y=a xn+b(a≠0)型,其中最常见的是二次函数模型:y=ax2+bx+c(a≠0),其特点是随着自变量的增大,函数值先减小后增大(a>0).
在以上几种函数模型的选择与建立时,要注意函数图象的直观运用,分析图象特点,分析变量x的范围,同时还要与实际问题结合,如取整等.
3.函数建模
(1)定义:用数学思想、方法、知识解决实际问题的过程,叫作数学建模.
(2)过程:如下图所示.
【典型例题分析】
典例1:某公司为了实现1000万元的利润目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的25%,其中模型能符合公司的要求的是(参考数据:1.003600≈6,1n7≈1.945,1n102≈2.302)( )
A.y=0.025x B.y=1.003xC.y=l+log7x D.y=x2
分析:由题意,符合公司要求的模型只需满足:当x∈[10,1000]时,①函数为增函数;②函数的最大值不超过5;③y≤x 25%,然后一一验证即可.
解答:解:由题意,符合公司要求的模型只需满足:
当x∈[10,1000]时,
①函数为增函数;②函数的最大值不超过5;③y≤x 25%=x,
A中,函数y=0.025x,易知满足①,但当x>200时,y>5不满足公司要求;
B中,函数y=1.003x,易知满足①,但当x>600时,y>5不满足公司要求;
C中,函数y=l+log7x,易知满足①,当x=1000时,y取最大值l+log71000=4﹣lg7<5,且l+log7x≤x恒成立,故满足公司要求;
D中,函数y=x2,易知满足①,当x=400时,y>5不满足公司要求;
故选C
点评:本题以实际问题为载体,考查函数模型的构建,考查方案的优化设计,解题的关键是一一验证.
典例2:某服装生产企业为了占有更多的市场份额,拟在2015年度进行一系列促销活动,经过市场调查和测算,服装的年销量x万件与年促销t万元之间满足关系式3﹣x=(k为常数),如果不搞促销活动,服装的年销量只能是1万件.已知2015年生产服装的设备折旧,维修等固定费用需要3万元,每生产1万件服装需再投入32万元的生产费用,若将每件服装的售价定为:“每件生产成本的150%”与“平均每件促销费的一半”之和,试求:
(1)2015年的利润y(万元)关于促销费t (万元)的函数;
(2)该企业2015年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入﹣生产成本﹣促销费,生产成本=固定费用+生产费用)
分析:(1)通过x表示出年利润y,并化简整理,代入整理即可求出y万元表示为促销费t万元的函数.
(2)根据已知代入(2)的函数,分别进行化简即可用基本不等式求出最值,即促销费投入多少万元时,企业的年利润最大.
解答:解:(1)由题意:3﹣x=,
且当t=0时,x=1.
所以k=2,所以3﹣x=,…(1分)
生产成本为 32x+3,每件售价,…(2分)
所以,y=…(3分)
=16x﹣=,(t≥50);…(2分)
(2)因为 当且仅当,即t=7时取等号,…(4分)
所以y≤50﹣8=42,…(1分)
答:促销费投入7万元时,企业的年利润最大.…(1分)
点评:本小题主要考查函数模型的选择与应用,看出基本不等式在求最值中的应用,考查学生分析问题和解决问题的能力,强调对知识的理解和熟练运用,考查转化思想的应用.
【解题方法点拨】
用函数模型解决实际问题的常见类型及解法:
(1)解函数关系已知的应用题
①确定函数关系式y=f(x)中的参数,求出具体的函数解析式y=f(x);②讨论x与y的对应关系,针对具体的函数去讨论与题目有关的问题;③给出实际问题的解,即根据在函数关系的讨论中所获得的理论参数值给出答案.
(2)解函数关系未知的应用题
①阅读理解题意
看一看可以用什么样的函数模型,初步拟定函数类型;
②抽象函数模型
在理解问题的基础上,把实际问题抽象为函数模型;
③研究函数模型的性质
根据函数模型,结合题目的要求,讨论函数模型的有关性质,获得函数模型的解;
④得出问题的结论
根据函数模型的解,结合实际问题的实际意义和题目的要求,给出实际问题的解.
5.三角函数模型的应用
【知识点的知识】
1. 三角函数模型的简单应用:1)在生活中的应用;2);在建筑学中的应用;3)在航海中的应用;4)在物理学中的应用.
2. 解三角函数应用题的一般步骤:
(1)阅读理解材料:将文字语言转化为符号语言;
(2)建立变量关系:抽象成数学问题,建立变量关系;
(3)讨论变量性质:根据函数性质讨论变量性质;
(4)作出结论.
【解题方法点拨】
1、方法与技巧:
(1)在生产生活中,常常有一些与角有关的最值问题,需要确定以角作为变量的三角函数来解决.
(2)理清题意,分清题目中已知和所求,准确解读题目中的术语和有关名词.
(3)要能根据题意,画出符合题意的图形.
(4)对计算结果,可根据实际情况进行处理.
2、注意:
(1)建立三角函数关系式关键是选择适当的角作为变量.
(2)解决应用问题要注重检验.
(3)选择变量后,要根据题中的条件,确定角的范围.
6.与直线关于点、直线对称的直线方程
【知识点的知识】
点与直线的对称问题:
(l)点关于点对称(中点坐标公式):
点关于点成中心对称的对称中心恰是以这两点为端点的线段的中点,因此中心对称的问题是线段中点坐标公式的应用问题.设P(x0,y0),对称中心为A(a,b),则P关于A的对称点为P′(2a﹣x0,2b﹣y0)
(2)点关于直线成轴对称问题
由轴对称定义知,对称轴即为两对称点连线的“垂直平分线”.利用“垂直”“平分”这两个条件建立方程组,就可求出对称点的坐标.一般情形如下:
设点P(x0,y0),关于直线y=kx+b的对称点为P′(x′,y′),则有
可求出x′,y′.
特殊地,点P(x0,y0)关于直线x=a的对称点为P′(2a﹣x0,y0);点P(x0,y0)关于直线y=b的对称点为P′(x0,2b﹣y0).
(3)线关于点对称(转化为点关于点对称,或代入法,两条直线平行):
(4)线关于线对称(求交点,转化为点关于线对称):
由平面几何知识可知若直线a、b关于直线l对称,它们具有下列几何性质:
①若a、b相交,则l是a、b交角的平分线;
②若点A在直线a上,那么A关于直线l的对称点B一定在直线b上,这时AB⊥l,并且AB的中点D在l上;
③a以l为轴旋转180°,一定与b重合.
第1页(共1页)
一.选择题(共12小题)
1.充电电池是电动汽车的核心部件之一,如何提高充电速度是电池制造商重点关注的研究方向.已知电池充入的电量E(单位:kW h)与充电时间t(单位:min)满足函数E(t)=M(1﹣e﹣kt),其中M表示电池的容量,k表示电池的充电效率.研究人员对A,B两个型号的电池进行充电测试,电池A的容量为80kW h,充电30min充入了40kW h的电量;电池B的容量为60kW h,充电15min充入了20kW h的电量.设电池A的充电效率为k1,电池B的充电效率为k2,则( )
A.k1>k2
B.k1<k2
C.k1=k2
D.k1,k2大小关系无法确定
2.折纸是我国民间的一种传统手工艺术.现有一张长10cm、宽8cm的长方形的纸片,将纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1,S2.若S1:S2=1:3,则折痕长的最大值为( )
A.cm B.10cm C.2cm D.2cm
3.某科技有限公司为了鼓励员工创新,打破发达国家的芯片垄断,计划逐年增加研发资金投入,若该公司2018年全年投入的研发资金为200万元,在此基础上,每年投入的研发资金比上一年增加10%,则该公司全年投入的研发资金开始超过400万元的年份是( )
(参考数据:1.16=1.77,1.17=1.95,1.18=2.14,1.19=2.36)
A.2024年 B.2025年 C.2026年 D.2027年
4.若某商店将进货单价为6元的商品按每件10元出售,则每天可销售100件,现准备采用提高售价、减少进货量的方法来增加利润.已知这种商品的售价每提高1元,销售量就要减少10件,那么要保证该商品每天的利润在450元以上,售价应定为( )
A.11元 B.11元到15元之间
C.15元 D.10元到14元之间
5.唐代诗人李顾的诗《古从军行》开头两句说“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为x2+y2≤1,若将军从点A(3,0)处出发,河岸线所在直线方程为x+y=4,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A. B.2 C. D.
6.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在地为点B(﹣2,3),若将军从点A(2,0)处出发,河岸线所在直线方程为x+y=3,则“将军饮马”的最短总路程为( )
A. B. C. D.
7.要测定古物的年代,可以用放射性碳法:在动植物的体内都含有微量的放射性14C,动植物死亡后,停止新陈代谢,14C不再产生,且原有的14C会自动衰变.经科学测定,14C的半衰期为5730(设14C的原始量为1,经过x年后,14C的含量f(x)=ax,即f(5730)=).现有一古物,测得14C为原始量的79.37%,则该古物距今约多少年?( )(参考数据:≈0.7937,≈0.9998)
A.1910 B.3581 C.9168 D.17190
8.Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为( )(参考数据ln19≈3)
A.60 B.62 C.66 D.63
9.有一组实验数据如表所示:
x 2.01 3 4.01 5.1 6.12
y 3 8.01 15 23.8 36.04
则最能体现这组数据关系的函数模型是( )
A.y=2x+1﹣1 B.y=x2﹣1 C.y=2log2x D.y=x3
10.已知函数f(x)=,在下列区间中,包含f(x)的零点的区间是( )
A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)
11.冈珀茨模型(y=ka)是由冈珀茨(Gompertz)提出,可作为动物种群数量变化的模型,并用于描述种群的消亡规律.已知某珍稀物种t年后的种群数量y近似满足冈珀茨模型:y=k0 e(当t=0时,表示2020年初的种群数量),若m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,则m的最小值为( )(ln2≈0.7)
A.5 B.6 C.7 D.8
12.某高校为加强学科建设,制定了第“十四五”(2021﹣2025)规划,计划逐年加大科研资金投入,已知该校计划2021年全年投入科研资金20万元,2025年全年投入科研资金28万元,则第“十四五”期间,投入科研资金的年均增长率约为( )
A.1.4﹣1 B.1.4﹣1 C.log1.45﹣1 D.log1.44﹣1
二.填空题(共4小题)
13.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量变为原来的一半所经历的时间称为它的半衰期,记为.现测得某种放射性元素的剩余质量A随时间t变化的6次数据如表:
t(单位时间) 0 2 4 6 8 10
A(t) 320 226 160 115 80 57
从以上记录可知这种元素的半衰期约为 个单位时间,剩余质量随时间变化的衰变公式为A(t)= .
14.为了参加校教职工运动会,某校高三年级组准备为本年级教师订制若干件文化衫,经与厂家协商,可按出厂价结算,同时厂家也承诺超过50件就可以每件比出厂价低22元给予优惠.如果按出厂价购买年级组总共应付a元,但若再多买15件就可以达到优惠条件并恰好也是共付a元(a为整数),则a的值为 .
15.某地在20年间经济高质量增长,GDP的值P(单位:亿元)与时间t(单位:年)之间的关系为P(t)=P(1+10%)t,其中P为t=0时的P值.假定P=2,那么在t=10时,GDP增长的速度大约是 .(单位:亿元/年,精确到0.01亿元/年)注:1.110≈2.59,当x取很小的正数时,ln(1+x)≈x.
16.根据国家统计局发布的第七次全国人口普查结果显示,截止2020年底,我国总人口数约为14亿,同2010年第六次全国人口普查数据相比,年平均增长率约为0.53%.若按此增长率,30年后我国人口总数约为 亿;为应对人口老龄化带来的挑战,改善我国人口结构,保持我国人力资源禀赋优势,党中央进一步优化了生育政策:若希望30年后,在中华人民共和国建国百年左右,我国人口超过20亿,那么人口年平均增长率应不低于 %.(精确到0.1)(参考数据:1.005330≈1.1718,100.005≈1.0116,lg7≈0.85)
三.解答题(共5小题)
17.筒车是我国古代发明的一种水利灌溉工具,因其经济环保,至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中描绘了筒车的工作原理,如图1是一个半径为R(单位:米),有24个盛水筒的筒车,按逆时针方向匀速旋转,转一周需要120秒,为了研究某个盛水筒P离水面高度h(单位:米)与时间t(单位:秒)的变化关系,建立如图2所示的平面直角坐标系xOy.已知t=0时P的初始位置为点A(2,﹣2)(此时P装满水).
(1)P从出发到开始倒水入槽需要用时40秒,求此刻P距离水面的高度(结果精确到0.1);
(2)记与P相邻的下一个盛水筒为Q,在筒车旋转一周的过程中,求P与Q距离水面高度差的最大值(结果精确到0.1).
18.有四个小镇恰好位于边长为10千米的菱形ABCD的四个顶点处.政府拟建公路连通四个小镇,若每千米公路的建设成本是10万元,预算为280万元,原计划按照菱形ABCD对角线修路.
(1)若预算刚好花完,求菱形ABCD的面积;
(2)若ABCD为正方形,施工队发现按照原计划修路会预算不足,于是采取如下新方案:按如图实线所示修路,其中AM=BM=CN=DN,∠BAM=θ,θ∈(0,),问:新方案能否在预算内完成修路目标?求出新方案的最低花费.
19.已知有半径为1,圆心角为α(其中α为给定的锐角)的扇形铁皮OMN,现利用这块铁皮并根据下列方案之一,裁剪出一个矩形.
方案1:如图1,裁剪出的矩形ABCD的顶点A,B在线段ON上,点C在弧上,点D在线段OM上;
方案2:如图2,裁剪出的矩形PQRS的顶点P,S分别在线段OM,ON上,顶点Q,R在弧上,并且满足PQ∥RS∥OE,其中点E为弧的中点.
(1)按照方案1裁剪,设∠NOC=θ,用θ表示矩形ABCD的面积S1,并证明S1的最大值为tan;
(2)按照方案2裁剪,求矩形PQRS的面积S2的最大值,并与(1)中的结果比较后指出按哪种方案可以裁剪出面积最大的矩形.
20.了解某些细菌、病毒的生存条件、繁殖习性等对于预防疾病的传播、保护环境有极其要的意义.某科研团队在培养基中放入一定量某种细菌进行研究,发现其蔓延速度越来越快,经过2分钟菌落的覆盖面积为18mm2,经过3分钟覆盖面积为27mm2,现菌落覆盖面积y(单位:mm2)与经过时间x(单位:min)的关系有两个函数模型y=kax(k>0,a>1)与y=p+q(p>0)可供选择.(参考数据:36=729,37=2187,38=6561,39=19683,≈1.414,≈1.732.)
(1)试判断哪个函数模型更合适,说明理由,并求出该模型的解析式;
(2)在理想状态下,至少经过多久培养基中菌落面积能超过200mm2?(计算结果保留到整数)
21.某企业采用新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=﹣200x+80000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
专题练习《函数应用》
参考答案与试题解析
一.选择题(共12小题)
1.充电电池是电动汽车的核心部件之一,如何提高充电速度是电池制造商重点关注的研究方向.已知电池充入的电量E(单位:kW h)与充电时间t(单位:min)满足函数E(t)=M(1﹣e﹣kt),其中M表示电池的容量,k表示电池的充电效率.研究人员对A,B两个型号的电池进行充电测试,电池A的容量为80kW h,充电30min充入了40kW h的电量;电池B的容量为60kW h,充电15min充入了20kW h的电量.设电池A的充电效率为k1,电池B的充电效率为k2,则( )
A.k1>k2
B.k1<k2
C.k1=k2
D.k1,k2大小关系无法确定
【考点】根据实际问题选择函数类型.【专题】计算题;方程思想;综合法;函数的性质及应用;逻辑推理;数学运算.
【分析】列出方程后比较k1,k2大小.
【解答】解:由题意得,则,
同理,则,得,
由指数函数单调性得﹣30k2<﹣30k1,即k1<k2.
故选:B.
【点评】本题主要考查函数模型及其应用,属于基础题.
2.折纸是我国民间的一种传统手工艺术.现有一张长10cm、宽8cm的长方形的纸片,将纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1,S2.若S1:S2=1:3,则折痕长的最大值为( )
A.cm B.10cm C.2cm D.2cm
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;分析法;函数的性质及应用;数学运算.
【分析】由已知可确定,分别在三种折叠方式下利用面积建立关于折痕的函数关系式,根据二次函数和对勾函数的单调性可求得最值,由此可得结果.
【解答】解:由题意得:长方形纸片的面积为 10×8=80(cm2),又 S1:S2=1:3,
∴,
①当折痕如下图所示时,
设AM=x,AN=y,则,解得:,∴,
②当折痕如下图所示时,
设AN=x,DM=y,则 ,解得:,
∵f(t) 在 (25,40)上单调递减,在 (40,100)上单调递增,
又 ,∴g(x)∈[64,89],
∴,
③当折痕如下图所示时,
设AF=x,BE=y,则 ,解得:,
∴EF2=(x﹣y)2+100=(2x﹣4)2+100,
令h(x)=(2x﹣4)2+100(0≤x≤4),则h(x)在(0,2)上单调递减,在(2,4)上单调递增,
又h(0)=16+100=116,h(2)=100,h(4)=16+100=116,∴h(x)∈[100,116],
∴;
综上所述:折痕长的取值范围为;
∴折痕长的最大值为.
故选:C.
【点评】本题考查函数的实际应用,考查学生的运算能力,属于中档题.
3.某科技有限公司为了鼓励员工创新,打破发达国家的芯片垄断,计划逐年增加研发资金投入,若该公司2018年全年投入的研发资金为200万元,在此基础上,每年投入的研发资金比上一年增加10%,则该公司全年投入的研发资金开始超过400万元的年份是( )
(参考数据:1.16=1.77,1.17=1.95,1.18=2.14,1.19=2.36)
A.2024年 B.2025年 C.2026年 D.2027年
【考点】根据实际问题选择函数类型.【专题】函数思想;数学模型法;函数的性质及应用;逻辑推理.
【分析】设第n年开始400万元,由题意,列出关于n的不等式,求解即可.
【解答】解:设第n年开始超过400万元,
则200×(1+10%)n﹣2018>400,即1.1n﹣2018>2,
因为1.17=1.95,1.18=2.14,
所以当n﹣2018=8,即n=2026时,该公司全年投入的研发资金开始超过400万元.
故选:C.
【点评】本题考查了函数模型的选择与应用,解题的关键是建立符合条件的函数模型,分析清楚问题的逻辑关系是解题的关键,此类问题求解的一般步骤是:建立函数模型,进行函数计算,得出结果,再将结果反馈到实际问题中指导解决问题,考查了逻辑推理能力与化简运算能力,属于中档题.
4.若某商店将进货单价为6元的商品按每件10元出售,则每天可销售100件,现准备采用提高售价、减少进货量的方法来增加利润.已知这种商品的售价每提高1元,销售量就要减少10件,那么要保证该商品每天的利润在450元以上,售价应定为( )
A.11元 B.11元到15元之间
C.15元 D.10元到14元之间
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;分析法;函数的性质及应用;数学运算.
【分析】由题意列出关于利润的解析式,再求利润在450元以上的x的范围.
【解答】解:设每件商品的售价提高x(0<x<10)元,
则每件获得利润(4+x)元,每天可销售(100﹣10x)件.
设该商品每天的利润为y元,则
由题意有y=(4+x)(100﹣10x)=﹣10x2+60x+400,
要保证每天的利润在450元以上,
则﹣10x2+60x+400>450,x ﹣6+5<0,
得1<x<5,
故每件商品的售价在11元到15元之间时,能确保该商品每天的利润在450元以上.
故选:B.
【点评】本题考查函数在实际生活中的应用,属于中档题.
5.唐代诗人李顾的诗《古从军行》开头两句说“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为x2+y2≤1,若将军从点A(3,0)处出发,河岸线所在直线方程为x+y=4,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A. B.2 C. D.
【考点】根据实际问题选择函数类型;与直线关于点、直线对称的直线方程.
【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】设点A关于直线x+y=4的对称性A'(a,b),军营所在区域的圆心为C,则A'C﹣1为最短总路程,再结合A与A’关于直线x+y=4对称,求出A'的坐标,再结合两点之间的距离公式,即可求解.
【解答】解:设点A关于直线x+y=4的对称性A'(a,b),军营所在区域的圆心为C,
则A'C﹣1为最短总路程,
AA'的中点为(),直线AA'的斜率为1,
故直线AA'为y=x﹣3,
由,解得a=4,b=1,
所以A'C=,即A'C=.
故选:D.
【点评】本题主要考查函数的实际应用,考查计算能力,属于中档题.
6.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在地为点B(﹣2,3),若将军从点A(2,0)处出发,河岸线所在直线方程为x+y=3,则“将军饮马”的最短总路程为( )
A. B. C. D.
【考点】根据实际问题选择函数类型.【专题】转化思想;转化法;直线与圆;逻辑推理;数学运算.
【分析】利用点关于点的对称点的求法,求出点A关于直线x+y=3的对称点A',由三点共线取得最小值,结合两点间距离公式求解即可.
【解答】解:由题意可知,点A(2,0),
则点A(2,0)关于直线x+y=3的对称点为A'(a,b),
则,解得a=3,b=1,
故A'(3,1),
又军营所在地为点B(﹣2,3),
所以“将军饮马”的最短总路程为|A'B|=.
故选:C.
【点评】本题考查了直线在实际生活中的应用,点关于直线的对称点的求解,两点间斜率公式以及两点间距离公式的应用,两条直线垂直的充要条件的运用,考查了逻辑推理能力与化简运算能力,属于中档题.
7.要测定古物的年代,可以用放射性碳法:在动植物的体内都含有微量的放射性14C,动植物死亡后,停止新陈代谢,14C不再产生,且原有的14C会自动衰变.经科学测定,14C的半衰期为5730(设14C的原始量为1,经过x年后,14C的含量f(x)=ax,即f(5730)=).现有一古物,测得14C为原始量的79.37%,则该古物距今约多少年?( )(参考数据:≈0.7937,≈0.9998)
A.1910 B.3581 C.9168 D.17190
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;综合法;函数的性质及应用;数学运算.
【分析】由f(5730)=可得,令f(x)=0.7937,得x=loga0.7937,利用换底公式结合对数的运算性质即可求出x的值.
【解答】解:设14C的原始量为1,经过x年后,14C的含量f(x)=ax,
由题意可知:f(5730)=,即,
∴,
令f(x)=0.7937,得:ax=0.7937,
∴x=loga0.7937=====1910,
∴该古物距今约1910年.
故选:A.
【点评】本题主要考查了函数的实际应用,考查了对数的运算,是中档题.
8.Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为( )(参考数据ln19≈3)
A.60 B.62 C.66 D.63
【考点】根据实际问题选择函数类型.【专题】函数思想;数学模型法;函数的性质及应用;数学建模.
【分析】根据所给材料的公式列出方程=0.95K,解出t即可.
【解答】解:由已知可得=0.95K,解得e﹣0.23(t*﹣50)=,
两边取对数有﹣0.23(t*﹣50)=﹣ln19,
解得t*≈63,
故选:D.
【点评】本题考查函数模型的实际应用,考查学生计算能力,是基础题.
9.有一组实验数据如表所示:
x 2.01 3 4.01 5.1 6.12
y 3 8.01 15 23.8 36.04
则最能体现这组数据关系的函数模型是( )
A.y=2x+1﹣1 B.y=x2﹣1 C.y=2log2x D.y=x3
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;方程思想;转化思想;函数的性质及应用.
【分析】利用函数的表格关系判断函数的解析式的可能性,然后验证求解即可.
【解答】解:由函数的表格可知,函数的解析式应该是指数函数类型与二次函数的类型,选项C不正确;
当x=2.01时,y=2x+1﹣1>4;y=x2﹣1≈3,y=x3>7,
当x=3时,y=2x+1﹣1=15;y=x2﹣1≈8,y=x3=27,
故选:B.
【点评】本题考查函数的解析式的判断与应用,函数的模型的应用,是基础题.
10.已知函数f(x)=,在下列区间中,包含f(x)的零点的区间是( )
A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)
【考点】二分法的定义与应用.【专题】计算题;函数思想;定义法;函数的性质及应用.
【分析】函数f(x)在其定义域上连续,同时可判断f(4)<0,f(2)>0;从而判断.
【解答】解:函数f(x)=f(x)=,在其定义域上连续,
f(4)=﹣2<0,
f(2)=3﹣1>0;
故函数f(x)的零点在区间(2,4)上,
故选:C.
【点评】本题考查了函数的零点的判断与应用,属于基础题.
11.冈珀茨模型(y=ka)是由冈珀茨(Gompertz)提出,可作为动物种群数量变化的模型,并用于描述种群的消亡规律.已知某珍稀物种t年后的种群数量y近似满足冈珀茨模型:y=k0 e(当t=0时,表示2020年初的种群数量),若m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,则m的最小值为( )(ln2≈0.7)
A.5 B.6 C.7 D.8
【考点】根据实际问题选择函数类型;对数的运算性质
转化思想;转化法;函数的性质及应用;数学运算.
【分析】由已知条件可得,当t=0时,y=,当t=m时,y=,由m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,可得<,再结合对数函数的公式,即可求解.
【解答】解:∵y=k0 e,
当t=0时,y=,
∴当t=m时,y=,
∵m(m∈N)年后,该物种的种群数量将不足2020年初种群数量的一半,
∴<,
由题可知,k0 是大于0的常数,即2 ,两边取对数可得,ln2+1.4e﹣0.125m<1.4,
∵ln2≈0.7,
∴,两边取对数可得,﹣0.125m<﹣ln2≈﹣0.7,解得m>5.6,m∈N*,
故m的最小值为6.
故选:B.
【点评】本题主要考查函数的实际应用,掌握对数函数的公式是解本题的关键,属于中档题.
12.某高校为加强学科建设,制定了第“十四五”(2021﹣2025)规划,计划逐年加大科研资金投入,已知该校计划2021年全年投入科研资金20万元,2025年全年投入科研资金28万元,则第“十四五”期间,投入科研资金的年均增长率约为( )
A.1.4﹣1 B.1.4﹣1 C.log1.45﹣1 D.log1.44﹣1
【考点】根据实际问题选择函数类型;指数函数的图象与性质.【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】设年增长率为x,由题意可得,20(1+x)4=28,解出x的取值范围,即可求解.
【解答】解:设年增长率为x,由题意可得,20(1+x)4=28,即,
所以,解得x=,
故投入科研资金的年均增长率约为.
故选:A.
【点评】本题主要考查函数的实际应用,掌握指数函数的公式是解本题的关键,属于基础题.
二.填空题(共4小题)
13.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量变为原来的一半所经历的时间称为它的半衰期,记为.现测得某种放射性元素的剩余质量A随时间t变化的6次数据如表:
t(单位时间) 0 2 4 6 8 10
A(t) 320 226 160 115 80 57
从以上记录可知这种元素的半衰期约为 4 个单位时间,剩余质量随时间变化的衰变公式为A(t)= (t≥0) .
【考点】根据实际问题选择函数类型.【专题】转化思想;分析法;函数的性质及应用;数学运算.
【分析】首先观察表格,根据半衰期的定义,可得半衰期为4个单元时间,初始质量为A(0)=320,根据题意可知此模型是指数函数模型,且底数为,指数为经过的时间除以半衰期,结合初始质量,即可求解.
【解答】解:从题表中数据易知半衰期为4个单位时间,由初始质量为A0=320,则经过时间t的剩余质量为A(t)==(t≥0).
(t≥0).
故答案为:4,(t≥0).
【点评】本题考查了函数模型的实际应用,关键是理解半衰期的定义,属于基础题.
14.为了参加校教职工运动会,某校高三年级组准备为本年级教师订制若干件文化衫,经与厂家协商,可按出厂价结算,同时厂家也承诺超过50件就可以每件比出厂价低22元给予优惠.如果按出厂价购买年级组总共应付a元,但若再多买15件就可以达到优惠条件并恰好也是共付a元(a为整数),则a的值为 3960 .
【考点】根据实际问题选择函数类型.【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】设按出厂价购买x(x≤50)套,应付a元,出厂价为y元,则有a=xy (x≤50)①,再多买15套,就可以按优惠价结算恰好也付a元,则有a=(x+15)(y﹣22)(x+15>50)②,联立①②,再结合x,a为整数,即可求解.
【解答】解:设按出厂价购买x(x≤50)套,应付a元,出厂价为y元,
则有a=xy (x≤50)①,
再多买15套,就可以按优惠价结算恰好也付a元,
则有a=(x+15)(y﹣22)(x+15>50)②,
联立①②可得,xy=xy+15y﹣22x﹣330,即y=(35<x≤50),
∵x为整数,a为整数,
∴x=45,y=88,
故a=xy=45×88=3960.
故答案为:3960.
【点评】本题主要考查函数的实际应用,考查计算能力,属于基础题.
15.某地在20年间经济高质量增长,GDP的值P(单位:亿元)与时间t(单位:年)之间的关系为P(t)=P(1+10%)t,其中P为t=0时的P值.假定P=2,那么在t=10时,GDP增长的速度大约是 0.52 .(单位:亿元/年,精确到0.01亿元/年)注:1.110≈2.59,当x取很小的正数时,ln(1+x)≈x.
【考点】根据实际问题选择函数类型.【专题】计算题;方程思想;综合法;函数的性质及应用;逻辑推理;数学运算.
【分析】由题可得GDP增长的速度为P'(t)=2×1.1tln1.1,进而即得.
【解答】解:由题可知P(t)=2(1+10%)t=2×1.1t,
所以P'(t)=2×1.1tln1.1,
所以P'(10)=2×1.110ln1.1≈2×2.59×0.1=0.518≈0.52,
即GDP增长的速度大约是0.52.
故答案为:0.52.
【点评】本题主要考查函数模型及其应用,对数及其近似运算等知识,属于基础题.
16.根据国家统计局发布的第七次全国人口普查结果显示,截止2020年底,我国总人口数约为14亿,同2010年第六次全国人口普查数据相比,年平均增长率约为0.53%.若按此增长率,30年后我国人口总数约为 16.4 亿;为应对人口老龄化带来的挑战,改善我国人口结构,保持我国人力资源禀赋优势,党中央进一步优化了生育政策:若希望30年后,在中华人民共和国建国百年左右,我国人口超过20亿,那么人口年平均增长率应不低于 1.2 %.(精确到0.1)(参考数据:1.005330≈1.1718,100.005≈1.0116,lg7≈0.85)
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;定义法;函数的性质及应用;数学建模;数学运算.
【分析】根据年平均增长率约为0.53%求解;设年平均增长率为p,由14(1+p)30>20求解
【解答】解:因为2020年底,我国总人口数约为14亿,且年平均增长率约为0.53%,
所以30年后我国人口总数约为 14(1+0.53%)30=14×1.005330≈14×1.1718=16.4;
设年平均增长率为 p,
由题意得:14(1+p)30>20,
则 ,
两边取对数得 30lg(1+p)>1﹣lg7≈0.15,
即lg(1+p)>0.005,
所以 1+p>100.005≈1.0116,
解得 p>0.0116,
所以人口年平均增长率应不低于 1.2%,
故答案为:16.4,1.2.
【点评】本题考查指数运算,考查指数方程的解法,考查数学建模和数学运算的核心素养,属于基础题.
三.解答题(共5小题)
17.筒车是我国古代发明的一种水利灌溉工具,因其经济环保,至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中描绘了筒车的工作原理,如图1是一个半径为R(单位:米),有24个盛水筒的筒车,按逆时针方向匀速旋转,转一周需要120秒,为了研究某个盛水筒P离水面高度h(单位:米)与时间t(单位:秒)的变化关系,建立如图2所示的平面直角坐标系xOy.已知t=0时P的初始位置为点A(2,﹣2)(此时P装满水).
(1)P从出发到开始倒水入槽需要用时40秒,求此刻P距离水面的高度(结果精确到0.1);
(2)记与P相邻的下一个盛水筒为Q,在筒车旋转一周的过程中,求P与Q距离水面高度差的最大值(结果精确到0.1).
【考点】根据实际问题选择函数类型;三角函数模型的应用.【专题】转化思想;转化法;函数的性质及应用;数学运算.
【分析】(1)根据已知条件,先求出线段OA按逆时针方向旋转了,再结合A点的坐标,即可求解.
(2)根据已知条件,分别求出P开始转动t秒后距离水面的高度h1,Q距离水面的高度h2,则P,Q距离水面的高度差H=|h1﹣h2|,再结合三角函数的恒等变换,即可求解.
【解答】解:(1)由于筒车转一周需要120秒,
所以P从出发到开始倒水入槽的40秒,线段OA按逆时针方向旋转了,
因为A点坐标为(2,﹣2),则,以OA为终边的角为,
所以P距离水面的高度为≈6.9m.
(2)由于筒车转一周需要120秒,可知P转动的角度为,
又以OA为终边的角为,
则P开始转动t秒后距离水面的高度,0≤t≤120,
如图所示,
P,Q两个盛水筒分别用点B,C表示,
则,点C相对于点B始终落后rad,
此时Q距离水面的高度,
则P,Q距离水面的高度差H=|h1﹣h2|==,0≤t≤120,
利用sinθ+sinφ=,可得H=,
当或,解得t=22.5或t=82.5,
故H最大值为,
所以P与Q距离水面高度差的最大值约为1.0m.
【点评】本题主要考查函数的实际应用,考查转化能力,属于难题.
18.有四个小镇恰好位于边长为10千米的菱形ABCD的四个顶点处.政府拟建公路连通四个小镇,若每千米公路的建设成本是10万元,预算为280万元,原计划按照菱形ABCD对角线修路.
(1)若预算刚好花完,求菱形ABCD的面积;
(2)若ABCD为正方形,施工队发现按照原计划修路会预算不足,于是采取如下新方案:按如图实线所示修路,其中AM=BM=CN=DN,∠BAM=θ,θ∈(0,),问:新方案能否在预算内完成修路目标?求出新方案的最低花费.
【考点】根据实际问题选择函数类型.【专题】应用题;函数思想;构造法;三角函数的求值;数学运算.
【分析】(1)设菱形对角线分别为x,y,根据题意求出x、y的关系,再计算菱形ABCD的面积.
(2)延长MN、NM,交AB、CD于点F、G,求出AM+BM+CN+DN+MN的表达式,再构造函数,利用函数求出函数的最小值,即可得出结论.
【解答】解:(1)设菱形对角线分别为x,y,依题意知,x+y==28,
又因为菱形的对角线互相垂直且平分,所以+=102,即x2+y2=400,
所以(x+y)2﹣2xy=400,解得xy=192,
所以菱形ABCD的面积为xy=×192=96(平方米).
(2)
延长MN、NM,交AB、CD于点F、G,如图所示:
因为AM=BM=CN=DN,∠BAM=θ,
所以=cosθ,解得AM=,
所以AM+BM+CN+DN=,
又因为=tanθ=,解得FM=,所以MN=10﹣,
因此总长度为10+10×,
设f(θ)=,θ∈(0,),则f′(θ)=,
当θ∈(0,)时,f′(θ)<0,f(θ)单调递减,
当θ∈(,),f′(θ)>0,f(θ)单调递增;
当θ=时,f(θ)=0,f(θ)取得最小值为f()==,
此时总长度最小,为10+10,对应的总费用为(10+10)×10=100+100<280,
所以新方案能在预算内完成修路目标,且新方案的最低花费为(100+100)万元.
【点评】本题考查了三角函数求值的应用问题,也考查了利用函数求最值问题,是中档题.
19.已知有半径为1,圆心角为α(其中α为给定的锐角)的扇形铁皮OMN,现利用这块铁皮并根据下列方案之一,裁剪出一个矩形.
方案1:如图1,裁剪出的矩形ABCD的顶点A,B在线段ON上,点C在弧上,点D在线段OM上;
方案2:如图2,裁剪出的矩形PQRS的顶点P,S分别在线段OM,ON上,顶点Q,R在弧上,并且满足PQ∥RS∥OE,其中点E为弧的中点.
(1)按照方案1裁剪,设∠NOC=θ,用θ表示矩形ABCD的面积S1,并证明S1的最大值为tan;
(2)按照方案2裁剪,求矩形PQRS的面积S2的最大值,并与(1)中的结果比较后指出按哪种方案可以裁剪出面积最大的矩形.
【考点】根据实际问题选择函数类型.【专题】整体思想;综合法;函数的性质及应用;数学运算.
【分析】(1)分别用含有θ的三角函数表示AD,AB,写出矩形面积,利用三角函数求解最值即可;(2)在图2中,设OE与PS,QR分别交于G,H,则利用(1)的结论,可以得到矩形PQHG的最大面积为,根据对称性,矩形PQRS的最大面积为tan,然后利用作差法比较大小即可.
【解答】解:(1)在图1中,r=1,∠NOC=θ,θ∈(0,α),
AD=BC=rsinθ=sinθ,OB=rcosθ=cosθ,AB=OB﹣OA=OB﹣=cos,
S1=SABCD=sin=(sin2θ﹣)=(sin2)﹣
=﹣=,
当θ=时,矩形ABCD的最大面积为=,
故原结论成立;
(2)在图(2)中,设OE与边PS,QR分别交于点G,H,
则利用(1)的结论,可以得到矩形PQHG的最大面积为,
根据对称性,矩形PQRS的最大面积为tan,
因为α为锐角,所以,
于是0,
因此,=>0,
故按照方案1可以裁剪出面积最大的矩形,其最大面积为.
【点评】本题考查了函数模型的选择以及应用,考查了三角函数的运算以及学生的运算求解能力,属于中档题.
20.2020年,全世界范围内都受到“新冠”疫情的影响.了解某些细菌、病毒的生存条件、繁殖习性等对于预防疾病的传播、保护环境有极其要的意义.某科研团队在培养基中放入一定量某种细菌进行研究,发现其蔓延速度越来越快,经过2分钟菌落的覆盖面积为18mm2,经过3分钟覆盖面积为27mm2,现菌落覆盖面积y(单位:mm2)与经过时间x(单位:min)的关系有两个函数模型y=kax(k>0,a>1)与y=p+q(p>0)可供选择.(参考数据:36=729,37=2187,38=6561,39=19683,≈1.414,≈1.732.)
(1)试判断哪个函数模型更合适,说明理由,并求出该模型的解析式;
(2)在理想状态下,至少经过多久培养基中菌落面积能超过200mm2?(计算结果保留到整数)
【考点】根据实际问题选择函数类型.【专题】计算题;函数思想;分析法;函数的性质及应用;数学运算.
【分析】(1)根据函数的单调性可知选哪个模型更合适;
(2)解指数函数不等式可求得答案
【解答】解:(1)y=kax(k>0,a>1)的增长速度越来越快,y=p+q(p>0)的增长速度越来越慢,
根据题意应选y=kax(k>0,a>l),
于是,解得:,
∴y=8()x(x∈N),
(2)根据y=8()x(x∈N)函数模型,可得不等式8()x>200,解得x≥8,
故至少经过8min 培养基中菌落面积能超过200mm2.
【点评】本题考查指数函数模型及其应用,考查了学生的运算能力,属于中档题.
21.某企业采用新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=﹣200x+80000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
【考点】根据实际问题选择函数类型.【专题】函数思想;数学模型法;函数的性质及应用;数学建模.
【分析】(1)由题意列出该单位每月处理量的函数表达式,利用基本不等式求最值;
(2)写出该单位没有的获利f(x)关于x的函数,整理后利用二次函数的单调性求最值,则答案可求.
【解答】解:(1)由题意可知:,
所以,每吨二氧化碳的平均处理成本为,
由基本不等式可得:(元),
当且仅当时,即当x=400时,等号成立,
因此,该单位每月处理量为400吨时,才能使每吨的平均处理成本最低.
(2)令f(x)=100x﹣
=﹣x2+300x﹣80000=,
∵300≤x≤600,函数f(x)在区间[300,600]上单调递减,
∴当x=300时,函数f(x)取得最大值,即f(x)max=f(300)=﹣35000.
所以,该单位每月不能获利,国家至少需要补贴35000元才能使该单位不亏损.
【点评】本题考查函数模型的选择及应用,考查利用基本不等式与配方法求最值。
考点卡片
1.指数函数的图象与性质
【知识点的认识】
1、指数函数y=ax(a>0,且a≠1)的图象和性质:
y=ax a>1 0<a<1
图象
定义域 R
值域 (0,+∞)
性质 过定点(0,1)
当x>0时,y>1;x<0时,0<y<1 当x>0时,0<y<1;x<0时,y>1
在R上是增函数 在R上是减函数
2、底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.
③当a>0,且a≠l时,函数y=ax 与函数y=的图象关于y轴对称.
3、利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值.
2.对数的运算性质
【知识点的认识】
对数的性质:①=N;②logaaN=N(a>0且a≠1).
loga(MN)=logaM+logaN; loga=logaM﹣logaN;
logaMn=nlogaM; loga=logaM.
3.二分法的定义与应用
【二分法的定义】
二分法 即一分为二的方法.设函数f(x)在[a,b]上连续,且满足f(a) f(b)<0,我们假设f(a)<0,f(b)>0,那么当x1=时,若f(x1)=0,这说x1为零点;若不为0,假设大于0,那么继续在[x1,b]区间取中点验证它的函数值为0,一直重复下去,直到找到满足要求的点为止.这就是二分法的基本概念.
【二分法的应用】
我们以具体的例子来说说二分法应用的一个基本条件:
例题:下列函数图象均与x轴有交点,其中能用二分法求函数零点的是
解:能用二分法求函数零点的函数,在零点的左右两侧的函数值符号相反,
有图象可得,只有③能满足此条件,
故答案为 ③.
在这个例题当中,所要求的能力其实就是对概念的理解,这也是二分法它惯用的考查形式,通过这个例题,希望同学们能清楚二分法的概念和常考题型.
【二分法求方程的近似解】
二分法在高中主要属于了解性的内容,拿二分法求近似解思路也比较固定,这里我们主要以例题来做讲解.
例:用二分法求方程在[1,2]上的近似解,取中点c=1.5,则下一个有根区间是 [1.5,2] .
解:令函数f(x)=lnx﹣,由于f(1.5)=ln(1.5)﹣=(ln1.52﹣2)<(lne2﹣2)=0,即f(1.5)<0,
而f(2)=ln2﹣=ln2﹣ln=ln=ln>ln1=0,即f(2)>0,
故函数f(x)在[1.5 2]上存在零点,故方程在[1.5,2]上有根,
故答案为[1.5,2].
通过这个例题,我们可以发现二分法的步奏,第一先确定f(a) f(b)<0的a,b点;第二,寻找区间(a,b)的中点,并判断它的函数值是否为0;第三,若不为0,转第一步.
4.根据实际问题选择函数类型
【知识点的知识】
1.实际问题的函数刻画
在现实世界里,事物之间存在着广泛的联系,许多联系可以用函数刻画.用函数的观点看实际问题,是学习函数的重要内容.
2.用函数模型解决实际问题
(1)数据拟合:
通过一些数据寻求事物规律,往往是通过绘出这些数据在直角坐标系中的点,观察这些点的整体特征,看它们接近我们熟悉的哪一种函数图象,选定函数形式后,将一些数据代入这个函数的一般表达式,求出具体的函数表达式,再做必要的检验,基本符合实际,就可以确定这个函数基本反映了事物规律,这种方法称为数据拟合.
(2)常用到的五种函数模型:
①直线模型:一次函数模型y=kx+b(k≠0),图象增长特点是直线式上升(x的系数k>0),通过图象可以直观地认识它,特例是正比例函数模型y=kx(k>0).
②反比例函数模型:y=(k>0)型,增长特点是y随x的增大而减小.
③指数函数模型:y=a bx+c(b>0,且b≠1,a≠0),其增长特点是随着自变量的增大,函数值增大的速度越来越快(底数b>1,a>0),常形象地称为指数爆炸.
④对数函数模型,即y=mlogax+n(a>0,a≠1,m≠0)型,增长特点是随着自变量的增大,函数值增大越来越慢(底数a>1,m>0).
⑤幂函数模型,即y=a xn+b(a≠0)型,其中最常见的是二次函数模型:y=ax2+bx+c(a≠0),其特点是随着自变量的增大,函数值先减小后增大(a>0).
在以上几种函数模型的选择与建立时,要注意函数图象的直观运用,分析图象特点,分析变量x的范围,同时还要与实际问题结合,如取整等.
3.函数建模
(1)定义:用数学思想、方法、知识解决实际问题的过程,叫作数学建模.
(2)过程:如下图所示.
【典型例题分析】
典例1:某公司为了实现1000万元的利润目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的25%,其中模型能符合公司的要求的是(参考数据:1.003600≈6,1n7≈1.945,1n102≈2.302)( )
A.y=0.025x B.y=1.003xC.y=l+log7x D.y=x2
分析:由题意,符合公司要求的模型只需满足:当x∈[10,1000]时,①函数为增函数;②函数的最大值不超过5;③y≤x 25%,然后一一验证即可.
解答:解:由题意,符合公司要求的模型只需满足:
当x∈[10,1000]时,
①函数为增函数;②函数的最大值不超过5;③y≤x 25%=x,
A中,函数y=0.025x,易知满足①,但当x>200时,y>5不满足公司要求;
B中,函数y=1.003x,易知满足①,但当x>600时,y>5不满足公司要求;
C中,函数y=l+log7x,易知满足①,当x=1000时,y取最大值l+log71000=4﹣lg7<5,且l+log7x≤x恒成立,故满足公司要求;
D中,函数y=x2,易知满足①,当x=400时,y>5不满足公司要求;
故选C
点评:本题以实际问题为载体,考查函数模型的构建,考查方案的优化设计,解题的关键是一一验证.
典例2:某服装生产企业为了占有更多的市场份额,拟在2015年度进行一系列促销活动,经过市场调查和测算,服装的年销量x万件与年促销t万元之间满足关系式3﹣x=(k为常数),如果不搞促销活动,服装的年销量只能是1万件.已知2015年生产服装的设备折旧,维修等固定费用需要3万元,每生产1万件服装需再投入32万元的生产费用,若将每件服装的售价定为:“每件生产成本的150%”与“平均每件促销费的一半”之和,试求:
(1)2015年的利润y(万元)关于促销费t (万元)的函数;
(2)该企业2015年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入﹣生产成本﹣促销费,生产成本=固定费用+生产费用)
分析:(1)通过x表示出年利润y,并化简整理,代入整理即可求出y万元表示为促销费t万元的函数.
(2)根据已知代入(2)的函数,分别进行化简即可用基本不等式求出最值,即促销费投入多少万元时,企业的年利润最大.
解答:解:(1)由题意:3﹣x=,
且当t=0时,x=1.
所以k=2,所以3﹣x=,…(1分)
生产成本为 32x+3,每件售价,…(2分)
所以,y=…(3分)
=16x﹣=,(t≥50);…(2分)
(2)因为 当且仅当,即t=7时取等号,…(4分)
所以y≤50﹣8=42,…(1分)
答:促销费投入7万元时,企业的年利润最大.…(1分)
点评:本小题主要考查函数模型的选择与应用,看出基本不等式在求最值中的应用,考查学生分析问题和解决问题的能力,强调对知识的理解和熟练运用,考查转化思想的应用.
【解题方法点拨】
用函数模型解决实际问题的常见类型及解法:
(1)解函数关系已知的应用题
①确定函数关系式y=f(x)中的参数,求出具体的函数解析式y=f(x);②讨论x与y的对应关系,针对具体的函数去讨论与题目有关的问题;③给出实际问题的解,即根据在函数关系的讨论中所获得的理论参数值给出答案.
(2)解函数关系未知的应用题
①阅读理解题意
看一看可以用什么样的函数模型,初步拟定函数类型;
②抽象函数模型
在理解问题的基础上,把实际问题抽象为函数模型;
③研究函数模型的性质
根据函数模型,结合题目的要求,讨论函数模型的有关性质,获得函数模型的解;
④得出问题的结论
根据函数模型的解,结合实际问题的实际意义和题目的要求,给出实际问题的解.
5.三角函数模型的应用
【知识点的知识】
1. 三角函数模型的简单应用:1)在生活中的应用;2);在建筑学中的应用;3)在航海中的应用;4)在物理学中的应用.
2. 解三角函数应用题的一般步骤:
(1)阅读理解材料:将文字语言转化为符号语言;
(2)建立变量关系:抽象成数学问题,建立变量关系;
(3)讨论变量性质:根据函数性质讨论变量性质;
(4)作出结论.
【解题方法点拨】
1、方法与技巧:
(1)在生产生活中,常常有一些与角有关的最值问题,需要确定以角作为变量的三角函数来解决.
(2)理清题意,分清题目中已知和所求,准确解读题目中的术语和有关名词.
(3)要能根据题意,画出符合题意的图形.
(4)对计算结果,可根据实际情况进行处理.
2、注意:
(1)建立三角函数关系式关键是选择适当的角作为变量.
(2)解决应用问题要注重检验.
(3)选择变量后,要根据题中的条件,确定角的范围.
6.与直线关于点、直线对称的直线方程
【知识点的知识】
点与直线的对称问题:
(l)点关于点对称(中点坐标公式):
点关于点成中心对称的对称中心恰是以这两点为端点的线段的中点,因此中心对称的问题是线段中点坐标公式的应用问题.设P(x0,y0),对称中心为A(a,b),则P关于A的对称点为P′(2a﹣x0,2b﹣y0)
(2)点关于直线成轴对称问题
由轴对称定义知,对称轴即为两对称点连线的“垂直平分线”.利用“垂直”“平分”这两个条件建立方程组,就可求出对称点的坐标.一般情形如下:
设点P(x0,y0),关于直线y=kx+b的对称点为P′(x′,y′),则有
可求出x′,y′.
特殊地,点P(x0,y0)关于直线x=a的对称点为P′(2a﹣x0,y0);点P(x0,y0)关于直线y=b的对称点为P′(x0,2b﹣y0).
(3)线关于点对称(转化为点关于点对称,或代入法,两条直线平行):
(4)线关于线对称(求交点,转化为点关于线对称):
由平面几何知识可知若直线a、b关于直线l对称,它们具有下列几何性质:
①若a、b相交,则l是a、b交角的平分线;
②若点A在直线a上,那么A关于直线l的对称点B一定在直线b上,这时AB⊥l,并且AB的中点D在l上;
③a以l为轴旋转180°,一定与b重合.
第1页(共1页)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
