24.1.4圆周角同步练习(无答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1.4圆周角同步练习(无答案)2023-2024学年人教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览



文档简介
24.1.4圆周角
一、选择题。
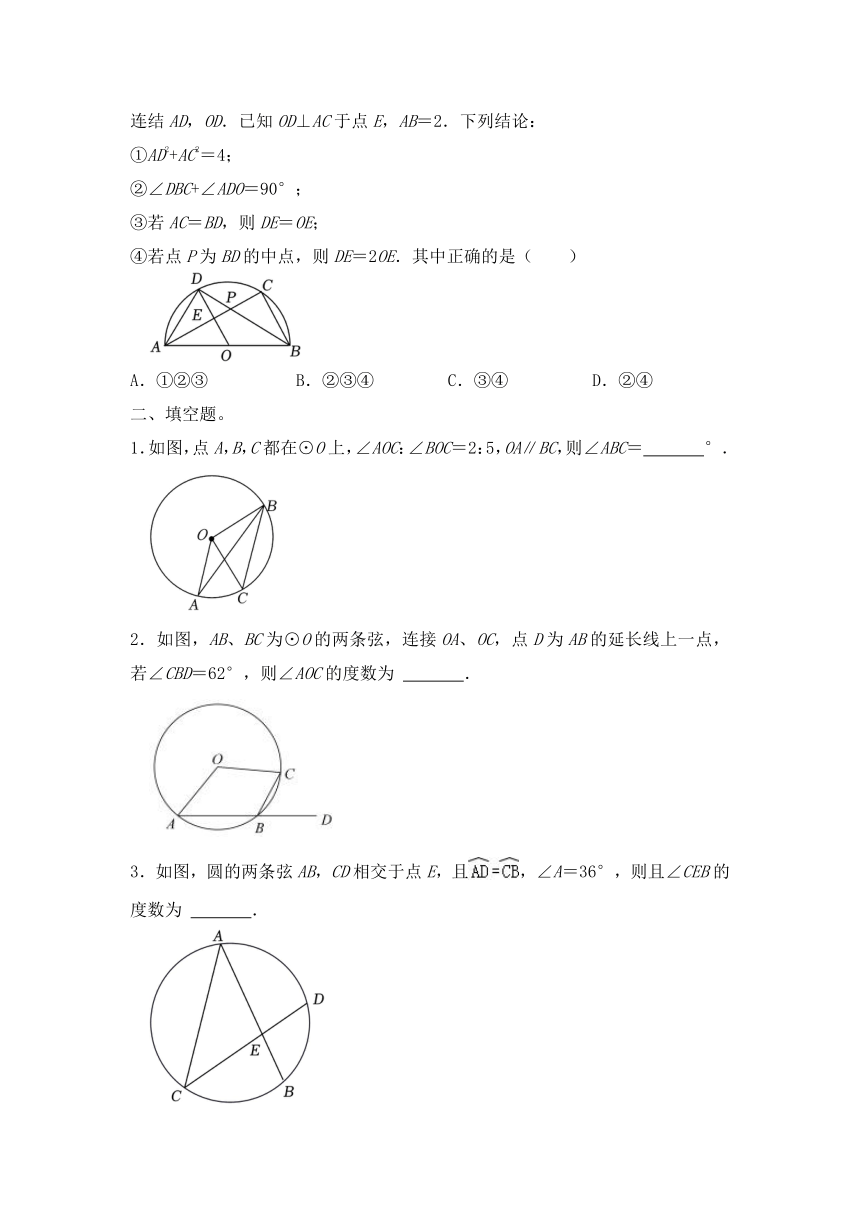
1.如图,已知AB是半⊙O的直径,点C,D都在上,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论错误的是( )
A.AD⊥BD B.AF=DF C.∠AOC=∠AEC D.BD=2OF
2.如图,AB是⊙O的直径,点C在⊙O上,半径OD⊥AC,连接BD,AD,若∠ABD=27°,则∠BAC是( )
A.27° B.36° C.53° D.54°
3.如图,线段AB是⊙O的直径,点C在圆上,∠AOC=60°,点P是线段AB延长线上的一点,连结PC,则∠APC的度数不可能是( )
A.30° B.25° C.10° D.5°
4.如图,点C,D在以AB为直径的⊙O上,且CD平分∠ACB,若CD=4,∠CAB=75°,则AB的长是( )
A.8 B.4 C.8 D.4
5.如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D(不与O重合),连结CD.若∠A=22°,则∠ACD的度数为( )
A.46° B.44° C.48° D.68°
6.如图,AB是半圆O的直径,点C、E是半圆上的动点(不与点A、B重合),且=,射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON=,交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )
A.先变大后变小 B.先变小后变大
C.保持不变 D.一直减小
7.如图,△ABC中,∠ACB=90°,AC=BC,点D是边AC上一动点,连接BD,以CD为直径的圆交BD于点E.若AB长为4,则线段AE长的最小值为( )
A. B. C. D.
8.如图,已知⊙O的半径为5,AB、CD为⊙O的弦,且CD=6.若∠AOB+∠COD=180°,则弦AB的长为( )
A.6 B.7 C.8 D.9
9.如图,AB为⊙O的直径,点C是AB上方半圆上的一点,点D是AB下方半圆的中点.连接AC,BC,AD,过点D作DE∥AB交CB的延长线于点E.若AD=5,则AC CE的最大值为( )
A.50 B.50 C.100 D.75
10.如图,BC为⊙O直径,点A,D在⊙O上,∠DAB=135°,若BC=4,则CD的长为( )
A.2 B.1 C. D.
11.如图,在⊙O中,AB为⊙O的弦,C为的中点,D为圆上一点,∠ADC=30°,⊙O的半径为4,则圆心O到弦AB的距离是( )
A.2 B.2 C.4 D.2
12.如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
①AD2+AC2=4;
②∠DBC+∠ADO=90°;
③若AC=BD,则DE=OE;
④若点P为BD的中点,则DE=2OE.其中正确的是( )
A.①②③ B.②③④ C.③④ D.②④
二、填空题。
1.如图,点A,B,C都在⊙O上,∠AOC:∠BOC=2:5,OA∥BC,则∠ABC= °.
2.如图,AB、BC为⊙O的两条弦,连接OA、OC,点D为AB的延长线上一点,若∠CBD=62°,则∠AOC的度数为 .
3.如图,圆的两条弦AB,CD相交于点E,且,∠A=36°,则且∠CEB的度数为 .
4.如图,AB、BC是以AC为直径的⊙O的两条弦,延长AC至点D,使CD=BC,则当∠D=15°时,AD与AB之间的数量关系为:AD= AB.
5.如图,在平面直角坐标系中,⊙M经过原点,且与x轴交于点A(4,0),与y轴交于点B,点C在第四象限的⊙M上,且∠AOC=60°,OC=3,则点B的坐标是 .
6.如图,在由边长为1的小正方形组成的网格中,一条弧经过格点(网格线的交点)A,B,D,点C为上一点.若∠CAD=30°,则的长为 .
三、解答题。
1.如图,⊙O中,=,∠C=70°,求∠A的度数.
2.如图,⊙O的半径为1,A、B、C是⊙O上的三个点,点P在劣弧AB上,∠APB=120°,PC平分∠APB.
(1)求证:PA+PB=PC;
(2)当点P位于什么位置时,△APB的面积最大?求出最大面积.
3.如图,C是的中点,∠AOC=4∠B,OC=4.
(1)求∠A的度数;
(2)求线段AB的长度.
4.如图,AB为⊙O的直径,C是⊙O上的一点,连接AC,BC.D是的中点,过D作DE⊥AB于点E,交BC于点F.
(1)求证:BC=2DE;
(2)若AC=6,AB=10,求DF的长.
5.已知:如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为的中点.
(1)求证:∠ACD=∠DEC;
(2)延长DE、CB交于点P,若PB=BO,DE=2,求PE的长.
6.如图,AB是⊙O的直径,点C在⊙O上且不与点A,B重合,∠ABC的平分线交⊙O于点D,过点D作DE⊥AB,垂足为点G,交⊙O于点E,连接CE交BD于点F,连接FG.
(1)求证:FG=DE;
(2)若AB=4,FG=4,求AG的长.
7.如图,AB是⊙O的直径,C,D是⊙O上两点,C是的中点,过点C作AD的垂线,垂足为E,连接AC交BD于点F.
(1)求证:CE是⊙O的切线;
(2)若DF=1,DC=,求⊙O的半径.
一、选择题。
1.如图,已知AB是半⊙O的直径,点C,D都在上,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论错误的是( )
A.AD⊥BD B.AF=DF C.∠AOC=∠AEC D.BD=2OF
2.如图,AB是⊙O的直径,点C在⊙O上,半径OD⊥AC,连接BD,AD,若∠ABD=27°,则∠BAC是( )
A.27° B.36° C.53° D.54°
3.如图,线段AB是⊙O的直径,点C在圆上,∠AOC=60°,点P是线段AB延长线上的一点,连结PC,则∠APC的度数不可能是( )
A.30° B.25° C.10° D.5°
4.如图,点C,D在以AB为直径的⊙O上,且CD平分∠ACB,若CD=4,∠CAB=75°,则AB的长是( )
A.8 B.4 C.8 D.4
5.如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D(不与O重合),连结CD.若∠A=22°,则∠ACD的度数为( )
A.46° B.44° C.48° D.68°
6.如图,AB是半圆O的直径,点C、E是半圆上的动点(不与点A、B重合),且=,射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON=,交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )
A.先变大后变小 B.先变小后变大
C.保持不变 D.一直减小
7.如图,△ABC中,∠ACB=90°,AC=BC,点D是边AC上一动点,连接BD,以CD为直径的圆交BD于点E.若AB长为4,则线段AE长的最小值为( )
A. B. C. D.
8.如图,已知⊙O的半径为5,AB、CD为⊙O的弦,且CD=6.若∠AOB+∠COD=180°,则弦AB的长为( )
A.6 B.7 C.8 D.9
9.如图,AB为⊙O的直径,点C是AB上方半圆上的一点,点D是AB下方半圆的中点.连接AC,BC,AD,过点D作DE∥AB交CB的延长线于点E.若AD=5,则AC CE的最大值为( )
A.50 B.50 C.100 D.75
10.如图,BC为⊙O直径,点A,D在⊙O上,∠DAB=135°,若BC=4,则CD的长为( )
A.2 B.1 C. D.
11.如图,在⊙O中,AB为⊙O的弦,C为的中点,D为圆上一点,∠ADC=30°,⊙O的半径为4,则圆心O到弦AB的距离是( )
A.2 B.2 C.4 D.2
12.如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
①AD2+AC2=4;
②∠DBC+∠ADO=90°;
③若AC=BD,则DE=OE;
④若点P为BD的中点,则DE=2OE.其中正确的是( )
A.①②③ B.②③④ C.③④ D.②④
二、填空题。
1.如图,点A,B,C都在⊙O上,∠AOC:∠BOC=2:5,OA∥BC,则∠ABC= °.
2.如图,AB、BC为⊙O的两条弦,连接OA、OC,点D为AB的延长线上一点,若∠CBD=62°,则∠AOC的度数为 .
3.如图,圆的两条弦AB,CD相交于点E,且,∠A=36°,则且∠CEB的度数为 .
4.如图,AB、BC是以AC为直径的⊙O的两条弦,延长AC至点D,使CD=BC,则当∠D=15°时,AD与AB之间的数量关系为:AD= AB.
5.如图,在平面直角坐标系中,⊙M经过原点,且与x轴交于点A(4,0),与y轴交于点B,点C在第四象限的⊙M上,且∠AOC=60°,OC=3,则点B的坐标是 .
6.如图,在由边长为1的小正方形组成的网格中,一条弧经过格点(网格线的交点)A,B,D,点C为上一点.若∠CAD=30°,则的长为 .
三、解答题。
1.如图,⊙O中,=,∠C=70°,求∠A的度数.
2.如图,⊙O的半径为1,A、B、C是⊙O上的三个点,点P在劣弧AB上,∠APB=120°,PC平分∠APB.
(1)求证:PA+PB=PC;
(2)当点P位于什么位置时,△APB的面积最大?求出最大面积.
3.如图,C是的中点,∠AOC=4∠B,OC=4.
(1)求∠A的度数;
(2)求线段AB的长度.
4.如图,AB为⊙O的直径,C是⊙O上的一点,连接AC,BC.D是的中点,过D作DE⊥AB于点E,交BC于点F.
(1)求证:BC=2DE;
(2)若AC=6,AB=10,求DF的长.
5.已知:如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为的中点.
(1)求证:∠ACD=∠DEC;
(2)延长DE、CB交于点P,若PB=BO,DE=2,求PE的长.
6.如图,AB是⊙O的直径,点C在⊙O上且不与点A,B重合,∠ABC的平分线交⊙O于点D,过点D作DE⊥AB,垂足为点G,交⊙O于点E,连接CE交BD于点F,连接FG.
(1)求证:FG=DE;
(2)若AB=4,FG=4,求AG的长.
7.如图,AB是⊙O的直径,C,D是⊙O上两点,C是的中点,过点C作AD的垂线,垂足为E,连接AC交BD于点F.
(1)求证:CE是⊙O的切线;
(2)若DF=1,DC=,求⊙O的半径.
同课章节目录
