勾股定理基础知识回顾
图片预览







文档简介
课件23张PPT。华东师大版:初中数学期末复习-勾股定理制作: 泸县石桥中学
戴剑峰 课题:
勾股定理的基础回顾与复习
1.直角三角形的两条直角边的长分别是3cm和4cm,则斜边的长是_______.
2.斜边为13cm,一条直角边长为12cm,则另一条直角边为_______.
3.若一个直角三角形的斜边是20cm,两条直角边的比是3∶4,则较短的直角边是_______. 课前三分钟检测4.等腰三角形的底边为10cm,周长为36cm,则它的面积是_________.
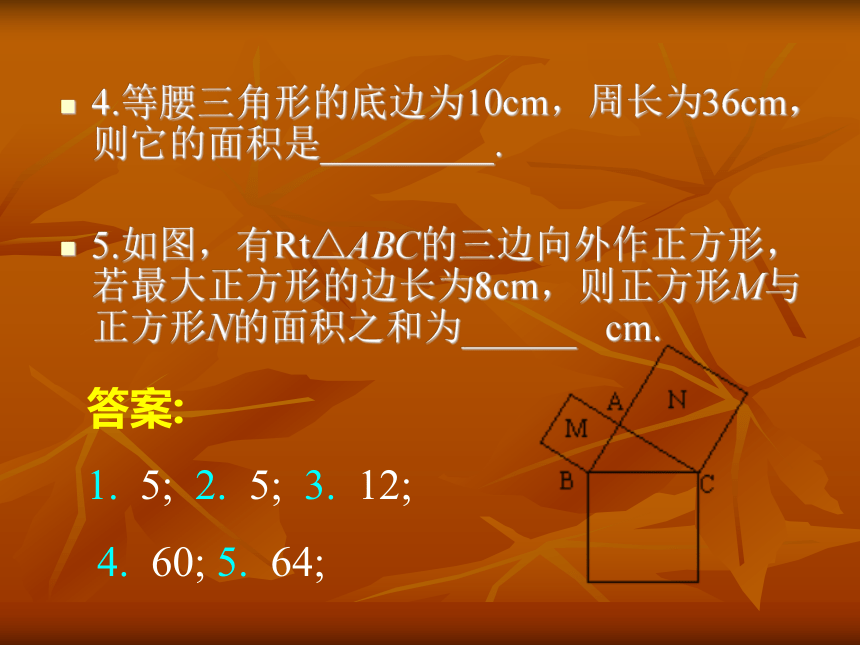
5.如图,有Rt△ABC的三边向外作正方形,若最大正方形的边长为8cm,则正方形M与正方形N的面积之和为______ cm. 答案:
1. 5; 2. 5; 3. 12;
4. 60; 5. 64;课标要求回顾课标和知识要求1.了解直角三角形的概念,探索并掌握直角三角形的性质.
2.探索并掌握一个三角形是直角三角形的条件.
3.体验勾股定理的探索过程,会运用勾股定理解决简单问题;
4.会用勾股定理的逆定理判定直角三角形。1、直角三角形基本元素之间的关系.
如上图,在三角形ABC中,∠C=900.
角的关系:∠A+∠b=900
边的关系:(勾股定理) a2+b2=c2。
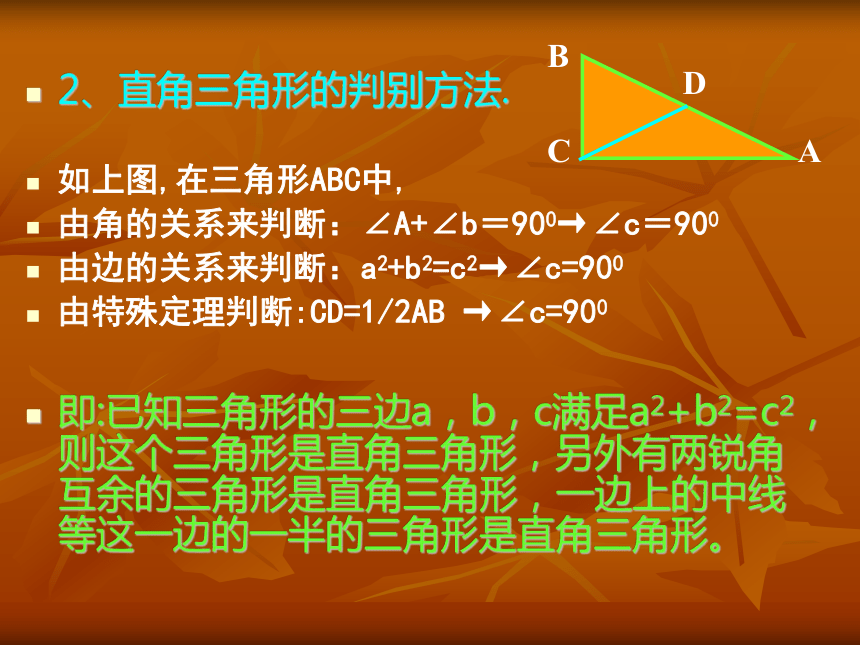
边角关系: 如果∠A=300,则AB=2BC.回顾基础知识和基础方法2、直角三角形的判别方法.
如上图,在三角形ABC中,
由角的关系来判断:∠A+∠b=900→∠c=900
由边的关系来判断:a2+b2=c2→∠c=900
由特殊定理判断:CD=1/2AB →∠c=900
即:已知三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形,另外有两锐角互余的三角形是直角三角形,一边上的中线等这一边的一半的三角形是直角三角形。3、定义及常见的勾股数:
勾股数:满足a2 + b2 = c2的三个正整数,称为勾股数。
常用的勾股数:如3、4、5;5、12、13;6、8、10;12、16、20.
勾股数特点:同一组勾股定理数,每一个勾股定理数乘以相同的正整数倍数,得到的仍然是勾股定理数,4、方法和要点:
数形相互转变的思想方法.
表面路径最短的问题,一般用侧面展开法,展成平面后,运用勾股定理.
空间距离问题,一般从立体图形中找到直角三角形并运用勾股定理.
解直角三角形与实际问题联系起来,在解决实际问题时,应养成“先画图,再求解”的习惯.
不能简单地将解直角三角形的应用分为几种问题类型,注意问题选取的多样性。合理地选择关系式。
考试时,填空题——耐心填一填,选择题——精心选一选,计算题——细心算一算,解答题——用心想一想题型:
利用勾股定理计算;
证明带有平方的问题;
判断某三角形是否为直角三角形;
利用勾股定理的实际应用。5、题型与注意点注意:
无直角时,可作垂线构造直角三角形;
三角形中较小两边的平方和等于较大边的平方时,才可判断这个三角形是直角三角形,且较大边所对的角是直角,
不能认为c边所对的角必是直角。
运用时首先确定最大边,要先确定斜边; 。基础知识应用举例一、直角三角形基本元素与主要元素关系例题1:在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
求Rt△ABC的周长、面积以及斜边上的中线、角平分线、高. 反思:解直角三角形三边的关系是求其它主要元素的基础,要注意列方程思想在求其它元素上的应用,其中,两直角边的乘积等于斜边与其高的乘积应当引起重视例题2:课本P63:7. 有一块四边形地ABCD(如图),∠B=90°, AB=4m, BC=3m, CD=12m, DA=13m, 求该四边形地ABCD的面积.341213?431213反思:勾股定理在四边形中的应用,基本内核是作四边形的对角线转化为三角形,用勾股定理和其逆定理相互转化问题,从而求解其它的量.二、勾股定理与平面图形ACBabc 与直角三角形的边有关的面积中,注意以上图形的特点:两直角边有关的两个小的图形面积之和等于斜边有关的图形面积。例题1:如图:它是分别以直角三角形ABC的三边为直径向上作三个半圆,图中阴影部分的面积与直角三角形、半圆之间有什么关系?分析:
阴影面积
=两个小半圆面积+直角三角形面积-大半圆面积
=直角三角形面积。例题2:如图:它是分别以直角三角形ABC的两直角边为直径作的二个半圆,图中阴影部分的面积与直角三角形、半圆之间有什么关系?分析:
阴影面积
=两个小半圆面积-直角三角形面积。
反思:我们自己通过拼接图形,理解以上关系,同时记住这些关系有利于提高我们观察图形的能力例题1:下图由4个等腰直角三角形组成,其中第1个直角三角形腰长为1cm,求第4个直角三角形斜边长度.三、勾股树与变动的直角三角形例题2: 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,求正方形A、 B、 C、 D的面积和.
例题4、正方形ABCD边长为a=1,写出第n个正方形的边长an?例题3、第一个正方形的边长为8,求第7个正方形的边长?反思:注意这种有规律性的与勾股定理有关的问题,以便于我们更简捷的解答问题。四、勾股定理的应用问题
ACBX10-X3例题1、课本P63C组:12. 折竹抵地(源自《九章算术》):今有竹高一丈,末折抵地,去本三尺.问折者高几何?意即: 一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹 梢恰好抵地,抵地处离原长竹子处3尺远.问原处还有多高的竹子? 实际问题应用题转化为数学问题,涉及图形必须转化为几何图形,也可以在原图形上画,也可以另外图,但画出的几何图形一定要标出字母,便于解答问题时叙述。ACB8101DE例题2:若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远?反思:实际问题的所设未知,有直接和间接设法,问题的求解有一些基本程序,要注意这种典型的应用问题:滑梯问题;还有如:蚂蚁爬行问题。1.直角三角形的一直角边长是12,斜边长是15,则另一直角边是(???? ).?
(A)8? ?(B)9? (C)10? (D)11基础知识应用训练2.等边三角形的边长为a,则三角形的高为(???? ).
(A) ?(B)? (C)? (D)a3.直角三角形的两条直角边的长分别是6cm和8cm,则斜边上的中线为(???? ).
?(A)10? (B)7 ?(C)5或7 (D)54、等腰直角三角形的斜边是任一直角边的(???? ).
?(A)一半? (B)2 倍? (C) 倍? (D) 倍5.在含30°的直角三角形中,30°角相邻的直角边为6,则其它两边长为(???? ).?
(A)9和12? (B)3和3 .
(C) ?(D)3和4 6.一个等腰直角三角形的斜边为4,则其面积为(???? ).
?(A)2? (B)4? (C)8? (D)4 7.若直角三角形的两条直角边各扩大一倍,则斜边扩大(???? ).
?(A)不变?.(B)一倍.?(C)两倍.?(D)无法确定答案:
1.B; 2.B; 3.D; 4.C; 5.C; 6.B; 7.B.课外书面作业课本:P62:复习题2题、4题、10题。复习小结复习内容有:
勾股定理基本知识和要求
勾股定理解题举例
勾股定理基础训练同学们,本课结束,下节课再见!同学们再见
戴剑峰 课题:
勾股定理的基础回顾与复习
1.直角三角形的两条直角边的长分别是3cm和4cm,则斜边的长是_______.
2.斜边为13cm,一条直角边长为12cm,则另一条直角边为_______.
3.若一个直角三角形的斜边是20cm,两条直角边的比是3∶4,则较短的直角边是_______. 课前三分钟检测4.等腰三角形的底边为10cm,周长为36cm,则它的面积是_________.
5.如图,有Rt△ABC的三边向外作正方形,若最大正方形的边长为8cm,则正方形M与正方形N的面积之和为______ cm. 答案:
1. 5; 2. 5; 3. 12;
4. 60; 5. 64;课标要求回顾课标和知识要求1.了解直角三角形的概念,探索并掌握直角三角形的性质.
2.探索并掌握一个三角形是直角三角形的条件.
3.体验勾股定理的探索过程,会运用勾股定理解决简单问题;
4.会用勾股定理的逆定理判定直角三角形。1、直角三角形基本元素之间的关系.
如上图,在三角形ABC中,∠C=900.
角的关系:∠A+∠b=900
边的关系:(勾股定理) a2+b2=c2。
边角关系: 如果∠A=300,则AB=2BC.回顾基础知识和基础方法2、直角三角形的判别方法.
如上图,在三角形ABC中,
由角的关系来判断:∠A+∠b=900→∠c=900
由边的关系来判断:a2+b2=c2→∠c=900
由特殊定理判断:CD=1/2AB →∠c=900
即:已知三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形,另外有两锐角互余的三角形是直角三角形,一边上的中线等这一边的一半的三角形是直角三角形。3、定义及常见的勾股数:
勾股数:满足a2 + b2 = c2的三个正整数,称为勾股数。
常用的勾股数:如3、4、5;5、12、13;6、8、10;12、16、20.
勾股数特点:同一组勾股定理数,每一个勾股定理数乘以相同的正整数倍数,得到的仍然是勾股定理数,4、方法和要点:
数形相互转变的思想方法.
表面路径最短的问题,一般用侧面展开法,展成平面后,运用勾股定理.
空间距离问题,一般从立体图形中找到直角三角形并运用勾股定理.
解直角三角形与实际问题联系起来,在解决实际问题时,应养成“先画图,再求解”的习惯.
不能简单地将解直角三角形的应用分为几种问题类型,注意问题选取的多样性。合理地选择关系式。
考试时,填空题——耐心填一填,选择题——精心选一选,计算题——细心算一算,解答题——用心想一想题型:
利用勾股定理计算;
证明带有平方的问题;
判断某三角形是否为直角三角形;
利用勾股定理的实际应用。5、题型与注意点注意:
无直角时,可作垂线构造直角三角形;
三角形中较小两边的平方和等于较大边的平方时,才可判断这个三角形是直角三角形,且较大边所对的角是直角,
不能认为c边所对的角必是直角。
运用时首先确定最大边,要先确定斜边; 。基础知识应用举例一、直角三角形基本元素与主要元素关系例题1:在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
求Rt△ABC的周长、面积以及斜边上的中线、角平分线、高. 反思:解直角三角形三边的关系是求其它主要元素的基础,要注意列方程思想在求其它元素上的应用,其中,两直角边的乘积等于斜边与其高的乘积应当引起重视例题2:课本P63:7. 有一块四边形地ABCD(如图),∠B=90°, AB=4m, BC=3m, CD=12m, DA=13m, 求该四边形地ABCD的面积.341213?431213反思:勾股定理在四边形中的应用,基本内核是作四边形的对角线转化为三角形,用勾股定理和其逆定理相互转化问题,从而求解其它的量.二、勾股定理与平面图形ACBabc 与直角三角形的边有关的面积中,注意以上图形的特点:两直角边有关的两个小的图形面积之和等于斜边有关的图形面积。例题1:如图:它是分别以直角三角形ABC的三边为直径向上作三个半圆,图中阴影部分的面积与直角三角形、半圆之间有什么关系?分析:
阴影面积
=两个小半圆面积+直角三角形面积-大半圆面积
=直角三角形面积。例题2:如图:它是分别以直角三角形ABC的两直角边为直径作的二个半圆,图中阴影部分的面积与直角三角形、半圆之间有什么关系?分析:
阴影面积
=两个小半圆面积-直角三角形面积。
反思:我们自己通过拼接图形,理解以上关系,同时记住这些关系有利于提高我们观察图形的能力例题1:下图由4个等腰直角三角形组成,其中第1个直角三角形腰长为1cm,求第4个直角三角形斜边长度.三、勾股树与变动的直角三角形例题2: 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,求正方形A、 B、 C、 D的面积和.
例题4、正方形ABCD边长为a=1,写出第n个正方形的边长an?例题3、第一个正方形的边长为8,求第7个正方形的边长?反思:注意这种有规律性的与勾股定理有关的问题,以便于我们更简捷的解答问题。四、勾股定理的应用问题
ACBX10-X3例题1、课本P63C组:12. 折竹抵地(源自《九章算术》):今有竹高一丈,末折抵地,去本三尺.问折者高几何?意即: 一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹 梢恰好抵地,抵地处离原长竹子处3尺远.问原处还有多高的竹子? 实际问题应用题转化为数学问题,涉及图形必须转化为几何图形,也可以在原图形上画,也可以另外图,但画出的几何图形一定要标出字母,便于解答问题时叙述。ACB8101DE例题2:若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远?反思:实际问题的所设未知,有直接和间接设法,问题的求解有一些基本程序,要注意这种典型的应用问题:滑梯问题;还有如:蚂蚁爬行问题。1.直角三角形的一直角边长是12,斜边长是15,则另一直角边是(???? ).?
(A)8? ?(B)9? (C)10? (D)11基础知识应用训练2.等边三角形的边长为a,则三角形的高为(???? ).
(A) ?(B)? (C)? (D)a3.直角三角形的两条直角边的长分别是6cm和8cm,则斜边上的中线为(???? ).
?(A)10? (B)7 ?(C)5或7 (D)54、等腰直角三角形的斜边是任一直角边的(???? ).
?(A)一半? (B)2 倍? (C) 倍? (D) 倍5.在含30°的直角三角形中,30°角相邻的直角边为6,则其它两边长为(???? ).?
(A)9和12? (B)3和3 .
(C) ?(D)3和4 6.一个等腰直角三角形的斜边为4,则其面积为(???? ).
?(A)2? (B)4? (C)8? (D)4 7.若直角三角形的两条直角边各扩大一倍,则斜边扩大(???? ).
?(A)不变?.(B)一倍.?(C)两倍.?(D)无法确定答案:
1.B; 2.B; 3.D; 4.C; 5.C; 6.B; 7.B.课外书面作业课本:P62:复习题2题、4题、10题。复习小结复习内容有:
勾股定理基本知识和要求
勾股定理解题举例
勾股定理基础训练同学们,本课结束,下节课再见!同学们再见
