人教A版(2019)必修第一册 3.2.2奇偶性 课件(共20张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 3.2.2奇偶性 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
函数的奇偶性
对 称
是整个中国的基因
文化基因是看不见的对称轴
沿着这条对称轴走进中国 .......
创设情境 兴趣导入
ADD TITLE
add your words here,according to your need to draw the text box size
AD TITLE
add your words here,according to your need to draw the text box size
脸 谱 艺 术
轴对称
把一个图形沿着某一条直线折叠,如果它能与另外一个图形重合,称这两个图形轴对称.
中心对称
把一个图形绕着某一个点旋转 ,如果它能够与另一个图形重合,那么说这两个图形关于这个点中心对称.
温故知新 循序渐进
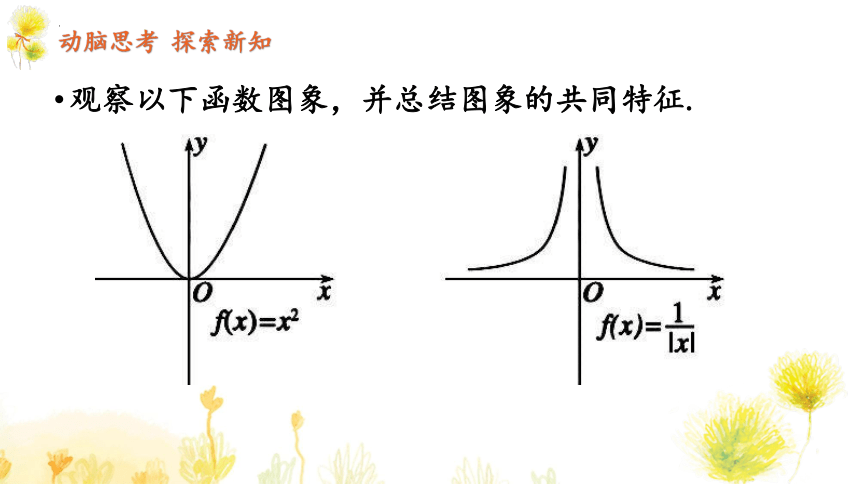
观察以下函数图象,并总结图象的共同特征.
动脑思考 探索新知
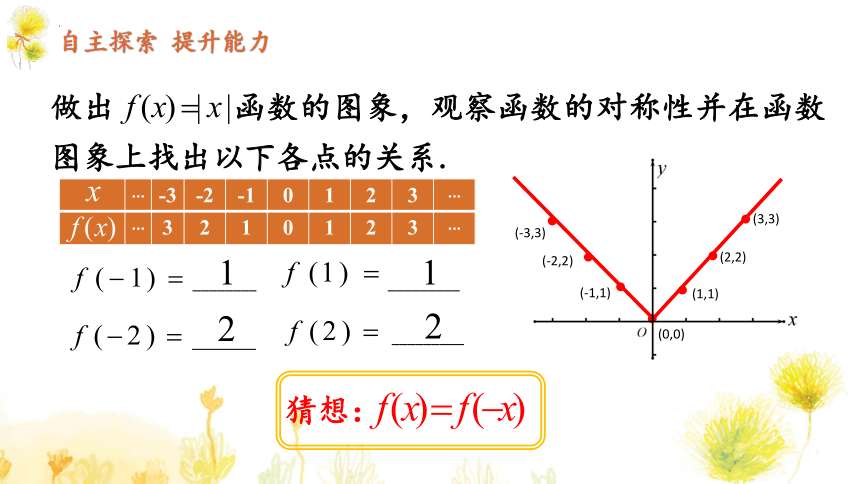
做出 函数的图象,观察函数的对称性并在函数图象上找出以下各点的关系.
... -3 -2 -1 0 1 2 3 ...
... 3 2 1 0 1 2 3 ...
猜想:
_________
_________
________
________
(-3,3)
(-2,2)
(-1,1)
(0,0)
(3,3)
(2,2)
(1,1)
自主探索 提升能力
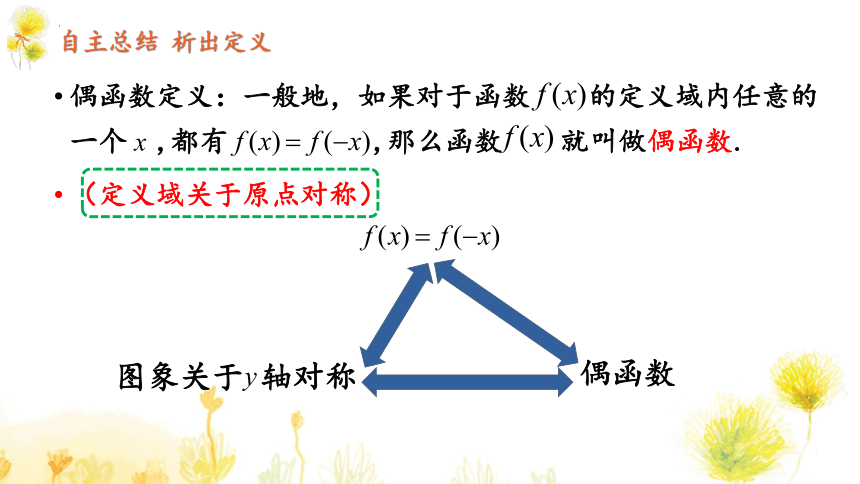
偶函数定义:一般地,如果对于函数 的定义域内任意的一个 ,都有 ,那么函数 就叫做偶函数.
(定义域关于原点对称)
偶函数
图象关于 轴对称
自主总结 析出定义
Add your words here,according to your need to draw the text box size。Please read the instructions and more work at the end of the manual template.
判断下列函数是否为偶函数.
(1)解
即
是偶函数.
的定义域为
又
是
巩固知识 典型例题
Add your words here,according to your need to draw the text box size。Please read the instructions and more work at the end of the manual template.
(2)解
是
不是
即定义域不关于原点对称,
不是偶函数
的定义域为
判断下列函数是否为偶函数.
巩固知识 典型例题
Add your words here,according to your need to draw the text box size。Please read the instructions and more work at the end of the manual template.
下列函数图象有什么共同特征?
合作探究 类比发现
做出 的函数的图象,观察函数的对称性,并在函数图象上找出以下各点的关系.
... -3 -2 -1 0 1 2 3 ...
... -3 -2 -1 0 1 2 3 ...
猜想:
________
________
________
________
(-2,-2)
(-1,-1)
(0,0)
(1,1)
(2,2)
(3,3)
自主探索 提升能力
奇函数定义:一般地,如果对于函数 的定义域内任意一个 ,都有 ,那么函数 就叫做奇函数.
(定义域关于原点对称)
图象关于原点对称
奇函数
自主总结 析出定义
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
是奇函数.
的定义域为
又
(1)解
运用知识 强化练习
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
偶函数
(2)解
是偶函数.
的定义域为
又
运用知识 强化练习
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
偶函数
非奇非偶函数
的定义域为
又
(3)解
是非奇非偶函数.
且
运用知识 强化练习
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
偶函数
非奇非偶函数
既奇又偶函数
(4)解
是既奇又偶函数.
的定义域为
又
且
运用知识 强化练习
(1)解:
即
不是偶函数.
又
(1)解:
是奇函数.
的定义域为
又
奇函数
偶函数
既奇又偶函数
非奇非偶函数
根据函数的奇偶性,将函数分为以下四类.
归纳小结 强化思想
一看
二找
三判断
看定义域
找关系
下结论
与
奇或偶
是否关于原点对称
归纳小结 强化思想
必做题:课本第36页练习题第1-2题.
选做题:课本第39页习题1.3A组第6题.
思考题:课本第39页习题1.3B组第3题.
巩固提高 作业布置
谢 谢
函数的奇偶性
对 称
是整个中国的基因
文化基因是看不见的对称轴
沿着这条对称轴走进中国 .......
创设情境 兴趣导入
ADD TITLE
add your words here,according to your need to draw the text box size
AD TITLE
add your words here,according to your need to draw the text box size
脸 谱 艺 术
轴对称
把一个图形沿着某一条直线折叠,如果它能与另外一个图形重合,称这两个图形轴对称.
中心对称
把一个图形绕着某一个点旋转 ,如果它能够与另一个图形重合,那么说这两个图形关于这个点中心对称.
温故知新 循序渐进
观察以下函数图象,并总结图象的共同特征.
动脑思考 探索新知
做出 函数的图象,观察函数的对称性并在函数图象上找出以下各点的关系.
... -3 -2 -1 0 1 2 3 ...
... 3 2 1 0 1 2 3 ...
猜想:
_________
_________
________
________
(-3,3)
(-2,2)
(-1,1)
(0,0)
(3,3)
(2,2)
(1,1)
自主探索 提升能力
偶函数定义:一般地,如果对于函数 的定义域内任意的一个 ,都有 ,那么函数 就叫做偶函数.
(定义域关于原点对称)
偶函数
图象关于 轴对称
自主总结 析出定义
Add your words here,according to your need to draw the text box size。Please read the instructions and more work at the end of the manual template.
判断下列函数是否为偶函数.
(1)解
即
是偶函数.
的定义域为
又
是
巩固知识 典型例题
Add your words here,according to your need to draw the text box size。Please read the instructions and more work at the end of the manual template.
(2)解
是
不是
即定义域不关于原点对称,
不是偶函数
的定义域为
判断下列函数是否为偶函数.
巩固知识 典型例题
Add your words here,according to your need to draw the text box size。Please read the instructions and more work at the end of the manual template.
下列函数图象有什么共同特征?
合作探究 类比发现
做出 的函数的图象,观察函数的对称性,并在函数图象上找出以下各点的关系.
... -3 -2 -1 0 1 2 3 ...
... -3 -2 -1 0 1 2 3 ...
猜想:
________
________
________
________
(-2,-2)
(-1,-1)
(0,0)
(1,1)
(2,2)
(3,3)
自主探索 提升能力
奇函数定义:一般地,如果对于函数 的定义域内任意一个 ,都有 ,那么函数 就叫做奇函数.
(定义域关于原点对称)
图象关于原点对称
奇函数
自主总结 析出定义
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
是奇函数.
的定义域为
又
(1)解
运用知识 强化练习
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
偶函数
(2)解
是偶函数.
的定义域为
又
运用知识 强化练习
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
偶函数
非奇非偶函数
的定义域为
又
(3)解
是非奇非偶函数.
且
运用知识 强化练习
判断下列函数的奇偶性:
(1)解:
的定义域为
即
不是偶函数.
又
奇函数
(1)解:
是奇函数.
的定义域为
又
偶函数
非奇非偶函数
既奇又偶函数
(4)解
是既奇又偶函数.
的定义域为
又
且
运用知识 强化练习
(1)解:
即
不是偶函数.
又
(1)解:
是奇函数.
的定义域为
又
奇函数
偶函数
既奇又偶函数
非奇非偶函数
根据函数的奇偶性,将函数分为以下四类.
归纳小结 强化思想
一看
二找
三判断
看定义域
找关系
下结论
与
奇或偶
是否关于原点对称
归纳小结 强化思想
必做题:课本第36页练习题第1-2题.
选做题:课本第39页习题1.3A组第6题.
思考题:课本第39页习题1.3B组第3题.
巩固提高 作业布置
谢 谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
