人教版小数五年级上册 5.5 基本方程的解法 课件
文档属性
| 名称 | 人教版小数五年级上册 5.5 基本方程的解法 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 16:00:05 | ||
图片预览






文档简介
(共30张PPT)
解方程
人教版 五年级上册
情境导入
猜一猜:下面的盒子里可能有几个球
情境导入
现在已知箱子里的球再加上3个球共9个球
可以是任意数!
小组讨论:箱子里有几个球
例题探求
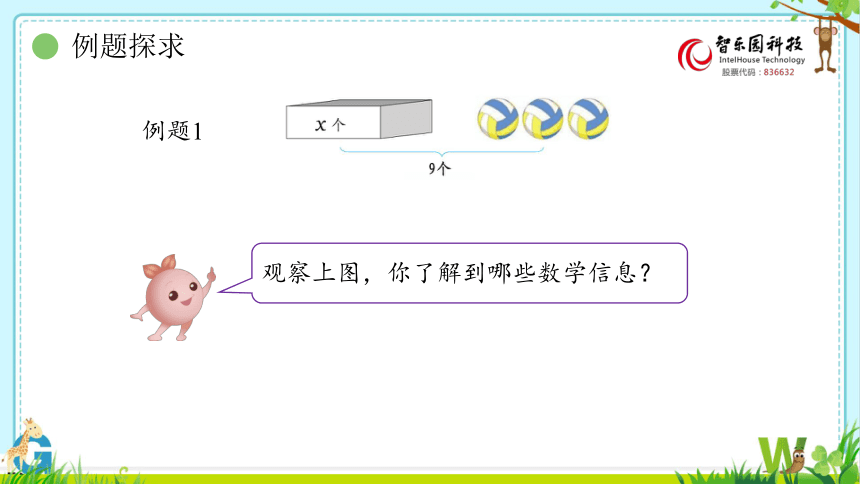
例题1
观察上图,你了解到哪些数学信息?
例题探求
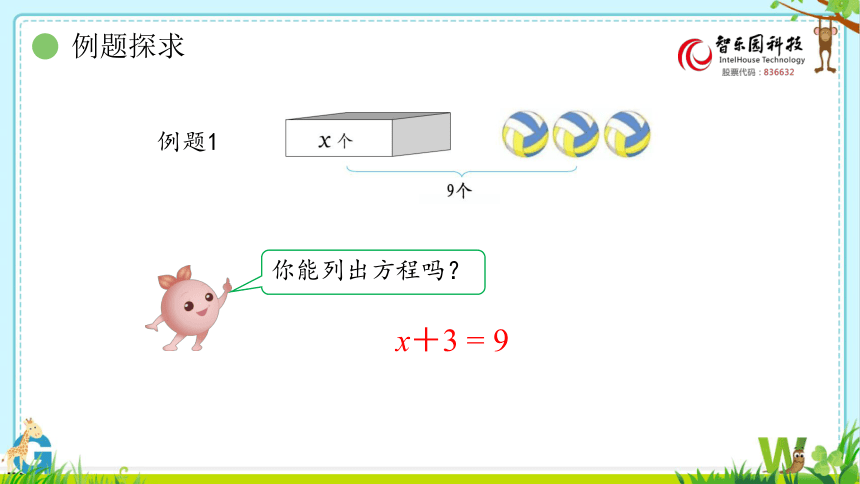
例题1
你能列出方程吗?
x+3 = 9
例题探求
x+3 = 9
x的值是多少?
说一说:你是怎样想的?
例题探求
方法一:
x+3=9
由 9 – 3 = 6,
想 6 + 3 = 9,
所以 ,x = 6。
例题探求
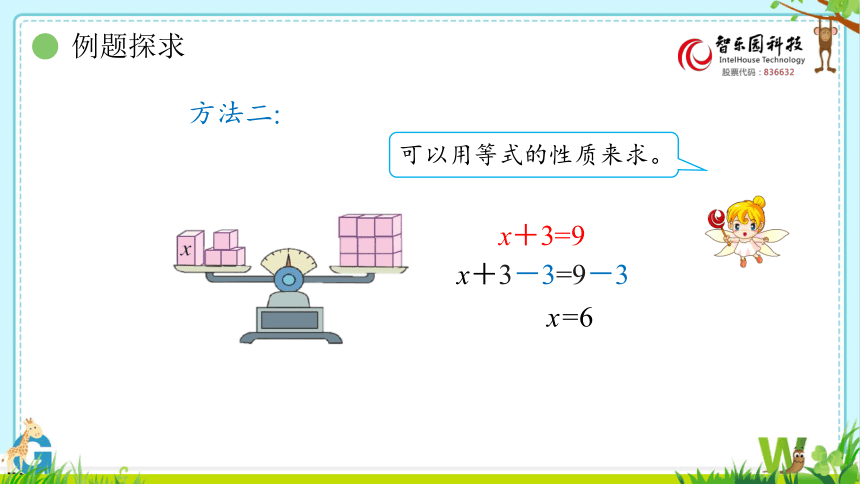
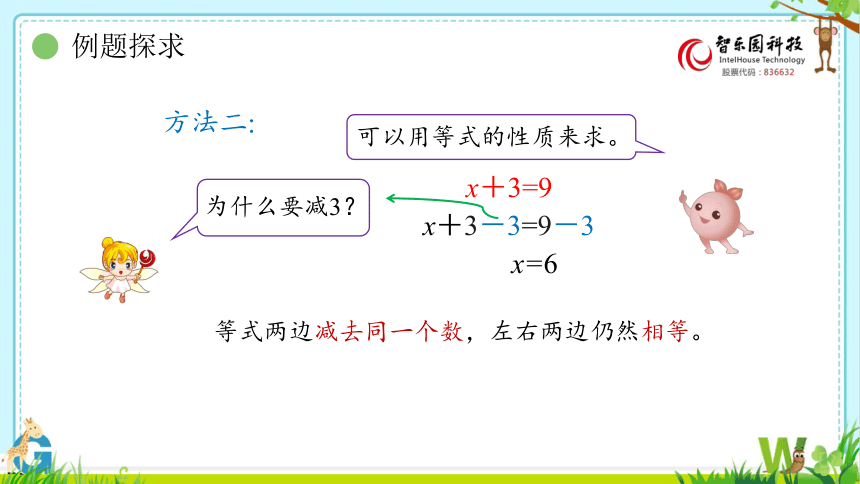
方法二:
x+3=9
可以用等式的性质来求。
x+3-3=9-3
x=6
例题探求
方法二:
x+3=9
可以用等式的性质来求。
x+3-3=9-3
x=6
为什么要减3?
等式两边减去同一个数,左右两边仍然相等。
例题探求
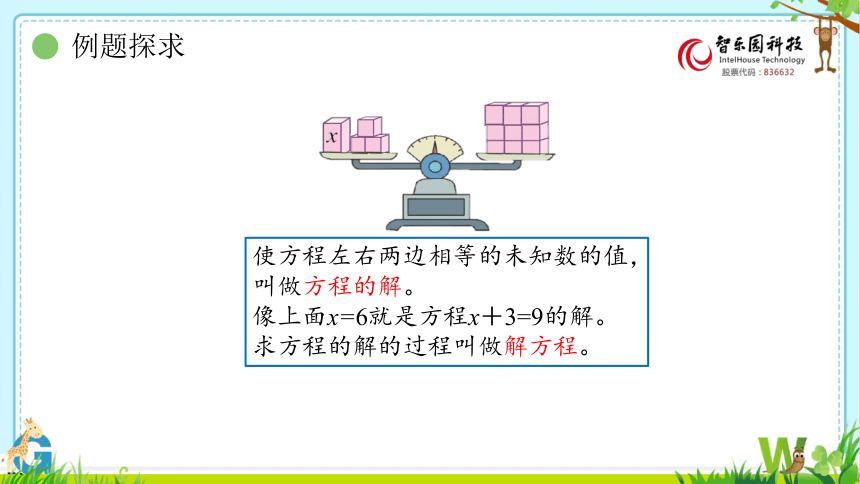
使方程左右两边相等的未知数的值,叫做方程的解。
像上面x=6就是方程x+3=9的解。求方程的解的过程叫做解方程。
例题探求
今后我们就可以用等式的性质来求解方程中未知数的值。
那么这个演算过程应如何书写呢?
例题探求
x+3 = 9
解:x +3-3 = 9-3
x = 6
从方程的第二行起写一个“解:”,利用等式的性质两边同时减去一个数,为了美观,要注意每步等号要对齐。
例题探求
=6+3
=9
=方程右边
所以,x=6是方程的解。
方程左边=x+3
x = 6 是不是正确的答案呢?检验一下。
x+3=9
例题探求
解方程 3x = 18。
例题2
说一说你的想法。
例题探求
3x = 18
解:3x÷( ) = 18÷( )
x = ( )
3
3
6
我是借助天平来解答的。
例题探求
3x = 18
解:3x÷( ) = 18÷( )
x = ( )
3
3
6
依据是什么?
等式两边除以同一个不等于0的数,左右两边仍然相等
例题探求
规范解答:
解方程 3x = 18。
3x = 18
解:3x÷3 = 18÷3
x = 6
例题2
例题探求
解方程 20-x = 9
例题3
说一说你的想法。
你遇到了什么困难?
例题探求
解方程 20-x = 9
例题3
说一说你的想法。
你遇到了什么困难?
例题探求
规范解答:
20-x = 9
x = 11
解:20-x+x = 9+x
20 = 9+x
9+x = 20
9+x-9 = 20-9
等式两边加上相同的式子,左右两边仍然相等。
+x
+x
例题探求
x = 11是不是正确的答案呢?检验一下。
检验:
方程左边 = 20 - x
= 20 - 11
= 9
=方程右边
所以,x = 11是方程的解。
20-x = 9
小小练习
4 元
x元
1.2元
解:x = 4 – 1.2
x + 1.2= 4
x = 2.8
列方程并解答。
小小练习
8.4 元
x元
x元
x元
解:3x÷3 = 8.4÷3
3x = 8.4
x = 2.8
列方程并解答。
小小练习
(1)解方程4x = 28时,方程两边要同时( )。
(2)解方程x÷5 = 9时,方程两边要同时( ) 。
(3)方程9x = 10.8的解是( ) 。
除以4
乘5
1.2
我会填。
小小练习
(1)x+3.2 = 4.6
解:x+3.2-3.2 = 4.6-3.2
x = 1.4
解:x-1.8+1.8 = 4+1.8
x = 5.8
解下列方程。
(2)x-1.8 = 4
小小练习
(3)15 - x = 2
解: 15-x+x = 2+x
15 = 2+x
2+x = 15
2+x-2 = 15-2
x = 13
解:1.6x÷1.6 = 6.4÷1.6
x = 4
解下列方程。
(4)1.6x = 6.4
小小练习
(5)x÷7 = 0.3
解:x÷7 ×7= 0.3 ×7
x = 2.1
解: 2.1÷x×x = 3×x
2.1 = 3x
3x = 2.1
3x÷3 = 2.1÷3
x = 0.7
解下列方程。
(6)2.1÷x = 3
小小练习
一块长方形菜地的面积是259平方米,这块菜地的长是18.5米,宽是x米。请你列出方程并解答。
解:18.5x = 259
18.5x÷18.5 = 259 ÷18.5
x = 14
答:宽是 14 米。
归纳小结
这节课你们都学会了哪些知识?
解简单的方程
解方程
形如ax = b的方程
解:ax÷a=b÷a
x=b÷a
形如a - x = b的方程
解:a – x + x= b + x
b + x = a
x = a - b
等式的性质2
等式的性质1
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
解方程
人教版 五年级上册
情境导入
猜一猜:下面的盒子里可能有几个球
情境导入
现在已知箱子里的球再加上3个球共9个球
可以是任意数!
小组讨论:箱子里有几个球
例题探求
例题1
观察上图,你了解到哪些数学信息?
例题探求
例题1
你能列出方程吗?
x+3 = 9
例题探求
x+3 = 9
x的值是多少?
说一说:你是怎样想的?
例题探求
方法一:
x+3=9
由 9 – 3 = 6,
想 6 + 3 = 9,
所以 ,x = 6。
例题探求
方法二:
x+3=9
可以用等式的性质来求。
x+3-3=9-3
x=6
例题探求
方法二:
x+3=9
可以用等式的性质来求。
x+3-3=9-3
x=6
为什么要减3?
等式两边减去同一个数,左右两边仍然相等。
例题探求
使方程左右两边相等的未知数的值,叫做方程的解。
像上面x=6就是方程x+3=9的解。求方程的解的过程叫做解方程。
例题探求
今后我们就可以用等式的性质来求解方程中未知数的值。
那么这个演算过程应如何书写呢?
例题探求
x+3 = 9
解:x +3-3 = 9-3
x = 6
从方程的第二行起写一个“解:”,利用等式的性质两边同时减去一个数,为了美观,要注意每步等号要对齐。
例题探求
=6+3
=9
=方程右边
所以,x=6是方程的解。
方程左边=x+3
x = 6 是不是正确的答案呢?检验一下。
x+3=9
例题探求
解方程 3x = 18。
例题2
说一说你的想法。
例题探求
3x = 18
解:3x÷( ) = 18÷( )
x = ( )
3
3
6
我是借助天平来解答的。
例题探求
3x = 18
解:3x÷( ) = 18÷( )
x = ( )
3
3
6
依据是什么?
等式两边除以同一个不等于0的数,左右两边仍然相等
例题探求
规范解答:
解方程 3x = 18。
3x = 18
解:3x÷3 = 18÷3
x = 6
例题2
例题探求
解方程 20-x = 9
例题3
说一说你的想法。
你遇到了什么困难?
例题探求
解方程 20-x = 9
例题3
说一说你的想法。
你遇到了什么困难?
例题探求
规范解答:
20-x = 9
x = 11
解:20-x+x = 9+x
20 = 9+x
9+x = 20
9+x-9 = 20-9
等式两边加上相同的式子,左右两边仍然相等。
+x
+x
例题探求
x = 11是不是正确的答案呢?检验一下。
检验:
方程左边 = 20 - x
= 20 - 11
= 9
=方程右边
所以,x = 11是方程的解。
20-x = 9
小小练习
4 元
x元
1.2元
解:x = 4 – 1.2
x + 1.2= 4
x = 2.8
列方程并解答。
小小练习
8.4 元
x元
x元
x元
解:3x÷3 = 8.4÷3
3x = 8.4
x = 2.8
列方程并解答。
小小练习
(1)解方程4x = 28时,方程两边要同时( )。
(2)解方程x÷5 = 9时,方程两边要同时( ) 。
(3)方程9x = 10.8的解是( ) 。
除以4
乘5
1.2
我会填。
小小练习
(1)x+3.2 = 4.6
解:x+3.2-3.2 = 4.6-3.2
x = 1.4
解:x-1.8+1.8 = 4+1.8
x = 5.8
解下列方程。
(2)x-1.8 = 4
小小练习
(3)15 - x = 2
解: 15-x+x = 2+x
15 = 2+x
2+x = 15
2+x-2 = 15-2
x = 13
解:1.6x÷1.6 = 6.4÷1.6
x = 4
解下列方程。
(4)1.6x = 6.4
小小练习
(5)x÷7 = 0.3
解:x÷7 ×7= 0.3 ×7
x = 2.1
解: 2.1÷x×x = 3×x
2.1 = 3x
3x = 2.1
3x÷3 = 2.1÷3
x = 0.7
解下列方程。
(6)2.1÷x = 3
小小练习
一块长方形菜地的面积是259平方米,这块菜地的长是18.5米,宽是x米。请你列出方程并解答。
解:18.5x = 259
18.5x÷18.5 = 259 ÷18.5
x = 14
答:宽是 14 米。
归纳小结
这节课你们都学会了哪些知识?
解简单的方程
解方程
形如ax = b的方程
解:ax÷a=b÷a
x=b÷a
形如a - x = b的方程
解:a – x + x= b + x
b + x = a
x = a - b
等式的性质2
等式的性质1
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
