3.4.1 相似三角形的判定(1)课件(共13张PPT)
文档属性
| 名称 | 3.4.1 相似三角形的判定(1)课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 262.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
第三章 图形的相似
3.4.1 相似三角形判定的基本定理
复习导入
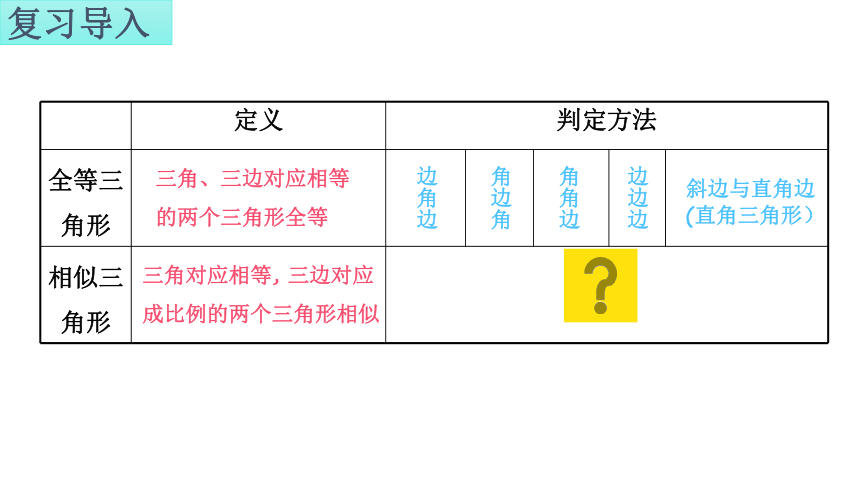
定义 判定方法
全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等, 三边对应成比例的两个三角形相似
角边角
角角边
边边边
边角边
斜边与直角边
(直角三角形)
探究新知
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
(1)△ADE与△ABC的三个角分别相等吗?
(2)对于△ADE与△ABC,它们的边长是否对应成比例?
(3)△ADE与△ABC之间有什么关系?平行移动DE的位置结论还成立吗?
相等
根据平行线分线段成比例的定理,可以知道两个三角形的边长成比例.
关系: △ADE与△ABC相似.
平移DE的位置结论还是成立.
探究新知
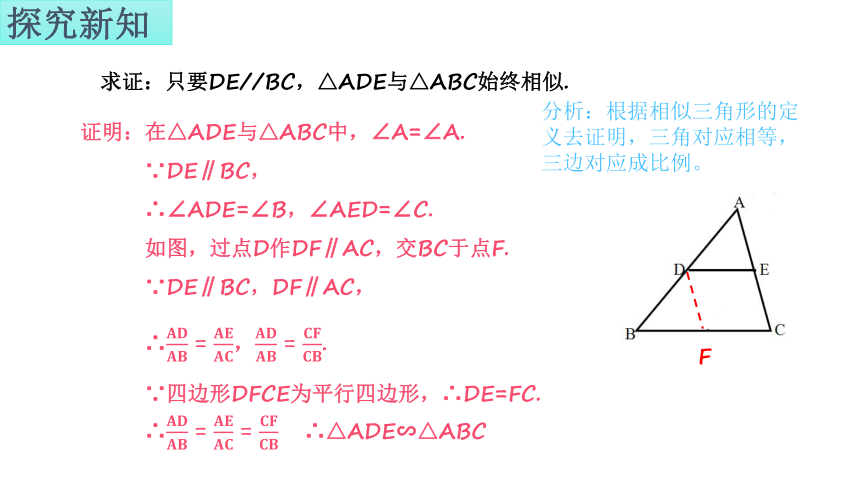
求证:只要DE//BC,△ADE与△ABC始终相似.
证明:在△ADE与△ABC中,∠A=∠A.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
如图,过点D作DF∥AC,交BC于点F.
∵DE∥BC,DF∥AC,
∴,.
∵四边形DFCE为平行四边形,∴DE=FC.
∴ ∴△ADE∽△ABC
F
分析:根据相似三角形的定义去证明,三角对应相等,三边对应成比例。
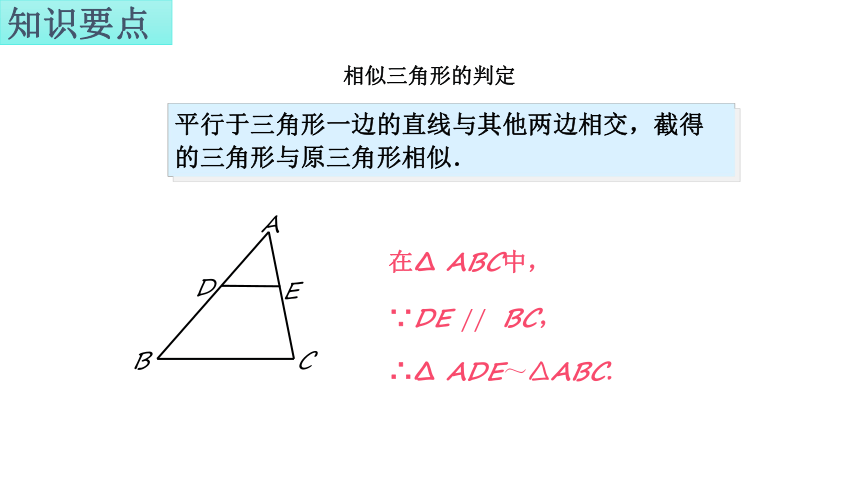
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
在 ABC中,
∵DE BC,
∴ ADEABC.
A
B
C
D
E
相似三角形的判定
知识要点
典例精析
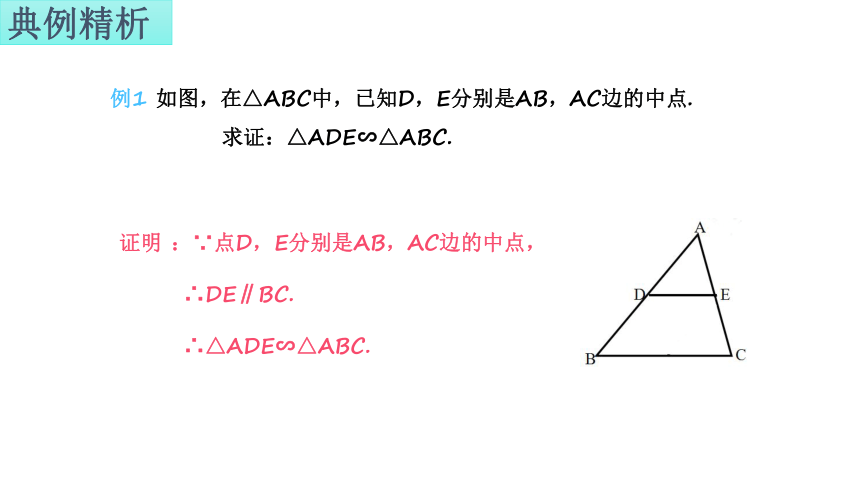
例1 如图,在△ABC中,已知D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
证明 :∵点D,E分别是AB,AC边的中点,
∴DE∥BC.
∴△ADE∽△ABC.
A
B
C
D
E
N
M
已知DE//BC,如果再作MN//DE,共有多少对相似三角形?
△ADE∽△ABC
△AMN∽△ADE
△AMN∽△ABC
相似具有传递性
例2
典例精析
平行线具有传递性
典例精析
例3 如图,点D为△ABC的边AB的中点,过点D作DE∥BC,交边AC于点E.延长DE至点F,使DE=EF. 求证:△CFE∽△ABC.
证明 ∵DE∥BC,点D为△ABC的边AB的中点,
∴AE=CE.
又∵DE=FE,∠AED=∠CEF,
∴△ADE≌△CEF.
∵DE∥BC,
∴△ADE∽△ABC.
∴△CFE∽△ABC.
知识要点
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
∵DE∥BC,
∴△ADE∽△ABC.
D
E
A
C
B
“A”型
“X”型
当堂练习
1. 如图,在Rt△ABC中,∠C=90°.正方形EFCD的三个顶点E,F,D分别在边AB,BC,AC上.已知AC=7.5,BC=5,求正方形的边长.
证明:∵∠C=90°,四边形EFCD是正方形,
∴DE=DC,DE∥CB.
∴△ADE∽△ACB.
解得DE=3.
,即
当堂练习
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
解:四边形AEOF与四边形ABCD相似.
理由:∵OE∥BC,∴△AEO∽△ABC,
∴
∠EAO=∠BAC,
∠AEO=∠B,
∠AOE=∠ACB,
当堂练习
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
∵OF∥CD,∴△AFO∽△ADC,
∴
∠FAO=∠DAC,
∠AFO=∠D,
∠AOF=∠ACD,
∴
∠EAF=∠BAD,
∠AEO=∠B,
∠EOF=∠BCD,
∠AFO=∠D,
∴四边形AEOF与四边形ABCD相似.
课堂小结
相似三角形的判定方法
判定方法:平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似
定义:三个角对应相等,且三条边对应成比例的两个三角形相似.
第三章 图形的相似
3.4.1 相似三角形判定的基本定理
复习导入
定义 判定方法
全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等, 三边对应成比例的两个三角形相似
角边角
角角边
边边边
边角边
斜边与直角边
(直角三角形)
探究新知
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
(1)△ADE与△ABC的三个角分别相等吗?
(2)对于△ADE与△ABC,它们的边长是否对应成比例?
(3)△ADE与△ABC之间有什么关系?平行移动DE的位置结论还成立吗?
相等
根据平行线分线段成比例的定理,可以知道两个三角形的边长成比例.
关系: △ADE与△ABC相似.
平移DE的位置结论还是成立.
探究新知
求证:只要DE//BC,△ADE与△ABC始终相似.
证明:在△ADE与△ABC中,∠A=∠A.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
如图,过点D作DF∥AC,交BC于点F.
∵DE∥BC,DF∥AC,
∴,.
∵四边形DFCE为平行四边形,∴DE=FC.
∴ ∴△ADE∽△ABC
F
分析:根据相似三角形的定义去证明,三角对应相等,三边对应成比例。
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
在 ABC中,
∵DE BC,
∴ ADEABC.
A
B
C
D
E
相似三角形的判定
知识要点
典例精析
例1 如图,在△ABC中,已知D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
证明 :∵点D,E分别是AB,AC边的中点,
∴DE∥BC.
∴△ADE∽△ABC.
A
B
C
D
E
N
M
已知DE//BC,如果再作MN//DE,共有多少对相似三角形?
△ADE∽△ABC
△AMN∽△ADE
△AMN∽△ABC
相似具有传递性
例2
典例精析
平行线具有传递性
典例精析
例3 如图,点D为△ABC的边AB的中点,过点D作DE∥BC,交边AC于点E.延长DE至点F,使DE=EF. 求证:△CFE∽△ABC.
证明 ∵DE∥BC,点D为△ABC的边AB的中点,
∴AE=CE.
又∵DE=FE,∠AED=∠CEF,
∴△ADE≌△CEF.
∵DE∥BC,
∴△ADE∽△ABC.
∴△CFE∽△ABC.
知识要点
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
∵DE∥BC,
∴△ADE∽△ABC.
D
E
A
C
B
“A”型
“X”型
当堂练习
1. 如图,在Rt△ABC中,∠C=90°.正方形EFCD的三个顶点E,F,D分别在边AB,BC,AC上.已知AC=7.5,BC=5,求正方形的边长.
证明:∵∠C=90°,四边形EFCD是正方形,
∴DE=DC,DE∥CB.
∴△ADE∽△ACB.
解得DE=3.
,即
当堂练习
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
解:四边形AEOF与四边形ABCD相似.
理由:∵OE∥BC,∴△AEO∽△ABC,
∴
∠EAO=∠BAC,
∠AEO=∠B,
∠AOE=∠ACB,
当堂练习
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
∵OF∥CD,∴△AFO∽△ADC,
∴
∠FAO=∠DAC,
∠AFO=∠D,
∠AOF=∠ACD,
∴
∠EAF=∠BAD,
∠AEO=∠B,
∠EOF=∠BCD,
∠AFO=∠D,
∴四边形AEOF与四边形ABCD相似.
课堂小结
相似三角形的判定方法
判定方法:平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似
定义:三个角对应相等,且三条边对应成比例的两个三角形相似.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
