24.2.2 直线和圆的位置关系 课件 3课时 (共69张PPT)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 课件 3课时 (共69张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 13:23:39 | ||
图片预览







文档简介
(共69张PPT)
24.2.2 直线和圆的位置关系
第二十四章 圆
人教版九年级数学上
第1课时 直线和圆的位置关系
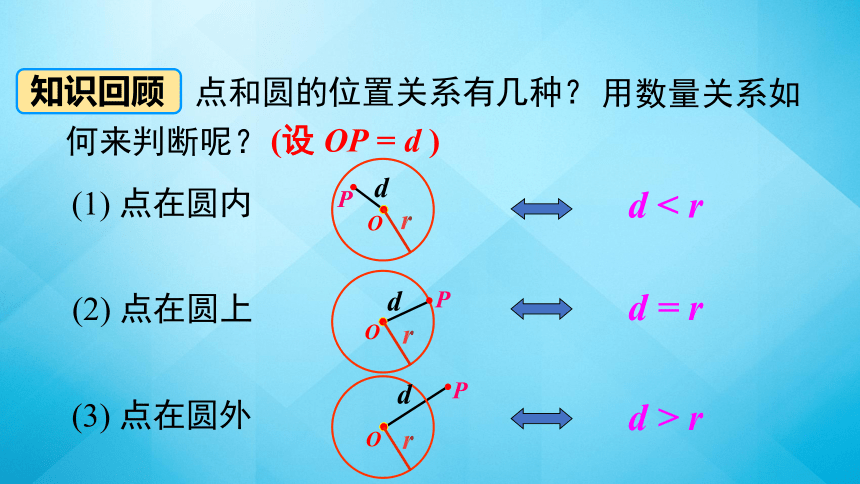
点和圆的位置关系有几种?
d < r
d = r
d > r
用数量关系如何来判断呢?
(设 OP = d )
知识回顾
(1) 点在圆内
(2) 点在圆上
(3) 点在圆外
r
d
r
r
P
P
P
O
O
O
d
d
问题1 如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
用定义判断直线与圆的位置关系
问题2 请同学在纸上画一条直线 l,把圆块的边缘看作圆,在纸上移动圆块,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
l
0
2
●
●
●
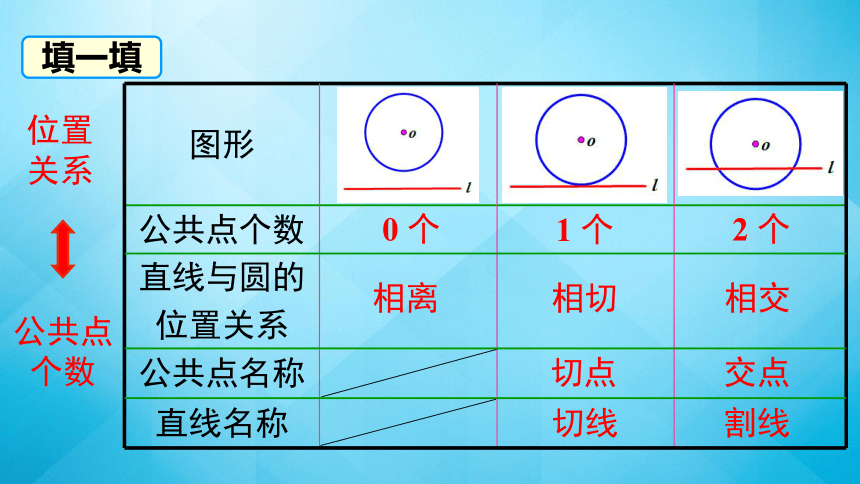
图形
公共点个数
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
位置关系
公共点个数
填一填
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图中的直线 l),这个唯一的公共点叫做切点(如图中的点 A).
A
l
O
知识要点
直线与圆最多有两个公共点. ( )
② 若直线与圆相交,则直线上的点都在圆上. ( )
③ 若 A 是☉O 上一点,则直线 AB 与☉O 相切. ( )
④ 若 C 为☉O 外一点,则过点 C 的直线与☉O 相交或相离. ( )
⑤ 直线 a 和☉O 有公共点,则直线 a 与☉O 相交.( )
√
×
×
×
×
判一判
问题1 刚才同学们用圆块移近直线的过程中,除了发现公共点的个数发生了变化外,还有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点 (A) 到直线 (l ) 的垂线段 (OA) 的长度.
l
A
O
用数量关系判断直线与圆的位置关系
圆心到直线的距离在
发生变化;
首先距离大于半径,
而后距离等于半径,
最后距离小于半径.
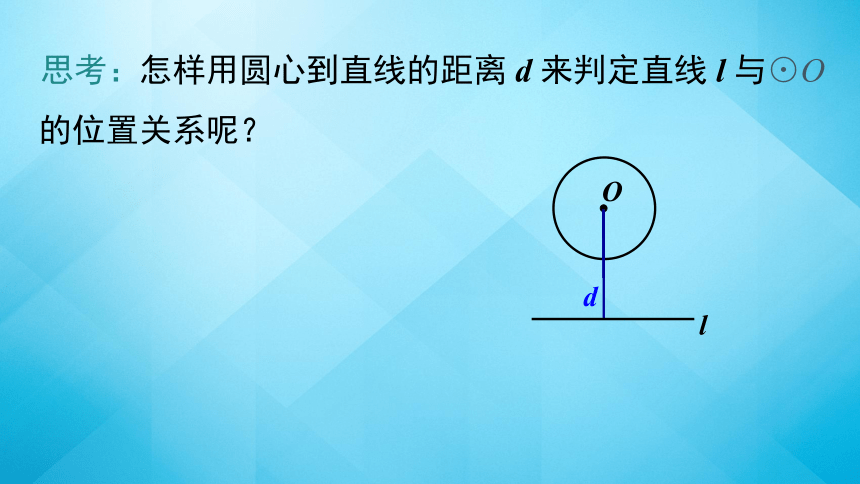
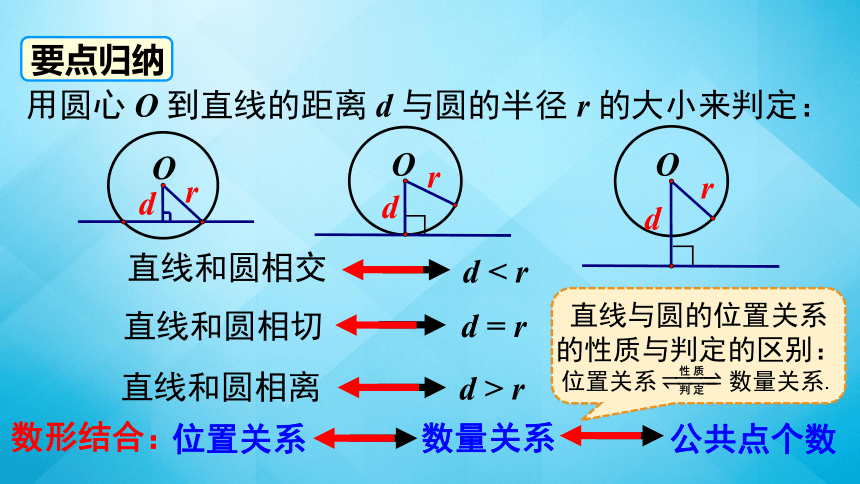
怎样用圆心到直线的距离 d 来判定直线 l 与⊙O 的位置关系呢?
O
思考:
d
l
直线和圆相交
d < r
直线和圆相切
d = r
直线和圆相离
d > r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
用圆心 O 到直线的距离 d 与圆的半径 r 的大小来判定:
O
O
O
直线与圆的位置关系
的性质与判定的区别:
位置关系 数量关系.
公共点个数
要点归纳
1. 已知圆的半径为 6 cm,设直线和圆心的距离为 d.
(3) 若 d = 8 cm,则直线与圆______,直线与圆有____个公共点.
(2) 若 d = 6 cm,则直线与圆______,直线与圆有____个公共点;
(1) 若 d = 4 cm,则直线与圆 ,直线与圆有____个公共点;
相交
相切
相离
2
1
0
练一练
(3) 若 AB 和⊙O 相交,则 .
2. 已知⊙O 的半径为 5 cm,圆心 O 与直线 AB 的距离为 d,根据条件填写 d 的范围:
(1) 若 AB 和⊙O 相离,则 ;
(2) 若 AB 和⊙O 相切,则 ;
d >5 cm
d = 5 cm
0 cm≤d<5 cm
例1 在Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心,r 为半径的圆与直线 AB 有怎样的位置关系?为什么?
(1) r = 2 cm;(2) r = 2.4 cm; (3) r = 3 cm.
B
C
A
4
3
分析:要判定 AB 与⊙C 的位置关系,只要知道圆心 C 到 AB 的距离 d 与 r 的大小关系.已知 r,只需求出 C 到 AB 的距离 d.
D
典例精析
解:过 C 作 CD⊥AB,垂足为 D.
在△ABC 中,
根据三角形的面积公式有
即圆心 C 到 AB 的距离 d = 2.4 cm.
(1) 当 r = 2 cm 时,
有 d > r,
因此⊙C 和 AB 相离;
B
C
A
4
3
D
d
注:斜边上的高等于两直角边长的乘积除以斜边长.
(2) 当 r = 2.4 cm 时,有 d = r,
因此⊙C 和 AB 相切;
B
C
A
4
3
D
d
(3) 当 r = 3 cm 时,有 d < r,
因此⊙C 和 AB 相交.
B
C
A
4
3
D
d
变式题:
1. Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心画圆,当半径 r 为何值时,圆 C 与线段 AB 没有公共点?
当 0 cm<r<2.4 cm 或 r>4 cm 时,
⊙C 与线段 AB 没有公共点.
A
B
C
D
4
5
3
3
2. Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心画圆,当半径 r 为何值时,圆 C 与线段 AB 有一个公共点?当半径 r 为何值时,圆 C 与线段 AB 有两个公共点?
当 r = 2.4 cm 或 3 cm<r≤4 cm 时,⊙C 与线段 AB 有一个公共点;
当 2.4 cm<r≤3 cm 时,⊙C 与线段AB 有两公共点.
A
B
C
D
4
5
3
3
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d 与 r 的数量关系
定义法
性质法
特别提醒:若图中没有 d 要先作出该垂线段
相离:0 个;相切:1 个;相交:2 个
相离:d > r 相切:d = r
相交:d < r
0个:相离;1个:相切;2个:相交
d > r:相离;d = r:相切;d < r:相交
24.2.2 直线和圆的位置关系
第二十四章 圆
人教版九年级数学上
第2课时 切线的判定与性质
知识回顾
图形
公共点个数
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
位置关系
公共点个数
情境引入
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
A
B
C
问题:已知圆 O 上一点 A,怎样根据圆的切线定义过点 A 作圆 O 的切线?
观察:
(1) 圆心 O 到直线 AB 的距离和圆的
半径有什么数量关系
(2)二者位置有什么关系?为什么?
切线的判定定理
O
经过半径的外端并且垂直于这条半径的直线是圆的切线.
OA 为⊙O 的半径
BC⊥OA 于A
BC 为⊙O 的切线
A
B
C
切线的判定定理
应用格式
O
要点归纳
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
下列各直线是不是圆的切线?如果不是,请说明为什么?
(1) 不是,因为没有垂直.
(2) (3) 不是,因为没有经过半径的外端点 A.
判一判
注意
O.
A
O.
A
B
A
O
(1)
(2)
(3)
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r)时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
要点归纳
O
O
例1 如图,线段 AB 是☉O 的直径,直线 AC 与 AB 交于点 A,∠ABC = 45°,且 AB = AC.
求证:AC 是☉O 的切线.
分析:直线 AC 经过半径的一端,因此只要证 OA 垂直于 AC 即可.
证明:∵ AB = AC,∠ABC = 45°,
∴∠ACB =∠ABC = 45°.
∴∠BAC = 180° -∠ABC -∠ACB = 90°,
即 AB⊥AC.
∵ AB 是☉O 的直径,
∴ AC 是☉O 的切线.
A
O
C
B
例2 已知直线 AB 经过 ⊙O 上的点 C,并且 OA = OB,
CA = CB. 求证:直线 AB 是 ⊙O 的切线.
O
B
A
C
证明:连接 OC.
∵ OA = OB,CA = CB,
∴ OC 是等腰△OAB 底边 AB 上的中线.
∴ OC⊥AB.
∵ OC 是 ⊙O 的半径,
∴ AB 是 ⊙O 的切线.
分析:由于 AB 过⊙O 上的点 C,所以连接 OC,只要
证明 AB⊥OC 即可.
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
方法总结
例3 如图,在 Rt△ABC 中,∠ABC = 90°,∠BAC 的平分线交 BC 于 D,以 D 为圆心,DB 长为半径作⊙D.
求证:AC 是⊙O 的切线.
B
C
D
A
E
证明:如图,过 D 作 DE⊥AC 于 E.
∵∠ABC = 90°,∴ DB⊥AB.
又∵ AD 平分∠BAC,DE⊥AC,
∴ DE = DB = r.
∴ AC 是⊙O 的切线.
当未提及直线与圆有公共点时,过圆心作直线的垂线段,证明垂线段等于半径,即可得出已知直线为圆的切线.
方法总结
(1) 有交点,连半径,证垂直;
证切线时辅助线的添加方法
要点归纳
(2) 无交点,作垂直,证半径.
例3
例2
思考:如图,如果直线 l 是⊙O 的切线,点 A 为切点,那么 OA 与 l 垂直吗?
A
l
O
∵直线 l 是⊙O 的切线,A 是切点,
∴直线 l⊥OA.
切线的性质定理
切线的性质
圆的切线垂直于经过切点的半径.
应用格式
(1)假设 AB 与 CD 不垂直,过点 O 作
OM⊥CD,垂足为 M;
理由是:直径 AB 与直线 CD 要么垂直,要么不垂直.
(2)则 OM<OA,即圆心到直线 CD 的
距离小于⊙O 的半径,因此,CD
与⊙O 相交. 这与已知条件“直线
与⊙O 相切”相矛盾;
C
D
B
O
A
(3)所以假设不成立,故 AB 与 CD 垂直.
M
证法:反证法
性质定理的证明
例4 如图,PA 是⊙O 的切线,切点为 A,PO 的延长线交⊙O 于点 B,连接 AB. 若∠B = 25°,求∠P 的度数.
B
O
P
A
解:如图,连接 OA.
∵ PA 是⊙O 的切线,
∵∠AOP = 2∠B = 50°,
∴∠P = 90° - 50° = 40°.
∴∠OAP = 90°.
1. 如图①,在⊙O 中,OA、OB 为半径,直线 MN 与⊙O 相切于点 B. 若∠ABN = 30°,则∠AOB = °.
2. 如图②,AB 为⊙O 的直径,D 为 AB 延长线上一点,DC 与⊙O 相切于点 C,∠DAC = 30°. 若⊙O 的半径长 1 cm,则 OD = cm.
60
练一练
图①
图②
利用切线的性质解题时,常需作辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
方法总结
例5 如图,△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D.求证:AC 是⊙O 的切线.
分析:判定切线,无切点,则作垂直(OE),证半径(OE = OD);由 AB 与⊙O相切于点 D,得 OD⊥AB;再根据等腰三角形的性质以及角平分线的性质,即可得出结论.
E
B
O
C
D
A
证明:如图,连接 OD,OA,过 O 作 OE ⊥AC 于 E.
∵ ⊙O 与 AB 相切于 D,∴ OD⊥AB.
又∵△ABC 为等腰三角形,O 是 BC 的中点,
∴ AO 平分∠BAC.
∴ OE = OD.
∵ OD 是⊙O 的半径,
∴ 点 O 到 AC 的距离等于⊙O 的半径.
∴ AC 是⊙O 的切线.
E
B
O
C
D
A
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1) 经过圆心且垂直于切线的直线必经过切点;
(2) 经过切点且垂直于切线的直线必经过圆心.
要点归纳
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d = r,则相切
经过圆的半径的外端且垂直于这条半径的直线是圆的切线
切线的性质
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
有 1 个公共点
d = r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线添加方法:
见切线,连切点,得垂直.
24.2.2 直线和圆的位置关系
第二十四章 圆
人教版九年级数学上
第3课时 切线长定理及三角形的内切圆
情境引入
同学们玩过抖空竹和悠悠球吗?在空竹和悠悠球旋转的那一瞬间,你能从中抽象出什么样数学图形?
问题1 上节课我们学习了过圆上一点作已知圆的切线(如下图所示),如果点 P 是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?
切线长定理及应用
互动探究
P
O
B
A
O.
P
A
B
P
1. 切线长的定义:
经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长.
A
O
① 切线是直线,不能度量;
② 切线长是线段的长,这条线段的两个端点分别是
圆外一点和切点,可以度量.
2. 切线长与切线的区别在哪里?
知识要点
问题2 PA 为☉O 的一条切线,沿着直线 PO 对折,设圆上与点 A 重合的点为 B.
OB 是☉O 的一条半径吗?
PB 是☉O 的切线吗?
(利用图形轴对称性解释)
PA、PB 有何关系?
∠APO 和∠BPO 有何关系?
O
P
A
B
切线长定理:
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
PA、PB 分别切 ☉O 于 A、B
PA = PB
∠OPA = ∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新
的方法.
注意
要点归纳
B
P
O
A
O.
P
已知:如图,PA、PB 是☉O 的两条切线,A、B 为切点.
求证:PA = PB,∠APO =∠BPO.
证明:∵ PA、PB 是☉O 的两条切线,
∵ OA = OB,OP = OP,
∴ Rt△OAP≌Rt△OBP(HL).
∴ PA = PB,∠APO =∠BPO.
推理验证
A
B
∴ OA⊥PA,OB⊥PB.
若连接两切点 A、B,AB 交 OP 于点 M. 你又能得出
什么新的结论 请给出证明.
解:OP 垂直平分 AB.
证明:∵ PA,PB 是 ⊙O 的切线,点 A,B 是切点,
∴ PA = PB,∠OPA =∠OPB.
∴ △PAB 是等腰三角形,
PM 为顶角的平分线.
∴ OP 垂直平分 AB.
M
想一想:
O
P
A
B
例1 已知:如图,四边形 ABCD 的边 AB、BC、CD、
DA 与 ⊙O 分别相切于点 E、F、G、H.
求证:AB + CD = AD + BC.
证明:∵ AB、BC、CD、DA 与 ⊙O 分别相切于点 E、F、G、H,
·
A
B
C
D
O
E
F
G
H
∴ AE = AH,BE = BF,
CG = CF,DG = DH.
∴ AE + BE + CG + DG = AH + BF + CF + DH,
即 AB + CD = AD + BC.
典例精析
变式训练
如图,四边形 ABCD 是☉O 的外切四边形,且 AB = 10,CD = 15,则四边形 ABCD 的周长为______.
50
·
A
B
C
D
O
例4 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为 30° 的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径. 若三角板与圆相切且测得 PA =
5 cm,求铁环的半径.
O
B
C
解析:取圆的圆心为O,连接 OA,OP,由切线性质知△OPA为直角三角形,从而在 Rt△OPA 中由勾股定理易求得半径.
在 Rt△OPA 中,PA=5,∠POA=30°,
又∵∠BAC=60°,∴∠PAO=∠BAO=60°.
即铁环的半径为
∴ OA = 2PA = 10.
解:设铁环的圆心为 O,连接 OP、OA.
∴ OP⊥AP,∠PAO=∠BAO.
O
B
C
5
∵ AP、AB 为 ⊙O 的切线,
∴ OP =
∴∠POA=30°.
切线长定理包括线段相等和角相等两个结论,解题时应有选择地应用,它是证明线段相等、角相等以及垂直关系的重要依据.
方法归纳
B
P
O
A
PA、PB 是 ☉O 的两条切线,A,B 是切点,OA = 3.
(1)若 AP = 4,则 OP = ;
(2)若∠BPA = 60°,则 OP = .
5
6
练一练
小明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
三角形的内切圆及作法
互动探究
问题1 如果最大圆存在,它与三角形三边应有怎样的位置关系?
O
O
O
O
最大的圆与三角形三边都相切
问题2 如何求作一个圆,使它与三角形的三边都相切?
(1) 如果半径为 r 的☉I 与△ABC 的三边都相切,那么
圆心 I 应满足什么条件?
(2) 在△ABC 的内部,如何找到满足条件的圆心 I 呢?
圆心 I 到三角形三边的距离相等,都等于 r.
为什么呢?
三角形三条角平分线交于一点,这一点到三角形三边的距离相等.
三角形角平分线的这个性质,你还记得吗?
圆心 I 应是三角形的三条角平分线的交点.
已知:△ABC.
求作:和△ABC 的各边都相切的圆 O.
做一做
M
N
D
作法:
1. 作∠ABC 和∠ACB 的平分线
BM 和 CN,交点为 O.
2. 过点 O 作OD⊥BC,垂足为 D.
3. 以O为圆心,OD为半径作圆O.
☉O 就是所求的圆.
A
B
C
O
1. 与三角形三边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做这个三角形的内心.
3. 这个三角形叫做这个圆的外切三角形.
B
A
C
I
☉I 是△ABC 的内切圆,
点 I 是△ABC 的内心,
△ABC 是☉I 的外切三角形.
知识要点
三角形的内心的性质
问题1 如图,☉O 是△ABC 的内切圆,那么 AO、BO、CO 有什么特点?
互动探究
AO、BO、CO 分别平分∠CAB、∠ABC、∠BCA.
B
A
C
O
B
A
C
O
问题2 如图,☉O 是△ABC 的内切圆,过点 O 分别作 AB、AC、BC 的垂线,垂足分别为 E、F、G,那么线段 OE、OF、OG 之间有什么数量关系?
E
F
G
解:OE = OF = OG.
知识要点
三角形内心的性质
三角形的内心是三角形三条角平分线的交点.
三角形的内心到三角形三边的距离相等.
AI、BI、CI 分别平分∠CAB、∠ABC、∠BCA,IE = IF = IG.
B
A
C
I
E
F
G
例3 如图,△ABC 中,∠B = 43°,∠C = 61°,点 I 是△ABC 的内心,求∠BIC 的度数.
解:连接 IB,IC.
A
B
C
I
∵ 点 I 是△ABC 的内心,
∴ BI,CI 分别平分∠ABC,∠ACB.
在△IBC 中,
例4 △ABC 的内切圆 ☉O 与 BC、CA、AB 分别相切于点 D、E、F,且 AB = 13 cm,BC = 14 cm,CA = 9 cm,求 AF、BD、CE 的长.
想一想:图中你能找出哪些相等的线段?理由是什么?
B
A
C
E
D
F
O
解:
设 AF = x cm,则 AE = x cm.
∴ CE = CD = AC - AE = 9 - x (cm),
BF = BD = AB - AF = 13 - x (cm).
由 BD + CD = BC,可得
(13 - x) + (9 - x) = 14,
∴ AF = 4 cm,BD = 9 cm,CE = 5 cm.
方法小结:解决本题的关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程求解.
解得 x = 4.
B
A
C
E
D
F
O
比一比
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边垂直平分线的交点
1.OA = OB = OC;
2.不一定在三角形内部
三角形三条
角平分线的
交点
1.到三边距离相等;
2. AO、BO、CO 分别平分∠BAC、∠ABC、∠ACB;
3.在三角形内部
A
B
O
C
A
B
C
O
切线长
切线长定理
作用
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程
应用
重要结论
内心的概念及性质
图形的轴对称性
原理
谢谢观看
24.2.2 直线和圆的位置关系
第二十四章 圆
人教版九年级数学上
第1课时 直线和圆的位置关系
点和圆的位置关系有几种?
d < r
d = r
d > r
用数量关系如何来判断呢?
(设 OP = d )
知识回顾
(1) 点在圆内
(2) 点在圆上
(3) 点在圆外
r
d
r
r
P
P
P
O
O
O
d
d
问题1 如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
用定义判断直线与圆的位置关系
问题2 请同学在纸上画一条直线 l,把圆块的边缘看作圆,在纸上移动圆块,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
l
0
2
●
●
●
图形
公共点个数
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
位置关系
公共点个数
填一填
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图中的直线 l),这个唯一的公共点叫做切点(如图中的点 A).
A
l
O
知识要点
直线与圆最多有两个公共点. ( )
② 若直线与圆相交,则直线上的点都在圆上. ( )
③ 若 A 是☉O 上一点,则直线 AB 与☉O 相切. ( )
④ 若 C 为☉O 外一点,则过点 C 的直线与☉O 相交或相离. ( )
⑤ 直线 a 和☉O 有公共点,则直线 a 与☉O 相交.( )
√
×
×
×
×
判一判
问题1 刚才同学们用圆块移近直线的过程中,除了发现公共点的个数发生了变化外,还有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点 (A) 到直线 (l ) 的垂线段 (OA) 的长度.
l
A
O
用数量关系判断直线与圆的位置关系
圆心到直线的距离在
发生变化;
首先距离大于半径,
而后距离等于半径,
最后距离小于半径.
怎样用圆心到直线的距离 d 来判定直线 l 与⊙O 的位置关系呢?
O
思考:
d
l
直线和圆相交
d < r
直线和圆相切
d = r
直线和圆相离
d > r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
用圆心 O 到直线的距离 d 与圆的半径 r 的大小来判定:
O
O
O
直线与圆的位置关系
的性质与判定的区别:
位置关系 数量关系.
公共点个数
要点归纳
1. 已知圆的半径为 6 cm,设直线和圆心的距离为 d.
(3) 若 d = 8 cm,则直线与圆______,直线与圆有____个公共点.
(2) 若 d = 6 cm,则直线与圆______,直线与圆有____个公共点;
(1) 若 d = 4 cm,则直线与圆 ,直线与圆有____个公共点;
相交
相切
相离
2
1
0
练一练
(3) 若 AB 和⊙O 相交,则 .
2. 已知⊙O 的半径为 5 cm,圆心 O 与直线 AB 的距离为 d,根据条件填写 d 的范围:
(1) 若 AB 和⊙O 相离,则 ;
(2) 若 AB 和⊙O 相切,则 ;
d >5 cm
d = 5 cm
0 cm≤d<5 cm
例1 在Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心,r 为半径的圆与直线 AB 有怎样的位置关系?为什么?
(1) r = 2 cm;(2) r = 2.4 cm; (3) r = 3 cm.
B
C
A
4
3
分析:要判定 AB 与⊙C 的位置关系,只要知道圆心 C 到 AB 的距离 d 与 r 的大小关系.已知 r,只需求出 C 到 AB 的距离 d.
D
典例精析
解:过 C 作 CD⊥AB,垂足为 D.
在△ABC 中,
根据三角形的面积公式有
即圆心 C 到 AB 的距离 d = 2.4 cm.
(1) 当 r = 2 cm 时,
有 d > r,
因此⊙C 和 AB 相离;
B
C
A
4
3
D
d
注:斜边上的高等于两直角边长的乘积除以斜边长.
(2) 当 r = 2.4 cm 时,有 d = r,
因此⊙C 和 AB 相切;
B
C
A
4
3
D
d
(3) 当 r = 3 cm 时,有 d < r,
因此⊙C 和 AB 相交.
B
C
A
4
3
D
d
变式题:
1. Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心画圆,当半径 r 为何值时,圆 C 与线段 AB 没有公共点?
当 0 cm<r<2.4 cm 或 r>4 cm 时,
⊙C 与线段 AB 没有公共点.
A
B
C
D
4
5
3
3
2. Rt△ABC 中,∠C = 90°,AC = 3 cm,BC = 4 cm,以 C 为圆心画圆,当半径 r 为何值时,圆 C 与线段 AB 有一个公共点?当半径 r 为何值时,圆 C 与线段 AB 有两个公共点?
当 r = 2.4 cm 或 3 cm<r≤4 cm 时,⊙C 与线段 AB 有一个公共点;
当 2.4 cm<r≤3 cm 时,⊙C 与线段AB 有两公共点.
A
B
C
D
4
5
3
3
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d 与 r 的数量关系
定义法
性质法
特别提醒:若图中没有 d 要先作出该垂线段
相离:0 个;相切:1 个;相交:2 个
相离:d > r 相切:d = r
相交:d < r
0个:相离;1个:相切;2个:相交
d > r:相离;d = r:相切;d < r:相交
24.2.2 直线和圆的位置关系
第二十四章 圆
人教版九年级数学上
第2课时 切线的判定与性质
知识回顾
图形
公共点个数
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
位置关系
公共点个数
情境引入
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
A
B
C
问题:已知圆 O 上一点 A,怎样根据圆的切线定义过点 A 作圆 O 的切线?
观察:
(1) 圆心 O 到直线 AB 的距离和圆的
半径有什么数量关系
(2)二者位置有什么关系?为什么?
切线的判定定理
O
经过半径的外端并且垂直于这条半径的直线是圆的切线.
OA 为⊙O 的半径
BC⊥OA 于A
BC 为⊙O 的切线
A
B
C
切线的判定定理
应用格式
O
要点归纳
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
下列各直线是不是圆的切线?如果不是,请说明为什么?
(1) 不是,因为没有垂直.
(2) (3) 不是,因为没有经过半径的外端点 A.
判一判
注意
O.
A
O.
A
B
A
O
(1)
(2)
(3)
判断一条直线是一个圆的切线有三个方法:
1. 定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2. 数量关系法:圆心到这条直线的距离等于半径(即 d = r)时,直线与圆相切;
3. 判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
要点归纳
O
O
例1 如图,线段 AB 是☉O 的直径,直线 AC 与 AB 交于点 A,∠ABC = 45°,且 AB = AC.
求证:AC 是☉O 的切线.
分析:直线 AC 经过半径的一端,因此只要证 OA 垂直于 AC 即可.
证明:∵ AB = AC,∠ABC = 45°,
∴∠ACB =∠ABC = 45°.
∴∠BAC = 180° -∠ABC -∠ACB = 90°,
即 AB⊥AC.
∵ AB 是☉O 的直径,
∴ AC 是☉O 的切线.
A
O
C
B
例2 已知直线 AB 经过 ⊙O 上的点 C,并且 OA = OB,
CA = CB. 求证:直线 AB 是 ⊙O 的切线.
O
B
A
C
证明:连接 OC.
∵ OA = OB,CA = CB,
∴ OC 是等腰△OAB 底边 AB 上的中线.
∴ OC⊥AB.
∵ OC 是 ⊙O 的半径,
∴ AB 是 ⊙O 的切线.
分析:由于 AB 过⊙O 上的点 C,所以连接 OC,只要
证明 AB⊥OC 即可.
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
方法总结
例3 如图,在 Rt△ABC 中,∠ABC = 90°,∠BAC 的平分线交 BC 于 D,以 D 为圆心,DB 长为半径作⊙D.
求证:AC 是⊙O 的切线.
B
C
D
A
E
证明:如图,过 D 作 DE⊥AC 于 E.
∵∠ABC = 90°,∴ DB⊥AB.
又∵ AD 平分∠BAC,DE⊥AC,
∴ DE = DB = r.
∴ AC 是⊙O 的切线.
当未提及直线与圆有公共点时,过圆心作直线的垂线段,证明垂线段等于半径,即可得出已知直线为圆的切线.
方法总结
(1) 有交点,连半径,证垂直;
证切线时辅助线的添加方法
要点归纳
(2) 无交点,作垂直,证半径.
例3
例2
思考:如图,如果直线 l 是⊙O 的切线,点 A 为切点,那么 OA 与 l 垂直吗?
A
l
O
∵直线 l 是⊙O 的切线,A 是切点,
∴直线 l⊥OA.
切线的性质定理
切线的性质
圆的切线垂直于经过切点的半径.
应用格式
(1)假设 AB 与 CD 不垂直,过点 O 作
OM⊥CD,垂足为 M;
理由是:直径 AB 与直线 CD 要么垂直,要么不垂直.
(2)则 OM<OA,即圆心到直线 CD 的
距离小于⊙O 的半径,因此,CD
与⊙O 相交. 这与已知条件“直线
与⊙O 相切”相矛盾;
C
D
B
O
A
(3)所以假设不成立,故 AB 与 CD 垂直.
M
证法:反证法
性质定理的证明
例4 如图,PA 是⊙O 的切线,切点为 A,PO 的延长线交⊙O 于点 B,连接 AB. 若∠B = 25°,求∠P 的度数.
B
O
P
A
解:如图,连接 OA.
∵ PA 是⊙O 的切线,
∵∠AOP = 2∠B = 50°,
∴∠P = 90° - 50° = 40°.
∴∠OAP = 90°.
1. 如图①,在⊙O 中,OA、OB 为半径,直线 MN 与⊙O 相切于点 B. 若∠ABN = 30°,则∠AOB = °.
2. 如图②,AB 为⊙O 的直径,D 为 AB 延长线上一点,DC 与⊙O 相切于点 C,∠DAC = 30°. 若⊙O 的半径长 1 cm,则 OD = cm.
60
练一练
图①
图②
利用切线的性质解题时,常需作辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
方法总结
例5 如图,△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D.求证:AC 是⊙O 的切线.
分析:判定切线,无切点,则作垂直(OE),证半径(OE = OD);由 AB 与⊙O相切于点 D,得 OD⊥AB;再根据等腰三角形的性质以及角平分线的性质,即可得出结论.
E
B
O
C
D
A
证明:如图,连接 OD,OA,过 O 作 OE ⊥AC 于 E.
∵ ⊙O 与 AB 相切于 D,∴ OD⊥AB.
又∵△ABC 为等腰三角形,O 是 BC 的中点,
∴ AO 平分∠BAC.
∴ OE = OD.
∵ OD 是⊙O 的半径,
∴ 点 O 到 AC 的距离等于⊙O 的半径.
∴ AC 是⊙O 的切线.
E
B
O
C
D
A
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1) 经过圆心且垂直于切线的直线必经过切点;
(2) 经过切点且垂直于切线的直线必经过圆心.
要点归纳
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d = r,则相切
经过圆的半径的外端且垂直于这条半径的直线是圆的切线
切线的性质
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
有 1 个公共点
d = r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线添加方法:
见切线,连切点,得垂直.
24.2.2 直线和圆的位置关系
第二十四章 圆
人教版九年级数学上
第3课时 切线长定理及三角形的内切圆
情境引入
同学们玩过抖空竹和悠悠球吗?在空竹和悠悠球旋转的那一瞬间,你能从中抽象出什么样数学图形?
问题1 上节课我们学习了过圆上一点作已知圆的切线(如下图所示),如果点 P 是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?
切线长定理及应用
互动探究
P
O
B
A
O.
P
A
B
P
1. 切线长的定义:
经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长.
A
O
① 切线是直线,不能度量;
② 切线长是线段的长,这条线段的两个端点分别是
圆外一点和切点,可以度量.
2. 切线长与切线的区别在哪里?
知识要点
问题2 PA 为☉O 的一条切线,沿着直线 PO 对折,设圆上与点 A 重合的点为 B.
OB 是☉O 的一条半径吗?
PB 是☉O 的切线吗?
(利用图形轴对称性解释)
PA、PB 有何关系?
∠APO 和∠BPO 有何关系?
O
P
A
B
切线长定理:
过圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
PA、PB 分别切 ☉O 于 A、B
PA = PB
∠OPA = ∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新
的方法.
注意
要点归纳
B
P
O
A
O.
P
已知:如图,PA、PB 是☉O 的两条切线,A、B 为切点.
求证:PA = PB,∠APO =∠BPO.
证明:∵ PA、PB 是☉O 的两条切线,
∵ OA = OB,OP = OP,
∴ Rt△OAP≌Rt△OBP(HL).
∴ PA = PB,∠APO =∠BPO.
推理验证
A
B
∴ OA⊥PA,OB⊥PB.
若连接两切点 A、B,AB 交 OP 于点 M. 你又能得出
什么新的结论 请给出证明.
解:OP 垂直平分 AB.
证明:∵ PA,PB 是 ⊙O 的切线,点 A,B 是切点,
∴ PA = PB,∠OPA =∠OPB.
∴ △PAB 是等腰三角形,
PM 为顶角的平分线.
∴ OP 垂直平分 AB.
M
想一想:
O
P
A
B
例1 已知:如图,四边形 ABCD 的边 AB、BC、CD、
DA 与 ⊙O 分别相切于点 E、F、G、H.
求证:AB + CD = AD + BC.
证明:∵ AB、BC、CD、DA 与 ⊙O 分别相切于点 E、F、G、H,
·
A
B
C
D
O
E
F
G
H
∴ AE = AH,BE = BF,
CG = CF,DG = DH.
∴ AE + BE + CG + DG = AH + BF + CF + DH,
即 AB + CD = AD + BC.
典例精析
变式训练
如图,四边形 ABCD 是☉O 的外切四边形,且 AB = 10,CD = 15,则四边形 ABCD 的周长为______.
50
·
A
B
C
D
O
例4 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为 30° 的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径. 若三角板与圆相切且测得 PA =
5 cm,求铁环的半径.
O
B
C
解析:取圆的圆心为O,连接 OA,OP,由切线性质知△OPA为直角三角形,从而在 Rt△OPA 中由勾股定理易求得半径.
在 Rt△OPA 中,PA=5,∠POA=30°,
又∵∠BAC=60°,∴∠PAO=∠BAO=60°.
即铁环的半径为
∴ OA = 2PA = 10.
解:设铁环的圆心为 O,连接 OP、OA.
∴ OP⊥AP,∠PAO=∠BAO.
O
B
C
5
∵ AP、AB 为 ⊙O 的切线,
∴ OP =
∴∠POA=30°.
切线长定理包括线段相等和角相等两个结论,解题时应有选择地应用,它是证明线段相等、角相等以及垂直关系的重要依据.
方法归纳
B
P
O
A
PA、PB 是 ☉O 的两条切线,A,B 是切点,OA = 3.
(1)若 AP = 4,则 OP = ;
(2)若∠BPA = 60°,则 OP = .
5
6
练一练
小明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
三角形的内切圆及作法
互动探究
问题1 如果最大圆存在,它与三角形三边应有怎样的位置关系?
O
O
O
O
最大的圆与三角形三边都相切
问题2 如何求作一个圆,使它与三角形的三边都相切?
(1) 如果半径为 r 的☉I 与△ABC 的三边都相切,那么
圆心 I 应满足什么条件?
(2) 在△ABC 的内部,如何找到满足条件的圆心 I 呢?
圆心 I 到三角形三边的距离相等,都等于 r.
为什么呢?
三角形三条角平分线交于一点,这一点到三角形三边的距离相等.
三角形角平分线的这个性质,你还记得吗?
圆心 I 应是三角形的三条角平分线的交点.
已知:△ABC.
求作:和△ABC 的各边都相切的圆 O.
做一做
M
N
D
作法:
1. 作∠ABC 和∠ACB 的平分线
BM 和 CN,交点为 O.
2. 过点 O 作OD⊥BC,垂足为 D.
3. 以O为圆心,OD为半径作圆O.
☉O 就是所求的圆.
A
B
C
O
1. 与三角形三边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做这个三角形的内心.
3. 这个三角形叫做这个圆的外切三角形.
B
A
C
I
☉I 是△ABC 的内切圆,
点 I 是△ABC 的内心,
△ABC 是☉I 的外切三角形.
知识要点
三角形的内心的性质
问题1 如图,☉O 是△ABC 的内切圆,那么 AO、BO、CO 有什么特点?
互动探究
AO、BO、CO 分别平分∠CAB、∠ABC、∠BCA.
B
A
C
O
B
A
C
O
问题2 如图,☉O 是△ABC 的内切圆,过点 O 分别作 AB、AC、BC 的垂线,垂足分别为 E、F、G,那么线段 OE、OF、OG 之间有什么数量关系?
E
F
G
解:OE = OF = OG.
知识要点
三角形内心的性质
三角形的内心是三角形三条角平分线的交点.
三角形的内心到三角形三边的距离相等.
AI、BI、CI 分别平分∠CAB、∠ABC、∠BCA,IE = IF = IG.
B
A
C
I
E
F
G
例3 如图,△ABC 中,∠B = 43°,∠C = 61°,点 I 是△ABC 的内心,求∠BIC 的度数.
解:连接 IB,IC.
A
B
C
I
∵ 点 I 是△ABC 的内心,
∴ BI,CI 分别平分∠ABC,∠ACB.
在△IBC 中,
例4 △ABC 的内切圆 ☉O 与 BC、CA、AB 分别相切于点 D、E、F,且 AB = 13 cm,BC = 14 cm,CA = 9 cm,求 AF、BD、CE 的长.
想一想:图中你能找出哪些相等的线段?理由是什么?
B
A
C
E
D
F
O
解:
设 AF = x cm,则 AE = x cm.
∴ CE = CD = AC - AE = 9 - x (cm),
BF = BD = AB - AF = 13 - x (cm).
由 BD + CD = BC,可得
(13 - x) + (9 - x) = 14,
∴ AF = 4 cm,BD = 9 cm,CE = 5 cm.
方法小结:解决本题的关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程求解.
解得 x = 4.
B
A
C
E
D
F
O
比一比
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边垂直平分线的交点
1.OA = OB = OC;
2.不一定在三角形内部
三角形三条
角平分线的
交点
1.到三边距离相等;
2. AO、BO、CO 分别平分∠BAC、∠ABC、∠ACB;
3.在三角形内部
A
B
O
C
A
B
C
O
切线长
切线长定理
作用
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程
应用
重要结论
内心的概念及性质
图形的轴对称性
原理
谢谢观看
同课章节目录
