人教版小数六年级上册 4.1 比的意义和比的基本性质 课件
文档属性
| 名称 | 人教版小数六年级上册 4.1 比的意义和比的基本性质 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 16:27:29 | ||
图片预览





文档简介
(共24张PPT)
比的意义和比
的基本性质
人教版 六年级上册
例题探求
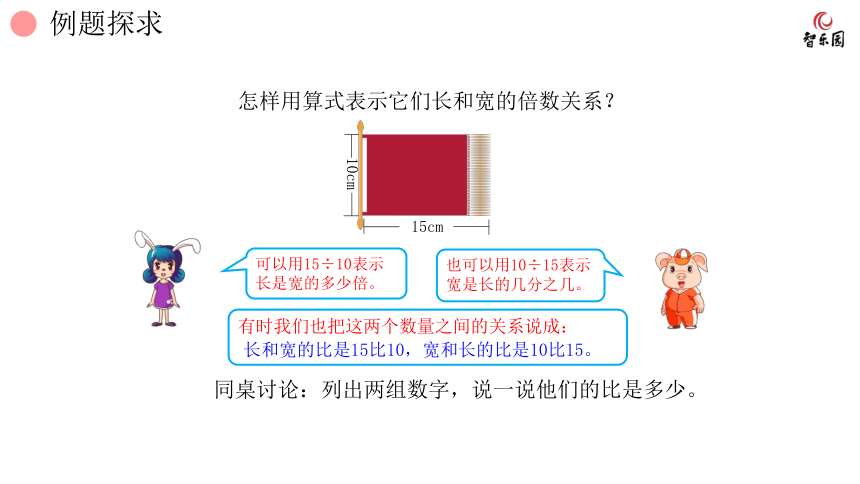
15cm
10cm
也可以用10÷15表示宽是长的几分之几。
可以用15÷10表示长是宽的多少倍。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15。
同桌讨论:列出两组数字,说一说他们的比是多少。
怎样用算式表示它们长和宽的倍数关系?
例题探求
时间
路程
怎样用算式表示飞船进入轨道后平均每分钟飞行多少千米?
速度可以用路程÷时间表示。
我们也可以用比来表示路程和时间的关系:
路程和时间的比是:42252比90。
42252÷90
“神舟”五号进入运行轨道后,在距地350km的高空做圆周运动,平均90分钟绕地球一周,大约运行42252km.
例题探求
仔细观察算式,你发现了什么?
15÷10
10÷15
42252÷90
15比10
10比15
42252比90
两个数的比表示两个数相除。
试着用自己的话说一说你的发现。
例题探求
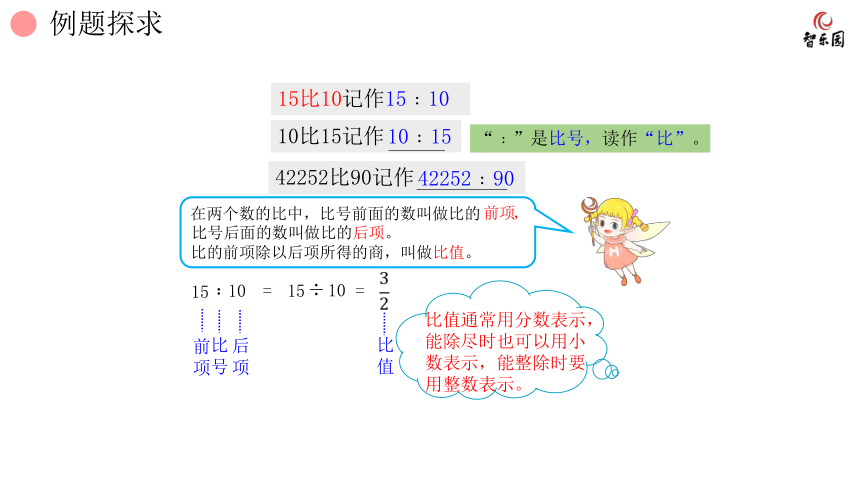
15比10记作15﹕10
10比15记作
42252比90记作
“﹕”是比号,读作“比”。
在两个数的比中,比号前面的数叫做比的 ,
15
10
:
15
10
=
÷
=
前项
比号
后项
比值
比值通常用分数表示,能除尽时也可以用小数表示,能整除时要用整数表示。
10﹕15
42252﹕90
比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
前项
例题探求
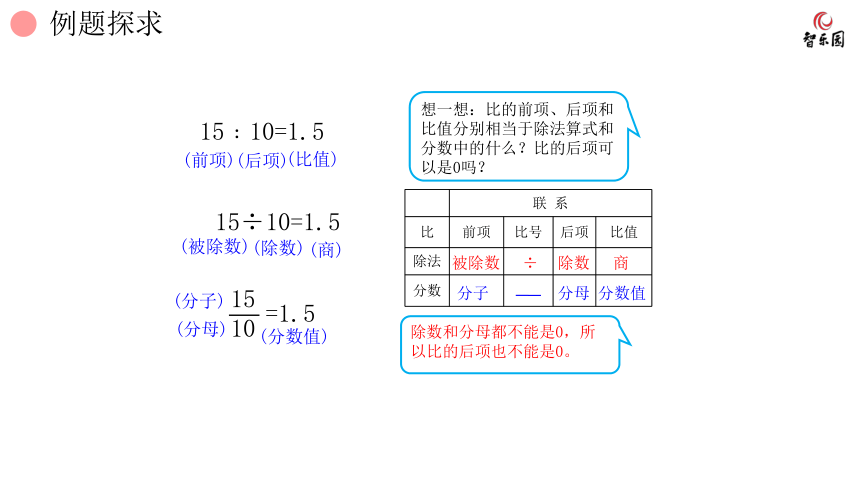
15﹕10=1.5
15÷10=1.5
=1.5
15
10
(前项)
(后项)
(比值)
(分母)
(商)
(被除数)
(除数)
(分子)
(分数值)
想一想:比的前项、后项和比值分别相当于除法算式和分数中的什么?比的后项可以是0吗?
联 系 比 前项 比号 后项 比值
除法
分数
被除数
÷
商
除数
分子
分母
分数值
除数和分母都不能是0,所以比的后项也不能是0。
例题探求
联系比和除法、分数的关系,想一想:在比中有什么样的规律?
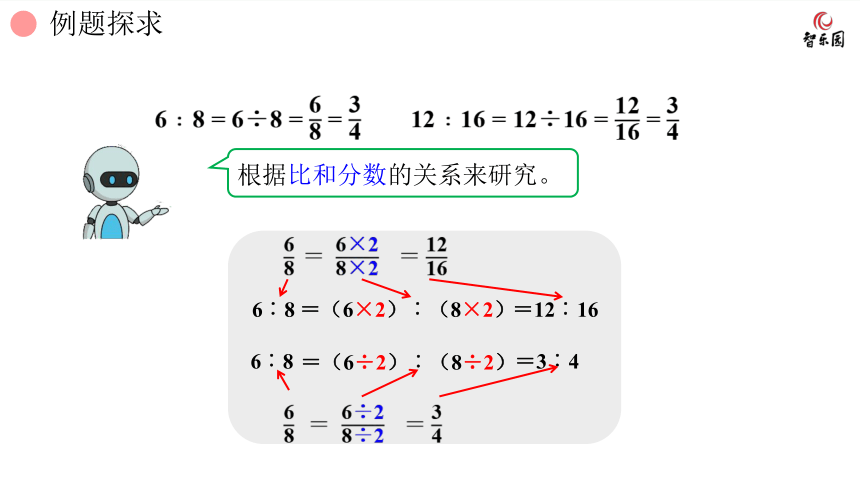
6﹕8 = 6÷8 = =
12﹕16 = 12÷16 = =
例题探求
6÷8=(6×2)÷(8×2)=12÷16
6÷8=(6÷2)÷(8÷2)=3÷4
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
6﹕8 = 6÷8 = =
12﹕16 = 12÷16 = =
利用比和除法的关系来研究。
例题探求
6﹕8 = 6÷8 = =
12﹕16 = 12÷16 = =
根据比和分数的关系来研究。
= =
= =
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
例题探求
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
这叫作比的基本性质。
例题探求
=( )∶( )
(180÷ )(120÷ )
想:5是15和10的什么数?为什么要除以5?
(15÷5)∶(10÷5)
180∶120 =
60
60
3
2
180和120要同时除以几?
(1)神舟五号搭载了两面联合国旗帜,一面长15cm,宽10cm(前面展示过),另一面长180cm,宽120cm。这两面联合国旗帜长和宽的最简单的整数比分别是多少?
15∶10 =
= 3∶2
5是15和10的最大公因数,利用比的基本性质化简。
例题探求
能同时把比的前项和后项化为整数的数。
比的前项和后项分母的最小公倍数。
=(×18)∶(×18)
=3∶4
比的前项和后项同时乘相同的数(0除外),比值不变。
∶
∶
0.75∶2
例题探求
0.75∶2
=(0.75×100)∶(2× )
100
比的前项和后项再同时除以它们的最大公因数。
把比的前项化为整数。
=75∶200
=(75÷25)∶(200÷25)
=3∶8
例题探求
=(×18)∶(×18)
=3∶4
∶
0.75∶2
=75∶200
=(75÷25)∶(200÷25)
=3∶8
当一个比的前项或后项不是整数时,怎样把它化成最简单的整数比?
利用比的基本性质,把非整数的比转化成整数比,再化简。
小小练习
6﹕8=6÷8=
小敏和小亮在文具店买同样的练习本。小敏买了6本,共花了12元。小亮买了8本,共花了16元。小敏和小亮买的练习本数之比是( )﹕( ),比值是( );花的钱数是之比是( )﹕( ),比值是( )。
6
8
12
16
12﹕16=12÷16=
小小练习
3﹕( )=24
除数=被除数÷商
后项=前项÷比值
3÷24=0.125
0.125
( )﹕8=0.5
被除数=除数x商
前项=后项x比值
8×0.5=4
4
小小练习
填空题。
1.三好学生占全班人数的,三好学生与全班人数的比是( )。
2.一本书读了55页,还有45页没有读, 已读的页数与总页数的比是( ),比值是( )。
1﹕7
55﹕100
小小练习
判断题。
1.比的前项和后项可以是任意数。 ( )
2.不同类的两个数量之间的关系也可以用比表示。
( )
3.6﹕5读作6比5,也可以读作五分之六。 ( )
×
√
√
小小练习
你还记得商不变的规律和分数的基本性质吗?
在除法里,被除数与除数同时扩大或缩小相同的倍数,商大小不变。
分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
小小练习
欢欢和乐乐分别从各自的家去游乐场,小明走的
路程是小红的,而小明花的时间是小红的,
小明和小红的速度比是多少?
思路引导:
小明走的路程是小红的 小明和小红所走的路程比是8﹕9;
小明花的时间是小红的 小明和小红所用的时间比是2﹕3;
小小练习
(8÷2)﹕(9÷3)=4﹕3
答:小明和小红的速度比是4﹕3
根据“路程÷时间=速度”可以得到小明和
小红的速度比是(8÷2)﹕(9÷3)。
欢欢和乐乐分别从各自的家去游乐场,小明走的
路程是小红的,而小明花的时间是小红的,
小明和小红的速度比是多少?
归纳小结
这节课你们都学会了哪些知识?
两个数量之间的关系可以用两个数的比来表示。
在两个数的比中,“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项,比的前项除以后项所得的商叫做比值。
比的前项,后项和比值分别相当于除法算式中的:被除数,除数和商;分别相当于分数中的:分子、分母和分数值。比的后项不能是0。
归纳小结
这节课你们都学会了哪些知识?
比的基本性质:比的前项和后项同时乘或除以相同的数
(0除外),比值不变。
用途:化简比(把比化简成最简单的整数比)。
整数比化简方法:除以最大公因数。
分数比化简方法:先化成整数比,或用求比值的方法化简。
小数比化简方法:先化成整数比,再化简。
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
比的意义和比
的基本性质
人教版 六年级上册
例题探求
15cm
10cm
也可以用10÷15表示宽是长的几分之几。
可以用15÷10表示长是宽的多少倍。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15。
同桌讨论:列出两组数字,说一说他们的比是多少。
怎样用算式表示它们长和宽的倍数关系?
例题探求
时间
路程
怎样用算式表示飞船进入轨道后平均每分钟飞行多少千米?
速度可以用路程÷时间表示。
我们也可以用比来表示路程和时间的关系:
路程和时间的比是:42252比90。
42252÷90
“神舟”五号进入运行轨道后,在距地350km的高空做圆周运动,平均90分钟绕地球一周,大约运行42252km.
例题探求
仔细观察算式,你发现了什么?
15÷10
10÷15
42252÷90
15比10
10比15
42252比90
两个数的比表示两个数相除。
试着用自己的话说一说你的发现。
例题探求
15比10记作15﹕10
10比15记作
42252比90记作
“﹕”是比号,读作“比”。
在两个数的比中,比号前面的数叫做比的 ,
15
10
:
15
10
=
÷
=
前项
比号
后项
比值
比值通常用分数表示,能除尽时也可以用小数表示,能整除时要用整数表示。
10﹕15
42252﹕90
比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
前项
例题探求
15﹕10=1.5
15÷10=1.5
=1.5
15
10
(前项)
(后项)
(比值)
(分母)
(商)
(被除数)
(除数)
(分子)
(分数值)
想一想:比的前项、后项和比值分别相当于除法算式和分数中的什么?比的后项可以是0吗?
联 系 比 前项 比号 后项 比值
除法
分数
被除数
÷
商
除数
分子
分母
分数值
除数和分母都不能是0,所以比的后项也不能是0。
例题探求
联系比和除法、分数的关系,想一想:在比中有什么样的规律?
6﹕8 = 6÷8 = =
12﹕16 = 12÷16 = =
例题探求
6÷8=(6×2)÷(8×2)=12÷16
6÷8=(6÷2)÷(8÷2)=3÷4
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
6﹕8 = 6÷8 = =
12﹕16 = 12÷16 = =
利用比和除法的关系来研究。
例题探求
6﹕8 = 6÷8 = =
12﹕16 = 12÷16 = =
根据比和分数的关系来研究。
= =
= =
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
例题探求
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
这叫作比的基本性质。
例题探求
=( )∶( )
(180÷ )(120÷ )
想:5是15和10的什么数?为什么要除以5?
(15÷5)∶(10÷5)
180∶120 =
60
60
3
2
180和120要同时除以几?
(1)神舟五号搭载了两面联合国旗帜,一面长15cm,宽10cm(前面展示过),另一面长180cm,宽120cm。这两面联合国旗帜长和宽的最简单的整数比分别是多少?
15∶10 =
= 3∶2
5是15和10的最大公因数,利用比的基本性质化简。
例题探求
能同时把比的前项和后项化为整数的数。
比的前项和后项分母的最小公倍数。
=(×18)∶(×18)
=3∶4
比的前项和后项同时乘相同的数(0除外),比值不变。
∶
∶
0.75∶2
例题探求
0.75∶2
=(0.75×100)∶(2× )
100
比的前项和后项再同时除以它们的最大公因数。
把比的前项化为整数。
=75∶200
=(75÷25)∶(200÷25)
=3∶8
例题探求
=(×18)∶(×18)
=3∶4
∶
0.75∶2
=75∶200
=(75÷25)∶(200÷25)
=3∶8
当一个比的前项或后项不是整数时,怎样把它化成最简单的整数比?
利用比的基本性质,把非整数的比转化成整数比,再化简。
小小练习
6﹕8=6÷8=
小敏和小亮在文具店买同样的练习本。小敏买了6本,共花了12元。小亮买了8本,共花了16元。小敏和小亮买的练习本数之比是( )﹕( ),比值是( );花的钱数是之比是( )﹕( ),比值是( )。
6
8
12
16
12﹕16=12÷16=
小小练习
3﹕( )=24
除数=被除数÷商
后项=前项÷比值
3÷24=0.125
0.125
( )﹕8=0.5
被除数=除数x商
前项=后项x比值
8×0.5=4
4
小小练习
填空题。
1.三好学生占全班人数的,三好学生与全班人数的比是( )。
2.一本书读了55页,还有45页没有读, 已读的页数与总页数的比是( ),比值是( )。
1﹕7
55﹕100
小小练习
判断题。
1.比的前项和后项可以是任意数。 ( )
2.不同类的两个数量之间的关系也可以用比表示。
( )
3.6﹕5读作6比5,也可以读作五分之六。 ( )
×
√
√
小小练习
你还记得商不变的规律和分数的基本性质吗?
在除法里,被除数与除数同时扩大或缩小相同的倍数,商大小不变。
分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
小小练习
欢欢和乐乐分别从各自的家去游乐场,小明走的
路程是小红的,而小明花的时间是小红的,
小明和小红的速度比是多少?
思路引导:
小明走的路程是小红的 小明和小红所走的路程比是8﹕9;
小明花的时间是小红的 小明和小红所用的时间比是2﹕3;
小小练习
(8÷2)﹕(9÷3)=4﹕3
答:小明和小红的速度比是4﹕3
根据“路程÷时间=速度”可以得到小明和
小红的速度比是(8÷2)﹕(9÷3)。
欢欢和乐乐分别从各自的家去游乐场,小明走的
路程是小红的,而小明花的时间是小红的,
小明和小红的速度比是多少?
归纳小结
这节课你们都学会了哪些知识?
两个数量之间的关系可以用两个数的比来表示。
在两个数的比中,“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项,比的前项除以后项所得的商叫做比值。
比的前项,后项和比值分别相当于除法算式中的:被除数,除数和商;分别相当于分数中的:分子、分母和分数值。比的后项不能是0。
归纳小结
这节课你们都学会了哪些知识?
比的基本性质:比的前项和后项同时乘或除以相同的数
(0除外),比值不变。
用途:化简比(把比化简成最简单的整数比)。
整数比化简方法:除以最大公因数。
分数比化简方法:先化成整数比,或用求比值的方法化简。
小数比化简方法:先化成整数比,再化简。
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
