人教版小数六年级上册 3.7 分数除法--解决问题(三) 课件
文档属性
| 名称 | 人教版小数六年级上册 3.7 分数除法--解决问题(三) 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 16:27:29 | ||
图片预览


文档简介
(共28张PPT)
解决问题(三)
人教版 六年级上册
情境导入
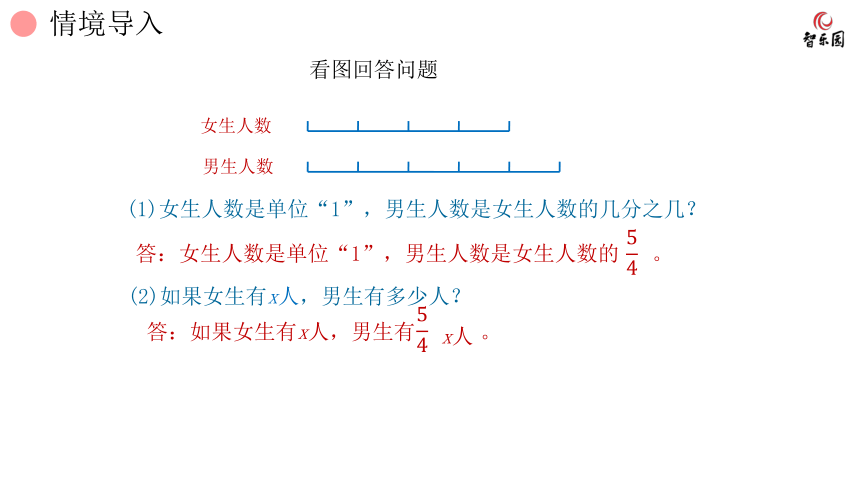
看图回答问题
女生人数
男生人数
(1)女生人数是单位“1”,男生人数是女生人数的几分之几?
答:女生人数是单位“1”,男生人数是女生人数的 。
x人
答:如果女生有x人,男生有 。
(2)如果女生有x人,男生有多少人?
情境导入
根据信息,找出数量关系式。
(1)体积相等的冰的质量比水的质量少 。
(2)今年比去年增产 。
水的质量×(1- )=冰的质量
去年的产量×(1+ )=今年的产量
例题探求
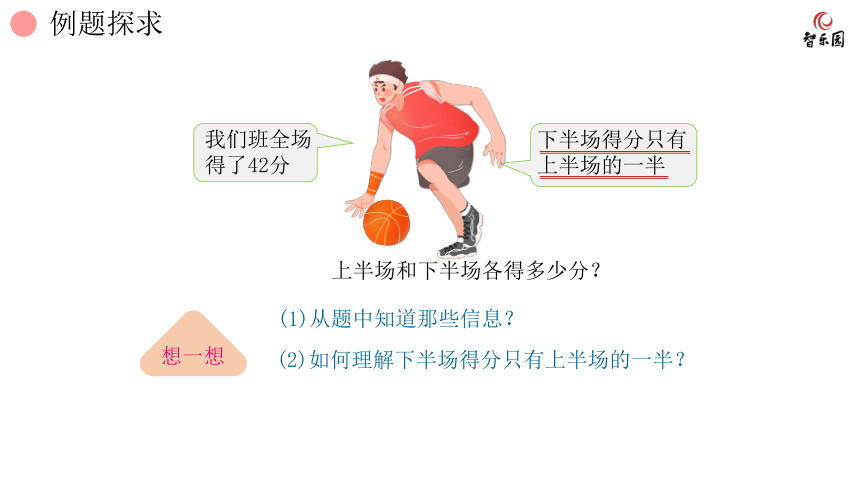
上半场和下半场各得多少分?
(1)从题中知道那些信息?
想一想
(2)如何理解下半场得分只有上半场的一半?
我们班全场得了42分
下半场得分只有上半场的一半
例题探求
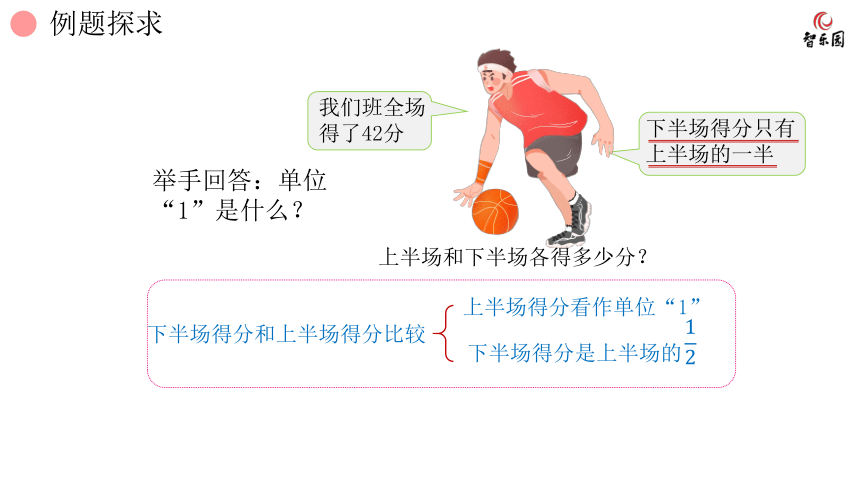
上半场和下半场各得多少分?
上半场得分看作单位“1”
下半场得分和上半场得分比较
下半场得分是上半场的
举手回答:单位“1”是什么?
我们班全场得了42分
下半场得分只有上半场的一半
例题探求
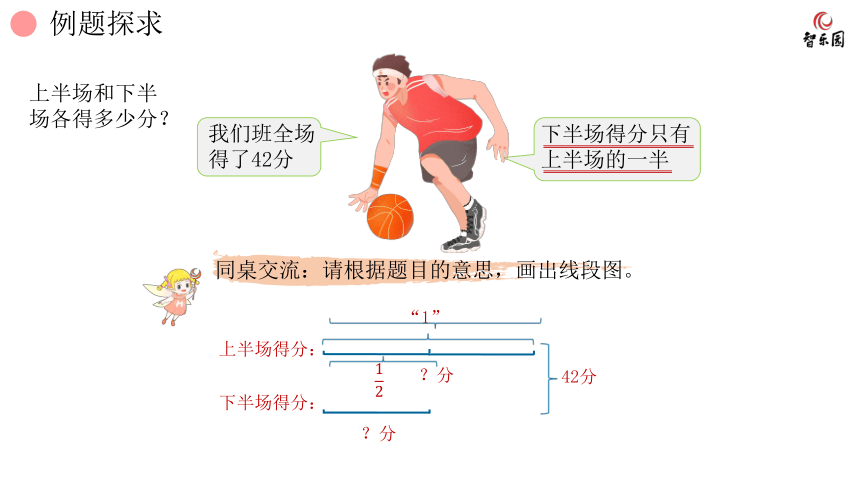
同桌交流:请根据题目的意思,画出线段图。
上半场和下半场各得多少分?
上半场得分:
下半场得分:
“1”
?分
?分
42分
我们班全场得了42分
下半场得分只有上半场的一半
例题探求
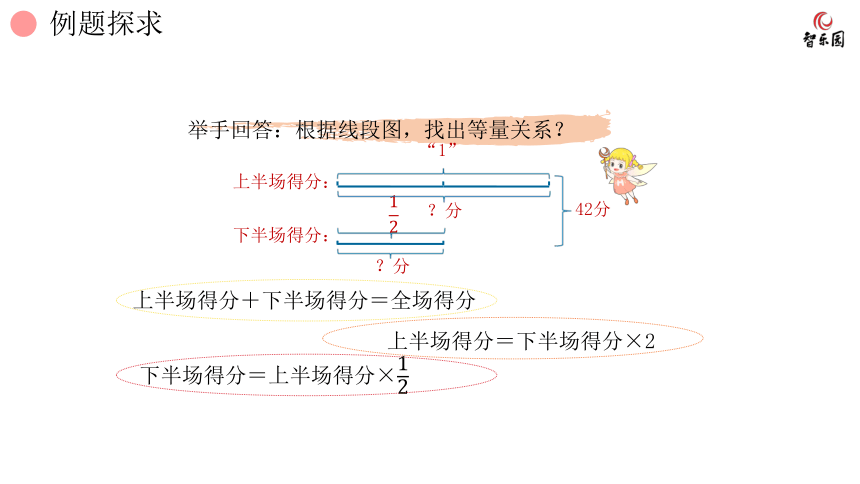
举手回答:根据线段图,找出等量关系?
上半场得分:
下半场得分:
“1”
?分
?分
42分
上半场得分+下半场得分=全场得分
下半场得分=上半场得分×
上半场得分=下半场得分×2
例题探求
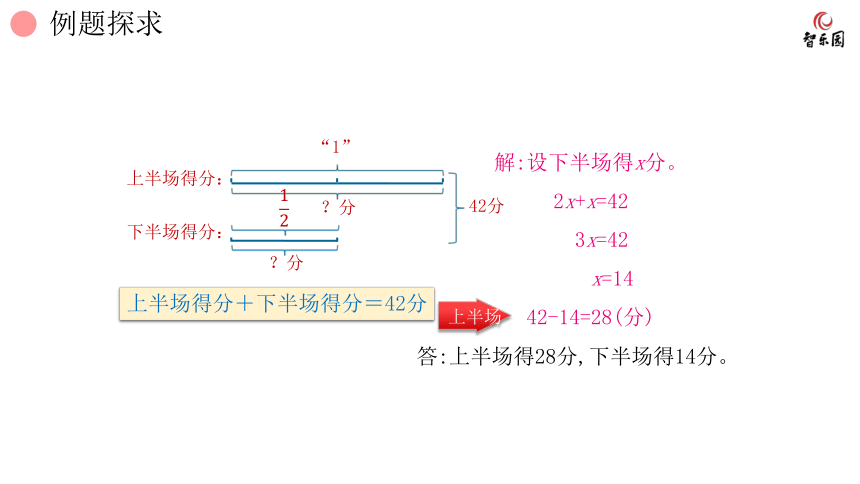
解:设下半场得x分。
2x+x=42
3x=42
x=14
42-14=28(分)
答:上半场得28分,下半场得14分。
上半场得分:
下半场得分:
“1”
?分
?分
42分
上半场得分+下半场得分=42分
上半场
例题探求
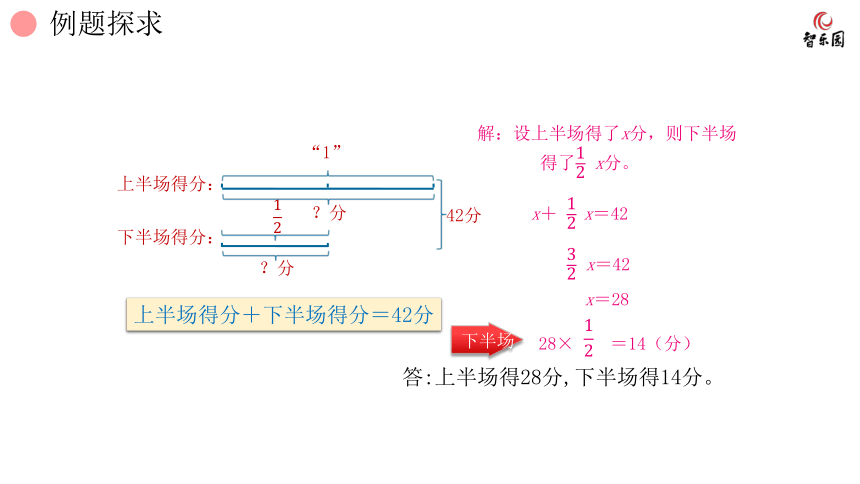
上半场得分+下半场得分=42分
答:上半场得28分,下半场得14分。
上半场得分:
下半场得分:
“1”
?分
?分
42分
解:设上半场得了x分,则下半场
得了 x分。
x+ x=42
x=42
x=28
下半场
28× =14(分)
例题探求
上半场得分+下半场得分=42分
依据题意画出了相同的线段图,找到了相同的等量关系,为什么同学们列出的方程不一样呢?
解:设下半场得x分。
2x+x=42
3x=42
x=14
42-14=28(分)
解:设上半场得了x分,则下半场得了 x分。
x+ x=42
x=42
x=28
28×=14(分)
先设哪个量为未知数,再利用两个量的数量关系,用代数式表示出另一个量。
例题探求
全场总得分÷全场总得分占上半场得分的几分之几=上半场得分
答:上半场得28分,下半场得14分。
上半场得分:
下半场得分:
“1”
?分
?分
42分
下半场
上半场
例题探求
一设
如果设其中一个数是x,根据两个数的“倍分”(倍数和分数)关系用含有x的式子表示另一个数;
二列
根据“两个数的和(或差)等于已知量”列方程;
三解
解方程求出x的值。
已知两个数的和(或差)及这两个数的倍数关系,求这两个数的方法
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
(1)从题中知道了什么?要解决的问题是什么?
(2)要解决问题,需要知道哪些信息?
阅读与理解
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
知道了两队单独修完这条路所用的时间。
“合修”是什么意思?
合修就是一起修。同时开始,同时结束。修完为止。
可是不知道这条道路有多长,怎么求天数呢?
例题探求
如果知道两队单独修完所需要的时间和这条道路的长度,就能求出各队的工作效率。
要求“两队合修,多少天能修完”,是求两队合作的工作时间。合作时间一定小于任何一队单独完成的时间。
分析与解答
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
例题探求
条件不够,
怎么解答?
这条路的总长度?
两队合修,每天修多少千米?
一队每天
修的长度
二队每天
修的长度
?
只要知道这条路的总长度……
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
假设这条路长_______千米。
18km
18km
18km
1.5km
1km
(1.5+1)km
甲队每天修:______________
乙队每天修:______________
两队合修,每天修:______________
两队合修,需要多少天:______________
18
18÷12=1.5(千米)
18÷18=1(千米)
1.5+1=2.5(千米)
18÷2.5=7.2(天)
甲:
乙:
合:
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
甲队每天修:______________
乙队每天修:______________
两队合修,每天修:__________________
两队合修,需要多少天:_______________
30km
30km
30km
km
km
(+)km
30÷12=(千米)
30÷18=(千米)
+=+ =(千米)
30÷==7.2(天)
假设这条路长_______千米。
30
甲:
乙:
合:
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
甲队每天修:______________
乙队每天修:______________
两队合修,每天修:______________
两队合修,需要多少天:
也可以假设这条道路的长度是“1”。
“1”
“1”
“1”
km
km
(+ )km
1÷12=
1÷18 =
+ =
1÷(+ )
=_______
=7.2(天)
1÷
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
怎样才能知道以上的解决方法是否正确?把你的想法写下来,和同学交流一下。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成“1”,很简便。
答:如果两队合修,7.2天可以修完。
回顾与反思
可以用假设的具体数量来检验,也可以用抽象“1”的方法检验。
小小练习
(2)设每个乒乓球拍的价格是x元,则乒乓球的价格是( ),列方程为( )。
(1)设乒乓球的价格是x元,则每个乒乓球拍的价格是( ),列方程( )。
14x
x+2×14x=580
2x+ =580
x
某商店每个乒乓球拍的价格是每个乒乓球的14倍,张老师买了一些乒乓球和球拍共花了580元。
x
小小练习
某电视厂去年全年生产电视机108万台,其中上半年产量是下半年的。这个电视机厂去年上半年和下半年的产量分别是多少万台?
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
小小练习
上半年产量+下半年产量=全年产量
解:设下半年生产x万台,则上半年生产 x万台。
x+ x=108
x =108
x=60
答:这个电视机厂去年上半年的产量是48万台,下半年的产量是60万台。
60 × =48(万台)
上半年
某电视厂去年全年生产电视机108万台,其中上半年产量是下半年的。这个电视机厂去年上半年和下半年的产量分别是多少万台?
小小练习
自助餐厅有一袋大米,第一周用去这袋大米的,
第二周用去这袋大米的,还剩下70千克,这袋
大米重多少千克?
解:设这袋大米x千克。
(1- - ) x =70
x =200
答:这袋大米重200千克。
小小练习
一批货物,只用甲车运,6次能运完;只用乙车运,3次能运完。如果两辆车一起运,多少次能运完这批货物?
1÷(+)
=1÷
=2(次)
答:如果两辆车一起运,2次能运完这批货物。
小小练习
挖一条水渠,王伯伯每天能挖整条水渠的,李叔叔每天能挖整条水渠的。两人合作,几天能挖完?
答:两人合作,12天能挖完。
1÷(+)
=1÷
=12(天)
归纳小结
这节课你们都学会了哪些知识?
含有两个未知量的实际问题
用方程解:找到题中数量间的等量关系,设单位“1”的量为x,列出方程。
算术法解:
已知量÷已知量占单位“1”的几分之几=单位“1”。
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
解决问题(三)
人教版 六年级上册
情境导入
看图回答问题
女生人数
男生人数
(1)女生人数是单位“1”,男生人数是女生人数的几分之几?
答:女生人数是单位“1”,男生人数是女生人数的 。
x人
答:如果女生有x人,男生有 。
(2)如果女生有x人,男生有多少人?
情境导入
根据信息,找出数量关系式。
(1)体积相等的冰的质量比水的质量少 。
(2)今年比去年增产 。
水的质量×(1- )=冰的质量
去年的产量×(1+ )=今年的产量
例题探求
上半场和下半场各得多少分?
(1)从题中知道那些信息?
想一想
(2)如何理解下半场得分只有上半场的一半?
我们班全场得了42分
下半场得分只有上半场的一半
例题探求
上半场和下半场各得多少分?
上半场得分看作单位“1”
下半场得分和上半场得分比较
下半场得分是上半场的
举手回答:单位“1”是什么?
我们班全场得了42分
下半场得分只有上半场的一半
例题探求
同桌交流:请根据题目的意思,画出线段图。
上半场和下半场各得多少分?
上半场得分:
下半场得分:
“1”
?分
?分
42分
我们班全场得了42分
下半场得分只有上半场的一半
例题探求
举手回答:根据线段图,找出等量关系?
上半场得分:
下半场得分:
“1”
?分
?分
42分
上半场得分+下半场得分=全场得分
下半场得分=上半场得分×
上半场得分=下半场得分×2
例题探求
解:设下半场得x分。
2x+x=42
3x=42
x=14
42-14=28(分)
答:上半场得28分,下半场得14分。
上半场得分:
下半场得分:
“1”
?分
?分
42分
上半场得分+下半场得分=42分
上半场
例题探求
上半场得分+下半场得分=42分
答:上半场得28分,下半场得14分。
上半场得分:
下半场得分:
“1”
?分
?分
42分
解:设上半场得了x分,则下半场
得了 x分。
x+ x=42
x=42
x=28
下半场
28× =14(分)
例题探求
上半场得分+下半场得分=42分
依据题意画出了相同的线段图,找到了相同的等量关系,为什么同学们列出的方程不一样呢?
解:设下半场得x分。
2x+x=42
3x=42
x=14
42-14=28(分)
解:设上半场得了x分,则下半场得了 x分。
x+ x=42
x=42
x=28
28×=14(分)
先设哪个量为未知数,再利用两个量的数量关系,用代数式表示出另一个量。
例题探求
全场总得分÷全场总得分占上半场得分的几分之几=上半场得分
答:上半场得28分,下半场得14分。
上半场得分:
下半场得分:
“1”
?分
?分
42分
下半场
上半场
例题探求
一设
如果设其中一个数是x,根据两个数的“倍分”(倍数和分数)关系用含有x的式子表示另一个数;
二列
根据“两个数的和(或差)等于已知量”列方程;
三解
解方程求出x的值。
已知两个数的和(或差)及这两个数的倍数关系,求这两个数的方法
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
(1)从题中知道了什么?要解决的问题是什么?
(2)要解决问题,需要知道哪些信息?
阅读与理解
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
知道了两队单独修完这条路所用的时间。
“合修”是什么意思?
合修就是一起修。同时开始,同时结束。修完为止。
可是不知道这条道路有多长,怎么求天数呢?
例题探求
如果知道两队单独修完所需要的时间和这条道路的长度,就能求出各队的工作效率。
要求“两队合修,多少天能修完”,是求两队合作的工作时间。合作时间一定小于任何一队单独完成的时间。
分析与解答
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
例题探求
条件不够,
怎么解答?
这条路的总长度?
两队合修,每天修多少千米?
一队每天
修的长度
二队每天
修的长度
?
只要知道这条路的总长度……
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
假设这条路长_______千米。
18km
18km
18km
1.5km
1km
(1.5+1)km
甲队每天修:______________
乙队每天修:______________
两队合修,每天修:______________
两队合修,需要多少天:______________
18
18÷12=1.5(千米)
18÷18=1(千米)
1.5+1=2.5(千米)
18÷2.5=7.2(天)
甲:
乙:
合:
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
甲队每天修:______________
乙队每天修:______________
两队合修,每天修:__________________
两队合修,需要多少天:_______________
30km
30km
30km
km
km
(+)km
30÷12=(千米)
30÷18=(千米)
+=+ =(千米)
30÷==7.2(天)
假设这条路长_______千米。
30
甲:
乙:
合:
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
甲队每天修:______________
乙队每天修:______________
两队合修,每天修:______________
两队合修,需要多少天:
也可以假设这条道路的长度是“1”。
“1”
“1”
“1”
km
km
(+ )km
1÷12=
1÷18 =
+ =
1÷(+ )
=_______
=7.2(天)
1÷
例题探求
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
怎样才能知道以上的解决方法是否正确?把你的想法写下来,和同学交流一下。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成“1”,很简便。
答:如果两队合修,7.2天可以修完。
回顾与反思
可以用假设的具体数量来检验,也可以用抽象“1”的方法检验。
小小练习
(2)设每个乒乓球拍的价格是x元,则乒乓球的价格是( ),列方程为( )。
(1)设乒乓球的价格是x元,则每个乒乓球拍的价格是( ),列方程( )。
14x
x+2×14x=580
2x+ =580
x
某商店每个乒乓球拍的价格是每个乒乓球的14倍,张老师买了一些乒乓球和球拍共花了580元。
x
小小练习
某电视厂去年全年生产电视机108万台,其中上半年产量是下半年的。这个电视机厂去年上半年和下半年的产量分别是多少万台?
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
小小练习
上半年产量+下半年产量=全年产量
解:设下半年生产x万台,则上半年生产 x万台。
x+ x=108
x =108
x=60
答:这个电视机厂去年上半年的产量是48万台,下半年的产量是60万台。
60 × =48(万台)
上半年
某电视厂去年全年生产电视机108万台,其中上半年产量是下半年的。这个电视机厂去年上半年和下半年的产量分别是多少万台?
小小练习
自助餐厅有一袋大米,第一周用去这袋大米的,
第二周用去这袋大米的,还剩下70千克,这袋
大米重多少千克?
解:设这袋大米x千克。
(1- - ) x =70
x =200
答:这袋大米重200千克。
小小练习
一批货物,只用甲车运,6次能运完;只用乙车运,3次能运完。如果两辆车一起运,多少次能运完这批货物?
1÷(+)
=1÷
=2(次)
答:如果两辆车一起运,2次能运完这批货物。
小小练习
挖一条水渠,王伯伯每天能挖整条水渠的,李叔叔每天能挖整条水渠的。两人合作,几天能挖完?
答:两人合作,12天能挖完。
1÷(+)
=1÷
=12(天)
归纳小结
这节课你们都学会了哪些知识?
含有两个未知量的实际问题
用方程解:找到题中数量间的等量关系,设单位“1”的量为x,列出方程。
算术法解:
已知量÷已知量占单位“1”的几分之几=单位“1”。
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
