人教版小数六年级上册 6.6 百分数(一) 解决问题 课件
文档属性
| 名称 | 人教版小数六年级上册 6.6 百分数(一) 解决问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 16:27:29 | ||
图片预览





文档简介
(共16张PPT)
解决问题
人教版 六年级上册
情境导入
(一)只列式不计算:
1.180米增加20%是多少米?
2 .图书馆有故事类书籍2000册,历史类书籍1500册,历史类书籍比故事类书籍少百分之几?
180×(1+20%)
(2000-1500)÷2000
情境导入
(二)找出下列题目中表示单位“1”的量:
1 .连环画的本数是故事数本数的37.5%;
2 .果园里苹果树的棵树比梨树多50%;
3 .冰箱售价1800元,十一商场搞活动,降了10%。
例题探求
4月价格=
方法一:假设此商
品3月价格是100元。
3月价格
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
×
(1-20%)
单位“1”
4月价格
×
(1+20%)
4月价格:
100
×
(1-20%)
=100×0.8
=80(元)
5月价格:
80
×
(1+20%)
=80×1.2
=96(元)
5月价格=
探 究
例题探求
5月价格与
3月比较
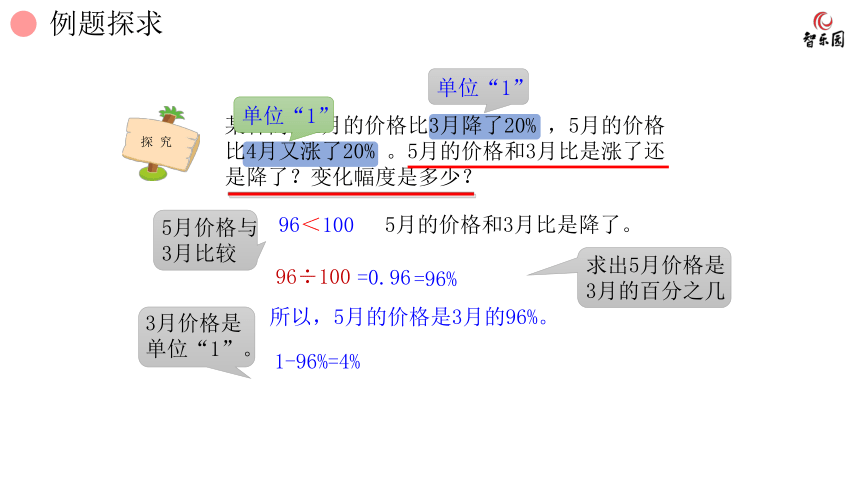
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
单位“1”
96
100
<
5月的价格和3月比是降了。
96÷100
=0.96
=96%
所以,5月的价格是3月的96%。
1-96%=4%
求出5月价格是
3月的百分之几
3月价格是
单位“1”。
探 究
例题探求
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
单位“1”
1×(1-20%)
(1+20%)
=0.96
(1-0.96)÷1
答: 5月的价格和3月比降了,降低了4%。
方法二:直接假设此商品3月价格是1。
×
=0.04
=4%
方法三:假设此商品3月价格是元。
×(1-20%)
(1+20%)
=0.96
( -0.96 )÷
×
=0.04
=4%
探 究
例题探求
因为单位“1”不同。
请想一想,为什么降价和涨价的幅度都是20%,但降价和涨价的具体钱数却不同呢?
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
单位“1”
例题探求
无论3月的价格具体取值是多少,结果都是一样的。
把3月的价格假设为 元
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
小小练习
某电视机厂计划某种型号的电视机比去年增产50%,实际又比
计划的产量多生产了10%。此型号的电视机今年的实际产量是
去年的百分之多少?
去年电视机的产量是单位“1”
计划的产量是单位“1”
今年计划的产量
去年的产量
×
今年占去年产量的百分比
=
今年实际的产量
计划的产量
×
实际占计划产量的百分比
=
今年实际的产量
÷
去年的产量
=
实际占去年产量的百分比
小小练习
答:今年的实际产量是去年的165%。
方法一:假设去年产量是100台。
(1)今年计划产量:100×(1+50%)=100×150%=150(台)
(2)今年实际产量:150×(1+10%)=150×110%=165(台)
(3)165÷100×100%=165%
某电视机厂计划某种型号的电视机比去年增产50%,实际又比
计划的产量多生产了10%。此型号的电视机今年的实际产量是
去年的百分之多少?
小小练习
答:今年的实际产量是去年的165%。
方法二:假设去年产量是1。
(1)今年计划产量:1×(1+50%)=1×150%=1.5
(2)今年实际产量:1.5×(1+10%)=1.5×110%=1.65
(3)1.65÷1×100%=165%
某电视机厂计划某种型号的电视机比去年增产50%,实际又比
计划的产量多生产了10%。此型号的电视机今年的实际产量是
去年的百分之多少?
小小练习
(一)基本练习
1 .一台笔记本先降价10%,再涨价10%,现价是原价的百分之几?
2.一台笔记本先涨价10%,再降价10%,现价是原价的百分之几?
你发现了什么?
1 ×(1-10%) ×(1+10%)=0.99
0.99 ÷1=0.99=99%
1 ×(1+10%) ×(1-10%)=0.99
0.99 ÷1=0.99=99%
如果涨价、降价的幅度一致,那么“先涨再降”和“先降再涨”的结果是一样的。
小小练习
(二)变式练习
1 .长方形的长增加25%,宽减少20%,面积变大还是变小了?
2.商店对某饮料推出了“第二杯半价”的促销办法,若卖出两杯这种饮料,相当于按原价的百分之几销售?
假设长方形的长是 ,宽是 。
答:面积没有变。
假设饮料价格为 ,则第二杯价格为 。
答:相当于按原价的75%销售。
小小练习
(三)提高练习
一根绳子,第一次剪去20%,第二次剪去余下的20%,第三次剪去余下的20%,还剩全长的百分之几?
假设绳子长为 。
第一次剪去:
第二次剪去:
第三次剪去:
剩余长度:
答:还剩全长的51.2%。
归纳小结
假设法
单位“1”不论假设为多少,最后的结果都不受影响。
可以用假设法解决有关百分数连续变化的问题,相对来说把单位“1”假设为“1”比较简单和方便。
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
解决问题
人教版 六年级上册
情境导入
(一)只列式不计算:
1.180米增加20%是多少米?
2 .图书馆有故事类书籍2000册,历史类书籍1500册,历史类书籍比故事类书籍少百分之几?
180×(1+20%)
(2000-1500)÷2000
情境导入
(二)找出下列题目中表示单位“1”的量:
1 .连环画的本数是故事数本数的37.5%;
2 .果园里苹果树的棵树比梨树多50%;
3 .冰箱售价1800元,十一商场搞活动,降了10%。
例题探求
4月价格=
方法一:假设此商
品3月价格是100元。
3月价格
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
×
(1-20%)
单位“1”
4月价格
×
(1+20%)
4月价格:
100
×
(1-20%)
=100×0.8
=80(元)
5月价格:
80
×
(1+20%)
=80×1.2
=96(元)
5月价格=
探 究
例题探求
5月价格与
3月比较
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
单位“1”
96
100
<
5月的价格和3月比是降了。
96÷100
=0.96
=96%
所以,5月的价格是3月的96%。
1-96%=4%
求出5月价格是
3月的百分之几
3月价格是
单位“1”。
探 究
例题探求
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
单位“1”
1×(1-20%)
(1+20%)
=0.96
(1-0.96)÷1
答: 5月的价格和3月比降了,降低了4%。
方法二:直接假设此商品3月价格是1。
×
=0.04
=4%
方法三:假设此商品3月价格是元。
×(1-20%)
(1+20%)
=0.96
( -0.96 )÷
×
=0.04
=4%
探 究
例题探求
因为单位“1”不同。
请想一想,为什么降价和涨价的幅度都是20%,但降价和涨价的具体钱数却不同呢?
某种商品4月的价格比3月降了20% ,5月的价格比4月又涨了20% 。5月的价格和3月比是涨了还是降了?变化幅度是多少?
单位“1”
单位“1”
例题探求
无论3月的价格具体取值是多少,结果都是一样的。
把3月的价格假设为 元
某种商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。5月的价格和3月比是涨了还是降了?变化幅度是多少?
小小练习
某电视机厂计划某种型号的电视机比去年增产50%,实际又比
计划的产量多生产了10%。此型号的电视机今年的实际产量是
去年的百分之多少?
去年电视机的产量是单位“1”
计划的产量是单位“1”
今年计划的产量
去年的产量
×
今年占去年产量的百分比
=
今年实际的产量
计划的产量
×
实际占计划产量的百分比
=
今年实际的产量
÷
去年的产量
=
实际占去年产量的百分比
小小练习
答:今年的实际产量是去年的165%。
方法一:假设去年产量是100台。
(1)今年计划产量:100×(1+50%)=100×150%=150(台)
(2)今年实际产量:150×(1+10%)=150×110%=165(台)
(3)165÷100×100%=165%
某电视机厂计划某种型号的电视机比去年增产50%,实际又比
计划的产量多生产了10%。此型号的电视机今年的实际产量是
去年的百分之多少?
小小练习
答:今年的实际产量是去年的165%。
方法二:假设去年产量是1。
(1)今年计划产量:1×(1+50%)=1×150%=1.5
(2)今年实际产量:1.5×(1+10%)=1.5×110%=1.65
(3)1.65÷1×100%=165%
某电视机厂计划某种型号的电视机比去年增产50%,实际又比
计划的产量多生产了10%。此型号的电视机今年的实际产量是
去年的百分之多少?
小小练习
(一)基本练习
1 .一台笔记本先降价10%,再涨价10%,现价是原价的百分之几?
2.一台笔记本先涨价10%,再降价10%,现价是原价的百分之几?
你发现了什么?
1 ×(1-10%) ×(1+10%)=0.99
0.99 ÷1=0.99=99%
1 ×(1+10%) ×(1-10%)=0.99
0.99 ÷1=0.99=99%
如果涨价、降价的幅度一致,那么“先涨再降”和“先降再涨”的结果是一样的。
小小练习
(二)变式练习
1 .长方形的长增加25%,宽减少20%,面积变大还是变小了?
2.商店对某饮料推出了“第二杯半价”的促销办法,若卖出两杯这种饮料,相当于按原价的百分之几销售?
假设长方形的长是 ,宽是 。
答:面积没有变。
假设饮料价格为 ,则第二杯价格为 。
答:相当于按原价的75%销售。
小小练习
(三)提高练习
一根绳子,第一次剪去20%,第二次剪去余下的20%,第三次剪去余下的20%,还剩全长的百分之几?
假设绳子长为 。
第一次剪去:
第二次剪去:
第三次剪去:
剩余长度:
答:还剩全长的51.2%。
归纳小结
假设法
单位“1”不论假设为多少,最后的结果都不受影响。
可以用假设法解决有关百分数连续变化的问题,相对来说把单位“1”假设为“1”比较简单和方便。
声明
本文件仅用于非商业性或非盈利性用途,使用时应遵守各项法律规定,不得侵犯本公司及相关权利人的合法权利。将本文件任何内容用于其他用途时,需获得授权,如发现未经授权用于商业或盈利用途将追究侵权者的法律责任。
