2023-2024学年苏科版八年级数学上《第2章轴对称图形》章末强化提优训练(含答案)
文档属性
| 名称 | 2023-2024学年苏科版八年级数学上《第2章轴对称图形》章末强化提优训练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 12:38:15 | ||
图片预览




文档简介
2023-2024学年苏科版八年级数学上《第2章轴对称图形》章末强化提优训练
(时间:90分钟 满分:120分)
一.选择题(30分)
1.以下京剧脸谱中,不是轴对称图形的是( )
第1题图 第2题图 2.如图,△ABC与△A′B′C′关于直线l对称,∠A=50°,∠C=30°,则∠B′的度数为( )
A.90° B.100° C.70° D.80°
3.三角形纸片上有一点P,量得PA=3cm,PB=3cm,则点P一定( )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
4.如图,OC是∠AOB的平分线,PD⊥OA于点D,PD=2,则P点到OB的距离是( )
A.1 B.2 C.3 D.4
第3题图 第4题图 第5题图 第6题图
5.如图,AB∥CD,∠A=70°,AC=BC,则∠BCD的度数为( )
A.100° B.105° C.110° D.140°
6.如图,△ABC是等边三角形,则∠1+∠2的度数为( )
A.60° B.90° C.120° D.180°
7.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
第7题图 第8题图 第9题图 第10题图
8. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个.
A. 3个 B. 4个 C. 5个 D. 6个
9. 如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠BDE=2∠BCE;其中正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
10. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( )
A. 3 B. 4 C. 6 D. 5
二.填空题(30分)
11.如图小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是_______.
第11题图 第12题图 第13题图 第14题图
12.如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=20,则△PMN的周长为 .
13.如图,在第1个△A1BC中,∠B=20°,A1B=CB,在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E……按此做法继续下去,则第5个三角形中以A5为顶点的内角度数是___°
14.如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为____.
15.在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为____________.
16. 如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为________.
第16题图 第17题图 第18题图 第20题图
17.如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM周长的最小值为________cm.
18.如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,D是△ABC外一点,且△ADC≌△BOC,连接OD. 当α=_________时,△AOD是等腰三角形.
19. 在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若三角形ABC的边长为1,AE=2,则CD的长为________.
20.如图,△ABC中,BC的垂直平分线DP与∠BAC的平分线相交于点D,垂足为点P,连接BD,CD,若∠BAC=84°,则∠BDC=________.
三。解答题(60分)
21、(8分)用三角板和直尺作图.(不写作法,保留痕迹)
如图,点A,B在直线l的同侧.
(1)试在直线l上取一点M,使MA+MB的值最小.
(2)试在直线l上取一点N,使NB﹣NA最大.
22. (8分)已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
23. (8分)如图,一个四边形纸片ABCD,,把纸片按如图所示折叠,使点B落在AD边上的点,AE是折痕.
(1)判断与DC的位置关系,并说明理由;
(2)如果,求的度数.
24.(12分)已知Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB, CE所在的直线交AD于点F.
(1)如图1,若点D在△ABC外,点B在AB边上,
求证:AD=CE,AD⊥CE.
(2)若将图1中的△DBE绕点B顺时针旋转,使点E在△ABC内部,如图2,求证:AD=CE,AD⊥CE.
(3)若将图1中的△DBE绕点B逆时针旋转,使点D、E都在△ABC外部,如图3,请直出AD和CE的数量和位置关系.
25、(12分)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
.
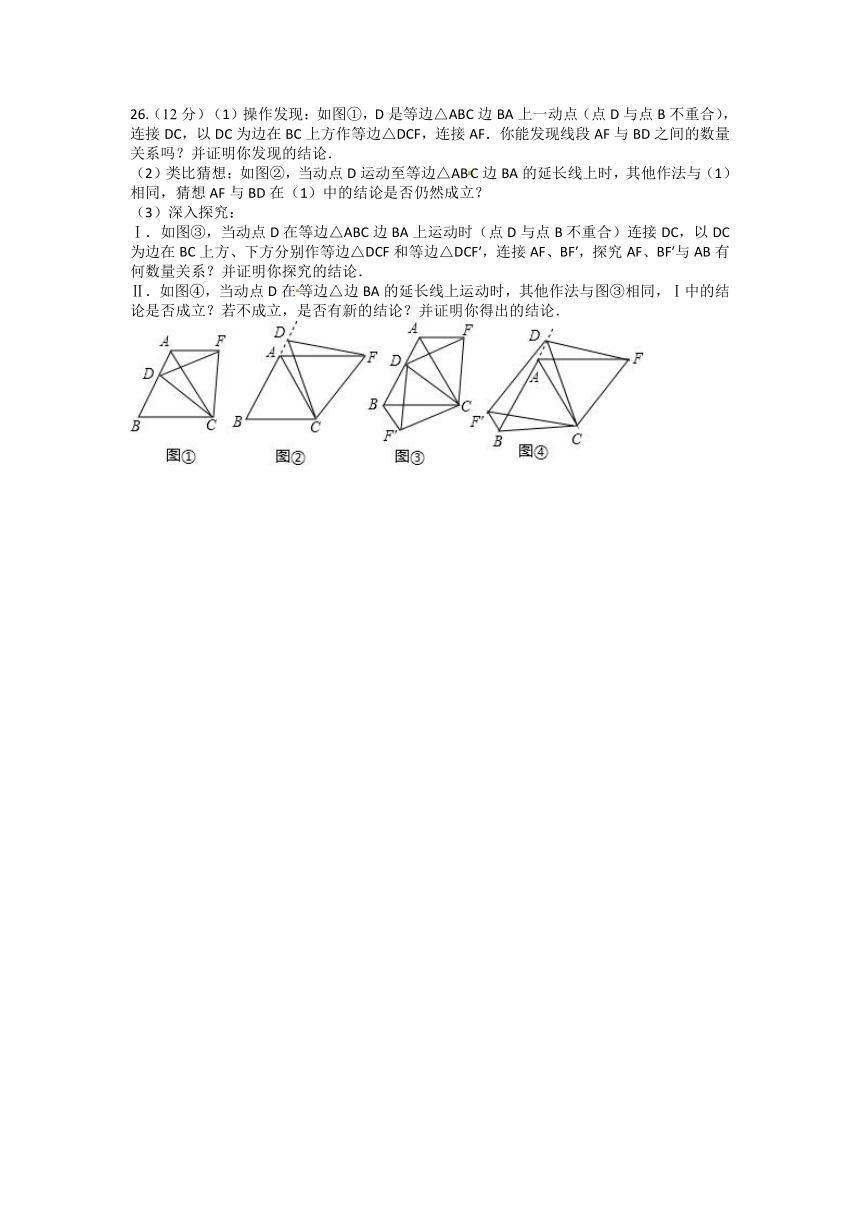
26.(12分)(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
教师样卷
一.选择题(30分)
1.以下京剧脸谱中,不是轴对称图形的是( C )
第1题图 第2题图 2.如图,△ABC与△A′B′C′关于直线l对称,∠A=50°,∠C=30°,则∠B′的度数为( B )
A.90° B.100° C.70° D.80°
3.三角形纸片上有一点P,量得PA=3cm,PB=3cm,则点P一定( D )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
4.如图,OC是∠AOB的平分线,PD⊥OA于点D,PD=2,则P点到OB的距离是( B )
A.1 B.2 C.3 D.4
第3题图 第4题图 第5题图 第6题图
5.如图,AB∥CD,∠A=70°,AC=BC,则∠BCD的度数为( C )
A.100° B.105° C.110° D.140°
6.如图,△ABC是等边三角形,则∠1+∠2的度数为( C )
A.60° B.90° C.120° D.180°
7.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( B )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
[解析] ∵在△ABC中,∠ACB=90°,DE⊥AB,∴∠ADE=∠ACB=90°.∴∠A+∠B=90°,∠ACD+∠DCB=90°.∵∠DCA=∠DAC,∴AD=CD,∠DCB=∠B.∴CD=BD.∴AD=BD,
∴CD=AB.故①②正确;∵∠DCA=∠DAC,∴AD=CD,但不能判定△ADC是等边三角形.故③错误;∵若∠E=30°,则∠A=60°,∠B=30°.∴△ACD是等边三角形.∴∠ADC=60°.
∵∠ADE=∠ACB=90°,∴∠EDC=∠BCD=∠B=30°.∴CF=DF,∴DE=EF+DF=EF+CF.
故④正确.故选B.
第7题图 第8题图 第9题图 第10题图
8. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( C )个.
A. 3个 B. 4个 C. 5个 D. 6个
解:如图所示:与△ABC成轴对称且以格点为顶点三角形有△ABG、△CDF、△AEF、△DBH,△BCG共5个,故选C.
9. 如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠BDE=2∠BCE;其中正确结论的个数为( D )
A. 0 B. 1 C. 2 D. 3
解: ∵∠BAC=60°,∴∠ABC+∠ACB=180°-60°=120°,∵BE、CE分别为∠ABC、∠ACB的平分线,∴∠EBC= ∠ABC,∠ECB=∠ACB,∴∠EBC+∠ECB=(∠ABC+∠ACB)=×120°=60°,∴∠BEC=180°-(∠EBC+∠ECB)=180°-60°=120°,故①正确;如图,过点D作DF⊥AB于F,DG⊥AC的延长线于G,∵BE、CE分别为∠ABC、∠ACB的平分线,
∴AD为∠BAC的平分线,∴DF=DG,∴∠FDG=360°-90°×2-60°=120°,又∵∠BDC=120°,
∴∠BDF+∠CDF=120°,∠CDG+∠CDF=120°,∴∠BDF=∠CDG,∵在△BDF和△CDG中,
∴△BDF≌△CDG(ASA),∴DB=CD,∴∠DBC=(180°-120°)=30°,∴∠DBE=∠DBC+∠CBE=30°+∠CBE,∵BE平分∠ABC,AE平分∠BAC,∴∠ABE=∠CBE,∠BAE=∠BAC=30°,根据三角形的外角性质,∠DEB=∠ABE+∠BAE=∠ABE+30°,∴∠DBE=∠DEB,∴DB=DE,故②正确;∵DB=DE=DC,∴B,C,E三点在以D为圆心,以BD为半径的圆上,∴∠BDE=2∠BCE,故③正确;综上所述,正确的结论有①②③共3个.
故选D.
10. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( D )
A. 3 B. 4 C. 6 D. 5
解: 作DF⊥AC于F,如图, ∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF=4,∵S△ADB+S△ADC=S△ABC,∴×4×7+×4×AC=24,∴AC=5,故选:D.
二.填空题(30分)
11.如图小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是__10:45______.
第11题图 第12题图 第13题图 第14题图
12.如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=20,则△PMN的周长为 20 .
13.如图,在第1个△A1BC中,∠B=20°,A1B=CB,在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E……按此做法继续下去,则第5个三角形中以A5为顶点的内角度数是__5__°
14.如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为__8__.
15.在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为___7或11_________.
16. 如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为___25°_____.
解: ∵△ABC沿EF翻折,∴∠BEF=∠B′EF,∠CFE=∠C′FE,∴180° ∠AEF=∠1+∠AEF,180° ∠AFE=∠2+∠AFE,∵∠1=95°,∴∠AEF=12(180° 95°)=42.5°,∵∠A+∠AEF+∠AFE=180°,∴∠AFE=180° 60° 42.5°=77.5°,∴180° 77.5=∠2+77.5°,∴∠2=25°.故答案为:25°.
第16题图 第17题图 第18题图 第20题图
17.如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM周长的最小值为___8_____cm.
解:如图,连接AD.∵△ABC是等腰三角形,点D是BC边的中点,∴BD=CD,AD⊥BC,∴S△ABC=BC·AD=×4·AD=12,解得AD=6cm.∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值.∴△BDM的周长最短为(BM+MD)+BD=AD+BC=6+×4=6+2=8(cm).故答案为8.
18.如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,D是△ABC外一点,且△ADC≌△BOC,连接OD. 当α=__125°,110°或140°_______时,△AOD是等腰三角形.
解: ① 要使AO=AD,需∠AOD=∠ADO.∵∠AOD=190°-α,∠ADO=α-60°,∴190°-α=α-60°,∴α=125°.② 要使OA=OD,需∠OAD=∠ADO.∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,∴α-60°-50°.∴α=110°.③要使AD=OD,需∠AOD=∠OAD,∴190°-α=50°.∴α=140°.综上所述,当α为125°,110°或140°时,△AOD是等腰三角形.
19. 在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若三角形ABC的边长为1,AE=2,则CD的长为___1或3_____.
解:当E在线段BA的延长线上,D在线段BC的延长线上时,如图1所示,过E作EF⊥BD,垂足为F点,可得∠EFB=90°,∵EC=ED,∴F为CD的中点,即CF=DF=CD,∵△ABC为等边三角形,∴∠ABC=60°,∴∠BEF=30°,∵BE=AB+AE=1+2=3,∴FB=EB=,∴CF=FB BC=,则CD=2CF=1;当E在线段AB的延长线上,D在线段CB的延长线上时,如图2所示,过E作EF⊥BD,垂足为F点,可得∠EFC=90°,∵EC=ED,
∴F为CD的中点,即CF=DF=CD,∵△ABC为等边三角形,∴∠ABC=∠EBF=60°,
∴∠BEF=30°,∵BE=AE AB=2 1=1,∴FB=BE=,∴CF=BC+FB=,则CD=2CF=3,
综上,CD的值为1或3.故答案为:1或3
20.如图,△ABC中,BC的垂直平分线DP与∠BAC的平分线相交于点D,垂足为点P,连接BD,CD,若∠BAC=84°,则∠BDC=___96°_____.
解:如图,过点D作DE⊥AB,交AB的延长线于点E,作DF⊥AC于点F.∵AD是∠BAC的平分线,∴DE=DF.∵DP是BC的垂直平分线,∴BD=CD.在Rt△DEB和Rt△DFC中,∴Rt△DEB≌Rt△DFC(HL),∴∠BDE=∠CDF,∴∠BDC=∠EDF.∵∠DEB=∠DFA=90°,∠BAC=84°,∴∠EDF=360°-90°-90°-84°=96°,∴∠BDC=96°.
三。解答题(60分)
21、(8分)用三角板和直尺作图.(不写作法,保留痕迹)
如图,点A,B在直线l的同侧.
(1)试在直线l上取一点M,使MA+MB的值最小.
(2)试在直线l上取一点N,使NB﹣NA最大.
解:(1)如图所示:(2)如图所示;
理由:∵NB﹣NA≤AB,∴当A、B、N共线时,BN﹣NA的值最大.
22. (8分)已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
解:(1)有4条,若∠ABC=10°,有8条.当∠ABC=20°,∵BD=DE=EF=FG=GM,
∴∠DEB=∠B,∠EDF=∠EFD,∠FEG=∠FGE,∠GFM=∠FMG∵∠EDF=2∠B=40°,∠FEG=3∠B=60°,∠AFG=4∠B=80°,∠AMG=5∠B=100°,∴同理:∠AMG将成为下一个等腰三角形的底角∵100°+100°>180°∴不会再由下一条折线∴共有四条拆线,分别是:DE、EF、FG,GM.同理:当∠ABC=10°,有8条符合条件的折线.
(2)由(1)可知∠EDF=2∠B=2m°,∠FEG=3∠B=3m°,∠AFG=4∠B=4m°,∵根据三角形内角和定理可知,需满足mn<90°,∴n<的整数.
23. (8分)如图,一个四边形纸片ABCD,,把纸片按如图所示折叠,使点B落在AD边上的点,AE是折痕.
(1)判断与DC的位置关系,并说明理由;
(2)如果,求的度数.
解:(1)由于是的折叠后形成的,,;
(2)折叠,△,,即,
,,.
24.(12分)已知Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB, CE所在的直线交AD于点F.
(1)如图1,若点D在△ABC外,点B在AB边上,
求证:AD=CE,AD⊥CE.
(2)若将图1中的△DBE绕点B顺时针旋转,使点E在△ABC内部,如图2,求证:AD=CE,AD⊥CE.
(3)若将图1中的△DBE绕点B逆时针旋转,使点D、E都在△ABC外部,如图3,请直出AD和CE的数量和位置关系.
解:(1)证明:在和中,,;,,,,,,,,;
(2)证明:,,即,
在和中,,,, ,,,,,,,;
(3),;理由如下:,,即,在和中,,,, ,,,,,,,.
25、(12分)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
.
解:问题探究:,理由如下:延长BE交CA延长线于F,∵CD平分,∴,在和中,,∴,∴.,∵,∴,∴,在和中,∴,∴,∴; 拓展延伸:.证明:过点D作,交BE的延长线于点G,与AE相交于H,∵,∴,,∵,∴.∵,∴,∴,∵,∴.
∵,,∴.∵,∴,∴,∴,在和中,,∴;∴,在和中,,∴∴, ∴.
27.(12分)(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
解:(1)AF=BD.证明如下:∵△ABC是等边三角形(已知),∴BC=AC,∠BCA=60°(等边三角形的性质).同理知,DC=CF,∠DCF=60°.∴∠BCA-∠DCA=∠DCF-∠DCA,即∠BCD=∠ACF.在△BCD和△ACF中,∴△BCD≌△ACF(SAS).∴BD=AF(全等三角形的对应边相等).
(2)证明过程同(1),证得△BCD≌△ACF(SAS),则AF=BD(全等三角形的对应边相等),所以当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,AF=BD仍然成立.
(3)Ⅰ.AF+BF′=AB.证明如下:由(1)知,△BCD≌△ACF(SAS),则BD=AF;同理△BCF′≌△ACD,则BF′=AD.∴AF+BF′=BD+AD=AB;Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′.证明如下:在△BCF′和△ACD中,∴△BCF′≌△ACD(SAS).∴BF′=AD(全等三角形的对应边相等).又由(2)知,AF=BD,∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.
(时间:90分钟 满分:120分)
一.选择题(30分)
1.以下京剧脸谱中,不是轴对称图形的是( )
第1题图 第2题图 2.如图,△ABC与△A′B′C′关于直线l对称,∠A=50°,∠C=30°,则∠B′的度数为( )
A.90° B.100° C.70° D.80°
3.三角形纸片上有一点P,量得PA=3cm,PB=3cm,则点P一定( )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
4.如图,OC是∠AOB的平分线,PD⊥OA于点D,PD=2,则P点到OB的距离是( )
A.1 B.2 C.3 D.4
第3题图 第4题图 第5题图 第6题图
5.如图,AB∥CD,∠A=70°,AC=BC,则∠BCD的度数为( )
A.100° B.105° C.110° D.140°
6.如图,△ABC是等边三角形,则∠1+∠2的度数为( )
A.60° B.90° C.120° D.180°
7.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
第7题图 第8题图 第9题图 第10题图
8. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个.
A. 3个 B. 4个 C. 5个 D. 6个
9. 如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠BDE=2∠BCE;其中正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
10. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( )
A. 3 B. 4 C. 6 D. 5
二.填空题(30分)
11.如图小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是_______.
第11题图 第12题图 第13题图 第14题图
12.如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=20,则△PMN的周长为 .
13.如图,在第1个△A1BC中,∠B=20°,A1B=CB,在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E……按此做法继续下去,则第5个三角形中以A5为顶点的内角度数是___°
14.如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为____.
15.在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为____________.
16. 如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为________.
第16题图 第17题图 第18题图 第20题图
17.如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM周长的最小值为________cm.
18.如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,D是△ABC外一点,且△ADC≌△BOC,连接OD. 当α=_________时,△AOD是等腰三角形.
19. 在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若三角形ABC的边长为1,AE=2,则CD的长为________.
20.如图,△ABC中,BC的垂直平分线DP与∠BAC的平分线相交于点D,垂足为点P,连接BD,CD,若∠BAC=84°,则∠BDC=________.
三。解答题(60分)
21、(8分)用三角板和直尺作图.(不写作法,保留痕迹)
如图,点A,B在直线l的同侧.
(1)试在直线l上取一点M,使MA+MB的值最小.
(2)试在直线l上取一点N,使NB﹣NA最大.
22. (8分)已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
23. (8分)如图,一个四边形纸片ABCD,,把纸片按如图所示折叠,使点B落在AD边上的点,AE是折痕.
(1)判断与DC的位置关系,并说明理由;
(2)如果,求的度数.
24.(12分)已知Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB, CE所在的直线交AD于点F.
(1)如图1,若点D在△ABC外,点B在AB边上,
求证:AD=CE,AD⊥CE.
(2)若将图1中的△DBE绕点B顺时针旋转,使点E在△ABC内部,如图2,求证:AD=CE,AD⊥CE.
(3)若将图1中的△DBE绕点B逆时针旋转,使点D、E都在△ABC外部,如图3,请直出AD和CE的数量和位置关系.
25、(12分)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
.
26.(12分)(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
教师样卷
一.选择题(30分)
1.以下京剧脸谱中,不是轴对称图形的是( C )
第1题图 第2题图 2.如图,△ABC与△A′B′C′关于直线l对称,∠A=50°,∠C=30°,则∠B′的度数为( B )
A.90° B.100° C.70° D.80°
3.三角形纸片上有一点P,量得PA=3cm,PB=3cm,则点P一定( D )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
4.如图,OC是∠AOB的平分线,PD⊥OA于点D,PD=2,则P点到OB的距离是( B )
A.1 B.2 C.3 D.4
第3题图 第4题图 第5题图 第6题图
5.如图,AB∥CD,∠A=70°,AC=BC,则∠BCD的度数为( C )
A.100° B.105° C.110° D.140°
6.如图,△ABC是等边三角形,则∠1+∠2的度数为( C )
A.60° B.90° C.120° D.180°
7.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( B )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
[解析] ∵在△ABC中,∠ACB=90°,DE⊥AB,∴∠ADE=∠ACB=90°.∴∠A+∠B=90°,∠ACD+∠DCB=90°.∵∠DCA=∠DAC,∴AD=CD,∠DCB=∠B.∴CD=BD.∴AD=BD,
∴CD=AB.故①②正确;∵∠DCA=∠DAC,∴AD=CD,但不能判定△ADC是等边三角形.故③错误;∵若∠E=30°,则∠A=60°,∠B=30°.∴△ACD是等边三角形.∴∠ADC=60°.
∵∠ADE=∠ACB=90°,∴∠EDC=∠BCD=∠B=30°.∴CF=DF,∴DE=EF+DF=EF+CF.
故④正确.故选B.
第7题图 第8题图 第9题图 第10题图
8. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( C )个.
A. 3个 B. 4个 C. 5个 D. 6个
解:如图所示:与△ABC成轴对称且以格点为顶点三角形有△ABG、△CDF、△AEF、△DBH,△BCG共5个,故选C.
9. 如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠BDE=2∠BCE;其中正确结论的个数为( D )
A. 0 B. 1 C. 2 D. 3
解: ∵∠BAC=60°,∴∠ABC+∠ACB=180°-60°=120°,∵BE、CE分别为∠ABC、∠ACB的平分线,∴∠EBC= ∠ABC,∠ECB=∠ACB,∴∠EBC+∠ECB=(∠ABC+∠ACB)=×120°=60°,∴∠BEC=180°-(∠EBC+∠ECB)=180°-60°=120°,故①正确;如图,过点D作DF⊥AB于F,DG⊥AC的延长线于G,∵BE、CE分别为∠ABC、∠ACB的平分线,
∴AD为∠BAC的平分线,∴DF=DG,∴∠FDG=360°-90°×2-60°=120°,又∵∠BDC=120°,
∴∠BDF+∠CDF=120°,∠CDG+∠CDF=120°,∴∠BDF=∠CDG,∵在△BDF和△CDG中,
∴△BDF≌△CDG(ASA),∴DB=CD,∴∠DBC=(180°-120°)=30°,∴∠DBE=∠DBC+∠CBE=30°+∠CBE,∵BE平分∠ABC,AE平分∠BAC,∴∠ABE=∠CBE,∠BAE=∠BAC=30°,根据三角形的外角性质,∠DEB=∠ABE+∠BAE=∠ABE+30°,∴∠DBE=∠DEB,∴DB=DE,故②正确;∵DB=DE=DC,∴B,C,E三点在以D为圆心,以BD为半径的圆上,∴∠BDE=2∠BCE,故③正确;综上所述,正确的结论有①②③共3个.
故选D.
10. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( D )
A. 3 B. 4 C. 6 D. 5
解: 作DF⊥AC于F,如图, ∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF=4,∵S△ADB+S△ADC=S△ABC,∴×4×7+×4×AC=24,∴AC=5,故选:D.
二.填空题(30分)
11.如图小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是__10:45______.
第11题图 第12题图 第13题图 第14题图
12.如图,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=20,则△PMN的周长为 20 .
13.如图,在第1个△A1BC中,∠B=20°,A1B=CB,在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E……按此做法继续下去,则第5个三角形中以A5为顶点的内角度数是__5__°
14.如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为__8__.
15.在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为___7或11_________.
16. 如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为___25°_____.
解: ∵△ABC沿EF翻折,∴∠BEF=∠B′EF,∠CFE=∠C′FE,∴180° ∠AEF=∠1+∠AEF,180° ∠AFE=∠2+∠AFE,∵∠1=95°,∴∠AEF=12(180° 95°)=42.5°,∵∠A+∠AEF+∠AFE=180°,∴∠AFE=180° 60° 42.5°=77.5°,∴180° 77.5=∠2+77.5°,∴∠2=25°.故答案为:25°.
第16题图 第17题图 第18题图 第20题图
17.如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM周长的最小值为___8_____cm.
解:如图,连接AD.∵△ABC是等腰三角形,点D是BC边的中点,∴BD=CD,AD⊥BC,∴S△ABC=BC·AD=×4·AD=12,解得AD=6cm.∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值.∴△BDM的周长最短为(BM+MD)+BD=AD+BC=6+×4=6+2=8(cm).故答案为8.
18.如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,D是△ABC外一点,且△ADC≌△BOC,连接OD. 当α=__125°,110°或140°_______时,△AOD是等腰三角形.
解: ① 要使AO=AD,需∠AOD=∠ADO.∵∠AOD=190°-α,∠ADO=α-60°,∴190°-α=α-60°,∴α=125°.② 要使OA=OD,需∠OAD=∠ADO.∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,∴α-60°-50°.∴α=110°.③要使AD=OD,需∠AOD=∠OAD,∴190°-α=50°.∴α=140°.综上所述,当α为125°,110°或140°时,△AOD是等腰三角形.
19. 在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若三角形ABC的边长为1,AE=2,则CD的长为___1或3_____.
解:当E在线段BA的延长线上,D在线段BC的延长线上时,如图1所示,过E作EF⊥BD,垂足为F点,可得∠EFB=90°,∵EC=ED,∴F为CD的中点,即CF=DF=CD,∵△ABC为等边三角形,∴∠ABC=60°,∴∠BEF=30°,∵BE=AB+AE=1+2=3,∴FB=EB=,∴CF=FB BC=,则CD=2CF=1;当E在线段AB的延长线上,D在线段CB的延长线上时,如图2所示,过E作EF⊥BD,垂足为F点,可得∠EFC=90°,∵EC=ED,
∴F为CD的中点,即CF=DF=CD,∵△ABC为等边三角形,∴∠ABC=∠EBF=60°,
∴∠BEF=30°,∵BE=AE AB=2 1=1,∴FB=BE=,∴CF=BC+FB=,则CD=2CF=3,
综上,CD的值为1或3.故答案为:1或3
20.如图,△ABC中,BC的垂直平分线DP与∠BAC的平分线相交于点D,垂足为点P,连接BD,CD,若∠BAC=84°,则∠BDC=___96°_____.
解:如图,过点D作DE⊥AB,交AB的延长线于点E,作DF⊥AC于点F.∵AD是∠BAC的平分线,∴DE=DF.∵DP是BC的垂直平分线,∴BD=CD.在Rt△DEB和Rt△DFC中,∴Rt△DEB≌Rt△DFC(HL),∴∠BDE=∠CDF,∴∠BDC=∠EDF.∵∠DEB=∠DFA=90°,∠BAC=84°,∴∠EDF=360°-90°-90°-84°=96°,∴∠BDC=96°.
三。解答题(60分)
21、(8分)用三角板和直尺作图.(不写作法,保留痕迹)
如图,点A,B在直线l的同侧.
(1)试在直线l上取一点M,使MA+MB的值最小.
(2)试在直线l上取一点N,使NB﹣NA最大.
解:(1)如图所示:(2)如图所示;
理由:∵NB﹣NA≤AB,∴当A、B、N共线时,BN﹣NA的值最大.
22. (8分)已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
解:(1)有4条,若∠ABC=10°,有8条.当∠ABC=20°,∵BD=DE=EF=FG=GM,
∴∠DEB=∠B,∠EDF=∠EFD,∠FEG=∠FGE,∠GFM=∠FMG∵∠EDF=2∠B=40°,∠FEG=3∠B=60°,∠AFG=4∠B=80°,∠AMG=5∠B=100°,∴同理:∠AMG将成为下一个等腰三角形的底角∵100°+100°>180°∴不会再由下一条折线∴共有四条拆线,分别是:DE、EF、FG,GM.同理:当∠ABC=10°,有8条符合条件的折线.
(2)由(1)可知∠EDF=2∠B=2m°,∠FEG=3∠B=3m°,∠AFG=4∠B=4m°,∵根据三角形内角和定理可知,需满足mn<90°,∴n<的整数.
23. (8分)如图,一个四边形纸片ABCD,,把纸片按如图所示折叠,使点B落在AD边上的点,AE是折痕.
(1)判断与DC的位置关系,并说明理由;
(2)如果,求的度数.
解:(1)由于是的折叠后形成的,,;
(2)折叠,△,,即,
,,.
24.(12分)已知Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB, CE所在的直线交AD于点F.
(1)如图1,若点D在△ABC外,点B在AB边上,
求证:AD=CE,AD⊥CE.
(2)若将图1中的△DBE绕点B顺时针旋转,使点E在△ABC内部,如图2,求证:AD=CE,AD⊥CE.
(3)若将图1中的△DBE绕点B逆时针旋转,使点D、E都在△ABC外部,如图3,请直出AD和CE的数量和位置关系.
解:(1)证明:在和中,,;,,,,,,,,;
(2)证明:,,即,
在和中,,,, ,,,,,,,;
(3),;理由如下:,,即,在和中,,,, ,,,,,,,.
25、(12分)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分.点A为OM上一点,过点A作,垂足为C,延长AC交ON于点B,可根据ASA证明,则,(即点C为AB的中点).
【问题探究】如图2,中,,,CD平分,,垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
【拓展延伸】如图3,中,,,点D在线段BC上,且, 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
.
解:问题探究:,理由如下:延长BE交CA延长线于F,∵CD平分,∴,在和中,,∴,∴.,∵,∴,∴,在和中,∴,∴,∴; 拓展延伸:.证明:过点D作,交BE的延长线于点G,与AE相交于H,∵,∴,,∵,∴.∵,∴,∴,∵,∴.
∵,,∴.∵,∴,∴,∴,在和中,,∴;∴,在和中,,∴∴, ∴.
27.(12分)(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
解:(1)AF=BD.证明如下:∵△ABC是等边三角形(已知),∴BC=AC,∠BCA=60°(等边三角形的性质).同理知,DC=CF,∠DCF=60°.∴∠BCA-∠DCA=∠DCF-∠DCA,即∠BCD=∠ACF.在△BCD和△ACF中,∴△BCD≌△ACF(SAS).∴BD=AF(全等三角形的对应边相等).
(2)证明过程同(1),证得△BCD≌△ACF(SAS),则AF=BD(全等三角形的对应边相等),所以当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,AF=BD仍然成立.
(3)Ⅰ.AF+BF′=AB.证明如下:由(1)知,△BCD≌△ACF(SAS),则BD=AF;同理△BCF′≌△ACD,则BF′=AD.∴AF+BF′=BD+AD=AB;Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′.证明如下:在△BCF′和△ACD中,∴△BCF′≌△ACD(SAS).∴BF′=AD(全等三角形的对应边相等).又由(2)知,AF=BD,∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
