18.1变量与函数课件(1)(广西壮族自治区防城港市防城区)
文档属性
| 名称 | 18.1变量与函数课件(1)(广西壮族自治区防城港市防城区) |

|
|
| 格式 | rar | ||
| 文件大小 | 638.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-09 00:00:00 | ||
图片预览







文档简介
课件20张PPT。§18.1 变量与函数 (1)第18章 函数及其图象那梭中学初二级数学备课组授课人:
教学目的:(1)让学生了解实践问题中数量之 间的依存关系,引出函数关系;(2)掌握函数定义的几个基本要素: 函数关系式,函数自变量的取值范围
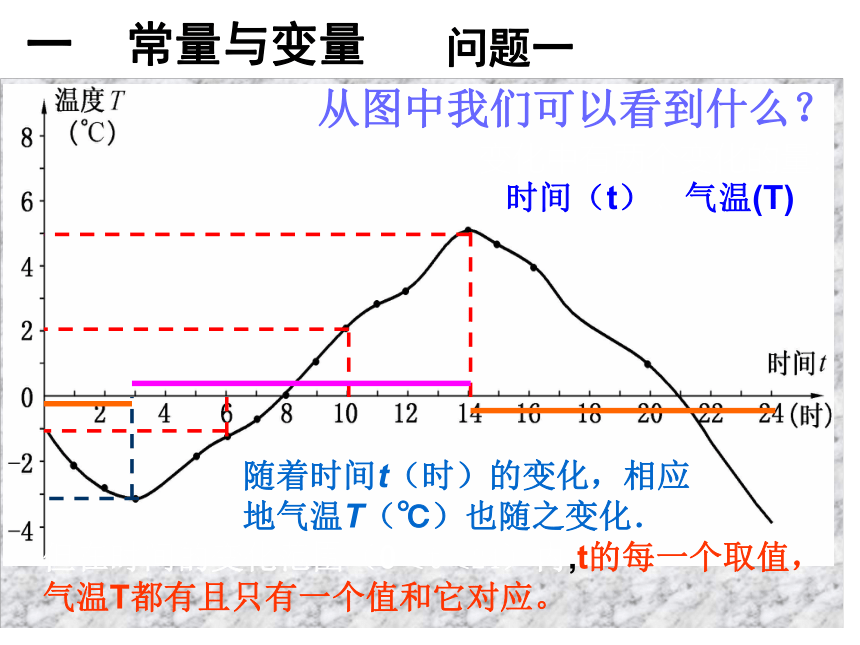
和函数概念,函数的表达方式。 大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢? 数学上常用变量与函数来刻画各种运动变化。 这一章我们将通过实际问题着重研究有关函数及其图像的初步知识。问题一一 常量与变量从图中我们可以看到什么?随着时间t(时)的变化,相应地气温T(℃)也随之变化.变化中有两个变化的量:时间(t)、气温(T)但在时间的变化范围(0≤t≤24)内,t的每一个取值,气温T都有且只有一个值和它对应。
?如图某地一天内的气温变化图。(看课本)看图回答:(1)这天的6时、10时和14时的气温分别是多少?(2)这一天中,最高气温是多少?最低气温是多少?
(3)在这一天中,什么时候气温在逐渐升高?什么时候气温在逐渐降低?解: (1)这天的6时、10时和14时的气温分别为-1℃、2℃、5℃ (2)这一天中,最高气温是5℃.最低气温是-4℃; (3)这一天中,3时~14时的气温在逐渐升高.
0时~3时和14时~24时的气温在逐渐降低. 问题1从上图中我们可以看到,随着时间t(时)的变化,
相应地气温T(℃)也随之变化.那么在生活中是否还有
其它类似的数量关系呢? 我们来观察下面的数据问题2 银行对各种不同的存款方式都规定了相应的利率,
下表是2002年7月中国工商银行为“整存整取”的存款
方式规定的年利率。观察上表,说一说随着x的增长,
相应的年利率y是怎样变化的。解: 随着存期x的增长,相应的年利率
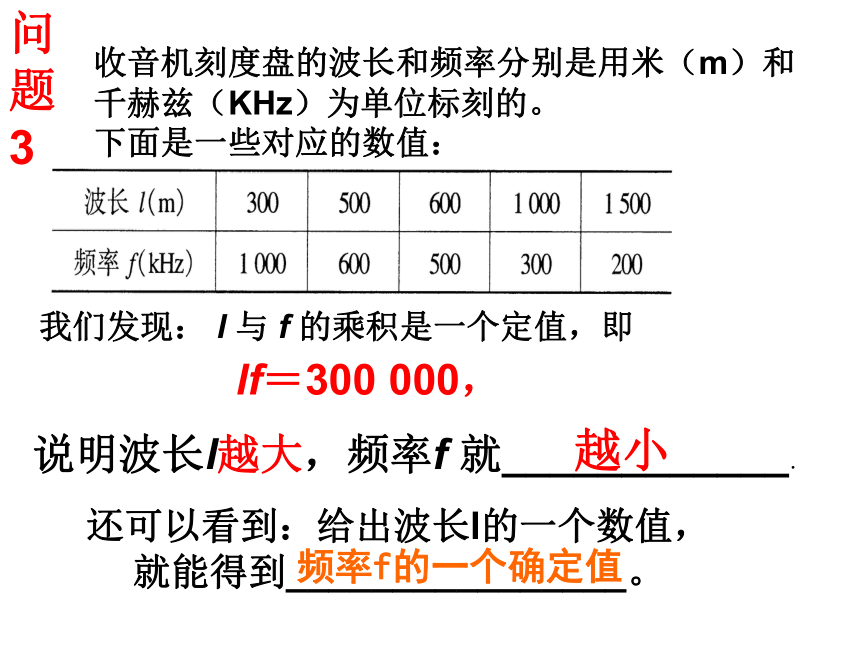
y也随着增长 问题3 收音机刻度盘的波长和频率分别是用米(m)和
千赫兹(KHz)为单位标刻的。
下面是一些对应的数值:我们发现: l 与 f 的乘积是一个定值,即 lf=300 000, 说明波长l越大,频率f 就____________.越小还可以看到:给出波长l的一个数值,
就能得到________________。频率f的一个确定值圆的面积随着半径的增大而增大.如果用r
表示圆的半径,S表示圆的面积则S与r之间
满足下列关系:S=_________.
利用这个关系式,试求出半径为1 cm、
1.5 cm、2 cm、2.6 cm、3.2 cm时圆的面积,
并将结果填入下表:由此可以看出,圆的半径越大,
它的面积就_________.πr2大问题4在上面的问题中,我们研究了一些数量间的
变化规律,他们都刻画了某些变化规律。这
里出现的量有一些它的数值会变化.例如问提1
中时间t和气温T,气温T随时间t的变化而变化,
问题2中年利率y随存期x的变化而变化,问题3
中频率f随波长l的变化而变化,问题4中圆的
面积s随半径r的变化而变化.
像这样在某一变化过程中,可以取
不同数值的量叫变量一般地,在一个变化过程中有两个量,
例如x和y。如果对于x的每一个值y都有
唯一值与之对应,就说x是自变量, y是因变量,有时也称y是x的函数.
自变量:是指在他的取值范围内可以随心所欲的,
自由自在的取它想取的值,看这概念够贴切了吧。
因变量:这个“因”字是指因x的变化,通过一定的
关系而得到的。 在问题①中,t 是自变量,T是因变量。
在问题②中,x是自变量,y是因变量。
在问题③中,l是自变量,f是因变量。
在问题④中,r是自变量, S是因变量。
“y有唯一值与之对应”是指在自变量的取值范围内,x每取一个确定的值,y都有唯一的值与之对应,否则y不是x的函数;例 下列关系中,y不是x的函数的有:不是每一种函数关系都可以用代数式表示
出来的,通常表示函数关系的方法有三种:
1、图像法,如问题1;
2、列表法,如问题2和问题3中的列表;
3、解析法,即列出函数关系的解析式,
如问题3和问题4 。
当然对于同一个函数也可以选择不同的
函数表达关系式。在有些问题中,还有一些量它的数值始终都保持不变,
这样的量称为常量.如问题3中300000,
问题4中的π 练 习(1)从表中你能看出该市14岁的男学生的平均身高是多少吗?
(2)该市男学生的平均身高从哪一岁开始迅速增加?
(3)上表反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?2.解:2.下表是某市2000年统计的该市男学生各年龄组的平均身高.1.举3个日常生活中遇到的函数关系的例子.(1) 14岁的男学生的平均身高是146.1cm. (2)约从11岁开始身高迅速增加.(3) 反映了该市男学生的平均身高和年龄这两个变量之间的关系,其中年龄是自变量,平均身高是因变量.3.写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)火车以90千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.3.解:(2) s=90t, S=(n-2) ×180, (1)C=2?r, 2、 ?是常量,r和C是变量. 90是常量,t和s是变量.2和180是常量, n和S是变量.(1).一辆汽车以40千米/小时的速度行驶,写出行驶路程s(千米)与行驶时间t(时)的关系式。 解:S=40t 其中t是自变量,S是因变量
40是常量(2).一辆汽车行驶5小时,写出行驶路程s
(千米)与行驶速度v(千米/小时)之间的关系式 解:S=5V 其中V是自变量,S是因变量
5是常量练习二写出下列各问题中的关系式,并指出其中
的自变量,因变量和常量(3)三角形的其中两边分别为2,4,
则三角形第三边x与三角形的周长y之间的关系 解: y =6+ x ,其中x是自变量,
y是因变量6是常量练习三某电信公司手机的A类收费标准如下:不管通话时间
多长、每部手机必须缴月租50元外,每通话1分交费0.4元。(1)写出每月应缴费用y(元)和通话时间x(分)之间的关系式; ?(2)某手机用户这个月通话时间为152分,他应缴费多少元?(3)如果一手机用户本月交了200元的费用,他通话的时间是多少分钟? 解:(1)y=50+0.4x(2)当x=152时,y=50+152×0.4=110.8(元)(3)当y=200时,200=50+0.4x,
解这个方程得x=375(分)答:略小结:一 常量与变量 在某一变化过程中,可以取不同数值的量,叫做变量. 在研究问题的过程中,取值始终保持不变的量,叫做常量.二 函数函数的定义: 如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数. 作业习题18.1的 1.
教学目的:(1)让学生了解实践问题中数量之 间的依存关系,引出函数关系;(2)掌握函数定义的几个基本要素: 函数关系式,函数自变量的取值范围
和函数概念,函数的表达方式。 大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢? 数学上常用变量与函数来刻画各种运动变化。 这一章我们将通过实际问题着重研究有关函数及其图像的初步知识。问题一一 常量与变量从图中我们可以看到什么?随着时间t(时)的变化,相应地气温T(℃)也随之变化.变化中有两个变化的量:时间(t)、气温(T)但在时间的变化范围(0≤t≤24)内,t的每一个取值,气温T都有且只有一个值和它对应。
?如图某地一天内的气温变化图。(看课本)看图回答:(1)这天的6时、10时和14时的气温分别是多少?(2)这一天中,最高气温是多少?最低气温是多少?
(3)在这一天中,什么时候气温在逐渐升高?什么时候气温在逐渐降低?解: (1)这天的6时、10时和14时的气温分别为-1℃、2℃、5℃ (2)这一天中,最高气温是5℃.最低气温是-4℃; (3)这一天中,3时~14时的气温在逐渐升高.
0时~3时和14时~24时的气温在逐渐降低. 问题1从上图中我们可以看到,随着时间t(时)的变化,
相应地气温T(℃)也随之变化.那么在生活中是否还有
其它类似的数量关系呢? 我们来观察下面的数据问题2 银行对各种不同的存款方式都规定了相应的利率,
下表是2002年7月中国工商银行为“整存整取”的存款
方式规定的年利率。观察上表,说一说随着x的增长,
相应的年利率y是怎样变化的。解: 随着存期x的增长,相应的年利率
y也随着增长 问题3 收音机刻度盘的波长和频率分别是用米(m)和
千赫兹(KHz)为单位标刻的。
下面是一些对应的数值:我们发现: l 与 f 的乘积是一个定值,即 lf=300 000, 说明波长l越大,频率f 就____________.越小还可以看到:给出波长l的一个数值,
就能得到________________。频率f的一个确定值圆的面积随着半径的增大而增大.如果用r
表示圆的半径,S表示圆的面积则S与r之间
满足下列关系:S=_________.
利用这个关系式,试求出半径为1 cm、
1.5 cm、2 cm、2.6 cm、3.2 cm时圆的面积,
并将结果填入下表:由此可以看出,圆的半径越大,
它的面积就_________.πr2大问题4在上面的问题中,我们研究了一些数量间的
变化规律,他们都刻画了某些变化规律。这
里出现的量有一些它的数值会变化.例如问提1
中时间t和气温T,气温T随时间t的变化而变化,
问题2中年利率y随存期x的变化而变化,问题3
中频率f随波长l的变化而变化,问题4中圆的
面积s随半径r的变化而变化.
像这样在某一变化过程中,可以取
不同数值的量叫变量一般地,在一个变化过程中有两个量,
例如x和y。如果对于x的每一个值y都有
唯一值与之对应,就说x是自变量, y是因变量,有时也称y是x的函数.
自变量:是指在他的取值范围内可以随心所欲的,
自由自在的取它想取的值,看这概念够贴切了吧。
因变量:这个“因”字是指因x的变化,通过一定的
关系而得到的。 在问题①中,t 是自变量,T是因变量。
在问题②中,x是自变量,y是因变量。
在问题③中,l是自变量,f是因变量。
在问题④中,r是自变量, S是因变量。
“y有唯一值与之对应”是指在自变量的取值范围内,x每取一个确定的值,y都有唯一的值与之对应,否则y不是x的函数;例 下列关系中,y不是x的函数的有:不是每一种函数关系都可以用代数式表示
出来的,通常表示函数关系的方法有三种:
1、图像法,如问题1;
2、列表法,如问题2和问题3中的列表;
3、解析法,即列出函数关系的解析式,
如问题3和问题4 。
当然对于同一个函数也可以选择不同的
函数表达关系式。在有些问题中,还有一些量它的数值始终都保持不变,
这样的量称为常量.如问题3中300000,
问题4中的π 练 习(1)从表中你能看出该市14岁的男学生的平均身高是多少吗?
(2)该市男学生的平均身高从哪一岁开始迅速增加?
(3)上表反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?2.解:2.下表是某市2000年统计的该市男学生各年龄组的平均身高.1.举3个日常生活中遇到的函数关系的例子.(1) 14岁的男学生的平均身高是146.1cm. (2)约从11岁开始身高迅速增加.(3) 反映了该市男学生的平均身高和年龄这两个变量之间的关系,其中年龄是自变量,平均身高是因变量.3.写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)火车以90千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.3.解:(2) s=90t, S=(n-2) ×180, (1)C=2?r, 2、 ?是常量,r和C是变量. 90是常量,t和s是变量.2和180是常量, n和S是变量.(1).一辆汽车以40千米/小时的速度行驶,写出行驶路程s(千米)与行驶时间t(时)的关系式。 解:S=40t 其中t是自变量,S是因变量
40是常量(2).一辆汽车行驶5小时,写出行驶路程s
(千米)与行驶速度v(千米/小时)之间的关系式 解:S=5V 其中V是自变量,S是因变量
5是常量练习二写出下列各问题中的关系式,并指出其中
的自变量,因变量和常量(3)三角形的其中两边分别为2,4,
则三角形第三边x与三角形的周长y之间的关系 解: y =6+ x ,其中x是自变量,
y是因变量6是常量练习三某电信公司手机的A类收费标准如下:不管通话时间
多长、每部手机必须缴月租50元外,每通话1分交费0.4元。(1)写出每月应缴费用y(元)和通话时间x(分)之间的关系式; ?(2)某手机用户这个月通话时间为152分,他应缴费多少元?(3)如果一手机用户本月交了200元的费用,他通话的时间是多少分钟? 解:(1)y=50+0.4x(2)当x=152时,y=50+152×0.4=110.8(元)(3)当y=200时,200=50+0.4x,
解这个方程得x=375(分)答:略小结:一 常量与变量 在某一变化过程中,可以取不同数值的量,叫做变量. 在研究问题的过程中,取值始终保持不变的量,叫做常量.二 函数函数的定义: 如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数. 作业习题18.1的 1.
