18.3.3一次函数的性质课件(广西壮族自治区防城港市防城区)
文档属性
| 名称 | 18.3.3一次函数的性质课件(广西壮族自治区防城港市防城区) |  | |
| 格式 | rar | ||
| 文件大小 | 277.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-29 13:19:00 | ||
图片预览






文档简介
课件22张PPT。18.3.3一次函数的性质(1)
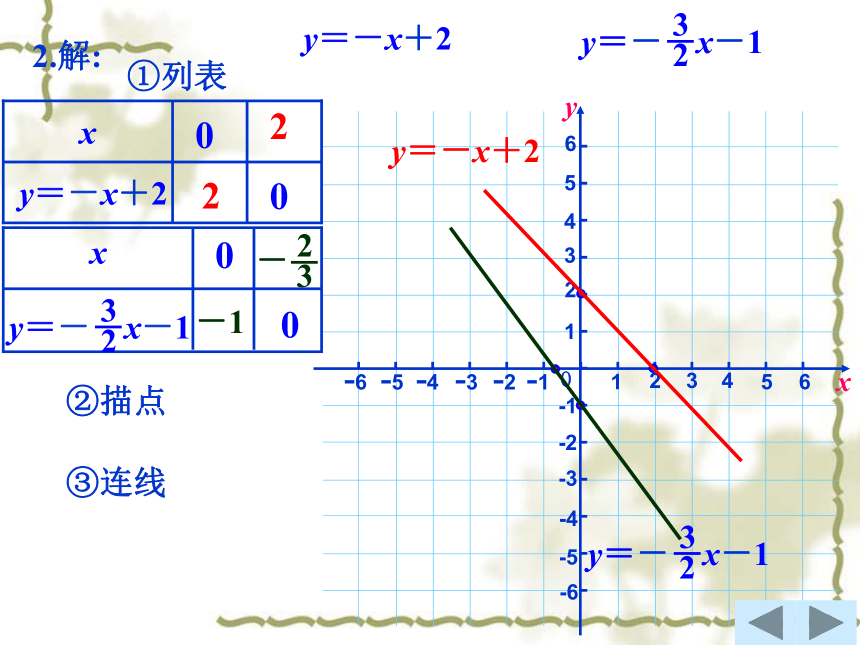
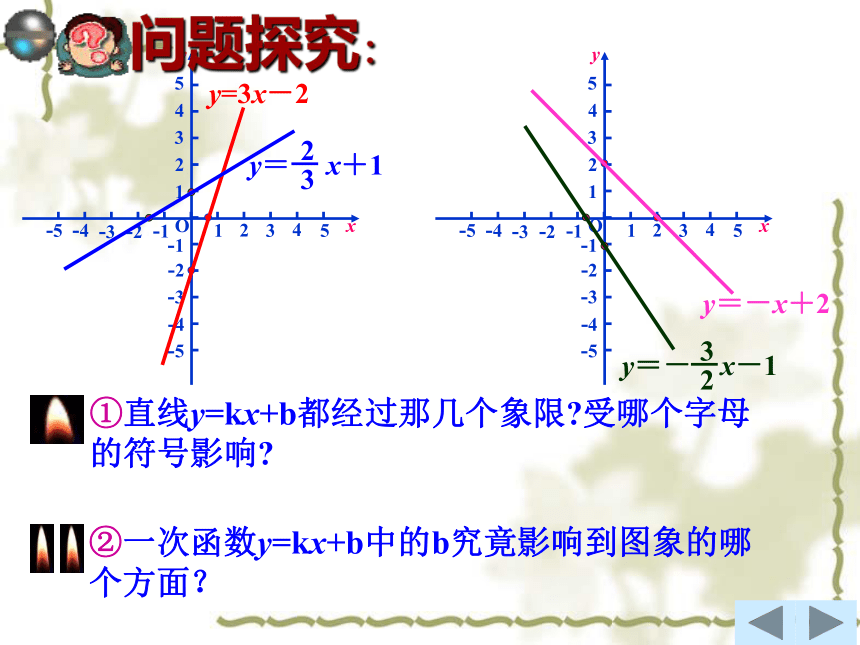
1.一次函数的一般式.y=kx+b(k,b为常数,k≠0)说一说:2.一次函数的图象是什么?一条直线.3.一次函数又有什么性质呢? 这节课我们要借助函数图象研究一次函数的性质.我们先来看下面的问题:1.在同一直角坐标系中画出下列函数的图像:y=3x-2和2.在同一直角坐标系中画出下列函数的图像:y=-x+2和y=3x-21.解:①列表②描点③连线-21y=3x-22.解:①列表②描点③连线2-12y=-x+2y=-x+2④当自变量x从小到大逐渐增大时,对应的函数值y有何变化?如x=-1,x=0,x=2, x=3时,对应的y值分别为多少?⑤在你们所画的两条直线中,请你再比较一下,当k都取正值或都取负值时,哪条直线与x轴正方向所夹的角更大呢?你能得出什么规律呢?x增大y增大(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;函数y=3x-2的图象(右图中虚线)是否也有这种现象呢? 在函数 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从低到高变化(函数y的值也从小变到大).x增大y减小(2) 当k<0时,y随x的
增大而_____,这时函数
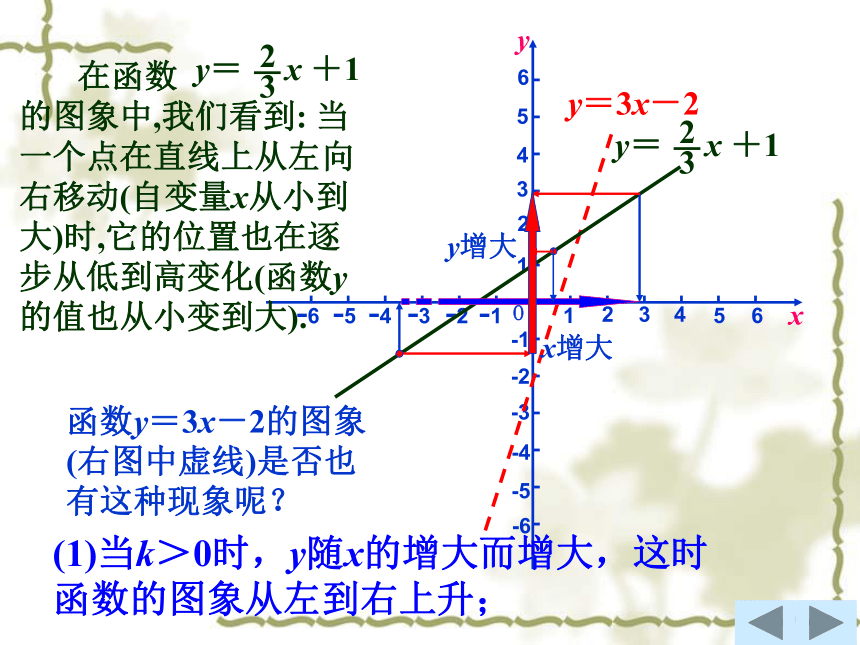
的图象从左到右_____. 减小下降函数 的图象(右图中虚线)是否也有这种现象呢? 在函数y=-x+2 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从高到低变化(函数y的值也从大变到小).一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而增大,这时函数的图象随着自变量x的增大而从左到右上升;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象随着自变量x的增大而从左到右_____. 概括减小下降一次函数的性质图 象*k越小直线相对于x轴越陡峭. *k越大直线相对于x轴越陡峭. 图象与y轴相交于负半轴,图象只经过二、三、四象限,不经过第一象限. 图象与y轴相交于正半轴,图象只经过一、二、四象限,不经过第三象限. 图象与y轴相交于负半轴,图象只经过一、三、四象限,不经过第二象限.图象与y轴相交于正半轴,图象只经过一、二、三象限,不经过第四象限. 函数的图象随着x的增大从左到右下降. 函数的图象随着x的增大从左到右上升 .y随x的增大而减小 y随x的增大而增大 一
次
函
数
的
性
质 b<0b>0b<0b>0y=kx+b (k≠0)一次函数关系式k>0k<0 (4) 函数的图象不经过哪个象限?画出函数y=-2x+2 的图象,结合图象回答下列问题:(1)这个函数中,随着x的增大,y将增大还是减小?它的图象从左到右怎样变化?(2)当x取何值时,y=0?当y取何值时,x=0?(3)当x取何值时,y>0?做一做 当k<0时,y随x的
增大而_____,这时函数
的图象从左到右_____. 减小下降1.解:①列表②描点③连线2y=-2x+21(1) 这个函数中,随着x的增大,y减小,它的图象从左到右下降.(2) 由图象可得当 x<1 时 y> 0.(3) 由图象可得(4) 函数的图象不经过第三个象限.当 x=1时 y=0 ,当 y=2时 x =0 解:(1) 这个函数中,随着x的增大,y减小,它的图象从左到右下降.y=-2x+2(2) ∵ y=0 ,∴当 x<1 时 y> 0.x < 1∴-2x+2=0 , x=1∵ x=0 ,∴y=-2×0+2=2(3) ∵ y>0 ,∴-2x+2>0 , (4) 函数的图象不经过第三个象限.∴当 x=1时 y=0 ,当 y=2时 x =0 试一试 下列一次函数中,y的值随x的增大而减小
的有________. (1)、(3)(1) y=-2x-1(2) y=3x+2(3) y=4-x(4) y=5x-11.一次函数y=kx+b中,kb>0,且y随x的增大而
减小,画出的大致图象为( ).2. 写出m的3个值,使相应的一次函数
y = (2m-1)x+2的值都是随x的增大而增大CDCBA拓展与应用 2.函数y=2-3x,y随x的增大而______ .3.直线y=3x-5与直线y=3x+7的位置关系______.4.直线y=2x-6与直线y=-x-6的位置关系______.增大减小平行相交课堂练习:1.函数y=-3+5x,y随x的增大而________.例1 已知一次函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
(2)当 m取何值时,y随x的增大而减小?解:(1)当m+1>0即m>-1时,y随x的增大而增大;(2)当m+1<0即m<-1时,y随x的增大而减小.例2 已知点(2,m)、(-3,n)都在直线 上,试比较 m和n的大小.你能想出几种判断的方法?所以函数y随x增大而增大 .解: 方法一 把两点的坐标代入函数关系式当 x=2 时, m=当 x=-3 时, n=所以 m > n .方法二 因为 k=> 0,从而直接得到 m > n . 2.已知点(-1,a)和( ,b)都在直线 y= x+3 上,试比较a和b的大小.1.已知函数y= (m-3)x-(1)当m取何值时y随x 的增大而增大?
(2)当m取何值时y随x 的增大而减小?练习1.直接代入计算.2.根据性质判断.3.通过图像判断.已知一次函数 y=kx+b (k≠0);
①如果函数的图象只经过第二、三、四象限,请你试着确定k和b的符号;
②如果函数的图象不经过第一象限,请你试着确定k和b的符号。思考①函数图象与y轴交点是(0,b),
与x轴交点是(- ,0).
②当k>0,b>0时,函数图象过一、二、三象限,
y随x的增大而增大;
③当k>0,b<0时,函数图象过一、三、四象限,
y随x的增大而增大;
④当k>0,b=0时,函数图象过一、三象限,
y随x的增大而增大;
⑤当k<0,b>0时,函数图象过一、二、四象限,
y随x的增大而减小;
⑥当k<0,b<0时,函数图象过二、三、四象限,
y随x的增大而减小;
⑦当k<0,b=0时,函数图象过二、四象限,
y随x的增大而减小.经过本节课的学习,你有哪些收获?
1.一次函数的一般式.y=kx+b(k,b为常数,k≠0)说一说:2.一次函数的图象是什么?一条直线.3.一次函数又有什么性质呢? 这节课我们要借助函数图象研究一次函数的性质.我们先来看下面的问题:1.在同一直角坐标系中画出下列函数的图像:y=3x-2和2.在同一直角坐标系中画出下列函数的图像:y=-x+2和y=3x-21.解:①列表②描点③连线-21y=3x-22.解:①列表②描点③连线2-12y=-x+2y=-x+2④当自变量x从小到大逐渐增大时,对应的函数值y有何变化?如x=-1,x=0,x=2, x=3时,对应的y值分别为多少?⑤在你们所画的两条直线中,请你再比较一下,当k都取正值或都取负值时,哪条直线与x轴正方向所夹的角更大呢?你能得出什么规律呢?x增大y增大(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;函数y=3x-2的图象(右图中虚线)是否也有这种现象呢? 在函数 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从低到高变化(函数y的值也从小变到大).x增大y减小(2) 当k<0时,y随x的
增大而_____,这时函数
的图象从左到右_____. 减小下降函数 的图象(右图中虚线)是否也有这种现象呢? 在函数y=-x+2 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从高到低变化(函数y的值也从大变到小).一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而增大,这时函数的图象随着自变量x的增大而从左到右上升;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象随着自变量x的增大而从左到右_____. 概括减小下降一次函数的性质图 象*k越小直线相对于x轴越陡峭. *k越大直线相对于x轴越陡峭. 图象与y轴相交于负半轴,图象只经过二、三、四象限,不经过第一象限. 图象与y轴相交于正半轴,图象只经过一、二、四象限,不经过第三象限. 图象与y轴相交于负半轴,图象只经过一、三、四象限,不经过第二象限.图象与y轴相交于正半轴,图象只经过一、二、三象限,不经过第四象限. 函数的图象随着x的增大从左到右下降. 函数的图象随着x的增大从左到右上升 .y随x的增大而减小 y随x的增大而增大 一
次
函
数
的
性
质 b<0b>0b<0b>0y=kx+b (k≠0)一次函数关系式k>0k<0 (4) 函数的图象不经过哪个象限?画出函数y=-2x+2 的图象,结合图象回答下列问题:(1)这个函数中,随着x的增大,y将增大还是减小?它的图象从左到右怎样变化?(2)当x取何值时,y=0?当y取何值时,x=0?(3)当x取何值时,y>0?做一做 当k<0时,y随x的
增大而_____,这时函数
的图象从左到右_____. 减小下降1.解:①列表②描点③连线2y=-2x+21(1) 这个函数中,随着x的增大,y减小,它的图象从左到右下降.(2) 由图象可得当 x<1 时 y> 0.(3) 由图象可得(4) 函数的图象不经过第三个象限.当 x=1时 y=0 ,当 y=2时 x =0 解:(1) 这个函数中,随着x的增大,y减小,它的图象从左到右下降.y=-2x+2(2) ∵ y=0 ,∴当 x<1 时 y> 0.x < 1∴-2x+2=0 , x=1∵ x=0 ,∴y=-2×0+2=2(3) ∵ y>0 ,∴-2x+2>0 , (4) 函数的图象不经过第三个象限.∴当 x=1时 y=0 ,当 y=2时 x =0 试一试 下列一次函数中,y的值随x的增大而减小
的有________. (1)、(3)(1) y=-2x-1(2) y=3x+2(3) y=4-x(4) y=5x-11.一次函数y=kx+b中,kb>0,且y随x的增大而
减小,画出的大致图象为( ).2. 写出m的3个值,使相应的一次函数
y = (2m-1)x+2的值都是随x的增大而增大CDCBA拓展与应用 2.函数y=2-3x,y随x的增大而______ .3.直线y=3x-5与直线y=3x+7的位置关系______.4.直线y=2x-6与直线y=-x-6的位置关系______.增大减小平行相交课堂练习:1.函数y=-3+5x,y随x的增大而________.例1 已知一次函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
(2)当 m取何值时,y随x的增大而减小?解:(1)当m+1>0即m>-1时,y随x的增大而增大;(2)当m+1<0即m<-1时,y随x的增大而减小.例2 已知点(2,m)、(-3,n)都在直线 上,试比较 m和n的大小.你能想出几种判断的方法?所以函数y随x增大而增大 .解: 方法一 把两点的坐标代入函数关系式当 x=2 时, m=当 x=-3 时, n=所以 m > n .方法二 因为 k=> 0,从而直接得到 m > n . 2.已知点(-1,a)和( ,b)都在直线 y= x+3 上,试比较a和b的大小.1.已知函数y= (m-3)x-(1)当m取何值时y随x 的增大而增大?
(2)当m取何值时y随x 的增大而减小?练习1.直接代入计算.2.根据性质判断.3.通过图像判断.已知一次函数 y=kx+b (k≠0);
①如果函数的图象只经过第二、三、四象限,请你试着确定k和b的符号;
②如果函数的图象不经过第一象限,请你试着确定k和b的符号。思考①函数图象与y轴交点是(0,b),
与x轴交点是(- ,0).
②当k>0,b>0时,函数图象过一、二、三象限,
y随x的增大而增大;
③当k>0,b<0时,函数图象过一、三、四象限,
y随x的增大而增大;
④当k>0,b=0时,函数图象过一、三象限,
y随x的增大而增大;
⑤当k<0,b>0时,函数图象过一、二、四象限,
y随x的增大而减小;
⑥当k<0,b<0时,函数图象过二、三、四象限,
y随x的增大而减小;
⑦当k<0,b=0时,函数图象过二、四象限,
y随x的增大而减小.经过本节课的学习,你有哪些收获?
