思维拓展:探索规律-数学五年级上册苏教版(含解析)
文档属性
| 名称 | 思维拓展:探索规律-数学五年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 18:56:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
思维拓展:探索规律-数学五年级上册苏教版
一、选择题
1.循环小数的小数点后面第30位上的数字是( )。
A.7 B.5 C.2
2.把长2cm,宽1cm的长方形一层、二层、三层…有规律地摆下去(如图),摆到第十层时,这个图形的面积是( )cm2。
A.20 B.110 C.100 D.90
3.已知1÷11=0.0909…,2÷11=0.1818…,3÷11=0.2727…,那么:13÷11=( )。
A.1.1717… B.1.1818 C.1.1717 D.
4.用同样大小的黑色棋子按如图所示的规律摆放,第1个图形有6枚棋子,第2个图形有9枚棋子,第3个图形有12枚棋子,第4个图形有15枚棋子,……,以此类推,第7个图形有( )枚棋子。
A.18 B.21 C.24 D.27
5.不计算,请你根据规律选出得数。
6.6666×6666.7=( )
A.4444.2222 B.4444.2222 C.44444.22222
6.将按右面的方式摆放在桌面上:继续按这种方式摆放,6个有( )个面露在外面。
A.29 B.26 C.23 D.20
二、填空题
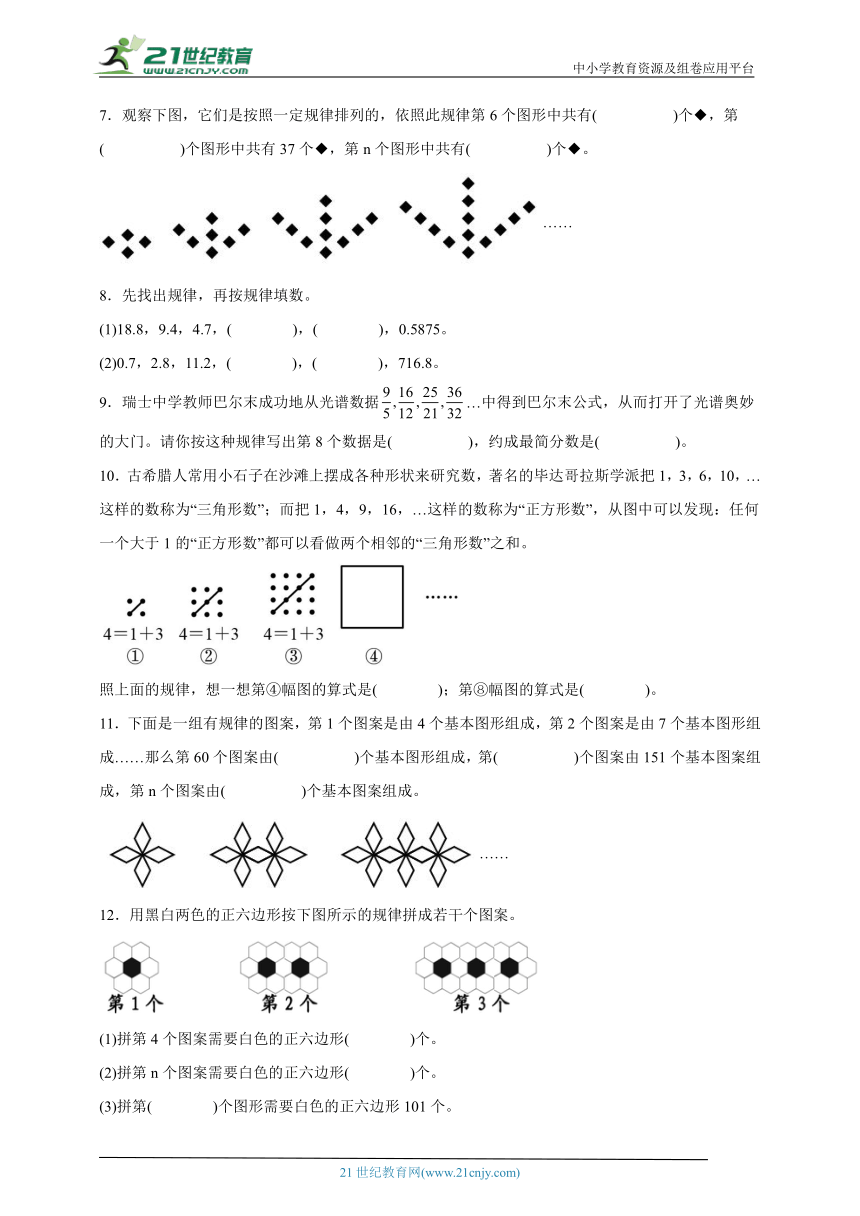
7.观察下图,它们是按照一定规律排列的,依照此规律第6个图形中共有( )个◆,第( )个图形中共有37个◆,第n个图形中共有( )个◆。
……
8.先找出规律,再按规律填数。
(1)18.8,9.4,4.7,( ),( ),0.5875。
(2)0.7,2.8,11.2,( ),( ),716.8。
9.瑞士中学教师巴尔末成功地从光谱数据…中得到巴尔末公式,从而打开了光谱奥妙的大门。请你按这种规律写出第8个数据是( ),约成最简分数是( )。
10.古希腊人常用小石子在沙滩上摆成各种形状来研究数,著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”;而把1,4,9,16,…这样的数称为“正方形数”,从图中可以发现:任何一个大于1的“正方形数”都可以看做两个相邻的“三角形数”之和。
照上面的规律,想一想第④幅图的算式是( );第⑧幅图的算式是( )。
11.下面是一组有规律的图案,第1个图案是由4个基本图形组成,第2个图案是由7个基本图形组成……那么第60个图案由( )个基本图形组成,第( )个图案由151个基本图案组成,第n个图案由( )个基本图案组成。
……
12.用黑白两色的正六边形按下图所示的规律拼成若干个图案。
(1)拼第4个图案需要白色的正六边形( )个。
(2)拼第n个图案需要白色的正六边形( )个。
(3)拼第( )个图形需要白色的正六边形101个。
13.观察下图:
……
如果按照上面的样子继续摆下去,第5个图形要用( )朵小花;第个图形要用( )朵小花。
14.按规律填空。
1×0.9+0.2=1.1,12×0.9+0.3=11.1,123×0.9+0.4=111.1,那么( )×0.9+( )=111111.1。
三、解答题
15.一个循环小数是,它的小数部分第2022位上是几?
16.“春晖影视城”贵宾厅一共有8排座位。第一排有12个座位,后面每排都比前面一排多2个座位。这个贵宾厅一共有多少个座位?
17.按照2个红珠子、3个蓝珠子的规律穿一串珠子,第23个珠子应该是什么颜色?
18.有一列数:2,3,6,8,8…,从第三个数算起,每个数都是前两个数乘积的个位数字,那么这列数的第81个数是多少?
19.拼成一个等腰三角形要用5根火柴棒,每条腰用两根,底用一根火柴棒。拼成2个这样的等腰三角形要用8根火柴棒(两个三角形拼在一起),拼成3个这样的等腰三角形要用11根火柴棒,那么拼成n个这样的等腰三角形至少要多少根火柴棒。
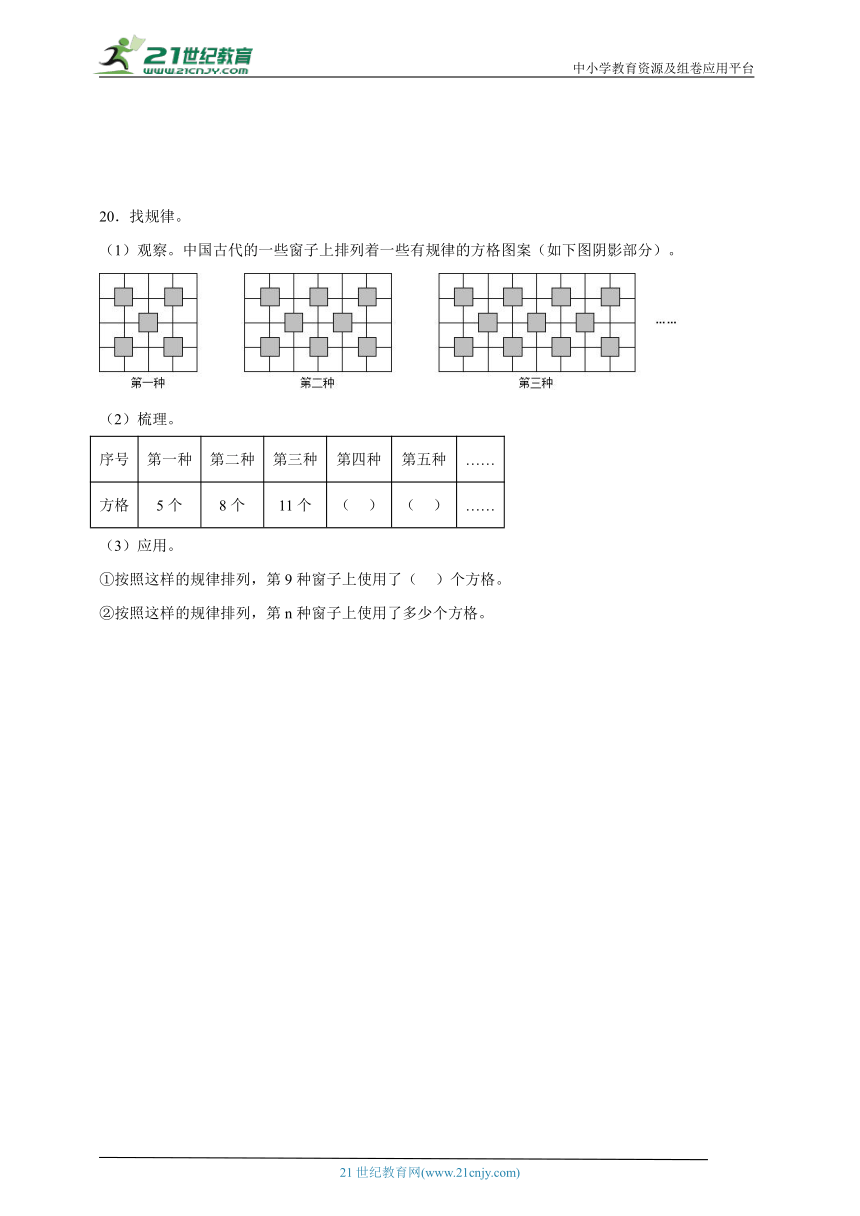
20.找规律。
(1)观察。中国古代的一些窗子上排列着一些有规律的方格图案(如下图阴影部分)。
(2)梳理。
序号 第一种 第二种 第三种 第四种 第五种 ……
方格 5个 8个 11个 ( ) ( ) ……
(3)应用。
①按照这样的规律排列,第9种窗子上使用了( )个方格。
②按照这样的规律排列,第n种窗子上使用了多少个方格。
参考答案:
1.A
【分析】循环小数中小数部分重复出现的数字叫做循环节,重复的几个数字可根据周期性得出答案。
【详解】(30-1)÷3
=29÷3
=9……2,所以第30位上的数字是7;
循环小数的小数点后面第30位上的数字是7。
故答案为:A
【点睛】本题主要考查的是循环小数及周期变化规律,解题的关键是掌握循环小数的循环节,进而得出答案。
2.B
【分析】先根据长方形的面积=长×宽,求出一个长方形的面积,再观察图形,第一层有一个长方形,第二层有两个长方形,第三层有三个长方形,则第几层就有几个长方形,以此类推,把十层长方形的数量相加,求出长方形的总数量,用长方形的总数量乘一个长方形的面积,即可解答。
【详解】2×1=2(cm2)
(1+2+3+4+5+6+7+8+9+10)×2
=(10+1)×(10÷2)×2
=11×5×2
=55×2
=110(cm2)
这个图形的面积是110cm2。
故答案为:B
【点睛】此题属于探索简单图形覆盖现象中的规律问题,考查学生总结规律的能力。
3.D
【分析】观察算式1÷11=0.0909…,2÷11=0.1818…,3÷11=0.2727…,找到规律:都与第一个算式比较,除数都是11,商是循环小数;被除数分别乘2、3……,那么商的循环节09也分别乘2、3……,且循环节的数字相加的和是9;据此写出13÷11的得数。
【详解】已知1÷11=0.0909…,2÷11=0.1818…,3÷11=0.2727…,那么:
13÷11=。
故答案为:D
【点睛】本题考查找规律,观察给出的算式,找到算式的规律,应用发现的规律解决问题是解题的关键。
4.C
【分析】仔细观察可以发现,每一个图形中的棋子数比前一个图形多3个,根据这一规律得出第n个图形中的棋子数为3+3n,据此计算即可得解。
【详解】每一个图形中的棋子数比前一个图形多3个,所以第n个图形中的棋子数为3+3n;
第7个图中有棋子:3+3×7=24(枚)
即第7个图中有24枚黑棋子
故答案为:C
【点睛】本题主要考查数与形结合的规律,发现每一个图形中的棋子数比前一个图形多3个是解本题的关键。
5.C
【分析】通过观察,第一个因数有几个6,得数中就有几个4和几个2,小数点是4和2的分界线;6.6666×6666.7中,第一个因数有5个6,所以得数中就有5个4和5个2,4与2之间点上小数点,据此即可解答。
【详解】由分析可知;6.6666×6666.7=44444.22222。
故答案为:C
【点睛】找出算式的规律,然后根据规律直接写出得数。
6.D
【分析】1个小正体有5个面露在外面,再增加一个正方体,2个小正方体有8个面露在外面;3个小正方体有11个面露在外面.每增加1个正方体漏在外面的面就增加3个即:n个正方体有5+(n-1)×3;由此求解。解答此题应根据题意,进行推导,得出规律:即1个小正方体露出5个面,每增加1个小正方体增加3个面;进行解答即可。
【详解】根据分析可知,6个正方体有:
5+(6-1)×3
=5+5×3
=5+15
=20(个)
故答案为:D
【点睛】解答本题先找出规律,再根据找出的规律进行解答。
7. 19 12 3n+1
【分析】观察可知:◆的个数=第几个图形就用几×3+1,反过来,(◆的个数-1)÷3=第几个图形,据此分析。
【详解】6×3+1
=18+1
=19(个)
(37-1)÷3
=36÷3
=12(个)
n×3+1=(3n+1)个
第6个图形中共有19个◆,第12个图形中共有37个◆,第n个图形中共有(3n+1)个◆。
【点睛】关键是理解字母可以表示任意数,可以用字母将数量关系表示出来。
8.(1) 2.35 1.175
(2) 44.8 179.2
【分析】(1)观察数列可知,前一个数除以2即可得到后一个数,据此计算即可;
(2)观察数列可知,前一个数乘4即可得到后一个数,据此计算即可。
【详解】(1)4.7÷2=2.35
2.35÷2=1.175
则18.8,9.4,4.7,2.35,1.175,0.5875。
(2)11.2×4=44.8
44.8×4=179.2
则0.7,2.8,11.2,44.8,179.2,716.8。
【点睛】本题考查数字的排列规律,发现规律,利用规律是解题的关键。
9.
【分析】先观察分子:9、16、25、36,分别是(1+2)2、(2+2)2、(3+2)2、(4+2)2,据此得出第n个数据的分子是(n+2)2;再观察分母:5、12、21、32,可分别改写成1×5、2×6、3×7、4×8,据此得出第n个数据的分母是n(n+4),接下来将n=8代入即可求出第8个数据。
【详解】根据分析可得规律:
分子是:(1+2)2、(2+2)2、(3+2)2、(4+2)2、…、(n+2)2、…
分母是:1×5、2×6、3×7、4×8、…、n(n+4)、…
所以,第n个数据的分数是:;
所以,第8个数据的分数是:
=
=
=
=
=
所以,按这种规律写出第8个数据是,约成最简分数是。
【点睛】本题考查的是探究规律:数字字母规律问题,应从仔细观察题中所给的已知数据、、、,找到它们的共同特点入手。
10. 25=10+15 81=36+45
【分析】通过题目可知,三角形数是1、3、6、10…,由此即可知道相邻的两个数的差值比前一个相邻的两个数的差值依次多1,正方形数依次是第几个图形的平方,由于第一个图形的正方数是4,即2×2=4,说明④的正方形数应该是52=25,第⑧幅图的正方形数是92=81,再根据三角形数写出相应的数字即可填空。
【详解】由分析可知:
三角形数依次是1、3、6、10、15、21、28、36、45…
第④幅图的算式是:25=10+15;
第⑧幅图的算式是:81=36+45
【点睛】解答本题的关键是找清楚“三角形数”和“正方形数”的关系,从而进行求解。
11. 181 50
【分析】因为第一个图形由4个基本图形组成,即:3×1+1,第二个图形由7个基本图形组成,即:3×2+1,第三个图形由10个基本图形组成,即:3×3+1,所以基本图形的个数与图形的数量的关系:3n+1(n为图形的数量);所以把相应的数量代入以上的关系式,从而求得基本图形的个数和是第多少个图案的解。
【详解】第60个图案:3×60+1=180+1=181;
当3n+1=151,则n=(151-1)÷3=150÷3=50;
第n个图案:3n+1
所以:那么第60个图案由151个基本图形组成,第50个图案由151个基本图案组成,第n个图案由(3n+1)个基本图案组成。
【点睛】本题考查的是物体的排列规律,关键是掌握其中的规律。
12.(1)21
(2)5n+1
(3)20
【分析】(1)观察可知,第几个图形中间就有几个黑色正六边形;第一个图形白色有6个,即6=1×5+1;第二个图形白色有11个,即11=2×5+1,第三个图形有16个,即16=3×5+1,即白色正六边形数量=黑色正六边形的数量×5+1,据此分析。
【详解】(1)4×5+1
=20+1
=21(个)
拼第4个图案需要白色的正六边形21个。
(2)n×5+1=(5n+1)个
拼第n个图案需要白色的正六边形(5n+1)个。
(3)5n+1=101
解:5n+1-1=101-1
5n=100
5n÷5=100÷5
n=20
拼第20个图形需要白色的正六边形101个。
【点睛】本题主要考查数与形,找准图形的变化规律并用字母表示出来,同时熟练掌握等式的性质。
13. 11 2n+1
【分析】观察图形可知,第一个图形要用3朵小花,第二个图形要用5朵小花,第三个图形要用7朵小花,则第n个图形要用(2n+1)朵小花,据此解答即可。
【详解】由分析可知:
第5个图形要用小花的朵数为:
2n+1=2×5+1=11(朵)
如果按照上面的样子继续摆下去,第5个图形要用11朵小花;第个图形要用(2n+1)朵小花。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
14. 123456 0.7
【分析】乘号前面的因数依次是1、12、123…;乘号后面的因数都是0.9;加号后面的数依次是0.2、0.3、0.4…小数点后面的数字比乘号前面因数中数字的个数多1;积都是十分位上为1的一位小数,整数部分1的个数等于乘号前面因数中数字的个数,据此解答。
【详解】分析可知,1×0.9+0.2=1.1,12×0.9+0.3=11.1,123×0.9+0.4=111.1,那么123456×0.9+0.7=111111.1。
【点睛】根据已知算式找出算式变化的规律是解答题目的关键。
15.4
【分析】根据题意可知,从小数点后第1位开始,每4个数字一循环,计算第2022里面有多少个完整的循环节,余数是几,就在循环节里面从左往右数出第几位上的数字,据此解答。
【详解】循环节一共有4个数字。
2022÷4=505……2
循环节的第二个数字是4;它的小数部分第2022位上是4。
答:一个循环小数是,它的小数部分第2022位上是4。
【点睛】先找到规律,再根据规律求解。
16.152个
【分析】根据已知条件,第一排有12个座位,后面每排都比前面一排多2个座位,则:
第二排有:12+1×2=14个;
第三排有:12+2×2=16个;
第四排有:12+3×2=18个;
……
第n排有:12+(n-1)×2;
所以第八排有:12+7×2=26个。
将8排的座位数相加即可求出贵宾厅一共有多少个座位。
【详解】第八排的座位个数:
12+(8-1)×2
=12+14
=26(个)
贵宾厅座位总个数:
12+14+16+18+20+22+24+26
=(12+26)+(14+24)+(16+22)+(18+20)
=38×4
=152(个)
答:这个贵宾厅一共有152个座位。
【点睛】解答本题的关键是根据已知条件,先求出最后一排的个数。
17.蓝色
【分析】按照2个红珠子、3个蓝珠子的规律穿一串珠子,5个珠子为一组,要想知道第23个珠子是什么颜色,只要知道23÷5后的余数是几,然后分析即可。
【详解】23÷5=4(组)……3(个)
答:第23个珠子应该是蓝色。
【点睛】本题考查简单周期现象中的排列规律,利用有余数的除法解决生活实际问题,余数是几,答案就是一组中的第几个。如果没有余数,则正好是一组中的最后一个。
18.6
【分析】根据题意,从第三个数起,每个数都是前两个数的乘积的个位数字,可得到这样一串数:2,3,6,8,8,4,2,8,6,8,8,4,2,8,6…。除去前两个数,后面的数按6,8,8,4,2,8的周期排列;循环周期为6,由于该数列前面两个数字不符合规则,用81减去2,再除以6,余数就在循环周期中数几,即可解答。
【详解】(81-2)÷6
=79÷6
=13(组)……1
第81个数是6。
答:这列数的第81个数是6。
【点睛】本题考查周期问题,关键是找到规律,确定周期;用总量除以周期,进行解答。
19.(3n+2)根
【分析】由题意可知,第一个等腰三角形用了5=2×2+1根火柴棒,第二个等腰三角形用了8=2×3+2根火柴棒,第三个等腰三角形用了11=2×4+3根火柴棒,…,由此得出第n个等腰三角形用了2×(n+1)+n根火柴棒,据此解答
【详解】第一个等腰三角形用了5=2×2+1根火柴棒,
第二个等腰三角形用了8=2×3+2根火柴棒,
第三个等腰三角形用了11=2×4+3根火柴棒,…
所以,第n个等腰三角形用了2×(n+1)+n=3n+2根火柴棒;
答:拼成n个这样的等腰三角形至少要(3n+2)根火柴棒。
【点睛】此题主要考查了图形的变化规律,注意结合图形发现蕴含的运算规律,找出解决问题的途径。
20.(2)14;17;(3)①29;② 3n+2
【分析】观察窗子上排列的方格图案,找到规律,从而进行推导得出答案。
【详解】(2)第一种有3×1+2=5个方格;
第二种有3×2+2=8个方格;
第三种有3×3+2=11个方格;
第n种则有(3n+2)个方格;
第四种则有3×4+2=14个方格;
第五种则有3×5+2=17个方格。
(3)①按照这样的规律排列,第9种窗子上使用了3×9+2=29个方格。
②按照这样的规律排列,第n种窗子上使用了(3n+2)个方格。
【点睛】本题考查图形的变化类为题,重点考查了学生通过观察、归纳、抽象出数的规律的能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:探索规律-数学五年级上册苏教版
一、选择题
1.循环小数的小数点后面第30位上的数字是( )。
A.7 B.5 C.2
2.把长2cm,宽1cm的长方形一层、二层、三层…有规律地摆下去(如图),摆到第十层时,这个图形的面积是( )cm2。
A.20 B.110 C.100 D.90
3.已知1÷11=0.0909…,2÷11=0.1818…,3÷11=0.2727…,那么:13÷11=( )。
A.1.1717… B.1.1818 C.1.1717 D.
4.用同样大小的黑色棋子按如图所示的规律摆放,第1个图形有6枚棋子,第2个图形有9枚棋子,第3个图形有12枚棋子,第4个图形有15枚棋子,……,以此类推,第7个图形有( )枚棋子。
A.18 B.21 C.24 D.27
5.不计算,请你根据规律选出得数。
6.6666×6666.7=( )
A.4444.2222 B.4444.2222 C.44444.22222
6.将按右面的方式摆放在桌面上:继续按这种方式摆放,6个有( )个面露在外面。
A.29 B.26 C.23 D.20
二、填空题
7.观察下图,它们是按照一定规律排列的,依照此规律第6个图形中共有( )个◆,第( )个图形中共有37个◆,第n个图形中共有( )个◆。
……
8.先找出规律,再按规律填数。
(1)18.8,9.4,4.7,( ),( ),0.5875。
(2)0.7,2.8,11.2,( ),( ),716.8。
9.瑞士中学教师巴尔末成功地从光谱数据…中得到巴尔末公式,从而打开了光谱奥妙的大门。请你按这种规律写出第8个数据是( ),约成最简分数是( )。
10.古希腊人常用小石子在沙滩上摆成各种形状来研究数,著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”;而把1,4,9,16,…这样的数称为“正方形数”,从图中可以发现:任何一个大于1的“正方形数”都可以看做两个相邻的“三角形数”之和。
照上面的规律,想一想第④幅图的算式是( );第⑧幅图的算式是( )。
11.下面是一组有规律的图案,第1个图案是由4个基本图形组成,第2个图案是由7个基本图形组成……那么第60个图案由( )个基本图形组成,第( )个图案由151个基本图案组成,第n个图案由( )个基本图案组成。
……
12.用黑白两色的正六边形按下图所示的规律拼成若干个图案。
(1)拼第4个图案需要白色的正六边形( )个。
(2)拼第n个图案需要白色的正六边形( )个。
(3)拼第( )个图形需要白色的正六边形101个。
13.观察下图:
……
如果按照上面的样子继续摆下去,第5个图形要用( )朵小花;第个图形要用( )朵小花。
14.按规律填空。
1×0.9+0.2=1.1,12×0.9+0.3=11.1,123×0.9+0.4=111.1,那么( )×0.9+( )=111111.1。
三、解答题
15.一个循环小数是,它的小数部分第2022位上是几?
16.“春晖影视城”贵宾厅一共有8排座位。第一排有12个座位,后面每排都比前面一排多2个座位。这个贵宾厅一共有多少个座位?
17.按照2个红珠子、3个蓝珠子的规律穿一串珠子,第23个珠子应该是什么颜色?
18.有一列数:2,3,6,8,8…,从第三个数算起,每个数都是前两个数乘积的个位数字,那么这列数的第81个数是多少?
19.拼成一个等腰三角形要用5根火柴棒,每条腰用两根,底用一根火柴棒。拼成2个这样的等腰三角形要用8根火柴棒(两个三角形拼在一起),拼成3个这样的等腰三角形要用11根火柴棒,那么拼成n个这样的等腰三角形至少要多少根火柴棒。
20.找规律。
(1)观察。中国古代的一些窗子上排列着一些有规律的方格图案(如下图阴影部分)。
(2)梳理。
序号 第一种 第二种 第三种 第四种 第五种 ……
方格 5个 8个 11个 ( ) ( ) ……
(3)应用。
①按照这样的规律排列,第9种窗子上使用了( )个方格。
②按照这样的规律排列,第n种窗子上使用了多少个方格。
参考答案:
1.A
【分析】循环小数中小数部分重复出现的数字叫做循环节,重复的几个数字可根据周期性得出答案。
【详解】(30-1)÷3
=29÷3
=9……2,所以第30位上的数字是7;
循环小数的小数点后面第30位上的数字是7。
故答案为:A
【点睛】本题主要考查的是循环小数及周期变化规律,解题的关键是掌握循环小数的循环节,进而得出答案。
2.B
【分析】先根据长方形的面积=长×宽,求出一个长方形的面积,再观察图形,第一层有一个长方形,第二层有两个长方形,第三层有三个长方形,则第几层就有几个长方形,以此类推,把十层长方形的数量相加,求出长方形的总数量,用长方形的总数量乘一个长方形的面积,即可解答。
【详解】2×1=2(cm2)
(1+2+3+4+5+6+7+8+9+10)×2
=(10+1)×(10÷2)×2
=11×5×2
=55×2
=110(cm2)
这个图形的面积是110cm2。
故答案为:B
【点睛】此题属于探索简单图形覆盖现象中的规律问题,考查学生总结规律的能力。
3.D
【分析】观察算式1÷11=0.0909…,2÷11=0.1818…,3÷11=0.2727…,找到规律:都与第一个算式比较,除数都是11,商是循环小数;被除数分别乘2、3……,那么商的循环节09也分别乘2、3……,且循环节的数字相加的和是9;据此写出13÷11的得数。
【详解】已知1÷11=0.0909…,2÷11=0.1818…,3÷11=0.2727…,那么:
13÷11=。
故答案为:D
【点睛】本题考查找规律,观察给出的算式,找到算式的规律,应用发现的规律解决问题是解题的关键。
4.C
【分析】仔细观察可以发现,每一个图形中的棋子数比前一个图形多3个,根据这一规律得出第n个图形中的棋子数为3+3n,据此计算即可得解。
【详解】每一个图形中的棋子数比前一个图形多3个,所以第n个图形中的棋子数为3+3n;
第7个图中有棋子:3+3×7=24(枚)
即第7个图中有24枚黑棋子
故答案为:C
【点睛】本题主要考查数与形结合的规律,发现每一个图形中的棋子数比前一个图形多3个是解本题的关键。
5.C
【分析】通过观察,第一个因数有几个6,得数中就有几个4和几个2,小数点是4和2的分界线;6.6666×6666.7中,第一个因数有5个6,所以得数中就有5个4和5个2,4与2之间点上小数点,据此即可解答。
【详解】由分析可知;6.6666×6666.7=44444.22222。
故答案为:C
【点睛】找出算式的规律,然后根据规律直接写出得数。
6.D
【分析】1个小正体有5个面露在外面,再增加一个正方体,2个小正方体有8个面露在外面;3个小正方体有11个面露在外面.每增加1个正方体漏在外面的面就增加3个即:n个正方体有5+(n-1)×3;由此求解。解答此题应根据题意,进行推导,得出规律:即1个小正方体露出5个面,每增加1个小正方体增加3个面;进行解答即可。
【详解】根据分析可知,6个正方体有:
5+(6-1)×3
=5+5×3
=5+15
=20(个)
故答案为:D
【点睛】解答本题先找出规律,再根据找出的规律进行解答。
7. 19 12 3n+1
【分析】观察可知:◆的个数=第几个图形就用几×3+1,反过来,(◆的个数-1)÷3=第几个图形,据此分析。
【详解】6×3+1
=18+1
=19(个)
(37-1)÷3
=36÷3
=12(个)
n×3+1=(3n+1)个
第6个图形中共有19个◆,第12个图形中共有37个◆,第n个图形中共有(3n+1)个◆。
【点睛】关键是理解字母可以表示任意数,可以用字母将数量关系表示出来。
8.(1) 2.35 1.175
(2) 44.8 179.2
【分析】(1)观察数列可知,前一个数除以2即可得到后一个数,据此计算即可;
(2)观察数列可知,前一个数乘4即可得到后一个数,据此计算即可。
【详解】(1)4.7÷2=2.35
2.35÷2=1.175
则18.8,9.4,4.7,2.35,1.175,0.5875。
(2)11.2×4=44.8
44.8×4=179.2
则0.7,2.8,11.2,44.8,179.2,716.8。
【点睛】本题考查数字的排列规律,发现规律,利用规律是解题的关键。
9.
【分析】先观察分子:9、16、25、36,分别是(1+2)2、(2+2)2、(3+2)2、(4+2)2,据此得出第n个数据的分子是(n+2)2;再观察分母:5、12、21、32,可分别改写成1×5、2×6、3×7、4×8,据此得出第n个数据的分母是n(n+4),接下来将n=8代入即可求出第8个数据。
【详解】根据分析可得规律:
分子是:(1+2)2、(2+2)2、(3+2)2、(4+2)2、…、(n+2)2、…
分母是:1×5、2×6、3×7、4×8、…、n(n+4)、…
所以,第n个数据的分数是:;
所以,第8个数据的分数是:
=
=
=
=
=
所以,按这种规律写出第8个数据是,约成最简分数是。
【点睛】本题考查的是探究规律:数字字母规律问题,应从仔细观察题中所给的已知数据、、、,找到它们的共同特点入手。
10. 25=10+15 81=36+45
【分析】通过题目可知,三角形数是1、3、6、10…,由此即可知道相邻的两个数的差值比前一个相邻的两个数的差值依次多1,正方形数依次是第几个图形的平方,由于第一个图形的正方数是4,即2×2=4,说明④的正方形数应该是52=25,第⑧幅图的正方形数是92=81,再根据三角形数写出相应的数字即可填空。
【详解】由分析可知:
三角形数依次是1、3、6、10、15、21、28、36、45…
第④幅图的算式是:25=10+15;
第⑧幅图的算式是:81=36+45
【点睛】解答本题的关键是找清楚“三角形数”和“正方形数”的关系,从而进行求解。
11. 181 50
【分析】因为第一个图形由4个基本图形组成,即:3×1+1,第二个图形由7个基本图形组成,即:3×2+1,第三个图形由10个基本图形组成,即:3×3+1,所以基本图形的个数与图形的数量的关系:3n+1(n为图形的数量);所以把相应的数量代入以上的关系式,从而求得基本图形的个数和是第多少个图案的解。
【详解】第60个图案:3×60+1=180+1=181;
当3n+1=151,则n=(151-1)÷3=150÷3=50;
第n个图案:3n+1
所以:那么第60个图案由151个基本图形组成,第50个图案由151个基本图案组成,第n个图案由(3n+1)个基本图案组成。
【点睛】本题考查的是物体的排列规律,关键是掌握其中的规律。
12.(1)21
(2)5n+1
(3)20
【分析】(1)观察可知,第几个图形中间就有几个黑色正六边形;第一个图形白色有6个,即6=1×5+1;第二个图形白色有11个,即11=2×5+1,第三个图形有16个,即16=3×5+1,即白色正六边形数量=黑色正六边形的数量×5+1,据此分析。
【详解】(1)4×5+1
=20+1
=21(个)
拼第4个图案需要白色的正六边形21个。
(2)n×5+1=(5n+1)个
拼第n个图案需要白色的正六边形(5n+1)个。
(3)5n+1=101
解:5n+1-1=101-1
5n=100
5n÷5=100÷5
n=20
拼第20个图形需要白色的正六边形101个。
【点睛】本题主要考查数与形,找准图形的变化规律并用字母表示出来,同时熟练掌握等式的性质。
13. 11 2n+1
【分析】观察图形可知,第一个图形要用3朵小花,第二个图形要用5朵小花,第三个图形要用7朵小花,则第n个图形要用(2n+1)朵小花,据此解答即可。
【详解】由分析可知:
第5个图形要用小花的朵数为:
2n+1=2×5+1=11(朵)
如果按照上面的样子继续摆下去,第5个图形要用11朵小花;第个图形要用(2n+1)朵小花。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
14. 123456 0.7
【分析】乘号前面的因数依次是1、12、123…;乘号后面的因数都是0.9;加号后面的数依次是0.2、0.3、0.4…小数点后面的数字比乘号前面因数中数字的个数多1;积都是十分位上为1的一位小数,整数部分1的个数等于乘号前面因数中数字的个数,据此解答。
【详解】分析可知,1×0.9+0.2=1.1,12×0.9+0.3=11.1,123×0.9+0.4=111.1,那么123456×0.9+0.7=111111.1。
【点睛】根据已知算式找出算式变化的规律是解答题目的关键。
15.4
【分析】根据题意可知,从小数点后第1位开始,每4个数字一循环,计算第2022里面有多少个完整的循环节,余数是几,就在循环节里面从左往右数出第几位上的数字,据此解答。
【详解】循环节一共有4个数字。
2022÷4=505……2
循环节的第二个数字是4;它的小数部分第2022位上是4。
答:一个循环小数是,它的小数部分第2022位上是4。
【点睛】先找到规律,再根据规律求解。
16.152个
【分析】根据已知条件,第一排有12个座位,后面每排都比前面一排多2个座位,则:
第二排有:12+1×2=14个;
第三排有:12+2×2=16个;
第四排有:12+3×2=18个;
……
第n排有:12+(n-1)×2;
所以第八排有:12+7×2=26个。
将8排的座位数相加即可求出贵宾厅一共有多少个座位。
【详解】第八排的座位个数:
12+(8-1)×2
=12+14
=26(个)
贵宾厅座位总个数:
12+14+16+18+20+22+24+26
=(12+26)+(14+24)+(16+22)+(18+20)
=38×4
=152(个)
答:这个贵宾厅一共有152个座位。
【点睛】解答本题的关键是根据已知条件,先求出最后一排的个数。
17.蓝色
【分析】按照2个红珠子、3个蓝珠子的规律穿一串珠子,5个珠子为一组,要想知道第23个珠子是什么颜色,只要知道23÷5后的余数是几,然后分析即可。
【详解】23÷5=4(组)……3(个)
答:第23个珠子应该是蓝色。
【点睛】本题考查简单周期现象中的排列规律,利用有余数的除法解决生活实际问题,余数是几,答案就是一组中的第几个。如果没有余数,则正好是一组中的最后一个。
18.6
【分析】根据题意,从第三个数起,每个数都是前两个数的乘积的个位数字,可得到这样一串数:2,3,6,8,8,4,2,8,6,8,8,4,2,8,6…。除去前两个数,后面的数按6,8,8,4,2,8的周期排列;循环周期为6,由于该数列前面两个数字不符合规则,用81减去2,再除以6,余数就在循环周期中数几,即可解答。
【详解】(81-2)÷6
=79÷6
=13(组)……1
第81个数是6。
答:这列数的第81个数是6。
【点睛】本题考查周期问题,关键是找到规律,确定周期;用总量除以周期,进行解答。
19.(3n+2)根
【分析】由题意可知,第一个等腰三角形用了5=2×2+1根火柴棒,第二个等腰三角形用了8=2×3+2根火柴棒,第三个等腰三角形用了11=2×4+3根火柴棒,…,由此得出第n个等腰三角形用了2×(n+1)+n根火柴棒,据此解答
【详解】第一个等腰三角形用了5=2×2+1根火柴棒,
第二个等腰三角形用了8=2×3+2根火柴棒,
第三个等腰三角形用了11=2×4+3根火柴棒,…
所以,第n个等腰三角形用了2×(n+1)+n=3n+2根火柴棒;
答:拼成n个这样的等腰三角形至少要(3n+2)根火柴棒。
【点睛】此题主要考查了图形的变化规律,注意结合图形发现蕴含的运算规律,找出解决问题的途径。
20.(2)14;17;(3)①29;② 3n+2
【分析】观察窗子上排列的方格图案,找到规律,从而进行推导得出答案。
【详解】(2)第一种有3×1+2=5个方格;
第二种有3×2+2=8个方格;
第三种有3×3+2=11个方格;
第n种则有(3n+2)个方格;
第四种则有3×4+2=14个方格;
第五种则有3×5+2=17个方格。
(3)①按照这样的规律排列,第9种窗子上使用了3×9+2=29个方格。
②按照这样的规律排列,第n种窗子上使用了(3n+2)个方格。
【点睛】本题考查图形的变化类为题,重点考查了学生通过观察、归纳、抽象出数的规律的能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
