思维拓展:多边形的面积图形计算-数学五年级上册苏教版(含解析)
文档属性
| 名称 | 思维拓展:多边形的面积图形计算-数学五年级上册苏教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
思维拓展:多边形的面积图形计算-数学五年级上册苏教版
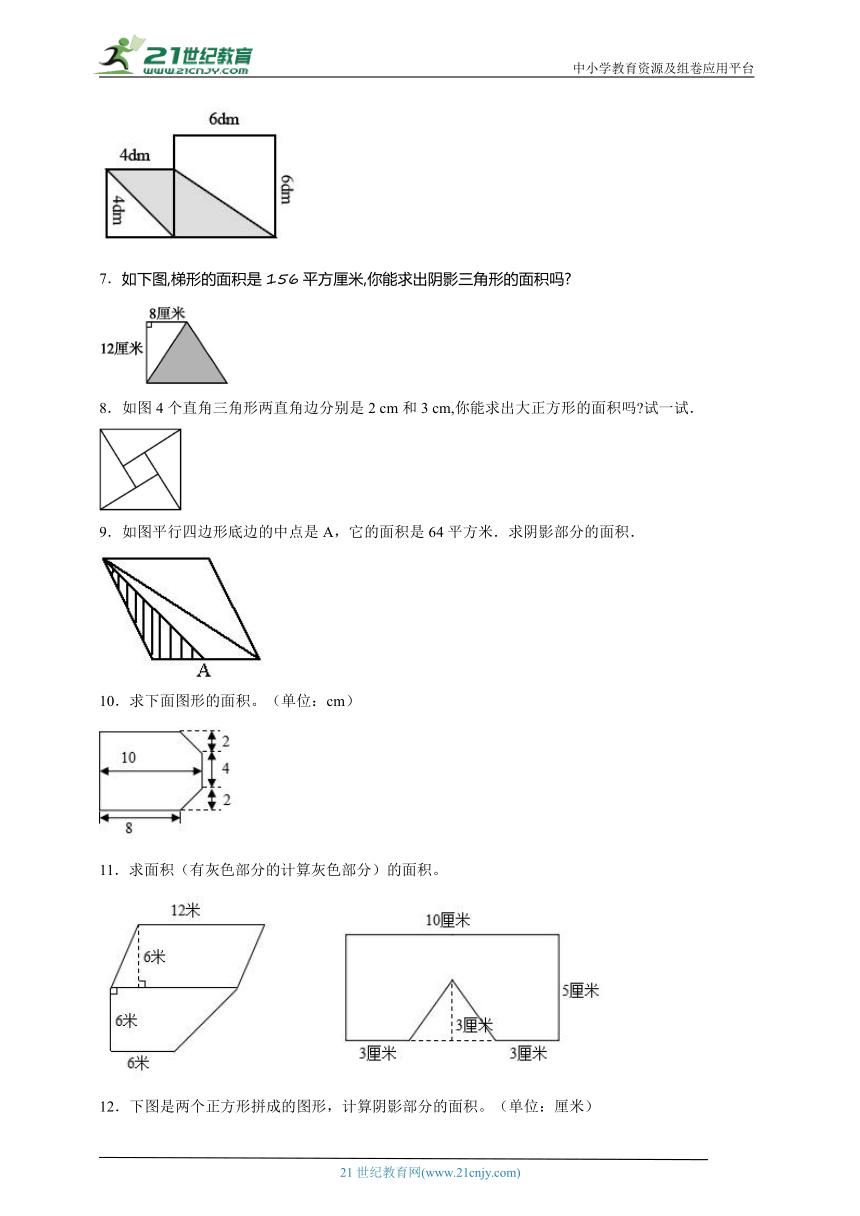
1.算一算下面阴影部分的面积。
2.求左图组合图形的面积,求右图阴影部分的面积。
3.求四边形ABCD的面积。(单位:厘米)
4.计算如图中阴影部分的面积。(单位:厘米)
5.如图,求阴影部分的面积之差。(单位:cm)
6.求阴影部分的面积。
7.如下图,梯形的面积是156平方厘米,你能求出阴影三角形的面积吗
8.如图4个直角三角形两直角边分别是2 cm和3 cm,你能求出大正方形的面积吗 试一试.
9.如图平行四边形底边的中点是A,它的面积是64平方米.求阴影部分的面积.
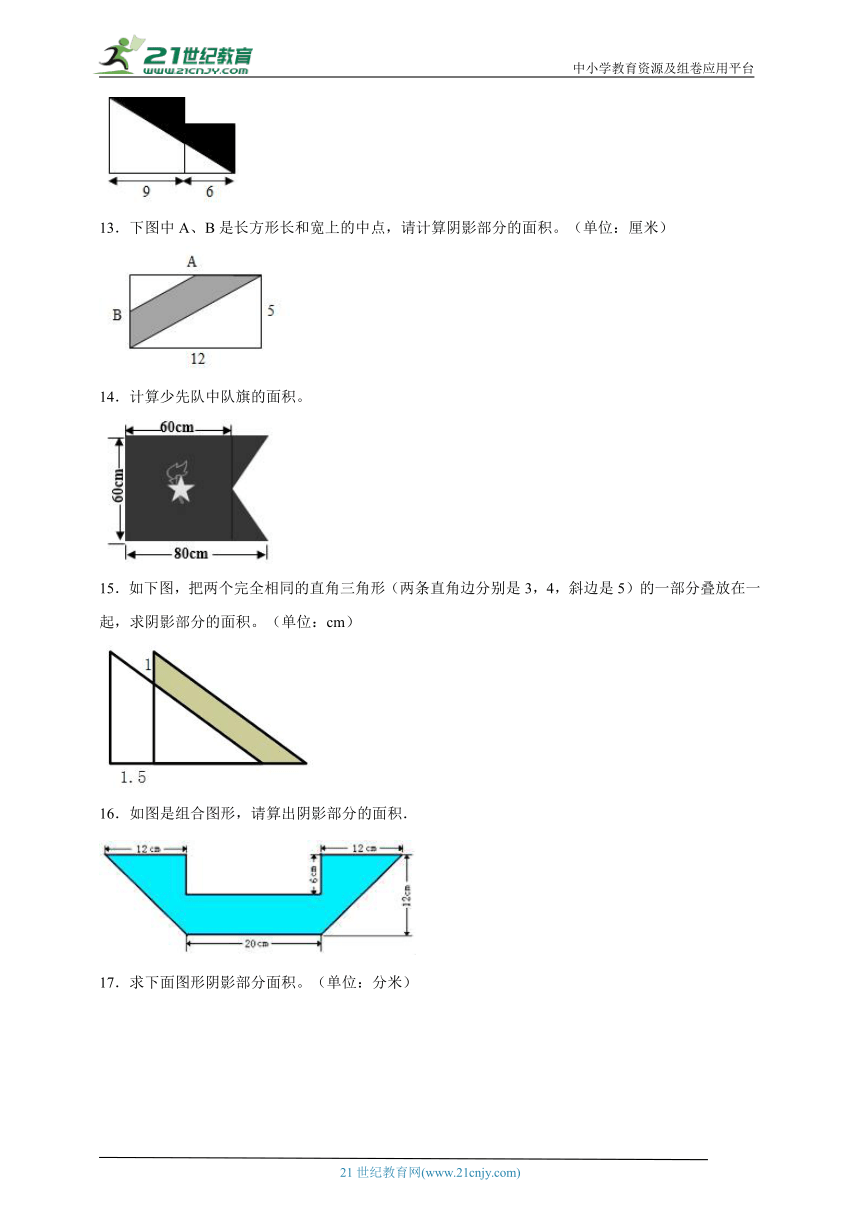
10.求下面图形的面积。(单位:cm)
11.求面积(有灰色部分的计算灰色部分)的面积。
12.下图是两个正方形拼成的图形,计算阴影部分的面积。(单位:厘米)
13.下图中A、B是长方形长和宽上的中点,请计算阴影部分的面积。(单位:厘米)
14.计算少先队中队旗的面积。
15.如下图,把两个完全相同的直角三角形(两条直角边分别是3,4,斜边是5)的一部分叠放在一起,求阴影部分的面积。(单位:cm)
16.如图是组合图形,请算出阴影部分的面积.
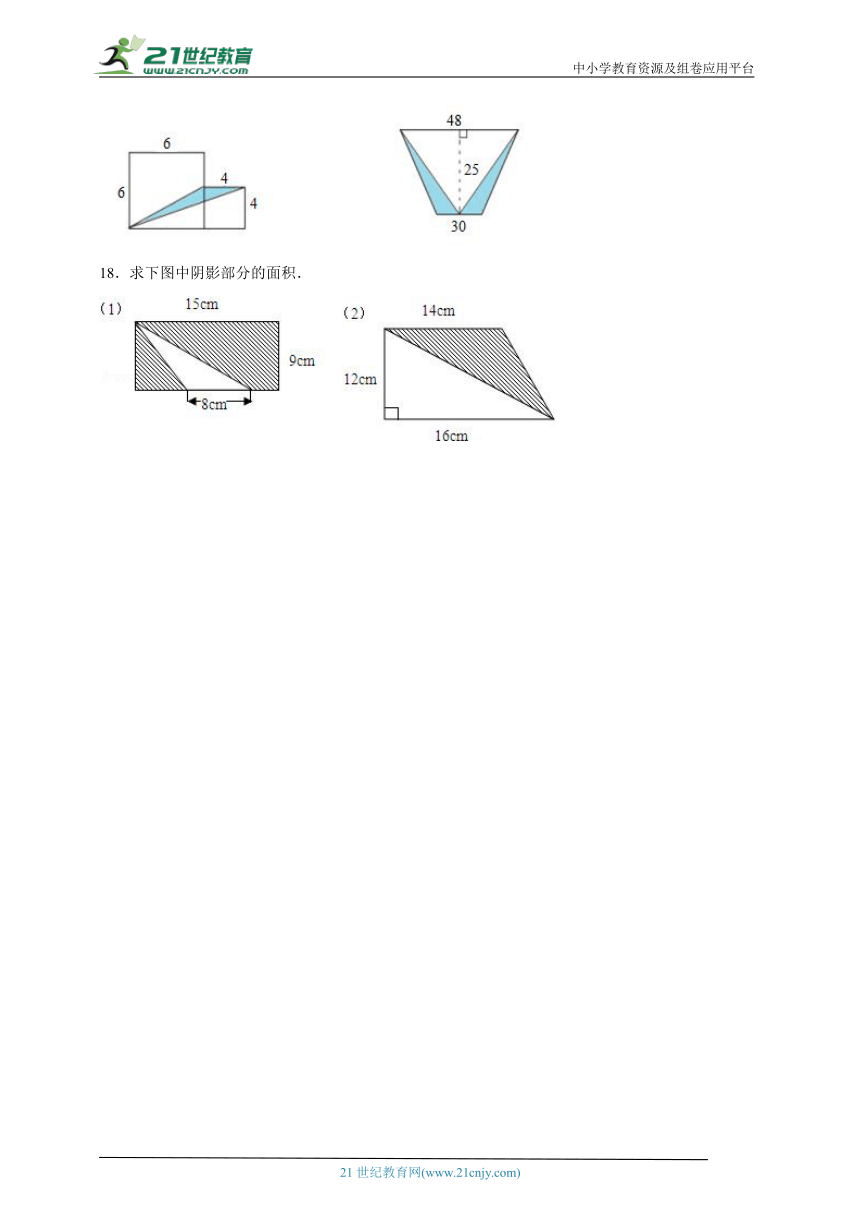
17.求下面图形阴影部分面积。(单位:分米)
18.求下图中阴影部分的面积.
参考答案:
1.20cm2
【分析】阴影部分是一个三角形,底为(11-6)cm,对应的高为8cm,代入三角形面积公式S=ah÷2计算即可。
【详解】(11-6)×8÷2
=5×8÷2
=40÷2
=20(cm2)
阴影部分的面积是20cm2。
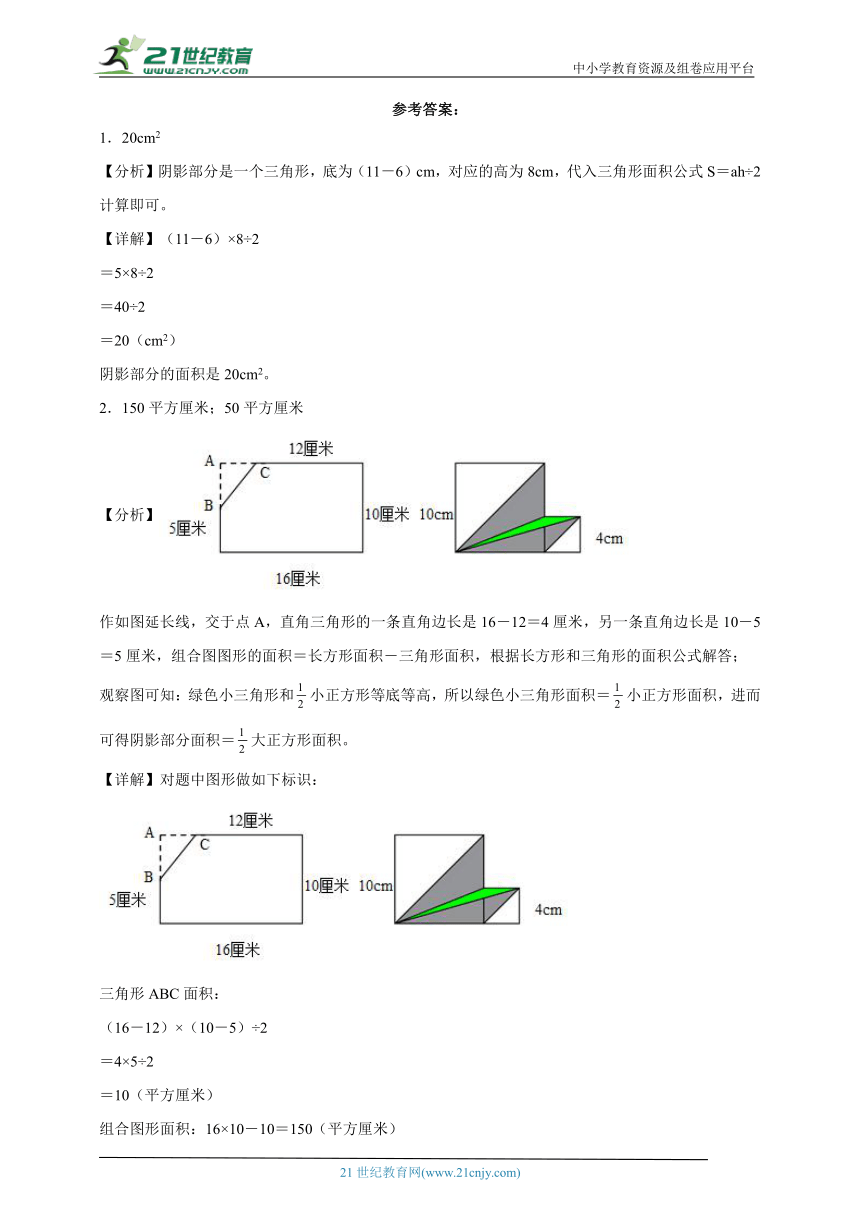
2.150平方厘米;50平方厘米
【分析】
作如图延长线,交于点A,直角三角形的一条直角边长是16-12=4厘米,另一条直角边长是10-5=5厘米,组合图图形的面积=长方形面积-三角形面积,根据长方形和三角形的面积公式解答;
观察图可知:绿色小三角形和小正方形等底等高,所以绿色小三角形面积=小正方形面积,进而可得阴影部分面积=大正方形面积。
【详解】对题中图形做如下标识:
三角形ABC面积:
(16-12)×(10-5)÷2
=4×5÷2
=10(平方厘米)
组合图形面积:16×10-10=150(平方厘米)
根据分析可知阴影部分的面积: 10×10÷2=50(平方厘米)
3.20平方厘米
【分析】如下图,延长BA、CD交于点E,则图形中就会出现两个等腰直角三角形,大等腰直角三角形的直角边长是7厘米、小等腰直角三角形的直角边长就是3厘米,则四边形ABCD的面积等于这两个三角形的面积之差,据此计算即可解答问题。
【详解】延长BA、CD交于点E,∠C=45°,则三角形EBC和三角形EAD是等腰直角三角形。
7×7÷2-3×3÷2
=24.5-4.5
=20(平方厘米)
4.9.5平方厘米
【分析】观察图可知:图中阴影部分的面积=大正方形面积+小正方形面积-大正方形面积的一半-直角三角形面积,根据正方形面积公式、三角形面积公式,将数值带入求值即可。
【详解】5×5+3×3﹣×5×5﹣×(5+3)×3
=25+9-12.5-×8×3
=21.5-12
=9.5(平方厘米)
5.12cm
【分析】求两个面积之差,如果不能直接求出,则加上公共部分得到两个可求的规则图形的面积之差。阴影部分面积之差=正方形ABCD的面积-三角形CEB的面积,据此解答。
【详解】(10+12)×12÷2
=22×12÷2
=22×6
=132(cm )
12×12=144(cm )
144-132=12(cm )
6.20dm2
【分析】图中阴影部分为梯形,其中梯形的上底为4dm,下底为6dm,高为4dm,梯形的面积公式=(上底+下底)×高÷2。将数据代入公式求解即可。
【详解】(4+6)×4÷2
=10×4÷2
=40÷2
=20(dm2)
7.(156×2÷12-8)×12÷2=108(cm2)
【详解】略
8.(3-2)×(3-2)+3×2÷2×4=13(cm2)
【详解】略
9.解:64÷4=16(平方米)
【详解】【分析】因A是平行四边形底边的中点,所以阴部分的面积和同它相邻的空白三角形的面积相等,它们等底等高,它们的和是平行四边形面积的一半,据此解答.
10.76cm2
【分析】观察图形,可分成两个上底是8cm,下底是10cm,高是2cm的梯形面积与一个长是10cm,宽是4cm的长方形面积的和;根据梯形面积公式:面积=(上底+下底)×高÷2,长方形面积公式:面积=长×高,代入数据,即可解答。
【详解】(8+10)×2÷2×2+10×4
=18×2÷2×2+40
=36÷2×2+40
=18×2+40
=36+40
=76(cm2)
11.126平方米;44平方厘米
【分析】(1)通过观察可知,图形是由一个平行四边形和梯形组成,根据平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,代数解答即可;
(2)通过观察可知,灰色部分面积=长方形面积-三角形面积,根据长方形面积=长×宽,三角形面积=底×高÷2,代数解答即可。
【详解】(1)12×6+(6+12)×6÷2
=72+54
=126(平方米)
(2)10×5-(10-3×2)×3÷2
=50-6
=44(平方厘米)
【点睛】此题主要考查学生对组合图形面积的认识与解答,将一个复杂图形转化为几个规则图形的组合是解题的关键。
12.49.5平方厘米
【分析】阴影部分的面积=两个正方形的面积之和-空白三角形的面积,据此解答。
【详解】9×9+6×6-(9+6)×9÷2
=81+36-67.5
=49.5(平方厘米)
13.22.5平方厘米
【分析】观察图形可知,阴影部分的面积=长方形的面积-两个空白三角形的面积,其中大空白三角形的底是12厘米,高是5厘米,小空白三角形的底是12÷2=6厘米,高是5÷2=2.5厘米,据此解答。
【详解】12÷2=6(厘米),5÷2=2.5(厘米)
12×5-12×5÷2-6×2.5÷2
=60-30-7.5
=22.5(平方厘米)
14.4200平方厘米
【分析】长方形的面积=80×60,空白三角形的面积=60×(80-60)÷2,长方形的面积-空白三角形的面积即为少先队中队旗的面积。
【详解】作图如下:
80×60-60×(80-60)÷2
=4800-600
=4200(平方厘米)
15.3.75平方厘米
【分析】图中是两个完全相同的直角三角形,所以除去重叠部分剩下的两个梯形的面积是相等的,梯形的面积=(上底+下底)×高÷2,已知空白梯形的上底是(3-1)厘米,下底是3厘米,高是1.5厘米,把数据代入公式计算即可。
【详解】(3-1+3)×1.5÷2
=5×1.5÷2
=3.75(cm )
所以阴影部分的面积是3.75平方厘米。
【点睛】找到阴影部分面积与空白梯形面积之间的关系是解题的关键,掌握梯形的面积公式。
16.264平方厘米
【详解】(20+12+20+12)×12÷2
=64×12÷2
=768÷2
=384(平方厘米)
20×6=120(平方厘米)
384﹣120=264(平方厘米)
答:阴影部分的面积是264平方厘米.
17.(1)8平方分米
(2)375平方分米
【详解】(1)4×4÷2=8(平方分米)
(2)30×25÷2=375(平方分米)
18.99平方厘米;84平方厘米.
【详解】试题分析:(1)阴影部分的面积用长方形的面积减去空白三角形的面积.
(2)阴影部分的面积就是底是14厘米,高是12厘米的三角形的面积,用三角形的面积公式计算即可.
解:(1)15×9﹣8×9÷2
=135﹣36
=99(平方厘米)
答:阴影部分的面积是99平方厘米.
(2)14×12÷2
=14×6
=84(平方厘米)
答:阴影部分的面积是84平方厘米.
【点评】本题考查了长方形面积公式长×宽=长方形的面积和三角形面积公式底×高÷2=三角形的面积的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:多边形的面积图形计算-数学五年级上册苏教版
1.算一算下面阴影部分的面积。
2.求左图组合图形的面积,求右图阴影部分的面积。
3.求四边形ABCD的面积。(单位:厘米)
4.计算如图中阴影部分的面积。(单位:厘米)
5.如图,求阴影部分的面积之差。(单位:cm)
6.求阴影部分的面积。
7.如下图,梯形的面积是156平方厘米,你能求出阴影三角形的面积吗
8.如图4个直角三角形两直角边分别是2 cm和3 cm,你能求出大正方形的面积吗 试一试.
9.如图平行四边形底边的中点是A,它的面积是64平方米.求阴影部分的面积.
10.求下面图形的面积。(单位:cm)
11.求面积(有灰色部分的计算灰色部分)的面积。
12.下图是两个正方形拼成的图形,计算阴影部分的面积。(单位:厘米)
13.下图中A、B是长方形长和宽上的中点,请计算阴影部分的面积。(单位:厘米)
14.计算少先队中队旗的面积。
15.如下图,把两个完全相同的直角三角形(两条直角边分别是3,4,斜边是5)的一部分叠放在一起,求阴影部分的面积。(单位:cm)
16.如图是组合图形,请算出阴影部分的面积.
17.求下面图形阴影部分面积。(单位:分米)
18.求下图中阴影部分的面积.
参考答案:
1.20cm2
【分析】阴影部分是一个三角形,底为(11-6)cm,对应的高为8cm,代入三角形面积公式S=ah÷2计算即可。
【详解】(11-6)×8÷2
=5×8÷2
=40÷2
=20(cm2)
阴影部分的面积是20cm2。
2.150平方厘米;50平方厘米
【分析】
作如图延长线,交于点A,直角三角形的一条直角边长是16-12=4厘米,另一条直角边长是10-5=5厘米,组合图图形的面积=长方形面积-三角形面积,根据长方形和三角形的面积公式解答;
观察图可知:绿色小三角形和小正方形等底等高,所以绿色小三角形面积=小正方形面积,进而可得阴影部分面积=大正方形面积。
【详解】对题中图形做如下标识:
三角形ABC面积:
(16-12)×(10-5)÷2
=4×5÷2
=10(平方厘米)
组合图形面积:16×10-10=150(平方厘米)
根据分析可知阴影部分的面积: 10×10÷2=50(平方厘米)
3.20平方厘米
【分析】如下图,延长BA、CD交于点E,则图形中就会出现两个等腰直角三角形,大等腰直角三角形的直角边长是7厘米、小等腰直角三角形的直角边长就是3厘米,则四边形ABCD的面积等于这两个三角形的面积之差,据此计算即可解答问题。
【详解】延长BA、CD交于点E,∠C=45°,则三角形EBC和三角形EAD是等腰直角三角形。
7×7÷2-3×3÷2
=24.5-4.5
=20(平方厘米)
4.9.5平方厘米
【分析】观察图可知:图中阴影部分的面积=大正方形面积+小正方形面积-大正方形面积的一半-直角三角形面积,根据正方形面积公式、三角形面积公式,将数值带入求值即可。
【详解】5×5+3×3﹣×5×5﹣×(5+3)×3
=25+9-12.5-×8×3
=21.5-12
=9.5(平方厘米)
5.12cm
【分析】求两个面积之差,如果不能直接求出,则加上公共部分得到两个可求的规则图形的面积之差。阴影部分面积之差=正方形ABCD的面积-三角形CEB的面积,据此解答。
【详解】(10+12)×12÷2
=22×12÷2
=22×6
=132(cm )
12×12=144(cm )
144-132=12(cm )
6.20dm2
【分析】图中阴影部分为梯形,其中梯形的上底为4dm,下底为6dm,高为4dm,梯形的面积公式=(上底+下底)×高÷2。将数据代入公式求解即可。
【详解】(4+6)×4÷2
=10×4÷2
=40÷2
=20(dm2)
7.(156×2÷12-8)×12÷2=108(cm2)
【详解】略
8.(3-2)×(3-2)+3×2÷2×4=13(cm2)
【详解】略
9.解:64÷4=16(平方米)
【详解】【分析】因A是平行四边形底边的中点,所以阴部分的面积和同它相邻的空白三角形的面积相等,它们等底等高,它们的和是平行四边形面积的一半,据此解答.
10.76cm2
【分析】观察图形,可分成两个上底是8cm,下底是10cm,高是2cm的梯形面积与一个长是10cm,宽是4cm的长方形面积的和;根据梯形面积公式:面积=(上底+下底)×高÷2,长方形面积公式:面积=长×高,代入数据,即可解答。
【详解】(8+10)×2÷2×2+10×4
=18×2÷2×2+40
=36÷2×2+40
=18×2+40
=36+40
=76(cm2)
11.126平方米;44平方厘米
【分析】(1)通过观察可知,图形是由一个平行四边形和梯形组成,根据平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,代数解答即可;
(2)通过观察可知,灰色部分面积=长方形面积-三角形面积,根据长方形面积=长×宽,三角形面积=底×高÷2,代数解答即可。
【详解】(1)12×6+(6+12)×6÷2
=72+54
=126(平方米)
(2)10×5-(10-3×2)×3÷2
=50-6
=44(平方厘米)
【点睛】此题主要考查学生对组合图形面积的认识与解答,将一个复杂图形转化为几个规则图形的组合是解题的关键。
12.49.5平方厘米
【分析】阴影部分的面积=两个正方形的面积之和-空白三角形的面积,据此解答。
【详解】9×9+6×6-(9+6)×9÷2
=81+36-67.5
=49.5(平方厘米)
13.22.5平方厘米
【分析】观察图形可知,阴影部分的面积=长方形的面积-两个空白三角形的面积,其中大空白三角形的底是12厘米,高是5厘米,小空白三角形的底是12÷2=6厘米,高是5÷2=2.5厘米,据此解答。
【详解】12÷2=6(厘米),5÷2=2.5(厘米)
12×5-12×5÷2-6×2.5÷2
=60-30-7.5
=22.5(平方厘米)
14.4200平方厘米
【分析】长方形的面积=80×60,空白三角形的面积=60×(80-60)÷2,长方形的面积-空白三角形的面积即为少先队中队旗的面积。
【详解】作图如下:
80×60-60×(80-60)÷2
=4800-600
=4200(平方厘米)
15.3.75平方厘米
【分析】图中是两个完全相同的直角三角形,所以除去重叠部分剩下的两个梯形的面积是相等的,梯形的面积=(上底+下底)×高÷2,已知空白梯形的上底是(3-1)厘米,下底是3厘米,高是1.5厘米,把数据代入公式计算即可。
【详解】(3-1+3)×1.5÷2
=5×1.5÷2
=3.75(cm )
所以阴影部分的面积是3.75平方厘米。
【点睛】找到阴影部分面积与空白梯形面积之间的关系是解题的关键,掌握梯形的面积公式。
16.264平方厘米
【详解】(20+12+20+12)×12÷2
=64×12÷2
=768÷2
=384(平方厘米)
20×6=120(平方厘米)
384﹣120=264(平方厘米)
答:阴影部分的面积是264平方厘米.
17.(1)8平方分米
(2)375平方分米
【详解】(1)4×4÷2=8(平方分米)
(2)30×25÷2=375(平方分米)
18.99平方厘米;84平方厘米.
【详解】试题分析:(1)阴影部分的面积用长方形的面积减去空白三角形的面积.
(2)阴影部分的面积就是底是14厘米,高是12厘米的三角形的面积,用三角形的面积公式计算即可.
解:(1)15×9﹣8×9÷2
=135﹣36
=99(平方厘米)
答:阴影部分的面积是99平方厘米.
(2)14×12÷2
=14×6
=84(平方厘米)
答:阴影部分的面积是84平方厘米.
【点评】本题考查了长方形面积公式长×宽=长方形的面积和三角形面积公式底×高÷2=三角形的面积的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
