思维拓展:多边形的面积综合-数学五年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展:多边形的面积综合-数学五年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 21:08:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
思维拓展:多边形的面积综合-数学五年级上册人教版
一、选择题
1.如图,把一张边长16cm的正方形纸片,沿虚线折叠,然后用剪刀将重叠部分剪去。那么被剪去部分的面积是( )平方厘米。
A.48 B.60 C.96 D.160
2.如图,在梯形中,涂色的两部分面积相比,甲( )乙。
A.小于 B.大于 C.等于
3.一个平行四边形和三角形的底相等,面积也相等,三角形的高是8厘米,平行四边形的高是( )。
A.8厘米 B.16厘米 C.4厘米
4.用65米的篱笆靠端墙围城一个梯形的养鸡场(如图),这个养鸡场占地面积是( )平方米。
A.1320 B.880 C.450 D.无法计算
5.一个梯形的下底是上底的1.5倍,高是18厘米,面积是540平方厘米,则这个梯形的上底是( )厘米。
A.24 B.4 C.36
6.一堆大小相同的圆木,堆成梯形形状,最下层有12根,最上层有6根,共堆了5层,这堆圆木共有( )。
A.51根 B.45根 C.66根 D.90根
二、填空题
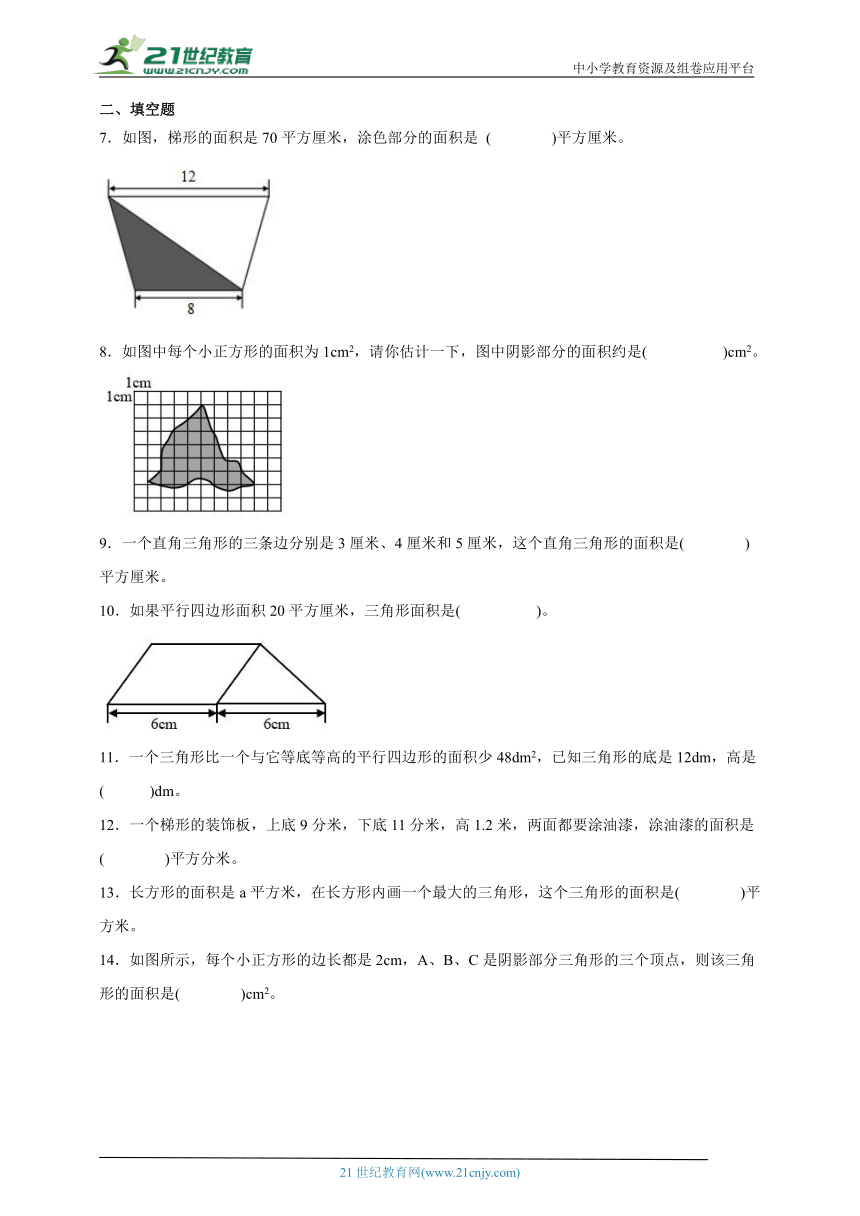
7.如图,梯形的面积是70平方厘米,涂色部分的面积是 ( )平方厘米。
8.如图中每个小正方形的面积为1cm2,请你估计一下,图中阴影部分的面积约是( )cm2。
9.一个直角三角形的三条边分别是3厘米、4厘米和5厘米,这个直角三角形的面积是( )平方厘米。
10.如果平行四边形面积20平方厘米,三角形面积是( )。
11.一个三角形比一个与它等底等高的平行四边形的面积少48dm2,已知三角形的底是12dm,高是( )dm。
12.一个梯形的装饰板,上底9分米,下底11分米,高1.2米,两面都要涂油漆,涂油漆的面积是( )平方分米。
13.长方形的面积是a平方米,在长方形内画一个最大的三角形,这个三角形的面积是( )平方米。
14.如图所示,每个小正方形的边长都是2cm,A、B、C是阴影部分三角形的三个顶点,则该三角形的面积是( )cm2。
三、图形计算
15.如下图,大正方形的边长是16厘米,求阴影部分的面积。
16.求阴影部分的面积。(单位:米)
四、解答题
17.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如下图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
18.学校后花园有一块梯形空地(如图),其中右边的平行四边形地里种花,剩下的阴影部分种草。种草的面积是多少平方米?
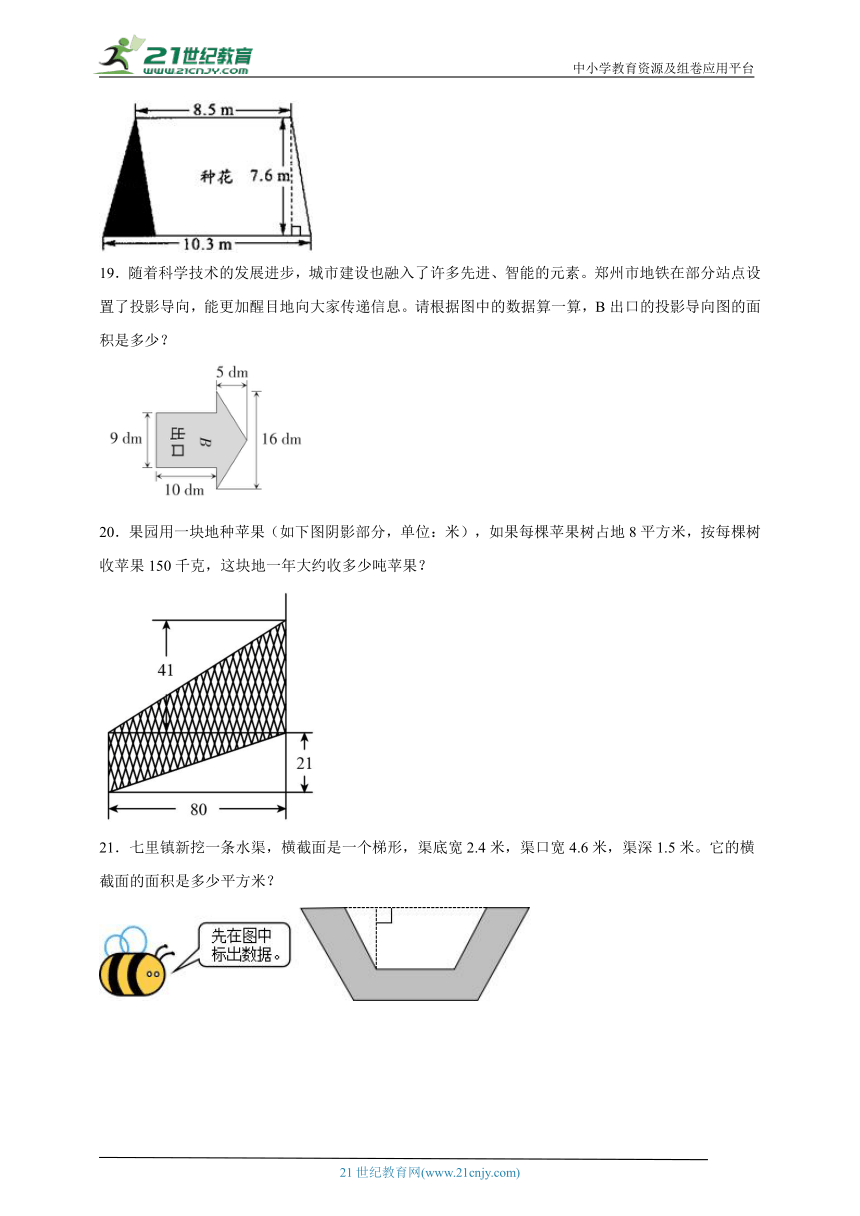
19.随着科学技术的发展进步,城市建设也融入了许多先进、智能的元素。郑州市地铁在部分站点设置了投影导向,能更加醒目地向大家传递信息。请根据图中的数据算一算,B出口的投影导向图的面积是多少?
20.果园用一块地种苹果(如下图阴影部分,单位:米),如果每棵苹果树占地8平方米,按每棵树收苹果150千克,这块地一年大约收多少吨苹果?
21.七里镇新挖一条水渠,横截面是一个梯形,渠底宽2.4米,渠口宽4.6米,渠深1.5米。它的横截面的面积是多少平方米?
参考答案:
1.A
【解析】由题意与图可知,被剪去的是一个直角三角形,它的底为(16-10)=6厘米;高为正方形的边长,再根据三角形的面积公式即可解答。
【详解】(16﹣10)×16÷2
=6×16÷2
=48(平方厘米),
答:被剪去部分的面积是48平方厘米。
故选:A。
【点睛】本题主要考查了图形的剪切以及三角形的面积,关键是要找出被剪去的三角形的底与高。
2.C
【分析】根据等底等高的三角形的面积相等,设图中空白部分小三角形的面积为丙,甲三角形的面积+丙三角形的面积=乙三角形的面积+丙三角形的面积,依此即可比较。
【详解】如图:根据题意可知,三角形ABD和三角形ABC等底等高,因此设图中空白部分小三角形的面积为丙,
甲三角形的面积+丙三角形的面积=乙三角形的面积+丙三角形的面积,因此甲、乙的面积相等。
故答案为:C
【点睛】此题考查的是等底等高的三角形的面积相等,应熟练掌握。
3.C
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2。用设数法,为了计算简便,可设平行四边形和三角形的底为1厘米。代入面积公式进行计算。
【详解】设平行四边形和三角形的底为1厘米。
三角形的面积:1×8÷2=4(平方厘米),平行四边形的高:4÷1=4(厘米)。
A.8厘米错误;
B.16厘米错误;
C.4厘米正确。
故答案为:C
【点睛】当平行四边形和三角形底相等,面积也相等时,三角形的高是平行四边形的高的2倍。
4.C
【分析】由图形可知,用篱笆的长度减去20米即可得到梯形的上底与下底的和,再根据梯形的面积公式:S=(a+b)×h÷2,据此进行计算即可。
【详解】(65-20)×20÷2
=45×20÷2
=900÷2
=450(平方米)
则这个养鸡场占地面积是450平方米。
故答案为:C
【点睛】本题考查梯形的面积,求出梯形的上底与下底的和是解题的关键。
5.A
【分析】根据梯形的面积=上下底之和×高÷2,可得梯形的上下底之和=梯形面积×2÷高,先求出梯形的上下底之和,再根据和倍公式求出上底即可。
【详解】540×2÷18
=1080÷18
=60(厘米),
60÷(1+1.5),
=60÷2.5,
=24(厘米),
梯形的上底是24厘米。
故选A。
【点睛】此题主要考查梯形的面积公式的灵活应用以及和倍公式的计算方法。
6.B
【分析】根据题意可知,圆木一共有5层,利用堆成梯形的物品的计算方法:根数=(上层根数+下层根数)×层数÷2,代入数据求出这堆圆木的根数,据此解答。
【详解】(12+6)×5÷2
=18×5÷2
=45(根)
这堆圆木共有45根。
故答案为:B
【点睛】本题的关键是根据堆成梯形物品的计算方法求出圆木的根数。
7.28
【分析】根据梯形的高=梯形的面积×2÷(上底+下底),用70×2÷(8+12)求出梯形的高,因为梯形的高等于阴影三角形的高,所以根据三角形的面积公式即可求出涂色部分面积。
【详解】70×2÷(8+12)
=140÷20
=7(厘米)
8×7÷2
=56÷2
=28(平方厘米)
涂色部分的面积是28平方厘米。
【点睛】本题考查了梯形面积公式和三角形面积公式的灵活应用。
8.24
【分析】先数完整的格子数量,再数不足一格的数量,不足一格的按半格计算,最后求和即可。
【详解】完整的格子有14个,不足一格的有20个,
14+20×0.5
=14+10
=24(cm2)
图中阴影部分的面积约是24cm2。
【点睛】掌握数格法求不规则图形的面积的方法是解题的关键。
9.6
【分析】由题意可知,一个直角三角形的三条边分别是3厘米、4厘米和5厘米,则这个三角形的底为3厘米,高为4厘米,根据三角形的面积公式:S=ah÷2,据此代入数值进行计算即可。
【详解】3×4÷2
=12÷2
=6(平方厘米)
则这个直角三角形的面积是6平方厘米。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
10.10平方厘米/10cm2
【分析】观察图形可知,图中三角形与平行四边形等底等高,根据“三角形的面积=底×高÷2、平行四边形的面积=底×高”可知:平行四边形的面积是与它等底等高的三角形的面积的2倍,据此可知:图中三角形与平行四边形等底等高,如果平行四边形面积20平方厘米,三角形面积是(20÷2)平方厘米。
【详解】20÷2=10(平方厘米)
所以,图中三角形与平行四边形等底等高,如果平行四边形面积20平方厘米,三角形面积是10平方厘米。
【点睛】明确平行四边形的面积和与它等底等高的三角形的面积的关系,是解题的关键。
11.8
【分析】因为等底等高的三角形的面积是平行四边形的面积的一半,又已知这个三角形比一个与它等底等高的平行四边形的面积少48dm2,所以三角形的面积是48dm2,由此根据三角形的面积公式S=ah÷2,得出h=2S÷a,代入数据求出三角形的高。
【详解】48×2÷12
=96÷12
=8(dm)
高是8dm。
【点睛】本题主要是利用等底等高的三角形的面积与平行四边形的面积的关系及三角形的面积公式解决问题。
12.240
【分析】根据梯形的面积公式:S=(a+b)h÷2,据此求出装饰板一面的面积,再用一面的面积乘2即可求出涂油漆的面积。
【详解】1.2米=12分米
(9+11)×12÷2×2
=20×12÷2×2
=240÷2×2
=120×2
=240(平方分米)
则涂油漆的面积是240平方分米。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
13.0.5a
【分析】在长方形内画一个最大的三角形,那么这个三角形的底等于长方形的长,高等于长方形的宽,根据三角形的面积=底×高÷2,长方形的面积=长×宽,可知这个三角形的面积等于长方形面积的一半,据此解答。
【详解】如图:
a÷2=0.5a(平方米)
这个三角形的面积是0.5a平方米。
【点睛】理解长方形和三角形的面积之间的关系,再用含字母的式子表示三角形的面积。
14.22
【分析】如图,三角形面积=大长方形面积-3个空白三角形的面积,长方形面积=长×宽,三角形面积=底×高÷2,据此列式计算。
【详解】4×2=8(cm)
3×2=6(cm)
2×2=4(cm)
1×2=2(cm)
8×6-6×2÷2-6×4÷2-8×2÷2
=48-6-12-8
=22(cm2)
该三角形的面积是22cm2。
【点睛】关键是掌握并灵活运用长方形和三角形面积公式。
15.128平方厘米
【分析】假设出小正方形的边长,整个图形的面积=梯形ABCF的面积+正方形CDEF的面积,空白部分的面积=三角形ABD的面积+三角形DEF的面积,阴影部分的面积=整个图形的面积-空白部分的面积,据此解答。
【详解】假设小正方形的边长为a厘米。
(a+16)×a÷2+16×16-(a+16)×a÷2-16×16÷2
=(a+16)×a÷2-(a+16)×a÷2+16×16-16×16÷2
=(a2+16a)÷2-(a2+16a)÷2+16×16-16×16÷2
=16×16-16×16÷2
=256-256÷2
=256-128
=128(平方厘米)
所以,阴影部分的面积是128平方厘米。
16.27平方米
【分析】通过观察发现:阴影部分为梯形,上底是3米,下底是6米,高是6米。根据梯形的面积=(上底+下底)×高÷2可求出阴影部分的面积。
【详解】(3+6)×6÷2
=9×6÷2
=54÷2
=27(平方米)
17.21平方米
【分析】这块地的形状是梯形,梯形的上底是(3.6+2.6)米,梯形的下底是(2.2+2.6+3)米,梯形的高是3米。梯形的面积=(上底+下底)×高÷2,把梯形上底、下底、高的数值代入公式计算即可求出这块地的面积。
【详解】上底:3.6+2.6=6.2(米)
下底:2.2+2.6+3
=4.8+3
=7.8(米)
面积:(6.2+7.8)×3÷2
=14×3÷2
=42÷2
=21(平方米)
答:这块地的面积共有21平方米。
【点睛】此题主要考查了梯形面积计算公式的应用。计算梯形的面积时,不要忘记除以2。
18.6.84平方米
【分析】种草的阴影部分是三角形。将梯形的下底减去上底,求出三角形的底。三角形的高和梯形的高相等。据此,再根据三角形面积=底×高÷2,求出种草部分的面积。
【详解】(10.3-8.5)×7.6÷2
=1.8×7.6÷2
=6.84(平方米)
答:种草的面积是6.84平方米。
【点睛】本题考查了三角形的面积,熟记三角形的面积公式是解题的关键。
19.130平方分米
【分析】看图可知,投影导向图可以分成一个长方形加上一个三角形,根据长方形的面积公式:长×宽;三角形的面积公式:(底×高)÷2,两者面积加起来即可求出投影导向图的面积。
【详解】长方形的面积:10×9=90(平方分米)
三角形的面积:16×5÷2
=80÷2
=40(平方分米)
90+40=130(平方分米)
答:B出口的投影导向图的面积是130平方分米。
【点睛】此题考查了学生对三角形的面积公式以及长方形的面积公式的熟练掌握程度。
20.46.5吨
【分析】观察图形可知,阴影部分是一个上底为21米、下底为41米、高为80米的梯形,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出这块地的面积。
已知每棵苹果树占地8平方米,用这块地的面积除以每棵苹果树的占地面积,即可求出苹果树的棵数;再乘每棵苹果树收苹果的质量,求出这块地收苹果的总质量;最后根据进率“1吨=1000千克”换算单位即可。
【详解】这块地的面积:
(21+41)×80÷2
=62×80÷2
=2480(平方米)
苹果的总棵数:2480÷8=310(棵)
苹果的总质量:150×310=46500(千克)
46500千克=46.5吨
答:这块地一年大约收46.5吨苹果。
【点睛】本题考查梯形面积公式的运用以及质量单位的换算,也可以把阴影部分分成两个三角形,分别求出面积再相加,即是这块地的面积。
21.5.25平方米
【分析】根据题意,水渠的横截面是一个梯形,先在图中标出梯形的上底、下底和高,然后根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个水渠横截面的面积。
【详解】如图:
(2.4+4.6)×1.5÷2
=7×1.5÷2
=10.5÷2
=5.25(平方米)
答:它的横截面的面积是5.25平方米。
【点睛】本题考查梯形各部分的认识以及梯形面积公式的运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:多边形的面积综合-数学五年级上册人教版
一、选择题
1.如图,把一张边长16cm的正方形纸片,沿虚线折叠,然后用剪刀将重叠部分剪去。那么被剪去部分的面积是( )平方厘米。
A.48 B.60 C.96 D.160
2.如图,在梯形中,涂色的两部分面积相比,甲( )乙。
A.小于 B.大于 C.等于
3.一个平行四边形和三角形的底相等,面积也相等,三角形的高是8厘米,平行四边形的高是( )。
A.8厘米 B.16厘米 C.4厘米
4.用65米的篱笆靠端墙围城一个梯形的养鸡场(如图),这个养鸡场占地面积是( )平方米。
A.1320 B.880 C.450 D.无法计算
5.一个梯形的下底是上底的1.5倍,高是18厘米,面积是540平方厘米,则这个梯形的上底是( )厘米。
A.24 B.4 C.36
6.一堆大小相同的圆木,堆成梯形形状,最下层有12根,最上层有6根,共堆了5层,这堆圆木共有( )。
A.51根 B.45根 C.66根 D.90根
二、填空题
7.如图,梯形的面积是70平方厘米,涂色部分的面积是 ( )平方厘米。
8.如图中每个小正方形的面积为1cm2,请你估计一下,图中阴影部分的面积约是( )cm2。
9.一个直角三角形的三条边分别是3厘米、4厘米和5厘米,这个直角三角形的面积是( )平方厘米。
10.如果平行四边形面积20平方厘米,三角形面积是( )。
11.一个三角形比一个与它等底等高的平行四边形的面积少48dm2,已知三角形的底是12dm,高是( )dm。
12.一个梯形的装饰板,上底9分米,下底11分米,高1.2米,两面都要涂油漆,涂油漆的面积是( )平方分米。
13.长方形的面积是a平方米,在长方形内画一个最大的三角形,这个三角形的面积是( )平方米。
14.如图所示,每个小正方形的边长都是2cm,A、B、C是阴影部分三角形的三个顶点,则该三角形的面积是( )cm2。
三、图形计算
15.如下图,大正方形的边长是16厘米,求阴影部分的面积。
16.求阴影部分的面积。(单位:米)
四、解答题
17.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如下图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
18.学校后花园有一块梯形空地(如图),其中右边的平行四边形地里种花,剩下的阴影部分种草。种草的面积是多少平方米?
19.随着科学技术的发展进步,城市建设也融入了许多先进、智能的元素。郑州市地铁在部分站点设置了投影导向,能更加醒目地向大家传递信息。请根据图中的数据算一算,B出口的投影导向图的面积是多少?
20.果园用一块地种苹果(如下图阴影部分,单位:米),如果每棵苹果树占地8平方米,按每棵树收苹果150千克,这块地一年大约收多少吨苹果?
21.七里镇新挖一条水渠,横截面是一个梯形,渠底宽2.4米,渠口宽4.6米,渠深1.5米。它的横截面的面积是多少平方米?
参考答案:
1.A
【解析】由题意与图可知,被剪去的是一个直角三角形,它的底为(16-10)=6厘米;高为正方形的边长,再根据三角形的面积公式即可解答。
【详解】(16﹣10)×16÷2
=6×16÷2
=48(平方厘米),
答:被剪去部分的面积是48平方厘米。
故选:A。
【点睛】本题主要考查了图形的剪切以及三角形的面积,关键是要找出被剪去的三角形的底与高。
2.C
【分析】根据等底等高的三角形的面积相等,设图中空白部分小三角形的面积为丙,甲三角形的面积+丙三角形的面积=乙三角形的面积+丙三角形的面积,依此即可比较。
【详解】如图:根据题意可知,三角形ABD和三角形ABC等底等高,因此设图中空白部分小三角形的面积为丙,
甲三角形的面积+丙三角形的面积=乙三角形的面积+丙三角形的面积,因此甲、乙的面积相等。
故答案为:C
【点睛】此题考查的是等底等高的三角形的面积相等,应熟练掌握。
3.C
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2。用设数法,为了计算简便,可设平行四边形和三角形的底为1厘米。代入面积公式进行计算。
【详解】设平行四边形和三角形的底为1厘米。
三角形的面积:1×8÷2=4(平方厘米),平行四边形的高:4÷1=4(厘米)。
A.8厘米错误;
B.16厘米错误;
C.4厘米正确。
故答案为:C
【点睛】当平行四边形和三角形底相等,面积也相等时,三角形的高是平行四边形的高的2倍。
4.C
【分析】由图形可知,用篱笆的长度减去20米即可得到梯形的上底与下底的和,再根据梯形的面积公式:S=(a+b)×h÷2,据此进行计算即可。
【详解】(65-20)×20÷2
=45×20÷2
=900÷2
=450(平方米)
则这个养鸡场占地面积是450平方米。
故答案为:C
【点睛】本题考查梯形的面积,求出梯形的上底与下底的和是解题的关键。
5.A
【分析】根据梯形的面积=上下底之和×高÷2,可得梯形的上下底之和=梯形面积×2÷高,先求出梯形的上下底之和,再根据和倍公式求出上底即可。
【详解】540×2÷18
=1080÷18
=60(厘米),
60÷(1+1.5),
=60÷2.5,
=24(厘米),
梯形的上底是24厘米。
故选A。
【点睛】此题主要考查梯形的面积公式的灵活应用以及和倍公式的计算方法。
6.B
【分析】根据题意可知,圆木一共有5层,利用堆成梯形的物品的计算方法:根数=(上层根数+下层根数)×层数÷2,代入数据求出这堆圆木的根数,据此解答。
【详解】(12+6)×5÷2
=18×5÷2
=45(根)
这堆圆木共有45根。
故答案为:B
【点睛】本题的关键是根据堆成梯形物品的计算方法求出圆木的根数。
7.28
【分析】根据梯形的高=梯形的面积×2÷(上底+下底),用70×2÷(8+12)求出梯形的高,因为梯形的高等于阴影三角形的高,所以根据三角形的面积公式即可求出涂色部分面积。
【详解】70×2÷(8+12)
=140÷20
=7(厘米)
8×7÷2
=56÷2
=28(平方厘米)
涂色部分的面积是28平方厘米。
【点睛】本题考查了梯形面积公式和三角形面积公式的灵活应用。
8.24
【分析】先数完整的格子数量,再数不足一格的数量,不足一格的按半格计算,最后求和即可。
【详解】完整的格子有14个,不足一格的有20个,
14+20×0.5
=14+10
=24(cm2)
图中阴影部分的面积约是24cm2。
【点睛】掌握数格法求不规则图形的面积的方法是解题的关键。
9.6
【分析】由题意可知,一个直角三角形的三条边分别是3厘米、4厘米和5厘米,则这个三角形的底为3厘米,高为4厘米,根据三角形的面积公式:S=ah÷2,据此代入数值进行计算即可。
【详解】3×4÷2
=12÷2
=6(平方厘米)
则这个直角三角形的面积是6平方厘米。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
10.10平方厘米/10cm2
【分析】观察图形可知,图中三角形与平行四边形等底等高,根据“三角形的面积=底×高÷2、平行四边形的面积=底×高”可知:平行四边形的面积是与它等底等高的三角形的面积的2倍,据此可知:图中三角形与平行四边形等底等高,如果平行四边形面积20平方厘米,三角形面积是(20÷2)平方厘米。
【详解】20÷2=10(平方厘米)
所以,图中三角形与平行四边形等底等高,如果平行四边形面积20平方厘米,三角形面积是10平方厘米。
【点睛】明确平行四边形的面积和与它等底等高的三角形的面积的关系,是解题的关键。
11.8
【分析】因为等底等高的三角形的面积是平行四边形的面积的一半,又已知这个三角形比一个与它等底等高的平行四边形的面积少48dm2,所以三角形的面积是48dm2,由此根据三角形的面积公式S=ah÷2,得出h=2S÷a,代入数据求出三角形的高。
【详解】48×2÷12
=96÷12
=8(dm)
高是8dm。
【点睛】本题主要是利用等底等高的三角形的面积与平行四边形的面积的关系及三角形的面积公式解决问题。
12.240
【分析】根据梯形的面积公式:S=(a+b)h÷2,据此求出装饰板一面的面积,再用一面的面积乘2即可求出涂油漆的面积。
【详解】1.2米=12分米
(9+11)×12÷2×2
=20×12÷2×2
=240÷2×2
=120×2
=240(平方分米)
则涂油漆的面积是240平方分米。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
13.0.5a
【分析】在长方形内画一个最大的三角形,那么这个三角形的底等于长方形的长,高等于长方形的宽,根据三角形的面积=底×高÷2,长方形的面积=长×宽,可知这个三角形的面积等于长方形面积的一半,据此解答。
【详解】如图:
a÷2=0.5a(平方米)
这个三角形的面积是0.5a平方米。
【点睛】理解长方形和三角形的面积之间的关系,再用含字母的式子表示三角形的面积。
14.22
【分析】如图,三角形面积=大长方形面积-3个空白三角形的面积,长方形面积=长×宽,三角形面积=底×高÷2,据此列式计算。
【详解】4×2=8(cm)
3×2=6(cm)
2×2=4(cm)
1×2=2(cm)
8×6-6×2÷2-6×4÷2-8×2÷2
=48-6-12-8
=22(cm2)
该三角形的面积是22cm2。
【点睛】关键是掌握并灵活运用长方形和三角形面积公式。
15.128平方厘米
【分析】假设出小正方形的边长,整个图形的面积=梯形ABCF的面积+正方形CDEF的面积,空白部分的面积=三角形ABD的面积+三角形DEF的面积,阴影部分的面积=整个图形的面积-空白部分的面积,据此解答。
【详解】假设小正方形的边长为a厘米。
(a+16)×a÷2+16×16-(a+16)×a÷2-16×16÷2
=(a+16)×a÷2-(a+16)×a÷2+16×16-16×16÷2
=(a2+16a)÷2-(a2+16a)÷2+16×16-16×16÷2
=16×16-16×16÷2
=256-256÷2
=256-128
=128(平方厘米)
所以,阴影部分的面积是128平方厘米。
16.27平方米
【分析】通过观察发现:阴影部分为梯形,上底是3米,下底是6米,高是6米。根据梯形的面积=(上底+下底)×高÷2可求出阴影部分的面积。
【详解】(3+6)×6÷2
=9×6÷2
=54÷2
=27(平方米)
17.21平方米
【分析】这块地的形状是梯形,梯形的上底是(3.6+2.6)米,梯形的下底是(2.2+2.6+3)米,梯形的高是3米。梯形的面积=(上底+下底)×高÷2,把梯形上底、下底、高的数值代入公式计算即可求出这块地的面积。
【详解】上底:3.6+2.6=6.2(米)
下底:2.2+2.6+3
=4.8+3
=7.8(米)
面积:(6.2+7.8)×3÷2
=14×3÷2
=42÷2
=21(平方米)
答:这块地的面积共有21平方米。
【点睛】此题主要考查了梯形面积计算公式的应用。计算梯形的面积时,不要忘记除以2。
18.6.84平方米
【分析】种草的阴影部分是三角形。将梯形的下底减去上底,求出三角形的底。三角形的高和梯形的高相等。据此,再根据三角形面积=底×高÷2,求出种草部分的面积。
【详解】(10.3-8.5)×7.6÷2
=1.8×7.6÷2
=6.84(平方米)
答:种草的面积是6.84平方米。
【点睛】本题考查了三角形的面积,熟记三角形的面积公式是解题的关键。
19.130平方分米
【分析】看图可知,投影导向图可以分成一个长方形加上一个三角形,根据长方形的面积公式:长×宽;三角形的面积公式:(底×高)÷2,两者面积加起来即可求出投影导向图的面积。
【详解】长方形的面积:10×9=90(平方分米)
三角形的面积:16×5÷2
=80÷2
=40(平方分米)
90+40=130(平方分米)
答:B出口的投影导向图的面积是130平方分米。
【点睛】此题考查了学生对三角形的面积公式以及长方形的面积公式的熟练掌握程度。
20.46.5吨
【分析】观察图形可知,阴影部分是一个上底为21米、下底为41米、高为80米的梯形,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出这块地的面积。
已知每棵苹果树占地8平方米,用这块地的面积除以每棵苹果树的占地面积,即可求出苹果树的棵数;再乘每棵苹果树收苹果的质量,求出这块地收苹果的总质量;最后根据进率“1吨=1000千克”换算单位即可。
【详解】这块地的面积:
(21+41)×80÷2
=62×80÷2
=2480(平方米)
苹果的总棵数:2480÷8=310(棵)
苹果的总质量:150×310=46500(千克)
46500千克=46.5吨
答:这块地一年大约收46.5吨苹果。
【点睛】本题考查梯形面积公式的运用以及质量单位的换算,也可以把阴影部分分成两个三角形,分别求出面积再相加,即是这块地的面积。
21.5.25平方米
【分析】根据题意,水渠的横截面是一个梯形,先在图中标出梯形的上底、下底和高,然后根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个水渠横截面的面积。
【详解】如图:
(2.4+4.6)×1.5÷2
=7×1.5÷2
=10.5÷2
=5.25(平方米)
答:它的横截面的面积是5.25平方米。
【点睛】本题考查梯形各部分的认识以及梯形面积公式的运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
