数学人教A版(2019)必修第一册3.2.1函数的单调性(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.1函数的单调性(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
3.2.1函数的单调性
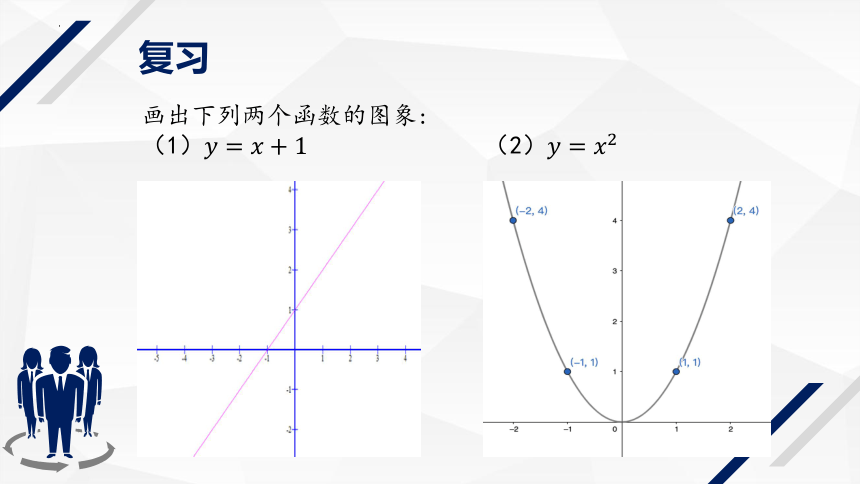
复习
画出下列两个函数的图象:
(1)(2)
提出问题,导入新课
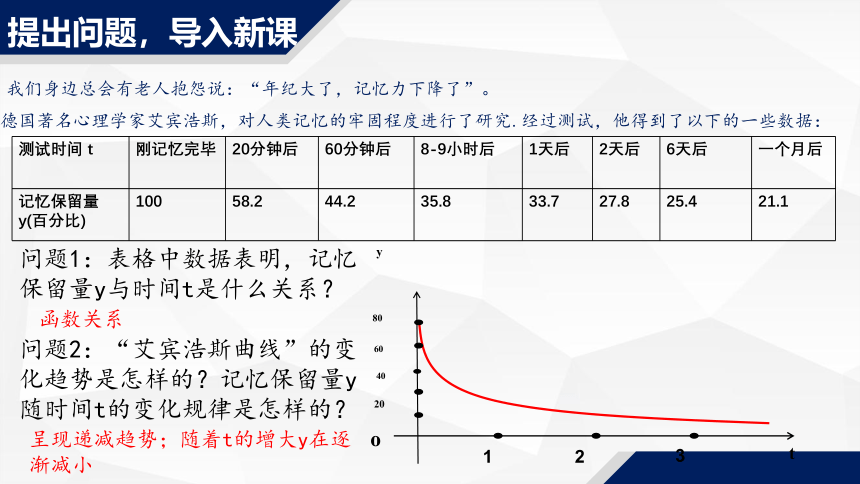
我们身边总会有老人抱怨说:“年纪大了,记忆力下降了”。
德国著名心理学家艾宾浩斯,对人类记忆的牢固程度进行了研究.经过测试,他得到了以下的一些数据:
测试时间 t 刚记忆完毕 20分钟后 60分钟后 8-9小时后 1天后 2天后 6天后 一个月后
记忆保留量y(百分比) 100 58.2 44.2 35.8 33.7 27.8 25.4 21.1
t
y
o
20
40
60
80
1
2
3
问题1:表格中数据表明,记忆保留量y与时间t是什么关系?
问题2:“艾宾浩斯曲线”的变化趋势是怎样的?记忆保留量y随时间t的变化规律是怎样的?
函数关系
呈现递减趋势;随着t的增大y在逐渐减小
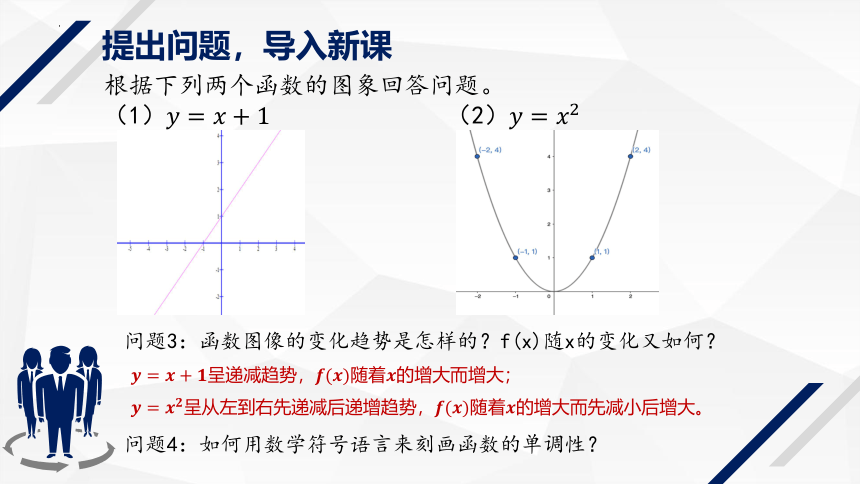
根据下列两个函数的图象回答问题。
(1)(2)
提出问题,导入新课
问题3:函数图像的变化趋势是怎样的?f(x)随x的变化又如何?
问题4:如何用数学符号语言来刻画函数的单调性?
提出问题,导入新课
(1)研究函数要明确什么?
定义域
(2)对于一个函数例如
不唯一
(3)利用数学语言如何描述
对于任意的
一般的,设函数f(x)的定义域为D,
区间I D;
如果任意∈I,若,则,那么就称函数f(x) 在区间I上单调递增
提出问题,导入新课
思考辨析1:若在区间(0,+ ∞)上取自变量1,2,∵1<2, 则f(1)任意∈(0,+ ∞ )
取特殊值无法在代表集合中取任意元素
提出问题,导入新课
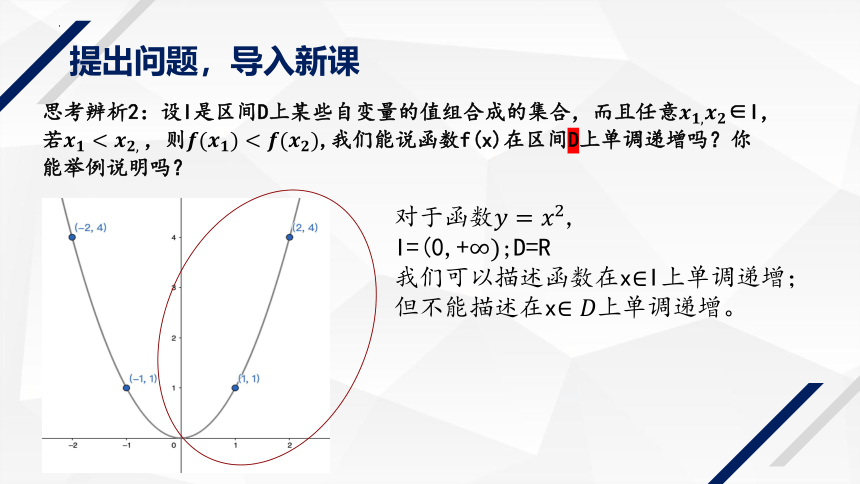
思考辨析2:设I是区间D上某些自变量的值组合成的集合,而且任意∈I,若,则,我们能说函数f(x)在区间D上单调递增吗?你能举例说明吗?
对于函数,
I=(0,+;D=R
我们可以描述函数在xI上单调递增;但不能描述在x上单调递增。
提出问题,导入新课
问题5:你能否类比单调增函数的研究方法来定义单调减函数
一般的,设函数f(x)的定义域为D,
区间I D;
如果任意∈I,若,则 ,那么就称函数f(x) 在区间I上单调递增
一般的,设函数f(x)的定义域为D,
区间I D;
如果任意∈I,若,则,那么就称函数f(x) 在区间I上单调递减
师生互动,探索新知
知识点1:函数的单调性
不等号方向相同
不等号方向相反
提出问题,导入新课
知识点2.函数的单调性及单调区间
(1)当函数在它的定义域上单调递增(减)时,我们就称它是增(减)函数(单调函数).
例如:
(2)如果函数在区间I上单调递增或单调递减,那么就说函数在这一区间具有(严格的)单调性,区间I叫做的单调区间.
例如:对于函数,I=(0,+;I为y=f(x)的单调递增区间
停顿
学以致用,巩固新知
例1-1:下列命题为真命题的是( ).
A.定义在 上的函数 ,如果 ,当有 时,有 ,那么在 上单调递增
B.如果函数 在区间 上单调递减,在区间 上也单调递减,那么在区间 上就一定单调递减
C.定义在 上的函数,若有无穷多对 ,当 时,有 ,那么 在 上为增函数
D. ,当 , 成立,则函数 在 上不是单增
D
学以致用,巩固新知
例1-2:如图,分别为函数 的图像,试分别写出 的单调递增区间
答案:图(1)函数
停顿
例1-3. 如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调增区间和单调减区间?
学以致用,巩固新知
答案:如图所示,函数在[-2,1]和[3,5] 上,是单调递增的,所以的单调递增区间是[-2,1]和[3,5] .
如图所示,函数在[-5,-2)和(1,3)上,是单调递减的,f(x)的单调递减区间是[-5,-2)和(1,3).
思考辨析:
此时能否说函数y=f(x),
在区间[-2,1)∪(3,5]上单调递增?
学以致用,巩固新知
v
例1-4:
(1)根据图像写出两个函数的单调区间,以及在单调区间上的函数是增函数还是减函数.
答案:图(1)的单调区间为 ,且在此区间上是增函数.
图(2)的单调区间为 ,且在此区间上是减函数
学以致用,巩固新知
v
例1-4:
(2)根据定义,
研究函数的单调 性。
证明:
即,
②当k=0时,
即,
③当k0
即,
则函数在定义域R上单调递增。
则函数在定义域R上无单调性。
则函数在定义域R上单调递减。
课堂练习:
1.判断正误
(1)函数f(x)= 在 R上是单调增函数; ( )
(2)定义在R上的函数f(x)满足f(2)>f(1),则函数 f (x) 在R上是增函数;( )
(3)所有函数在定义域上都具有单调性;( )
(4)若f(x)为R上的减函数,则f(0)>f(1);( )
(5)若函数f(x)在区间(1,2]和(2,3)上均为增函数,则函数f(x)在区间(1,3)上为增函数. ( )
课堂练习:
2.根据定义,
(1)证明函数的单调性;
证明:
,
,
,
则有;函数在定义域R上单调递减。
课堂练习:
2.根据定义,
(2)证明函数的单调性.
证明:
,
则在区间(0,;
,则在区间(;
区间[0,;
在区间(.
复习总结:
1.单调性两个定义:
一般的,设函数f(x)的定义域为D,区间ID;
如果任意∈I,若,则f(,
那么就称函数f(x) 在区间I上单调递增;
如果任意∈I,若,则f(,
那么就称函数f(x) 在区间I上单调递减.
复习总结:
2.判断单调性的两种方法:
①定义法(注意:要证明单调性,在单调区间内取值要确保任意性,不能取特殊值)
②图像法(明确画出函数图像)
复习总结:
3.单调函数,单调区间,函数的单调性区分:
函数的单调性:也叫函数的增减性,可以定性描述在一个指定区间内,函数值(因变量)变化与自变量变化的关系。当函数f(x) 的自变量在其定义区间内增大(或减小)时,函数值也随着增大(或减小),则称该函数为在该区间上具有单调性(单调递增或单调递减) 。
注意:函数单调性是针对某一个区间而言的,是一个局部性质。因此,说单调性时最好指明区间。有些函数在整个定义域内是单调的;有些函数在定义域内的部分区间上是增函数,在部分区间上是减函数;有些函数是非单调函数,如常数函数(y=1)。函数的单调性是函数在一个单调区间上的“整体”性质,具有任意性,不能用特殊值代替。
复习总结:
3.单调函数,单调区间,函数的单调性区分:
单调区间:如果一个函数具有相同单调性的单调区间不止一个,那么这些单调区间不能用“∪”(并,或)连接,而只能用“逗号”或“和”字隔开。
复习总结:
3.单调函数,单调区间,函数的单调性区分:
单调函数: 一般地,设一连续函数 f(x) 的定义域为D,则如果对于属于定义域D内的任意两个自变量∈D,若,则,即在D上具有唯一单调性且单调递增,那么就说f(x) 在定义域是单调增函数。相反地,如果对于定义域D内任意∈D,若,则,即在定义域D上具有单调性且单调递减,那么就说 f(x) 在定义域上是单调减函数。则增函数和减函数统称单调函数。
注意:对于单调函数单调区间只有一个就是函数的定义域,并且在整个定义域内函数的单调性唯一且连续。(反比例函数就不是单调函数)
课后作业
1.完成79页课后练习题第1、2、3、4题;
2.预习思考如何利用函数的单调性找到函数的最值。
感谢你这么好看,
还那么认真的倾听!
停顿
3.2.1函数的单调性
复习
画出下列两个函数的图象:
(1)(2)
提出问题,导入新课
我们身边总会有老人抱怨说:“年纪大了,记忆力下降了”。
德国著名心理学家艾宾浩斯,对人类记忆的牢固程度进行了研究.经过测试,他得到了以下的一些数据:
测试时间 t 刚记忆完毕 20分钟后 60分钟后 8-9小时后 1天后 2天后 6天后 一个月后
记忆保留量y(百分比) 100 58.2 44.2 35.8 33.7 27.8 25.4 21.1
t
y
o
20
40
60
80
1
2
3
问题1:表格中数据表明,记忆保留量y与时间t是什么关系?
问题2:“艾宾浩斯曲线”的变化趋势是怎样的?记忆保留量y随时间t的变化规律是怎样的?
函数关系
呈现递减趋势;随着t的增大y在逐渐减小
根据下列两个函数的图象回答问题。
(1)(2)
提出问题,导入新课
问题3:函数图像的变化趋势是怎样的?f(x)随x的变化又如何?
问题4:如何用数学符号语言来刻画函数的单调性?
提出问题,导入新课
(1)研究函数要明确什么?
定义域
(2)对于一个函数例如
不唯一
(3)利用数学语言如何描述
对于任意的
一般的,设函数f(x)的定义域为D,
区间I D;
如果任意∈I,若,则,那么就称函数f(x) 在区间I上单调递增
提出问题,导入新课
思考辨析1:若在区间(0,+ ∞)上取自变量1,2,∵1<2, 则f(1)
取特殊值无法在代表集合中取任意元素
提出问题,导入新课
思考辨析2:设I是区间D上某些自变量的值组合成的集合,而且任意∈I,若,则,我们能说函数f(x)在区间D上单调递增吗?你能举例说明吗?
对于函数,
I=(0,+;D=R
我们可以描述函数在xI上单调递增;但不能描述在x上单调递增。
提出问题,导入新课
问题5:你能否类比单调增函数的研究方法来定义单调减函数
一般的,设函数f(x)的定义域为D,
区间I D;
如果任意∈I,若,则 ,那么就称函数f(x) 在区间I上单调递增
一般的,设函数f(x)的定义域为D,
区间I D;
如果任意∈I,若,则,那么就称函数f(x) 在区间I上单调递减
师生互动,探索新知
知识点1:函数的单调性
不等号方向相同
不等号方向相反
提出问题,导入新课
知识点2.函数的单调性及单调区间
(1)当函数在它的定义域上单调递增(减)时,我们就称它是增(减)函数(单调函数).
例如:
(2)如果函数在区间I上单调递增或单调递减,那么就说函数在这一区间具有(严格的)单调性,区间I叫做的单调区间.
例如:对于函数,I=(0,+;I为y=f(x)的单调递增区间
停顿
学以致用,巩固新知
例1-1:下列命题为真命题的是( ).
A.定义在 上的函数 ,如果 ,当有 时,有 ,那么在 上单调递增
B.如果函数 在区间 上单调递减,在区间 上也单调递减,那么在区间 上就一定单调递减
C.定义在 上的函数,若有无穷多对 ,当 时,有 ,那么 在 上为增函数
D. ,当 , 成立,则函数 在 上不是单增
D
学以致用,巩固新知
例1-2:如图,分别为函数 的图像,试分别写出 的单调递增区间
答案:图(1)函数
停顿
例1-3. 如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调增区间和单调减区间?
学以致用,巩固新知
答案:如图所示,函数在[-2,1]和[3,5] 上,是单调递增的,所以的单调递增区间是[-2,1]和[3,5] .
如图所示,函数在[-5,-2)和(1,3)上,是单调递减的,f(x)的单调递减区间是[-5,-2)和(1,3).
思考辨析:
此时能否说函数y=f(x),
在区间[-2,1)∪(3,5]上单调递增?
学以致用,巩固新知
v
例1-4:
(1)根据图像写出两个函数的单调区间,以及在单调区间上的函数是增函数还是减函数.
答案:图(1)的单调区间为 ,且在此区间上是增函数.
图(2)的单调区间为 ,且在此区间上是减函数
学以致用,巩固新知
v
例1-4:
(2)根据定义,
研究函数的单调 性。
证明:
即,
②当k=0时,
即,
③当k0
即,
则函数在定义域R上单调递增。
则函数在定义域R上无单调性。
则函数在定义域R上单调递减。
课堂练习:
1.判断正误
(1)函数f(x)= 在 R上是单调增函数; ( )
(2)定义在R上的函数f(x)满足f(2)>f(1),则函数 f (x) 在R上是增函数;( )
(3)所有函数在定义域上都具有单调性;( )
(4)若f(x)为R上的减函数,则f(0)>f(1);( )
(5)若函数f(x)在区间(1,2]和(2,3)上均为增函数,则函数f(x)在区间(1,3)上为增函数. ( )
课堂练习:
2.根据定义,
(1)证明函数的单调性;
证明:
,
,
,
则有;函数在定义域R上单调递减。
课堂练习:
2.根据定义,
(2)证明函数的单调性.
证明:
,
则在区间(0,;
,则在区间(;
区间[0,;
在区间(.
复习总结:
1.单调性两个定义:
一般的,设函数f(x)的定义域为D,区间ID;
如果任意∈I,若,则f(,
那么就称函数f(x) 在区间I上单调递增;
如果任意∈I,若,则f(,
那么就称函数f(x) 在区间I上单调递减.
复习总结:
2.判断单调性的两种方法:
①定义法(注意:要证明单调性,在单调区间内取值要确保任意性,不能取特殊值)
②图像法(明确画出函数图像)
复习总结:
3.单调函数,单调区间,函数的单调性区分:
函数的单调性:也叫函数的增减性,可以定性描述在一个指定区间内,函数值(因变量)变化与自变量变化的关系。当函数f(x) 的自变量在其定义区间内增大(或减小)时,函数值也随着增大(或减小),则称该函数为在该区间上具有单调性(单调递增或单调递减) 。
注意:函数单调性是针对某一个区间而言的,是一个局部性质。因此,说单调性时最好指明区间。有些函数在整个定义域内是单调的;有些函数在定义域内的部分区间上是增函数,在部分区间上是减函数;有些函数是非单调函数,如常数函数(y=1)。函数的单调性是函数在一个单调区间上的“整体”性质,具有任意性,不能用特殊值代替。
复习总结:
3.单调函数,单调区间,函数的单调性区分:
单调区间:如果一个函数具有相同单调性的单调区间不止一个,那么这些单调区间不能用“∪”(并,或)连接,而只能用“逗号”或“和”字隔开。
复习总结:
3.单调函数,单调区间,函数的单调性区分:
单调函数: 一般地,设一连续函数 f(x) 的定义域为D,则如果对于属于定义域D内的任意两个自变量∈D,若,则,即在D上具有唯一单调性且单调递增,那么就说f(x) 在定义域是单调增函数。相反地,如果对于定义域D内任意∈D,若,则,即在定义域D上具有单调性且单调递减,那么就说 f(x) 在定义域上是单调减函数。则增函数和减函数统称单调函数。
注意:对于单调函数单调区间只有一个就是函数的定义域,并且在整个定义域内函数的单调性唯一且连续。(反比例函数就不是单调函数)
课后作业
1.完成79页课后练习题第1、2、3、4题;
2.预习思考如何利用函数的单调性找到函数的最值。
感谢你这么好看,
还那么认真的倾听!
停顿
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
