专题06勾股定理 期中专题复习(含解析)2023年秋苏科版数学八年级上册
文档属性
| 名称 | 专题06勾股定理 期中专题复习(含解析)2023年秋苏科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览

文档简介
专题06 勾股定理
勾股定理——面积问题
(2022·宿迁期中)
1.如图,、、分别是以的三边为直径所画半圆的面积,其中,,则 .
(2022·连云港期中)
2.如图,在四边形中,,分别以四边形的四条边为边长,向外作四个正方形,面积分别为,,和.若,,,则的值是 .
(2022·扬州期中)
3.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、6、20,则正方形B的面积为) .
(2022·镇江期中)
4.如图,在中,,分别以、、为边向上作正方形,已知的面积为,则图中阴影部分面积之和为 .
勾股定理——距离问题
(2022·南京期中)
5.如图,在中,,,,则点A到的距离是( )
A.10 B.11 C.12 D.13
(2022·南通期中)
6.如图,网格中的每个小正方形的边长为1,的顶点A、B、C均在网格的格点上,于点D,则BD的长为( )
A. B. C. D.
(2022·无锡期中)
7.如图,,已知中,,,的顶点A、B分别在边、上,当点B在边上运动时,点A随之在边上运动,的形状保持不变,在运动过程中,点C到点O的最大距离为( )
A.5 B.6 C.7 D.8
8.如图,,动点A和C分别在射线OP、OQ上运动,且,作,且.在运动过程中,OB的最大距离是( )
A.5cm B. C. D.3cm
勾股定理——折叠问题
(2022·常州期中)
9.如图,在矩形ABCD中,,.点E是边BC上一点,沿AE翻折,点B恰好落在CD边上点F处,则CE的长是( )
A. B. C. D.3
(2022·盐城期中)
10.如图,把四边形EDFB纸片分别沿AB和DC折叠,恰好使得点E和点D、点F和点B重合,在折叠成的新四边形ABCD中,,,则的面积是 .
勾股定理——特殊三角形的存在性问题2
(2022·苏州期中)
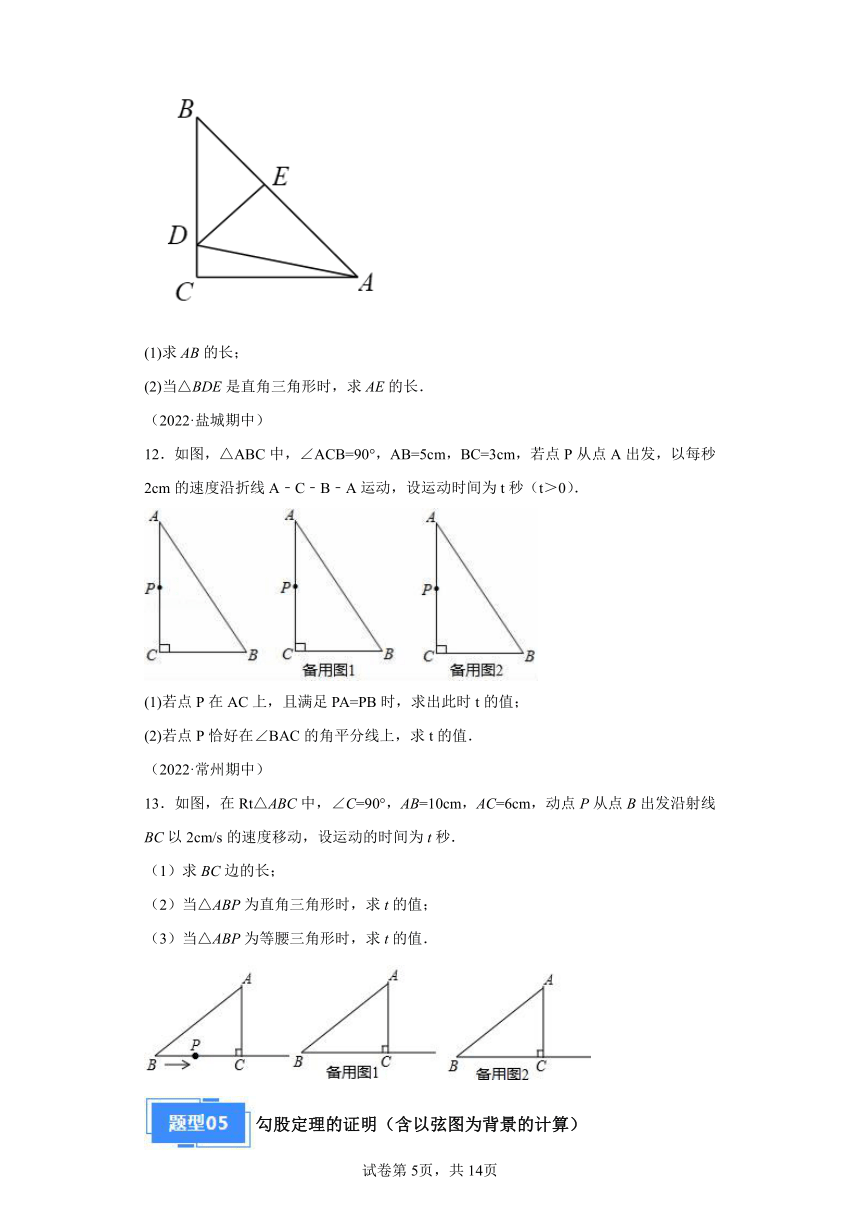
11.如图,在△ABC中,,D为BC边上一点,且,,,点E是AB边上的动点,连接DE.
(1)求AB的长;
(2)当△BDE是直角三角形时,求AE的长.
(2022·盐城期中)
12.如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
(2022·常州期中)
13.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
勾股定理的证明(含以弦图为背景的计算)
(2022·苏州期中)
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
(2022·无锡期中)
15.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为81,小正方形面积为16,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( )
A.x2+y2=81 B.x+y=13 C.2xy+16=81 D.x-y=4
(2022·常州期中)
16.(1)图1是由有20个边长为1的正方形组成的,把它按图1的分割方法分割成5部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图2的网格中画出拼接成的大正方形.
(2)如果(1)中分割成的直角三角形两直角边分别为a,b斜边为c.请你利用图2中拼成的大正方形证明勾股定理.
(3)应用:测量旗杆的高度:校园内有一旗杆,小希想知道旗杆的高度,经观察发现从顶端垂下一根拉绳,于是他测出了下列数据:①测得拉绳垂到地面后,多出的长度为0.5米;②他在距离旗杆4米的地方拉直绳子,拉绳的下端恰好距离地面0.5米.请你根据所测得的数据设计可行性方案,解决这一问题.(画出示意图并计算出这根旗杆的高度).
(2022·扬州期中)
17.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为),也可以表示为,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路,且.测得千米,千米,求新路比原路少多少千米?
(3)在第(2)问中若时,,,,,设,求x的值.
勾股数
(2022·苏州期中)
18.以下数组中,其中是勾股数的是( )
A. , , B.9 ,40 , 41
C.1 , ,1 D.2 ,3 ,4
(2022·连云港期中)
19.如果正整数a、b、c满足等式,那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )
A.47 B.62 C.79 D.98
(2022·南通期中)
20.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即,那么称m为广义勾股数.则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( )
A.②④ B.①②④ C.①② D.①④
(2022·扬州期中)
21.同学们都知道,凡是可以构成一个直角三角形三边的一组正整数,称之为“勾股数”.比如3,4,5或11,60,61等.
(1)请你写出另外两组勾股数:6,_____,_____;7,_____,_____;
(2)清朝的扬州籍数学家罗士琳提出了四个构造勾股数的法则,其中有两个法则如下:
(Ⅰ)如果是大于1的奇数,那么,,是一组勾股数
(Ⅱ)如果是大于2的偶数,那么,,是一组勾股数
①如果在一组勾股数中,其中有一个数为12,根据法则(Ⅰ)求出另外两个数;
②请证明两个法则的正确性.
勾股定理的逆定理——直角三角形的判定
(2022·泰州期中·改编)
22.下列各组线段能构成直角三角形的一组是( )
A.,, B.,,
C.,, D.,,
(2022·常州期中)
23.如图,在由单位正方形组成的网格图中标有四条线段,其中能构成一个直角三角形三边的线段是( )
A. B. C. D.
(2022·无锡/盐城期中)
24.以下四组代数式作为△ABC的三边,能使△ABC为直角三角形的有:①3n,4n,5n,(n为正整数);②n,n+1,n+2(n为正整数);③n2-1,2n,n2+1(n≥2,n为正整数);④m2-n2,2mn,m2+n2(m>n,m,n为正整数) ( )
A.1组 B.2组 C.3组 D.4组
(2022·泰州期中)
25.如图,,垂足为D,且,.点E从B点沿射线向右以2个单位/秒的速度匀速运动,F为的中点,连接,设点E运动的时间为t.
(1)当t为何值时,;
(2)当时,判断的形状,并说明理由.
勾股定理的逆定理——直角三角形的判定与性质
(2022·常州期中)
26.如图,在中,,,,为边上一动点,于,于,则的取值范围为( )
A. B. C. D.
(2022·无锡期中)
27.如图所示的是正方形网格,则∠MDC﹣∠MAB= °(点A,B,C,D,M.网格线交点).
(2022·常州期中)
28.如图,正方形网格中每一个小正方形的边长为1,小正方形的顶点为格点,点,,为格点,点为与网格线的交点,则 .
(2022·镇江期中)
29.如图,已知在中,,,,为边上一个动点,连接,,分别交、于点、,垂足为,点为的中点,若四边形的面积为18,则的最大值为 .
(2022·宿迁期中)
30.图,四边形中,,,,,,求四边形的面积.
(2022·南京期中)
31.如图,在中,边上的垂直平分线与分别交于点和,且.
(1)求证:;
(2)若,,求的长.
勾股定理的实际应用
32.如图,一圆柱高,底面半径为,一只蚂蚁从点爬到点处吃食,要爬行的最短路程(取3)是( )
A. B. C. D.无法确定
(2022·南京/无锡/常州/南通期中)
33.在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何 它的意思是:一根竹子原高一丈(尺),中部一处折断,竹梢触地面处离竹根尺,试问折断处离地面 尺.
(2022·常州/苏州/淮安期中)
34.将一根24cm的筷子置于底面直径为8cm,高为15cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是 .
(2022·南通期中)
35.如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km,B村庄到公路的距离BD=14km,测得C、D两点的距离为20km,现要在CD之间建一个服务区E,使得A、B两村庄到E服务区的距离相等,求CE的长.
(2022·盐城期中)
36.一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
(2022·淮安期中)
37.森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点, 且点 C与直线 AB上两点A,B的距离分别为600m和800m,又AB=1000m,飞机中心周围500m 以内可以受到洒水影响.
(1)着火点C受洒水影响吗?为什么?
(2)若飞机的速度为10 m/s,要想扑灭着火点C估计需要13秒,请你通过计算判断着火点C能否被扑灭?
(2022·苏州期中)
38.如图,在弦图中,正方形的对角线与正方形的对角线交于点K,对角线交正方形于G,J两点,记面积为,面积为,若,则的值为 .
(2022·南通期中)
39.如图△ABC中,∠ACB=90°,AC=12,BC=5.若动点P从点C开始以每秒1个单位的速度,按C→A→B的路径运动,设运动的时间为t秒,当t为 时,△BCP为等腰三角形.
(2022·无锡期中)
40.如图,已知在中,,D是上的一点,,点P从B点出发沿射线方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连接.
(1)当秒时,求的长度(结果保留根号);
(2)当为等腰三角形时,求t的值;
(3)过点D作于点E.在点P的运动过程中,当t为何值时,能使?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.
【分析】先分别算出、、的面积,然后根据勾股定理即可解答.
【详解】解:∵,,
∴
∵
∴.
∵,,
∴
故答案为.
【点睛】本题主要考查了勾股定理的应用,勾股定理的内容是直角三角形的两条直角边的平方和等于斜边的平方.
2.8
【分析】连接AC,构造和,然后在中利用勾股定理求出,在中求出,进而求得的值.
【详解】解:如图所示,连接,
在中,,
即;
同理,在中,,
即,
则.
故答案为:8.
【点睛】本题考查勾股定理,解决本题的关键是将面积转化为勾股定理求边长平方即可.
3.10
【分析】根据勾股定理的几何意义:解得即可.
【详解】解:如图,
由题意:,
∵正方形A、C、D的面积依次为4、6、20,
∴,
∴.
故答案为:10.
【点睛】本题考查了勾股定理,要熟悉勾股定理的几何意义,知道直角三角形两直角边的平方和等于斜边的平方.
4.
【分析】利用勾股定理和正方形的面积公式可得,利用正方形的性质证明和,根据全等三角形的面积相等,从而得出,,再根据三个正方形面积的关系可得出,从而可得阴影面积之和.
【详解】解:如图,设,,,
∵在中,,
∴,
∵四边形,四边形和四边形都是正方形,
∴,,,
∴,
∵四边形和四边形是正方形,
∴,,,
∴是直角三角形,
在和中,
,
∴
∴,
∵四边形和四边形是正方形,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∵,
又∵,
,
,
∴,
∴,
∴图中阴影部分面积之和为.
故答案为:.
【点睛】本题考查正方形的性质,勾股定理,全等三角形的判定和性质,等角的余角相等等知识,运用了等积变换的思想方法.运用等积变换是解题的关键.
5.C
【分析】过点作交的延长线于点,根据勾股定理求得,进而勾股定理求得,即可求解.
【详解】解:如图,过点作交的延长线于点,
∴,
∵,,,
∴
∴
解得:,
∴,
即点A到的距离是.
故选:C.
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
6.C
【分析】通过面积相等法求解即可.
【详解】解:如图所示:
,
∵,
即,
解得:.
故选:C.
【点睛】本题考查网格内求面积,想到是关键.
7.C
【分析】由先等腰三角形的性质得,由勾股定理求出,再由三角形的三边关系得,则当O、D、C共线时,OC有最大值,最大值是,然后由直角三角形斜边上的中线性质求出,即可解决问题.
【详解】解:取的中点D,连接,如图所示:
∵,,
∵点D是AB边中点,
∴,
∴,
连接OD,OC,有,
当共线时,有最大值,最大值是,
又∵为直角三角形,D为斜边的中点,
∴,
∴,
即点C到点O的最大距离为7,
故选:C.
【点睛】此题考查的是勾股定理,等腰三角形的性质,直角三角形斜边上的中线性质以及三角形的三边关系等知识,证出OC最大时的长为CD+OD是解本题的关键.
8.B
【分析】取AC中点D,连接BD,OD,根据数形结合分析可知,根据B,O,D的位置关系求OB的最大距离.
【详解】解:取AC中点D,连接BD,OD,
∵,D为AC中点,
∴,,
在中,,
∴,
由图像可知,
当B,O,D三点共线时,等号成立,
∴OB的最大距离是.
故选:B.
【点睛】本题考查了动点和定点距离的最大值和直角三角形斜边的中线等于斜边的一半,解决本题的关键是分析B,O,D的位置关系.
9.B
【分析】根据折叠的性质可知,AF=AB=10,根据勾股定理求出DF,进而求出CF;在根据勾股定理即可得,列出等式求解即可.
【详解】∵△AFE由△ABE沿AE翻折得到;
∴△AFE≌△ABE,
∴AF=AB=10,EF=BE
在Rt△ADF中,由勾股定理可得:,
∵四边形ABCD为矩形,
∴CD=AB=10,
∴CF=CD-DF=10-8=2,
设CE=x,则BE=EF=6-x,
在Rt△CEF中,由勾股定理可得:,
解得:x=,
故选:B
【点睛】本题主要考查了勾股定理、折叠的性质以及矩形的性质,熟练地掌握矩形的性质和折叠的性质,根据勾股定理列出等式是解题的关键.
10.
【分析】先由勾股定理求出BD,DC的长,过点F作FHED交ED的延长线于H,再证,得到FH=AD=3,由SBEF=S四边形BEDF-SEDF即可得到答案.
【详解】解:∵ABD是由ABE折叠而成,BDC是由FDC折叠而成,
∴BE=BD,EA=AD,BC=FC,BD=DF,
∴BAED, DCBF,BE=BD=DF,,
∵AD=3,AB=4,BC=,
∴BD=,
∴,
∴BCD=DBC=45
∴ BDF=90,
如图,过点F作FHED交ED的延长线于H,
∵ABD+ADB=90,FDH+ADB=90,
∴ABD=FDH,
∴在ABD和HDF中,
∴,
∴FH=AD=3,
∴SBEF=S四边形BEDF-SEDF= SEBD+SDBF- SEDF
=.
【点睛】此题主要考查了勾股定理,轴对称的性质,全等三角形的判定与性质及三角形的面积,正确的添加辅助线证明三角形全等是解决问题的关键.
11.(1)
(2)AE的长为或3
【分析】(1)先根据勾股定理证明△ACD是直角三角形,且,求得,然后根据勾股定理直接计算即可求解.
(2)根据等边对等角以及直角三角形的两锐角互余可得,根据△BDE是直角三角形需分两种情况分析:①当时,,②当时,根据勾股定以及等面积法即可求解.
【详解】(1)解:在△ACD中,∵,,,
∴,
∴△ACD是直角三角形,且,
∵,
∴,
∴在Rt△ACB中,;
(2)∵,,
∴,
∴△BDE是直角三角形需分两种情况分析:
①当时,,
∴在Rt△BDE中,,
∴;
②当时,,即,
解得:,
∴,
∴;
综上所述,AE的长为或3.
【点睛】本题考查了勾股定理与勾股定理的逆定理,等腰三角形的性质,掌握勾股定理是解题的关键.
12.(1)t=;(2)t=;
【分析】(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4-2t,根据勾股定理列方程即可得到结论;
(2)当点P在∠CAB的平分线上时,如图,过点P作PE⊥AB于点E,此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,根据勾股定理列方程即可得到结论.
【详解】(1)设存在点P,使得PA=PB,此时PA=PB=2t,
在Rt△ABC中,AC===4,PC=4–2t,
在Rt△PCB中,PC2+CB2=PB2,即:(4–2t)2+32=(2t)2,
解得t=,
∴当t=时,PA=PB;
(2)当点P在∠BAC的平分线上时,如图,过点P作PE⊥AB于点E,
此时BP=7–2t,PE=PC=2t–4,BE=5–4=1,
在Rt△BEP中,PE2+BE2=BP2,
即:(2t–4)2+12=(7–2t)2,解得t=,
∴当t=时,P在∠BAC的平分线上.
【点睛】本题考查的是三角形的综合运用,熟练掌握勾股定理是解题的关键.
13.(1)8cm;(2)4或;(3)5或8或.
【分析】(1)直接根据勾股定理求出BC的长度;
(2)当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
(3)当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP时,分别求出BP的长度,继而可求得t值.
【详解】解:(1)在Rt△ABC中,BC2=AB2 AC2=102 62=64,
∴BC=8(cm);
(2)由题意知BP=2tcm,
①当∠APB为直角时,点P与点C重合,BP=BC=8cm,即t=4;
②当∠BAP为直角时,BP=2tcm,CP=(2t 8)cm,AC=6cm,
在Rt△ACP中,AP2=62+(2t 8)2,
在Rt△BAP中,AB2+AP2=BP2,
即:102+[62+(2t 8)2]=(2t)2,
解得:t=,
故当△ABP为直角三角形时,t=4或t=;
(3)①当AB=BP时,t=5;
②当AB=AP时,BP=2BC=16cm,t=8;
③当BP=AP时,AP=BP=2tcm,CP=|2t 8|cm,AC=6cm,
在Rt△ACP中,AP2=AC2+CP2,
所以(2t)2=62+(2t 8)2,
解得:t=,
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=.
【点睛】本题考查了勾股定理以及等腰三角形的知识,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.
14.C
【详解】解:如图所示,∵(a+b)2=21
∴a2+2ab+b2=21,
∵大正方形的面积为13,即:a2+b2=13,
∴2ab=21﹣13=8,
∴小正方形的面积为13﹣8=5.
故选C.
15.B
【详解】解:A中,根据勾股定理以及正方形的面积公式即可得到,正确;
B中,根据A,C联立结合完全平方公式可以求得x+y=,错误.
C中,根据四个直角三角形的面积和加上小正方形的面积即可得到,正确;
D中, 根据小正方形的边长是4即可得到,正确;
故选B.
16.(1)见解析;(2)见解析;(3)在四边形ABCD中,AB⊥BC,DC⊥BC,AD比AB长0.5米,BC=4米,CD=0.5米,求AB的长;8米
【分析】(1)将图1分割成五块:四个直角边分别为1、2的直角三角形,一个边长为2的正方形,再在图2中,拼成边长为的正方形即可.
(2)根据20个小正方形的面积的和等于拼成的正方形的面积,根据勾股定理确定截线的长度即可;
(3)根据题意,画出图形,可将该问题抽象为解直角三角形问题,该直角三角形的斜边比其中一条直角边多1m,而另一条直角边长为5m,可以根据勾股定理求出斜边的长即可.
【详解】解:(1)如图
(2)
=
=
∴
(3)如图,在四边形ABCD中,AB⊥BC,DC⊥BC,AD比AB长0.5米,BC=4米,CD=0.5米,求AB的长.
解:过点D作DE⊥AB,垂足为E
∵ AB⊥BC,DC⊥BC
∴∠B=∠C=∠DEB=90
∴四边形BCDE是矩形
∴ED=BC=4,BE=DC=0.5
设AB=,则AD=+0.5,AE=-0.5
在RtΔAED中
AD2=AE2+ED2
(+0.5)2=(-0.5)2+42
解得:=8
答:旗杆的高为8米.
【点睛】本题考查作图的运用及设计作图和勾股定理的应用,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
17.(1)见解析
(2)少0.05千米
(3)
【分析】(1)梯形的面积可以由梯形的面积公式求出,也可利用三个直角三角形面积求出,两次求出的面积相等列出关系式,化简即可得证;
(2)设,则,根据勾股定理列方程,解得即可得到结果;
(3)在和中,由勾股定理得求出,列出方程求解即可得到结果.
【详解】(1)解:梯形的面积为,
也可以表示为,
∴,
即;
(2)∵,
∴,
在中,,
即,
解得,
即,
(千米),
答:新路比原路少0.05千米;
(3)设,则,
在中,,
在中,,
∴,
即,
解得:.
【点睛】此题主要考查了勾股定理的证明与应用,一元一次方程,熟练掌握相关定理是解答此题的关键.
18.B
【分析】勾股数,一般是指能够构成直角三角形三条边的三个正整数.根据直角三角形中斜边的长度大于另外两条直角边中任意一条边的长度,且斜边的平方等于两条直角边平方的和,即可求出答案.
【详解】解:A选项, , 不是正整数,不符合题意;
B选项, , , ,92+402=412符合题意;
C选项,不是正整数 , 不符合题意;
D选项, , , ,22+32≠42不符合题意;
故选:.
【点睛】本题主要考查勾股定理的逆定理,根据两条较小边的平方和等于较大边的平方,则这三条边能组成直角三角形,理解和掌握直角三角形的勾股定理的逆定理是解题的关键.
19.C
【分析】依据每列数的规律,即可得到,进而得出的值.
【详解】解:由题可得:……
当
故选:C
【点睛】本题为勾股数与数列规律综合题;观察数列,找出规律是解答本题的关键.
20.C
【分析】结合题意,根据有理数乘方、有理数加法的性质计算,即可得到答案.
【详解】∵或或
∴7不是广义勾股数,即①正确;
∵
∴13是广义勾股数,即②正确;
∵,,不是广义勾股数
∴③错误;
设
则
当ad=bc或ac=bd时,两个广义勾股数的积不—定是广义勾股数,如2和2都是广义勾股数,但2×2=4,4不是广义勾股数,故④结论错误;
故①②正确
故选:C.
【点睛】本题考查了有理数运算的知识;解题的关键是熟练掌握有理数乘方、有理数加法的性质,从而完成求解.
21.(1)8,10;24,25
(2)①另外两个数为5、13;②证明见解析
【分析】(1)根据勾股数的定义解决此题.
(2)①根据题干中法则Ⅰ解决此题.
②根据整式的运算以及勾股数的定义解决此题.
【详解】(1)勾股数分别为6,8,10;7,24,25.
故答案为:8,10;24,25.
(2)①根据法则Ⅰ,则或.
或(不是奇数,舍去).
.
.
另外两个数为5、13.
②选择法则Ⅰ,证明过程如下:
.
.
选择法则Ⅱ,证明过程如下:
.
.
【点睛】本题主要考查勾股数、勾股定理、整式的运算,熟练掌握勾股数、勾股定理、整式的运算是解决本题的关键.
22.C
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【详解】解:A、,不能构成直角三角形,不符合题意;
B、,不能构成直角三角形,不符合题意;
C、,能构成直角三角形,符合题意;
D、,不能构成直角三角形,不符合题意.
故本题选:C.
【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
23.A
【分析】设出正方形的边长,利用勾股定理,解出各自的长度,再由勾股定理的逆定理分别验算,看哪三条边能够成直角三角形.
【详解】解:设小正方形的边长为1,
则,,,,
因为,
所以能构成一个直角三角形三边的线段是.
故选:A.
【点睛】本题主要考查了勾股定理以及勾股定理的逆定理的应用,熟练掌握勾股定理及其逆定理是解题的关键.
24.C
【分析】根据勾股定理的逆定理逐个判断即可.
【详解】解:∵,,
∴,
∴①可以使△ABC为直角三角形;
∵,,
∴,
∴②不可以使△ABC为直角三角形;
∵,,
∴,
∴③可以使△ABC为直角三角形;
∵,,
∴,
∴④可以使△ABC为直角三角形,
综上所述,共有3组可以使△ABC为直角三角形.
故选:C.
【点睛】此题考查了勾股定理的逆定理,解题的关键是熟练掌握勾股定理的逆定理.
25.(1)当时,;
(2)是直角三角形,理由见解析
【分析】(1)根据题意可得:,再根据线段中点的定义可得,从而可得,,由等腰三角形的性质得,则建立方程即可解答;
(2)当时,,,然后分别在和中,利用勾股定理求出和,最后利用勾股定理的逆定理证明是直角三角形,即可解答.
【详解】(1)解:由题意得:,
∵F为的中点,
∴,
∵,,
∴,,
∵,,
∴,
即,
解得:,
∴当时,;
(2)解:是直角三角形,
理由:当时,,
∴,
在中,,
在中,,
∵,,
∴,
∴是直角三角形.
【点睛】本题考查了勾股定理,勾股定理的逆定理,等腰三角形的性质,熟练掌握勾股定理,以及勾股定理的逆定理是解题的关键.
26.B
【分析】根据勾股定理的逆定理可以判断的形状,然后再根据,,即可得到四边形是矩形,根据矩形的性质可以得到,要求的最小值,只要求得的最小值即可,然后根据垂线段最短,即可得到的最小值,从而可以得到的最小值.
【详解】解:,,,
,
是直角三角形,,
又,,
四边形是矩形,
如图,连接,
,
当时,取得最小值,
此时,解得:,
的最小值是,
,
的取值范围为:,
故选:B.
【点睛】此题考查勾股定理的逆定理,关键是根据勾股定理的逆定理可以判断的形状解答.
27.45
【分析】如图,连接ME、DE,可知∠MAB=∠EDF,∠MDC﹣∠MAB=∠MDC﹣∠EDF=∠EDM,勾股定理计算得到△EMD是等腰直角三角形,进而求出角的值.
【详解】解:如图,连接ME、DE
可知∠MAB=∠EDF
∴∠MDC﹣∠MAB=∠MDC﹣∠EDF=∠EDM
∵ME,MD,DE
∴ME=MD,ME2+MD2=DE2
∴△EMD是等腰直角三角形
∴∠MDE=45°
即∠MDC﹣∠MAB=45°
故答案为:45.
【点睛】本题考查了勾股定理,等腰三角形.解题的关键在于找出角度之间的数量关系.
28.##45度
【分析】连接,,设与交于点,根据勾股定理的逆定理先证明是等腰直角三角形,从而可得,再根据题意可得,然后利用三角形的外角,进行计算即可解答.
【详解】解:如图:连接,,设与交于点,
由题意得:
,
,
,
,,
是等腰直角三角形,
,
,
,,
,
,
,
是的一个外角,
,
,
故答案为:.
【点睛】本题考查了勾股定理、平行线的性质,勾股定理的逆定理,解题的关键是根据题目的已知条件并结合图形添加适当的辅助线.
29.
【分析】先求出=36,再根据直线外一点到直线上任意一点的距离,垂线段最短,利用三角形面积公式即可求得AP最短时的长,然后即可求出AN最长时的长.
【详解】解:∵四边形的面积为18,,
∴,即=36,
在中,,,,
∴∠BAC=90°,
∵点为的中点,
∴AN=DE,
∴DE最大时,AN最大,
∵,
∴AP最小时,DE最大,即AP⊥BC时,AP最小,
∵AP=,
∴DE=,
∴,
故答案为:.
【点睛】此题考查了勾股定理逆定理的应用,直线外一点到直线上任一点的距离,垂线段最短的知识点,解题的关键是理解AP最短时DE最大,即AN最大.
30.
【分析】连接,根据勾股定理求出的长,然后运用勾股定理逆定理证明是直角三角形,然后根据即可得出答案.
【详解】:连接,
,,,
,
,即,
是直角三角形,且,
.
【点睛】本题考查了勾股定理以及其逆定理,作出辅助线构造直角三角形是解本题的关键.
31.(1)见解析
(2)
【分析】(1)连接,根据平分线的性质可得,运用勾股定理逆定理即可得出结果;
(2)设,则,然后根据勾股定理进行计算即可.
【详解】(1)证明:连接,
∵边上的垂直平分线为,
∴,
∵,
∴,
∴,
∴;
(2)解:设,则,
在中,,
∴,
解得:,
∴的长为.
【点睛】本题考查了垂直平分线的性质、勾股定理以及勾股定理逆定理,熟练掌握相关性质定理是解本题的关键.
32.B
【分析】先将立体图形展开转化为平面图形,再根据“两点之间,线段最短”、勾股定理即可求得结论.
【详解】解:沿将圆柱体的侧面展开,如图:
∵底面半径是
∴
∴在中,,
∴.
故选:B
【点睛】本题考查了立体图形转化为平面图形、线段公理的应用以及勾股定理等知识点,能将立体几何问题转化为平面几何问题是解决问题的关键.
33.4.55
【分析】根据题意结合勾股定理得出折断处离地面的长度即可.
【详解】解:设折断处离地面尺,根据题意可得:
,
解得:,
答:折断处离地面4.55尺.
故答案为:4.55.
【点睛】此题主要考查了勾股定理的应用,解题的关键是根据题意正确应用勾股定理列出等式进行求解.
34.7cm≤h≤9cm.
【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.
【详解】
如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24 15=9cm;
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=8cm,BD=15cm,
∴AB= ==17cm,
∴此时h=24 17=7cm,
所以h的取值范围是7cm h 9cm.
故答案为7cm≤h≤9cm.
【点睛】本题考查勾股定理的应用.
35.CE=13.3km.
【分析】设CE=xkm,则DE=(20﹣x)km,由AE=BE根据勾股定理可得关于x的方程,解方程即得结果.
【详解】解:设CE=x km,则DE=(20﹣x)km.
在Rt△ACE中,由勾股定理得:AE2=AC2+CE2=82+x2,
在Rt△BDE中,由勾股定理得:BE2=BD2+DE2=142+(20﹣x)2,
由题意可知:AE=BE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3,
所以CE=13.3km.
【点睛】本题考查了勾股定理的应用,属于基本题型,正确理解题意、熟练掌握勾股定理是解题的关键.
36.(1)2.4m;(2)1.3m.
【详解】试题分析:(1)在直角三角形ABC中,利用勾股定理即可求出AC的长;
(2)首先求出AC的长,利用勾股定理可求出B′C的长,进而得到BB′=CB′-CB的值.
试题解析:(1)在Rt△ABC中,由勾股定理,得AC2+BC2=AB2,
∴AC2+0.72=2.52,
解得AC=2.4(m),
答:此时梯顶距地面的高度AC为2.4m;
(2)由题意得:A′C=2.4-0.9=1.5,A′B′=2.5,
在Rt△A′B′C中,由勾股定理得A′C2+B′C2=A′B′2,
∴1.52+B′C2=2.52.
解得B′C =2(m),
∴BB′= B′C-BC=2-0.7=1.3(m),
答:梯足在水平方向向右滑动了1.3m.
37.(1)着火点C受洒水影响,理由见解析;(2)能,理由见解析
【分析】(1)过点作,垂足为,勾股定理的逆定理证明是直角三角形,进而等面积法求得长度,与500进行比较即可求得答案;
(2)以点为圆心,500m为半径作圆,交于点,勾股定理求得,进而求得的长,根据飞机的速度得到飞行时间,再根据题意求得灭火时间,即可解决问题.
【详解】(1)着火点C受洒水影响,理由如下,
如图,过点作,垂足为,
,
是直角三角形
着火点C受洒水影响
(2)如图,以点为圆心,500m为半径作圆,交于点
则
在中,
着火点C能被扑灭.
【点睛】本题考查了勾股定理与勾股定理的逆定理的应用,等腰三角形的性质,根据题意作出图形是解题的关键.
38.16
【分析】由弦图推出即可证明,,再根据四边形为正方形,得到,从而得到点K为正方形的中心,过点K作于点M,由勾股定理得设,则,最后用a,b表示出,将的值代入即可求解.
【详解】解:在弦图中,,
∵四边形是正方形,
∴,,
∴,
∴,
∵,
∴,
∴
∵,
∴,
在和中,
,
∴,
∴,
∵四边形为正方形,
∴,即,
在和中,
,
∴,
∴,即点K为正方形的中心,
如图,过点K作于点M,
∵,
∴,
在中,
由勾股定理得,
∴,
则,
设,则,
∴=,
=,
∴.
故答案为:16.
【点睛】本题主要考查全等三角形的判定与性质,勾股定理,三角形的面积,正方形的性质,解题的关键是寻找全等三角形的条件解决问题.
39. 或20或 或
【分析】分情况讨论,由等腰三角形的判定与性质分别求解即可.
【详解】解:∵∠ACB=90°,
∴△ABC是直角三角形,
在Rt△ABC中,由勾股定理得:AB13,
当点P在AC上时,CP=CB=5,
∴t=5;
当点P在AB上时,分三种情况:
①当BP=BC=5,如图1所示:
则AP=13﹣5=8,
∴t=12+8=20;
②当CP=CB=5时,
过点C作CM⊥AB于M,如图2所示:
则,
∵,
∴CM,
在Rt△BCM中,由勾股定理得:BM,
∴BP=2BM
∴AP=13,
∴t=12;
③当PC=PB时,如图3所示:
则∠B=∠BCP,
∵∠B+∠A=90°,∠BCP+∠ACP=90°,
∴∠A=∠ACP,
∴AP=PC,
∴AP=PBAB,
∴t=12;
综上所述,当t=5或20或或时,△BCP为等腰三角形.
【点睛】本题考查了勾股定理、等腰三角形的判定与性质以及三角形面积等知识,熟练掌握勾股定理和等腰三角形的判定与性质是解题的关键.
40.(1)
(2),16,5
(3)5或11
【分析】(1)根据动点的运动速度和时间先求出,再根据勾股定理即可求解;
(2)根动点运动过程中形成三种等腰三角形,分3种情况即可求解;
(3)根据动点运动的不同位置,分2种情况利用全等三角形的判定与性质和勾股定理即可求解.
【详解】(1)解:根据题意,得,
在中,根据勾股定理,得.
答:的长为.
(2)在中,,
根据勾股定理,得
若,则 ,解得;
若,则,解得;
若,则,解得.
答:当为等腰三角形时,t的值为,16,5.
(3)①点P在线段上时,过点D作于E,连接,如图1所示:
则,
∴,
∴平分,
∴,
又∵,
∴,
∴,
∴,
∴,
∴,
在中,由勾股定理得:,
解得:;
②点P在线段的延长线上时,过点D作于E,连接,如图2所示:
同①得:,
∴,
∴,
∴,
∴,
在中,由勾股定理得:,
解得:;
综上所述,在点P的运动过程中,当t的值为5或11时,能使.
【点睛】本题考查了等腰三角形的性质,全等三角形的判定与性质,勾股定理,解决本题的关键是动点运动到不同位置形成不同的等腰三角形.
答案第1页,共2页
答案第1页,共2页
勾股定理——面积问题
(2022·宿迁期中)
1.如图,、、分别是以的三边为直径所画半圆的面积,其中,,则 .
(2022·连云港期中)
2.如图,在四边形中,,分别以四边形的四条边为边长,向外作四个正方形,面积分别为,,和.若,,,则的值是 .
(2022·扬州期中)
3.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、6、20,则正方形B的面积为) .
(2022·镇江期中)
4.如图,在中,,分别以、、为边向上作正方形,已知的面积为,则图中阴影部分面积之和为 .
勾股定理——距离问题
(2022·南京期中)
5.如图,在中,,,,则点A到的距离是( )
A.10 B.11 C.12 D.13
(2022·南通期中)
6.如图,网格中的每个小正方形的边长为1,的顶点A、B、C均在网格的格点上,于点D,则BD的长为( )
A. B. C. D.
(2022·无锡期中)
7.如图,,已知中,,,的顶点A、B分别在边、上,当点B在边上运动时,点A随之在边上运动,的形状保持不变,在运动过程中,点C到点O的最大距离为( )
A.5 B.6 C.7 D.8
8.如图,,动点A和C分别在射线OP、OQ上运动,且,作,且.在运动过程中,OB的最大距离是( )
A.5cm B. C. D.3cm
勾股定理——折叠问题
(2022·常州期中)
9.如图,在矩形ABCD中,,.点E是边BC上一点,沿AE翻折,点B恰好落在CD边上点F处,则CE的长是( )
A. B. C. D.3
(2022·盐城期中)
10.如图,把四边形EDFB纸片分别沿AB和DC折叠,恰好使得点E和点D、点F和点B重合,在折叠成的新四边形ABCD中,,,则的面积是 .
勾股定理——特殊三角形的存在性问题2
(2022·苏州期中)
11.如图,在△ABC中,,D为BC边上一点,且,,,点E是AB边上的动点,连接DE.
(1)求AB的长;
(2)当△BDE是直角三角形时,求AE的长.
(2022·盐城期中)
12.如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
(2022·常州期中)
13.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
勾股定理的证明(含以弦图为背景的计算)
(2022·苏州期中)
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
(2022·无锡期中)
15.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为81,小正方形面积为16,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( )
A.x2+y2=81 B.x+y=13 C.2xy+16=81 D.x-y=4
(2022·常州期中)
16.(1)图1是由有20个边长为1的正方形组成的,把它按图1的分割方法分割成5部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图2的网格中画出拼接成的大正方形.
(2)如果(1)中分割成的直角三角形两直角边分别为a,b斜边为c.请你利用图2中拼成的大正方形证明勾股定理.
(3)应用:测量旗杆的高度:校园内有一旗杆,小希想知道旗杆的高度,经观察发现从顶端垂下一根拉绳,于是他测出了下列数据:①测得拉绳垂到地面后,多出的长度为0.5米;②他在距离旗杆4米的地方拉直绳子,拉绳的下端恰好距离地面0.5米.请你根据所测得的数据设计可行性方案,解决这一问题.(画出示意图并计算出这根旗杆的高度).
(2022·扬州期中)
17.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为),也可以表示为,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路,且.测得千米,千米,求新路比原路少多少千米?
(3)在第(2)问中若时,,,,,设,求x的值.
勾股数
(2022·苏州期中)
18.以下数组中,其中是勾股数的是( )
A. , , B.9 ,40 , 41
C.1 , ,1 D.2 ,3 ,4
(2022·连云港期中)
19.如果正整数a、b、c满足等式,那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )
A.47 B.62 C.79 D.98
(2022·南通期中)
20.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即,那么称m为广义勾股数.则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( )
A.②④ B.①②④ C.①② D.①④
(2022·扬州期中)
21.同学们都知道,凡是可以构成一个直角三角形三边的一组正整数,称之为“勾股数”.比如3,4,5或11,60,61等.
(1)请你写出另外两组勾股数:6,_____,_____;7,_____,_____;
(2)清朝的扬州籍数学家罗士琳提出了四个构造勾股数的法则,其中有两个法则如下:
(Ⅰ)如果是大于1的奇数,那么,,是一组勾股数
(Ⅱ)如果是大于2的偶数,那么,,是一组勾股数
①如果在一组勾股数中,其中有一个数为12,根据法则(Ⅰ)求出另外两个数;
②请证明两个法则的正确性.
勾股定理的逆定理——直角三角形的判定
(2022·泰州期中·改编)
22.下列各组线段能构成直角三角形的一组是( )
A.,, B.,,
C.,, D.,,
(2022·常州期中)
23.如图,在由单位正方形组成的网格图中标有四条线段,其中能构成一个直角三角形三边的线段是( )
A. B. C. D.
(2022·无锡/盐城期中)
24.以下四组代数式作为△ABC的三边,能使△ABC为直角三角形的有:①3n,4n,5n,(n为正整数);②n,n+1,n+2(n为正整数);③n2-1,2n,n2+1(n≥2,n为正整数);④m2-n2,2mn,m2+n2(m>n,m,n为正整数) ( )
A.1组 B.2组 C.3组 D.4组
(2022·泰州期中)
25.如图,,垂足为D,且,.点E从B点沿射线向右以2个单位/秒的速度匀速运动,F为的中点,连接,设点E运动的时间为t.
(1)当t为何值时,;
(2)当时,判断的形状,并说明理由.
勾股定理的逆定理——直角三角形的判定与性质
(2022·常州期中)
26.如图,在中,,,,为边上一动点,于,于,则的取值范围为( )
A. B. C. D.
(2022·无锡期中)
27.如图所示的是正方形网格,则∠MDC﹣∠MAB= °(点A,B,C,D,M.网格线交点).
(2022·常州期中)
28.如图,正方形网格中每一个小正方形的边长为1,小正方形的顶点为格点,点,,为格点,点为与网格线的交点,则 .
(2022·镇江期中)
29.如图,已知在中,,,,为边上一个动点,连接,,分别交、于点、,垂足为,点为的中点,若四边形的面积为18,则的最大值为 .
(2022·宿迁期中)
30.图,四边形中,,,,,,求四边形的面积.
(2022·南京期中)
31.如图,在中,边上的垂直平分线与分别交于点和,且.
(1)求证:;
(2)若,,求的长.
勾股定理的实际应用
32.如图,一圆柱高,底面半径为,一只蚂蚁从点爬到点处吃食,要爬行的最短路程(取3)是( )
A. B. C. D.无法确定
(2022·南京/无锡/常州/南通期中)
33.在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何 它的意思是:一根竹子原高一丈(尺),中部一处折断,竹梢触地面处离竹根尺,试问折断处离地面 尺.
(2022·常州/苏州/淮安期中)
34.将一根24cm的筷子置于底面直径为8cm,高为15cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是 .
(2022·南通期中)
35.如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km,B村庄到公路的距离BD=14km,测得C、D两点的距离为20km,现要在CD之间建一个服务区E,使得A、B两村庄到E服务区的距离相等,求CE的长.
(2022·盐城期中)
36.一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
(2022·淮安期中)
37.森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点, 且点 C与直线 AB上两点A,B的距离分别为600m和800m,又AB=1000m,飞机中心周围500m 以内可以受到洒水影响.
(1)着火点C受洒水影响吗?为什么?
(2)若飞机的速度为10 m/s,要想扑灭着火点C估计需要13秒,请你通过计算判断着火点C能否被扑灭?
(2022·苏州期中)
38.如图,在弦图中,正方形的对角线与正方形的对角线交于点K,对角线交正方形于G,J两点,记面积为,面积为,若,则的值为 .
(2022·南通期中)
39.如图△ABC中,∠ACB=90°,AC=12,BC=5.若动点P从点C开始以每秒1个单位的速度,按C→A→B的路径运动,设运动的时间为t秒,当t为 时,△BCP为等腰三角形.
(2022·无锡期中)
40.如图,已知在中,,D是上的一点,,点P从B点出发沿射线方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连接.
(1)当秒时,求的长度(结果保留根号);
(2)当为等腰三角形时,求t的值;
(3)过点D作于点E.在点P的运动过程中,当t为何值时,能使?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.
【分析】先分别算出、、的面积,然后根据勾股定理即可解答.
【详解】解:∵,,
∴
∵
∴.
∵,,
∴
故答案为.
【点睛】本题主要考查了勾股定理的应用,勾股定理的内容是直角三角形的两条直角边的平方和等于斜边的平方.
2.8
【分析】连接AC,构造和,然后在中利用勾股定理求出,在中求出,进而求得的值.
【详解】解:如图所示,连接,
在中,,
即;
同理,在中,,
即,
则.
故答案为:8.
【点睛】本题考查勾股定理,解决本题的关键是将面积转化为勾股定理求边长平方即可.
3.10
【分析】根据勾股定理的几何意义:解得即可.
【详解】解:如图,
由题意:,
∵正方形A、C、D的面积依次为4、6、20,
∴,
∴.
故答案为:10.
【点睛】本题考查了勾股定理,要熟悉勾股定理的几何意义,知道直角三角形两直角边的平方和等于斜边的平方.
4.
【分析】利用勾股定理和正方形的面积公式可得,利用正方形的性质证明和,根据全等三角形的面积相等,从而得出,,再根据三个正方形面积的关系可得出,从而可得阴影面积之和.
【详解】解:如图,设,,,
∵在中,,
∴,
∵四边形,四边形和四边形都是正方形,
∴,,,
∴,
∵四边形和四边形是正方形,
∴,,,
∴是直角三角形,
在和中,
,
∴
∴,
∵四边形和四边形是正方形,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∵,
又∵,
,
,
∴,
∴,
∴图中阴影部分面积之和为.
故答案为:.
【点睛】本题考查正方形的性质,勾股定理,全等三角形的判定和性质,等角的余角相等等知识,运用了等积变换的思想方法.运用等积变换是解题的关键.
5.C
【分析】过点作交的延长线于点,根据勾股定理求得,进而勾股定理求得,即可求解.
【详解】解:如图,过点作交的延长线于点,
∴,
∵,,,
∴
∴
解得:,
∴,
即点A到的距离是.
故选:C.
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
6.C
【分析】通过面积相等法求解即可.
【详解】解:如图所示:
,
∵,
即,
解得:.
故选:C.
【点睛】本题考查网格内求面积,想到是关键.
7.C
【分析】由先等腰三角形的性质得,由勾股定理求出,再由三角形的三边关系得,则当O、D、C共线时,OC有最大值,最大值是,然后由直角三角形斜边上的中线性质求出,即可解决问题.
【详解】解:取的中点D,连接,如图所示:
∵,,
∵点D是AB边中点,
∴,
∴,
连接OD,OC,有,
当共线时,有最大值,最大值是,
又∵为直角三角形,D为斜边的中点,
∴,
∴,
即点C到点O的最大距离为7,
故选:C.
【点睛】此题考查的是勾股定理,等腰三角形的性质,直角三角形斜边上的中线性质以及三角形的三边关系等知识,证出OC最大时的长为CD+OD是解本题的关键.
8.B
【分析】取AC中点D,连接BD,OD,根据数形结合分析可知,根据B,O,D的位置关系求OB的最大距离.
【详解】解:取AC中点D,连接BD,OD,
∵,D为AC中点,
∴,,
在中,,
∴,
由图像可知,
当B,O,D三点共线时,等号成立,
∴OB的最大距离是.
故选:B.
【点睛】本题考查了动点和定点距离的最大值和直角三角形斜边的中线等于斜边的一半,解决本题的关键是分析B,O,D的位置关系.
9.B
【分析】根据折叠的性质可知,AF=AB=10,根据勾股定理求出DF,进而求出CF;在根据勾股定理即可得,列出等式求解即可.
【详解】∵△AFE由△ABE沿AE翻折得到;
∴△AFE≌△ABE,
∴AF=AB=10,EF=BE
在Rt△ADF中,由勾股定理可得:,
∵四边形ABCD为矩形,
∴CD=AB=10,
∴CF=CD-DF=10-8=2,
设CE=x,则BE=EF=6-x,
在Rt△CEF中,由勾股定理可得:,
解得:x=,
故选:B
【点睛】本题主要考查了勾股定理、折叠的性质以及矩形的性质,熟练地掌握矩形的性质和折叠的性质,根据勾股定理列出等式是解题的关键.
10.
【分析】先由勾股定理求出BD,DC的长,过点F作FHED交ED的延长线于H,再证,得到FH=AD=3,由SBEF=S四边形BEDF-SEDF即可得到答案.
【详解】解:∵ABD是由ABE折叠而成,BDC是由FDC折叠而成,
∴BE=BD,EA=AD,BC=FC,BD=DF,
∴BAED, DCBF,BE=BD=DF,,
∵AD=3,AB=4,BC=,
∴BD=,
∴,
∴BCD=DBC=45
∴ BDF=90,
如图,过点F作FHED交ED的延长线于H,
∵ABD+ADB=90,FDH+ADB=90,
∴ABD=FDH,
∴在ABD和HDF中,
∴,
∴FH=AD=3,
∴SBEF=S四边形BEDF-SEDF= SEBD+SDBF- SEDF
=.
【点睛】此题主要考查了勾股定理,轴对称的性质,全等三角形的判定与性质及三角形的面积,正确的添加辅助线证明三角形全等是解决问题的关键.
11.(1)
(2)AE的长为或3
【分析】(1)先根据勾股定理证明△ACD是直角三角形,且,求得,然后根据勾股定理直接计算即可求解.
(2)根据等边对等角以及直角三角形的两锐角互余可得,根据△BDE是直角三角形需分两种情况分析:①当时,,②当时,根据勾股定以及等面积法即可求解.
【详解】(1)解:在△ACD中,∵,,,
∴,
∴△ACD是直角三角形,且,
∵,
∴,
∴在Rt△ACB中,;
(2)∵,,
∴,
∴△BDE是直角三角形需分两种情况分析:
①当时,,
∴在Rt△BDE中,,
∴;
②当时,,即,
解得:,
∴,
∴;
综上所述,AE的长为或3.
【点睛】本题考查了勾股定理与勾股定理的逆定理,等腰三角形的性质,掌握勾股定理是解题的关键.
12.(1)t=;(2)t=;
【分析】(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4-2t,根据勾股定理列方程即可得到结论;
(2)当点P在∠CAB的平分线上时,如图,过点P作PE⊥AB于点E,此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,根据勾股定理列方程即可得到结论.
【详解】(1)设存在点P,使得PA=PB,此时PA=PB=2t,
在Rt△ABC中,AC===4,PC=4–2t,
在Rt△PCB中,PC2+CB2=PB2,即:(4–2t)2+32=(2t)2,
解得t=,
∴当t=时,PA=PB;
(2)当点P在∠BAC的平分线上时,如图,过点P作PE⊥AB于点E,
此时BP=7–2t,PE=PC=2t–4,BE=5–4=1,
在Rt△BEP中,PE2+BE2=BP2,
即:(2t–4)2+12=(7–2t)2,解得t=,
∴当t=时,P在∠BAC的平分线上.
【点睛】本题考查的是三角形的综合运用,熟练掌握勾股定理是解题的关键.
13.(1)8cm;(2)4或;(3)5或8或.
【分析】(1)直接根据勾股定理求出BC的长度;
(2)当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
(3)当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP时,分别求出BP的长度,继而可求得t值.
【详解】解:(1)在Rt△ABC中,BC2=AB2 AC2=102 62=64,
∴BC=8(cm);
(2)由题意知BP=2tcm,
①当∠APB为直角时,点P与点C重合,BP=BC=8cm,即t=4;
②当∠BAP为直角时,BP=2tcm,CP=(2t 8)cm,AC=6cm,
在Rt△ACP中,AP2=62+(2t 8)2,
在Rt△BAP中,AB2+AP2=BP2,
即:102+[62+(2t 8)2]=(2t)2,
解得:t=,
故当△ABP为直角三角形时,t=4或t=;
(3)①当AB=BP时,t=5;
②当AB=AP时,BP=2BC=16cm,t=8;
③当BP=AP时,AP=BP=2tcm,CP=|2t 8|cm,AC=6cm,
在Rt△ACP中,AP2=AC2+CP2,
所以(2t)2=62+(2t 8)2,
解得:t=,
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=.
【点睛】本题考查了勾股定理以及等腰三角形的知识,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.
14.C
【详解】解:如图所示,∵(a+b)2=21
∴a2+2ab+b2=21,
∵大正方形的面积为13,即:a2+b2=13,
∴2ab=21﹣13=8,
∴小正方形的面积为13﹣8=5.
故选C.
15.B
【详解】解:A中,根据勾股定理以及正方形的面积公式即可得到,正确;
B中,根据A,C联立结合完全平方公式可以求得x+y=,错误.
C中,根据四个直角三角形的面积和加上小正方形的面积即可得到,正确;
D中, 根据小正方形的边长是4即可得到,正确;
故选B.
16.(1)见解析;(2)见解析;(3)在四边形ABCD中,AB⊥BC,DC⊥BC,AD比AB长0.5米,BC=4米,CD=0.5米,求AB的长;8米
【分析】(1)将图1分割成五块:四个直角边分别为1、2的直角三角形,一个边长为2的正方形,再在图2中,拼成边长为的正方形即可.
(2)根据20个小正方形的面积的和等于拼成的正方形的面积,根据勾股定理确定截线的长度即可;
(3)根据题意,画出图形,可将该问题抽象为解直角三角形问题,该直角三角形的斜边比其中一条直角边多1m,而另一条直角边长为5m,可以根据勾股定理求出斜边的长即可.
【详解】解:(1)如图
(2)
=
=
∴
(3)如图,在四边形ABCD中,AB⊥BC,DC⊥BC,AD比AB长0.5米,BC=4米,CD=0.5米,求AB的长.
解:过点D作DE⊥AB,垂足为E
∵ AB⊥BC,DC⊥BC
∴∠B=∠C=∠DEB=90
∴四边形BCDE是矩形
∴ED=BC=4,BE=DC=0.5
设AB=,则AD=+0.5,AE=-0.5
在RtΔAED中
AD2=AE2+ED2
(+0.5)2=(-0.5)2+42
解得:=8
答:旗杆的高为8米.
【点睛】本题考查作图的运用及设计作图和勾股定理的应用,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
17.(1)见解析
(2)少0.05千米
(3)
【分析】(1)梯形的面积可以由梯形的面积公式求出,也可利用三个直角三角形面积求出,两次求出的面积相等列出关系式,化简即可得证;
(2)设,则,根据勾股定理列方程,解得即可得到结果;
(3)在和中,由勾股定理得求出,列出方程求解即可得到结果.
【详解】(1)解:梯形的面积为,
也可以表示为,
∴,
即;
(2)∵,
∴,
在中,,
即,
解得,
即,
(千米),
答:新路比原路少0.05千米;
(3)设,则,
在中,,
在中,,
∴,
即,
解得:.
【点睛】此题主要考查了勾股定理的证明与应用,一元一次方程,熟练掌握相关定理是解答此题的关键.
18.B
【分析】勾股数,一般是指能够构成直角三角形三条边的三个正整数.根据直角三角形中斜边的长度大于另外两条直角边中任意一条边的长度,且斜边的平方等于两条直角边平方的和,即可求出答案.
【详解】解:A选项, , 不是正整数,不符合题意;
B选项, , , ,92+402=412符合题意;
C选项,不是正整数 , 不符合题意;
D选项, , , ,22+32≠42不符合题意;
故选:.
【点睛】本题主要考查勾股定理的逆定理,根据两条较小边的平方和等于较大边的平方,则这三条边能组成直角三角形,理解和掌握直角三角形的勾股定理的逆定理是解题的关键.
19.C
【分析】依据每列数的规律,即可得到,进而得出的值.
【详解】解:由题可得:……
当
故选:C
【点睛】本题为勾股数与数列规律综合题;观察数列,找出规律是解答本题的关键.
20.C
【分析】结合题意,根据有理数乘方、有理数加法的性质计算,即可得到答案.
【详解】∵或或
∴7不是广义勾股数,即①正确;
∵
∴13是广义勾股数,即②正确;
∵,,不是广义勾股数
∴③错误;
设
则
当ad=bc或ac=bd时,两个广义勾股数的积不—定是广义勾股数,如2和2都是广义勾股数,但2×2=4,4不是广义勾股数,故④结论错误;
故①②正确
故选:C.
【点睛】本题考查了有理数运算的知识;解题的关键是熟练掌握有理数乘方、有理数加法的性质,从而完成求解.
21.(1)8,10;24,25
(2)①另外两个数为5、13;②证明见解析
【分析】(1)根据勾股数的定义解决此题.
(2)①根据题干中法则Ⅰ解决此题.
②根据整式的运算以及勾股数的定义解决此题.
【详解】(1)勾股数分别为6,8,10;7,24,25.
故答案为:8,10;24,25.
(2)①根据法则Ⅰ,则或.
或(不是奇数,舍去).
.
.
另外两个数为5、13.
②选择法则Ⅰ,证明过程如下:
.
.
选择法则Ⅱ,证明过程如下:
.
.
【点睛】本题主要考查勾股数、勾股定理、整式的运算,熟练掌握勾股数、勾股定理、整式的运算是解决本题的关键.
22.C
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【详解】解:A、,不能构成直角三角形,不符合题意;
B、,不能构成直角三角形,不符合题意;
C、,能构成直角三角形,符合题意;
D、,不能构成直角三角形,不符合题意.
故本题选:C.
【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
23.A
【分析】设出正方形的边长,利用勾股定理,解出各自的长度,再由勾股定理的逆定理分别验算,看哪三条边能够成直角三角形.
【详解】解:设小正方形的边长为1,
则,,,,
因为,
所以能构成一个直角三角形三边的线段是.
故选:A.
【点睛】本题主要考查了勾股定理以及勾股定理的逆定理的应用,熟练掌握勾股定理及其逆定理是解题的关键.
24.C
【分析】根据勾股定理的逆定理逐个判断即可.
【详解】解:∵,,
∴,
∴①可以使△ABC为直角三角形;
∵,,
∴,
∴②不可以使△ABC为直角三角形;
∵,,
∴,
∴③可以使△ABC为直角三角形;
∵,,
∴,
∴④可以使△ABC为直角三角形,
综上所述,共有3组可以使△ABC为直角三角形.
故选:C.
【点睛】此题考查了勾股定理的逆定理,解题的关键是熟练掌握勾股定理的逆定理.
25.(1)当时,;
(2)是直角三角形,理由见解析
【分析】(1)根据题意可得:,再根据线段中点的定义可得,从而可得,,由等腰三角形的性质得,则建立方程即可解答;
(2)当时,,,然后分别在和中,利用勾股定理求出和,最后利用勾股定理的逆定理证明是直角三角形,即可解答.
【详解】(1)解:由题意得:,
∵F为的中点,
∴,
∵,,
∴,,
∵,,
∴,
即,
解得:,
∴当时,;
(2)解:是直角三角形,
理由:当时,,
∴,
在中,,
在中,,
∵,,
∴,
∴是直角三角形.
【点睛】本题考查了勾股定理,勾股定理的逆定理,等腰三角形的性质,熟练掌握勾股定理,以及勾股定理的逆定理是解题的关键.
26.B
【分析】根据勾股定理的逆定理可以判断的形状,然后再根据,,即可得到四边形是矩形,根据矩形的性质可以得到,要求的最小值,只要求得的最小值即可,然后根据垂线段最短,即可得到的最小值,从而可以得到的最小值.
【详解】解:,,,
,
是直角三角形,,
又,,
四边形是矩形,
如图,连接,
,
当时,取得最小值,
此时,解得:,
的最小值是,
,
的取值范围为:,
故选:B.
【点睛】此题考查勾股定理的逆定理,关键是根据勾股定理的逆定理可以判断的形状解答.
27.45
【分析】如图,连接ME、DE,可知∠MAB=∠EDF,∠MDC﹣∠MAB=∠MDC﹣∠EDF=∠EDM,勾股定理计算得到△EMD是等腰直角三角形,进而求出角的值.
【详解】解:如图,连接ME、DE
可知∠MAB=∠EDF
∴∠MDC﹣∠MAB=∠MDC﹣∠EDF=∠EDM
∵ME,MD,DE
∴ME=MD,ME2+MD2=DE2
∴△EMD是等腰直角三角形
∴∠MDE=45°
即∠MDC﹣∠MAB=45°
故答案为:45.
【点睛】本题考查了勾股定理,等腰三角形.解题的关键在于找出角度之间的数量关系.
28.##45度
【分析】连接,,设与交于点,根据勾股定理的逆定理先证明是等腰直角三角形,从而可得,再根据题意可得,然后利用三角形的外角,进行计算即可解答.
【详解】解:如图:连接,,设与交于点,
由题意得:
,
,
,
,,
是等腰直角三角形,
,
,
,,
,
,
,
是的一个外角,
,
,
故答案为:.
【点睛】本题考查了勾股定理、平行线的性质,勾股定理的逆定理,解题的关键是根据题目的已知条件并结合图形添加适当的辅助线.
29.
【分析】先求出=36,再根据直线外一点到直线上任意一点的距离,垂线段最短,利用三角形面积公式即可求得AP最短时的长,然后即可求出AN最长时的长.
【详解】解:∵四边形的面积为18,,
∴,即=36,
在中,,,,
∴∠BAC=90°,
∵点为的中点,
∴AN=DE,
∴DE最大时,AN最大,
∵,
∴AP最小时,DE最大,即AP⊥BC时,AP最小,
∵AP=,
∴DE=,
∴,
故答案为:.
【点睛】此题考查了勾股定理逆定理的应用,直线外一点到直线上任一点的距离,垂线段最短的知识点,解题的关键是理解AP最短时DE最大,即AN最大.
30.
【分析】连接,根据勾股定理求出的长,然后运用勾股定理逆定理证明是直角三角形,然后根据即可得出答案.
【详解】:连接,
,,,
,
,即,
是直角三角形,且,
.
【点睛】本题考查了勾股定理以及其逆定理,作出辅助线构造直角三角形是解本题的关键.
31.(1)见解析
(2)
【分析】(1)连接,根据平分线的性质可得,运用勾股定理逆定理即可得出结果;
(2)设,则,然后根据勾股定理进行计算即可.
【详解】(1)证明:连接,
∵边上的垂直平分线为,
∴,
∵,
∴,
∴,
∴;
(2)解:设,则,
在中,,
∴,
解得:,
∴的长为.
【点睛】本题考查了垂直平分线的性质、勾股定理以及勾股定理逆定理,熟练掌握相关性质定理是解本题的关键.
32.B
【分析】先将立体图形展开转化为平面图形,再根据“两点之间,线段最短”、勾股定理即可求得结论.
【详解】解:沿将圆柱体的侧面展开,如图:
∵底面半径是
∴
∴在中,,
∴.
故选:B
【点睛】本题考查了立体图形转化为平面图形、线段公理的应用以及勾股定理等知识点,能将立体几何问题转化为平面几何问题是解决问题的关键.
33.4.55
【分析】根据题意结合勾股定理得出折断处离地面的长度即可.
【详解】解:设折断处离地面尺,根据题意可得:
,
解得:,
答:折断处离地面4.55尺.
故答案为:4.55.
【点睛】此题主要考查了勾股定理的应用,解题的关键是根据题意正确应用勾股定理列出等式进行求解.
34.7cm≤h≤9cm.
【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.
【详解】
如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24 15=9cm;
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=8cm,BD=15cm,
∴AB= ==17cm,
∴此时h=24 17=7cm,
所以h的取值范围是7cm h 9cm.
故答案为7cm≤h≤9cm.
【点睛】本题考查勾股定理的应用.
35.CE=13.3km.
【分析】设CE=xkm,则DE=(20﹣x)km,由AE=BE根据勾股定理可得关于x的方程,解方程即得结果.
【详解】解:设CE=x km,则DE=(20﹣x)km.
在Rt△ACE中,由勾股定理得:AE2=AC2+CE2=82+x2,
在Rt△BDE中,由勾股定理得:BE2=BD2+DE2=142+(20﹣x)2,
由题意可知:AE=BE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3,
所以CE=13.3km.
【点睛】本题考查了勾股定理的应用,属于基本题型,正确理解题意、熟练掌握勾股定理是解题的关键.
36.(1)2.4m;(2)1.3m.
【详解】试题分析:(1)在直角三角形ABC中,利用勾股定理即可求出AC的长;
(2)首先求出AC的长,利用勾股定理可求出B′C的长,进而得到BB′=CB′-CB的值.
试题解析:(1)在Rt△ABC中,由勾股定理,得AC2+BC2=AB2,
∴AC2+0.72=2.52,
解得AC=2.4(m),
答:此时梯顶距地面的高度AC为2.4m;
(2)由题意得:A′C=2.4-0.9=1.5,A′B′=2.5,
在Rt△A′B′C中,由勾股定理得A′C2+B′C2=A′B′2,
∴1.52+B′C2=2.52.
解得B′C =2(m),
∴BB′= B′C-BC=2-0.7=1.3(m),
答:梯足在水平方向向右滑动了1.3m.
37.(1)着火点C受洒水影响,理由见解析;(2)能,理由见解析
【分析】(1)过点作,垂足为,勾股定理的逆定理证明是直角三角形,进而等面积法求得长度,与500进行比较即可求得答案;
(2)以点为圆心,500m为半径作圆,交于点,勾股定理求得,进而求得的长,根据飞机的速度得到飞行时间,再根据题意求得灭火时间,即可解决问题.
【详解】(1)着火点C受洒水影响,理由如下,
如图,过点作,垂足为,
,
是直角三角形
着火点C受洒水影响
(2)如图,以点为圆心,500m为半径作圆,交于点
则
在中,
着火点C能被扑灭.
【点睛】本题考查了勾股定理与勾股定理的逆定理的应用,等腰三角形的性质,根据题意作出图形是解题的关键.
38.16
【分析】由弦图推出即可证明,,再根据四边形为正方形,得到,从而得到点K为正方形的中心,过点K作于点M,由勾股定理得设,则,最后用a,b表示出,将的值代入即可求解.
【详解】解:在弦图中,,
∵四边形是正方形,
∴,,
∴,
∴,
∵,
∴,
∴
∵,
∴,
在和中,
,
∴,
∴,
∵四边形为正方形,
∴,即,
在和中,
,
∴,
∴,即点K为正方形的中心,
如图,过点K作于点M,
∵,
∴,
在中,
由勾股定理得,
∴,
则,
设,则,
∴=,
=,
∴.
故答案为:16.
【点睛】本题主要考查全等三角形的判定与性质,勾股定理,三角形的面积,正方形的性质,解题的关键是寻找全等三角形的条件解决问题.
39. 或20或 或
【分析】分情况讨论,由等腰三角形的判定与性质分别求解即可.
【详解】解:∵∠ACB=90°,
∴△ABC是直角三角形,
在Rt△ABC中,由勾股定理得:AB13,
当点P在AC上时,CP=CB=5,
∴t=5;
当点P在AB上时,分三种情况:
①当BP=BC=5,如图1所示:
则AP=13﹣5=8,
∴t=12+8=20;
②当CP=CB=5时,
过点C作CM⊥AB于M,如图2所示:
则,
∵,
∴CM,
在Rt△BCM中,由勾股定理得:BM,
∴BP=2BM
∴AP=13,
∴t=12;
③当PC=PB时,如图3所示:
则∠B=∠BCP,
∵∠B+∠A=90°,∠BCP+∠ACP=90°,
∴∠A=∠ACP,
∴AP=PC,
∴AP=PBAB,
∴t=12;
综上所述,当t=5或20或或时,△BCP为等腰三角形.
【点睛】本题考查了勾股定理、等腰三角形的判定与性质以及三角形面积等知识,熟练掌握勾股定理和等腰三角形的判定与性质是解题的关键.
40.(1)
(2),16,5
(3)5或11
【分析】(1)根据动点的运动速度和时间先求出,再根据勾股定理即可求解;
(2)根动点运动过程中形成三种等腰三角形,分3种情况即可求解;
(3)根据动点运动的不同位置,分2种情况利用全等三角形的判定与性质和勾股定理即可求解.
【详解】(1)解:根据题意,得,
在中,根据勾股定理,得.
答:的长为.
(2)在中,,
根据勾股定理,得
若,则 ,解得;
若,则,解得;
若,则,解得.
答:当为等腰三角形时,t的值为,16,5.
(3)①点P在线段上时,过点D作于E,连接,如图1所示:
则,
∴,
∴平分,
∴,
又∵,
∴,
∴,
∴,
∴,
∴,
在中,由勾股定理得:,
解得:;
②点P在线段的延长线上时,过点D作于E,连接,如图2所示:
同①得:,
∴,
∴,
∴,
∴,
在中,由勾股定理得:,
解得:;
综上所述,在点P的运动过程中,当t的值为5或11时,能使.
【点睛】本题考查了等腰三角形的性质,全等三角形的判定与性质,勾股定理,解决本题的关键是动点运动到不同位置形成不同的等腰三角形.
答案第1页,共2页
答案第1页,共2页
同课章节目录
