第四章 基本平面图形(单元小结)课件(共25张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 第四章 基本平面图形(单元小结)课件(共25张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 828.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
新课标 北师大版
七年级上册
单元小结
第四章
基本平面图形
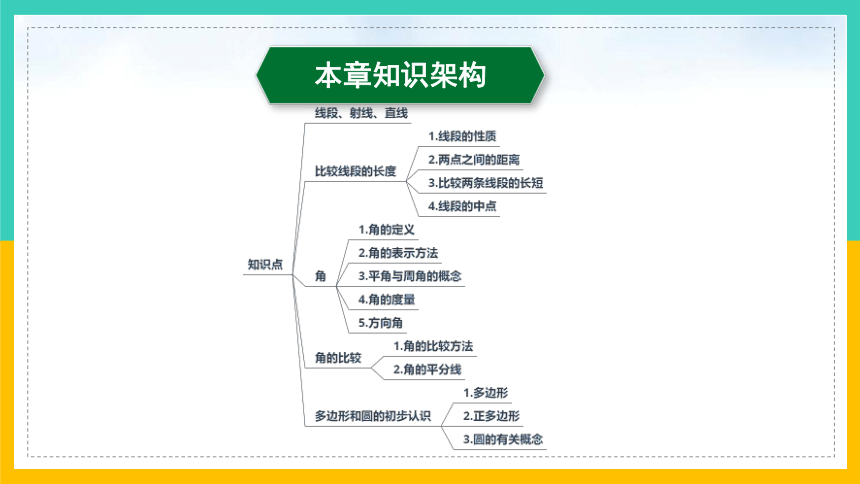
本章知识架构
知识专题
一、线段、射线、直线
1.直线、射线、线段的特点:
类型
线段
射线
直线
端点数
2个
能否延伸
能否度量
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可延伸
不可度量
2.线段、射线、直线的表示
(1)直线的表示:
C
E
m
直线m、直线CE、直线 EC
要点归纳:表示直线的方法
①用一个小写字母表示,如直线m;
②用两个大写字母表示,注:这两个大写字母可交换顺序.
(2)射线的表示:
记作: 射线 OA ( 或射线d )
O
A
d
射线用它的端点和射线上的另一点来表示 ( 表示端点的字母必须写在前面 ) 或用一个小写字母表示.
(3)线段的表示:
记作:线段 a
线段: (1) 用表示端点的两个大写字母表示;
(2) 用一个小写字母表示.
a
A
B
记作:线段 AB ( 或线段 BA )
3.两点确定一条直线
⑴ 经过一点有无数条直线;
⑵直线公理:经过两点有且只有一条直线(即:两点确定一条直线)
解释:
⑵中的“有”是存在的意思,“只有”是唯一的意思。
二、比较线段的长度
1.线段的性质
两点之间的所有连线中,线段最短.
简述为:两点之间,线段最短.
2.两点之间的距离
两点之间的距离是指连接两点的线段的长度.
3.线段长度的比较有两种方法:
(1)叠合比较法,如比较线段AB,CD的长度,可将线段
AB,CD移到同一条射线上,使它们的端点A,C都与射线的端点重合,再由点B与点D的位置关系,就可得出线段AB和CD的长度关系.
(2)度量比较法,先用刻度尺度量各线段的长度,再按照度量的长度比较它们的长短.
4.对线段的中点的认识:
(1)线段的中点是线段上的点,且把线段分成相等
的两条线段;
(2)一条线段的中点有且只有一个;
(3)如图,若M是AB的中点,则①AM=BM= AB;
②AB=2AM=2BM;③AM+BM=AB且AM=BM.反过来也成立.
A
B
M
三、角
1.角的定义
(1)角是由两条具有公共端点的射线组成的图形.
(2)角可以看做是一条射线绕着它的端点旋转而成.
2.角有两个要素:
①公共端点——角的顶点;
②两条射线——角的两边.
方法 图标 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 有弧线和数字
弧线和小写希腊字母
O
A
B
O
1
3.角的表示方法:
4.平角与周角的概念
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做平角;终边继续旋转,当它又和始边重合时,所成的角叫做周角.平角为180°,周角为360°.
5.角的度量
(1)角的度量单位是度、分、秒.
(2)它们之间的关系是六十进制的,即1°=60′,1′=60″.
四、角的比较
1. 度量法:
(1)对“中”—角的顶点对量角器的中心
(3)读数—读出角的另一边所对的度数
(2)对线—角的一边与量角器的零线重合
(1)将两个角的顶点及一边重合
(2)两个角的另一边落在重合一边的同侧
(3)由两个角的另一边的位置确定两个角的大小
2. 叠合法
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线。
⌒
⌒
2
1
O
A
C
B
注意:角平分线是一条射线.
符号语言
∵∠1=∠2 (或∠AOB= 2∠1 , ∠AOB= 2∠2)
∴射线OC平分∠AOB
∵射线OC平分∠AOB
∴∠1=∠2 (或∠AOB= 2∠1 , ∠AOB= 2∠2)
定义
性质
五、多边形的初步认识
1.多边形
(1)多边形是由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形 .
(2)连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
2.正多边形
各边相等,各角也相等的多边形叫做正多边形.
六.圆的有关概念
1.圆:
2.圆心:
平面上,一条线段绕着一个端点旋转一周,另一个端点形成的图形。
固定的端点O
3.圆弧(简称弧):
圆上任意两点A、B间的部分,读作“圆弧AB”或“弧AB”;
4.扇形:
由一条弧AB和经过这条弧的端点的两条半径OA、OB所组成的图形.
5.圆心角:
顶点在圆心的角。
考点专练
1.如右图中,共有几条线段?
2.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
6条
C
3.经过同一平面内任意三点中的两点共可以画出( )
A.一条直线 B.两条直线
C.一条或三条直线 D.三条直线
C
4.用度表示:30°45′= .
30.75°
5. 小亮利用星期天搞社会调查活动,早晨 8:00 出发,中午12:30 到家,问小亮出发时和到家时时针和分针的夹角各为______________.
120°、165°
6.如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,求MC的长。
解: ∵ AB=8 cm,BC=2 cm,
∴AC=AB-BC=6cm
又∵ M是线段AC的中点,
∴MC= AC=3cm
7.如图,直线AB、CD相交于点O,∠AOE =90°, ∠DOE =42°,则∠BOD 的度数是_____.
48°
解: ∵直线AB、CD相交于点O
∴∠AOB=180°
又∵∠AOE =90°
∴∠BOE =∠AOB-∠AOE=90°
又∵∠DOE=42°
∴∠BOD=∠BOE-∠DOE=48°
谢谢聆听
新课标 北师大版
七年级上册
单元小结
第四章
基本平面图形
本章知识架构
知识专题
一、线段、射线、直线
1.直线、射线、线段的特点:
类型
线段
射线
直线
端点数
2个
能否延伸
能否度量
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可延伸
不可度量
2.线段、射线、直线的表示
(1)直线的表示:
C
E
m
直线m、直线CE、直线 EC
要点归纳:表示直线的方法
①用一个小写字母表示,如直线m;
②用两个大写字母表示,注:这两个大写字母可交换顺序.
(2)射线的表示:
记作: 射线 OA ( 或射线d )
O
A
d
射线用它的端点和射线上的另一点来表示 ( 表示端点的字母必须写在前面 ) 或用一个小写字母表示.
(3)线段的表示:
记作:线段 a
线段: (1) 用表示端点的两个大写字母表示;
(2) 用一个小写字母表示.
a
A
B
记作:线段 AB ( 或线段 BA )
3.两点确定一条直线
⑴ 经过一点有无数条直线;
⑵直线公理:经过两点有且只有一条直线(即:两点确定一条直线)
解释:
⑵中的“有”是存在的意思,“只有”是唯一的意思。
二、比较线段的长度
1.线段的性质
两点之间的所有连线中,线段最短.
简述为:两点之间,线段最短.
2.两点之间的距离
两点之间的距离是指连接两点的线段的长度.
3.线段长度的比较有两种方法:
(1)叠合比较法,如比较线段AB,CD的长度,可将线段
AB,CD移到同一条射线上,使它们的端点A,C都与射线的端点重合,再由点B与点D的位置关系,就可得出线段AB和CD的长度关系.
(2)度量比较法,先用刻度尺度量各线段的长度,再按照度量的长度比较它们的长短.
4.对线段的中点的认识:
(1)线段的中点是线段上的点,且把线段分成相等
的两条线段;
(2)一条线段的中点有且只有一个;
(3)如图,若M是AB的中点,则①AM=BM= AB;
②AB=2AM=2BM;③AM+BM=AB且AM=BM.反过来也成立.
A
B
M
三、角
1.角的定义
(1)角是由两条具有公共端点的射线组成的图形.
(2)角可以看做是一条射线绕着它的端点旋转而成.
2.角有两个要素:
①公共端点——角的顶点;
②两条射线——角的两边.
方法 图标 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 有弧线和数字
弧线和小写希腊字母
O
A
B
O
1
3.角的表示方法:
4.平角与周角的概念
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做平角;终边继续旋转,当它又和始边重合时,所成的角叫做周角.平角为180°,周角为360°.
5.角的度量
(1)角的度量单位是度、分、秒.
(2)它们之间的关系是六十进制的,即1°=60′,1′=60″.
四、角的比较
1. 度量法:
(1)对“中”—角的顶点对量角器的中心
(3)读数—读出角的另一边所对的度数
(2)对线—角的一边与量角器的零线重合
(1)将两个角的顶点及一边重合
(2)两个角的另一边落在重合一边的同侧
(3)由两个角的另一边的位置确定两个角的大小
2. 叠合法
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线。
⌒
⌒
2
1
O
A
C
B
注意:角平分线是一条射线.
符号语言
∵∠1=∠2 (或∠AOB= 2∠1 , ∠AOB= 2∠2)
∴射线OC平分∠AOB
∵射线OC平分∠AOB
∴∠1=∠2 (或∠AOB= 2∠1 , ∠AOB= 2∠2)
定义
性质
五、多边形的初步认识
1.多边形
(1)多边形是由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形 .
(2)连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
2.正多边形
各边相等,各角也相等的多边形叫做正多边形.
六.圆的有关概念
1.圆:
2.圆心:
平面上,一条线段绕着一个端点旋转一周,另一个端点形成的图形。
固定的端点O
3.圆弧(简称弧):
圆上任意两点A、B间的部分,读作“圆弧AB”或“弧AB”;
4.扇形:
由一条弧AB和经过这条弧的端点的两条半径OA、OB所组成的图形.
5.圆心角:
顶点在圆心的角。
考点专练
1.如右图中,共有几条线段?
2.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
6条
C
3.经过同一平面内任意三点中的两点共可以画出( )
A.一条直线 B.两条直线
C.一条或三条直线 D.三条直线
C
4.用度表示:30°45′= .
30.75°
5. 小亮利用星期天搞社会调查活动,早晨 8:00 出发,中午12:30 到家,问小亮出发时和到家时时针和分针的夹角各为______________.
120°、165°
6.如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,求MC的长。
解: ∵ AB=8 cm,BC=2 cm,
∴AC=AB-BC=6cm
又∵ M是线段AC的中点,
∴MC= AC=3cm
7.如图,直线AB、CD相交于点O,∠AOE =90°, ∠DOE =42°,则∠BOD 的度数是_____.
48°
解: ∵直线AB、CD相交于点O
∴∠AOB=180°
又∵∠AOE =90°
∴∠BOE =∠AOB-∠AOE=90°
又∵∠DOE=42°
∴∠BOD=∠BOE-∠DOE=48°
谢谢聆听
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
