第四章 图形的相似(章末复习)课件(共50张PPT)-2023-2024学年九年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 第四章 图形的相似(章末复习)课件(共50张PPT)-2023-2024学年九年级数学上册同步精品课堂(北师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 22:24:22 | ||
图片预览






文档简介
(共50张PPT)
章末讲义
第四章 图形的相似
有关概念
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m,n,那么这两条线段的比就是两条线段的长度比,即AB:CD=m:n,或写成 .其中,线段AB、CD分别叫做这个线段比的前项、后项.如果把表示成比例k,则 k或AB=k CD.两条线段的比实际上就是两个数的比.
有关概念
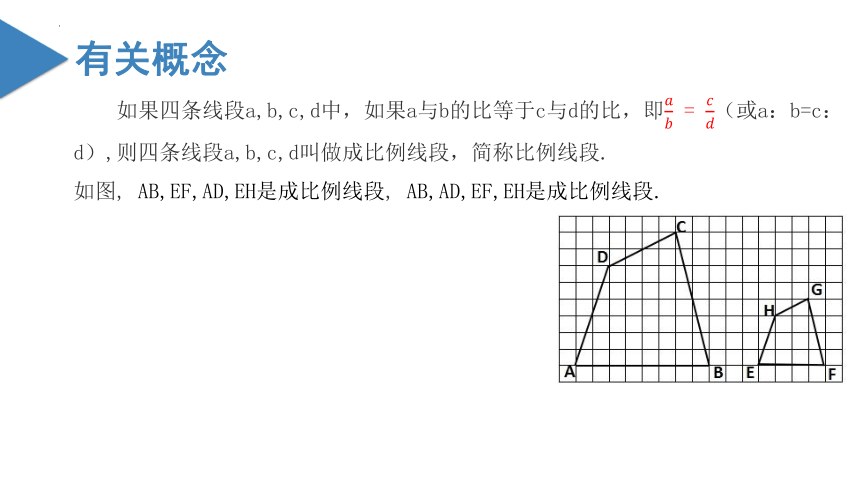
如果四条线段a,b,c,d中,如果a与b的比等于c与d的比,即 = (或a:b=c:d),则四条线段a,b,c,d叫做成比例线段,简称比例线段.
如图, AB,EF,AD,EH是成比例线段, AB,AD,EF,EH是成比例线段.
有关概念
【提问】两条线段的比和比例线段有什么区别和联系?
线段的比是指 条线段之间的比的关系,而比例线段是指 条线段间的关系.若两条线段的比 另两条线段的比,则这四条线段叫做 .
两
四
等于
成比例线段
有关概念
符号语言:
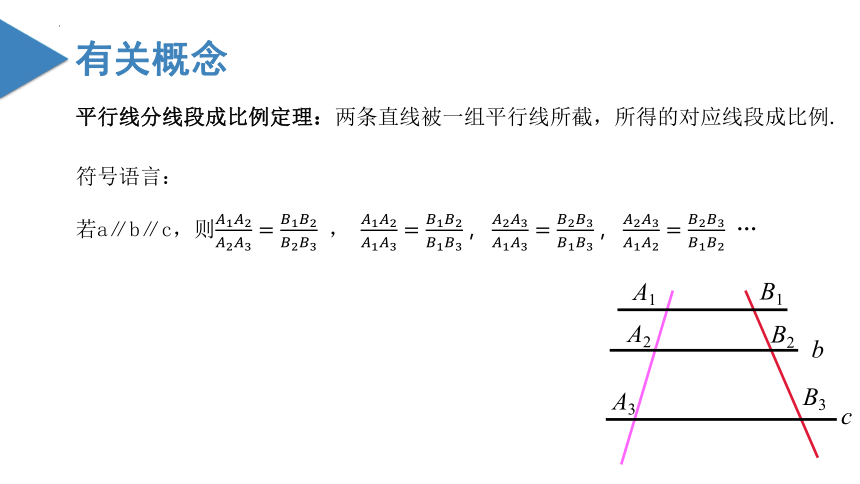
若a∥b∥c,则 , …
A1
A2
A3
B1
B2
B3
b
c
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
有关概念
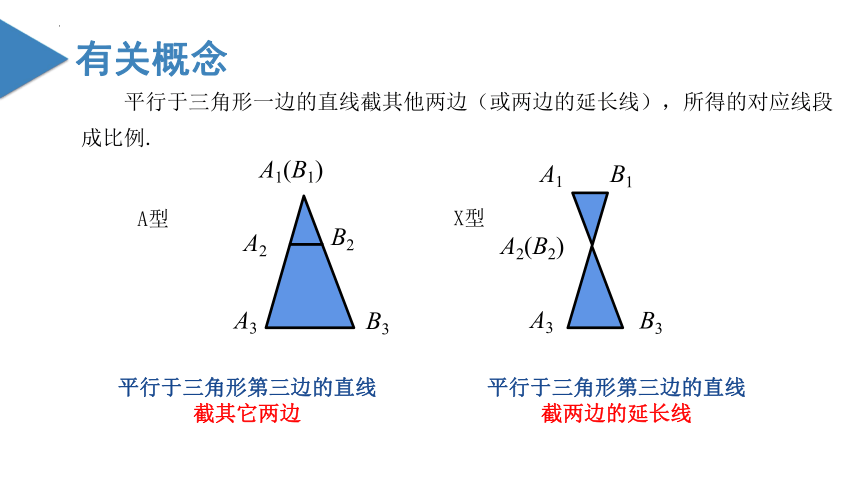
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
平行于三角形第三边的直线截其它两边
平行于三角形第三边的直线截两边的延长线
A型
X型
有关概念
生活中我们会碰到许多这样形状相同,大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
相似多边形概念:
相似多边形的特征:
如果两个边数相同的多边形对应角相等、对应边成比例的两个多边形叫做相似多边形.
相似多边形的对应角相等、对应边成比例.
相似比概念:
相似多边形对应边的比叫做相似比.
相似多边形的表示:
【注意】在记两个相似多边形时,要把表示对应顶点的字母写在对应的位置上.
相似多边形用符号“∽”表示,读作“相似于”.
有关概念
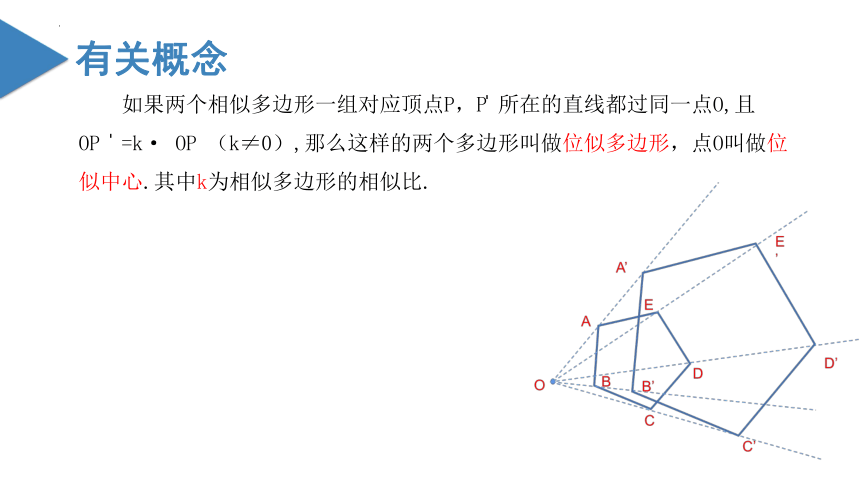
如果两个相似多边形一组对应顶点P,P 所在的直线都过同一点O,且
OP =k· OP (k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.其中k为相似多边形的相似比.
有关性质
比例的基本性质:
等比的性质:
合比的性质:
如果==…= (b+d+…+n≠0),那么=.
如果,,那么, .
有关性质
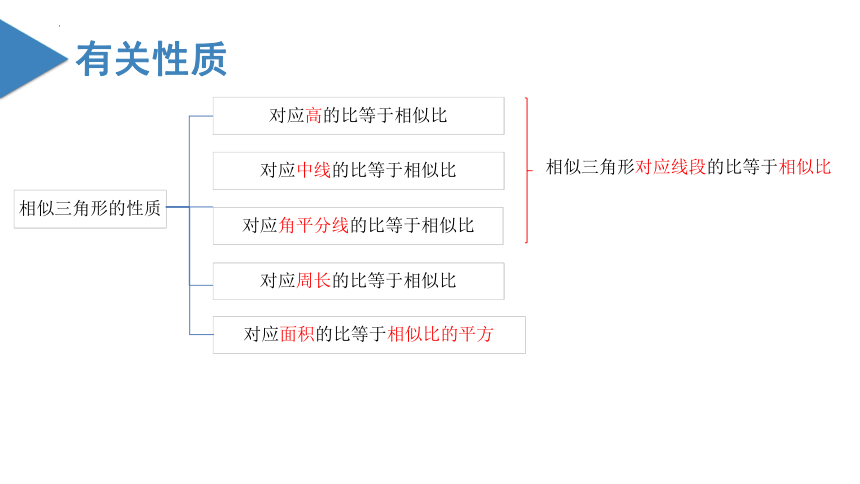
相似三角形的性质
对应高的比等于相似比
对应中线的比等于相似比
对应角平分线的比等于相似比
相似三角形对应线段的比等于相似比
对应周长的比等于相似比
对应面积的比等于相似比的平方
有关性质
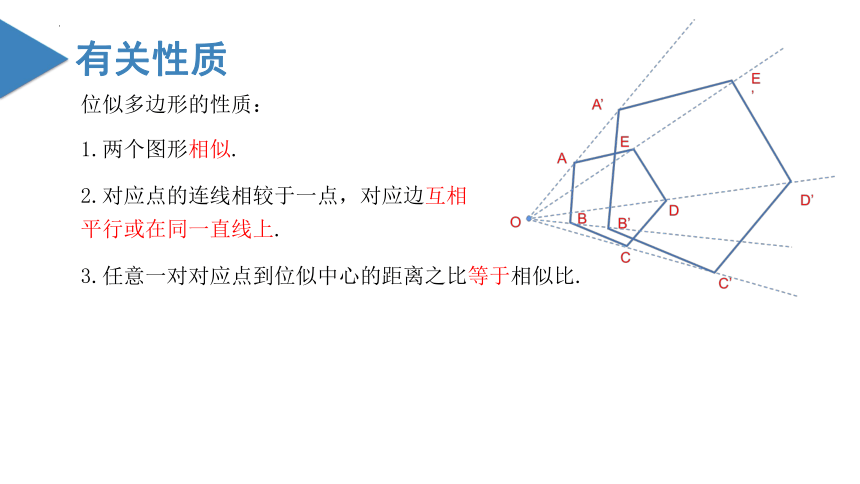
位似多边形的性质:
1.两个图形相似.
2.对应点的连线相较于一点,对应边互相
平行或在同一直线上.
3.任意一对对应点到位似中心的距离之比等于相似比.
五种方法
先将线段长度统一单位并按长度的大小排序,然后:
1)判断前两条线段的比是否与后两条线段的比相等;
2)判断最长的线段与最短的线段的乘积是否与另外两条线段的乘积相等.
【口诀】一排(排顺序)、二算(算比值或乘积)、三判(判断是否是成比例线段) .
【问题一】判断四条线段是否是成比例线段的方法?
五种方法
三角形相似判定定理1:
两角分别相等的两个三角形相似.
三角形相似判定定理2:
两边成比例且夹角相等的两个三角形相似.
三角形相似判定定理3:
三边成比例的两个三角形相似.
三角形相似判定定理4:
平行于三角形一边的直线和其他两边所构成的三角形与原三角形相似
【问题二】判断两个三角形相似的方法?
五种方法
【问题三】如何利用三角形相似求旗杆高度?
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. 即:物1高 :物2高 = 影1长 :影2长
五种方法
【问题三】如何利用三角形相似求旗杆高度?
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. 即物1高 :物2高 = 影1长 :影2长
?
D
C
五种方法
【问题三】如何利用三角形相似求旗杆高度?
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
五种方法
【问题三】如何利用三角形相似求旗杆高度?
A
E
C
N
测量不能到达顶部的物体的高度,也可以用“利用标杆测量高度”的原理解决.
五种方法
[问题四]简述位似多边形的画法?
1) 确定位似中心.
2) 确定原图形的关键点(每对对应点都在位似中心的同侧或在位似中心的异侧).
3) 确定位似比.
4) 根据对应点所在直线经过位似中心且到位似中心的距离之比等于位似比,作出关键点的对应点,再按照原图的顺序连接各点.
五种方法
[问题五]简述位似图形的坐标变换规律?
1)在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2)当位似图形在原点同侧时,相似比为 k,与它对应的点的坐标为 (kx,ky) ;
当位似图形在原点两侧时,相似比为-k,与它对应的点的坐标为 (-kx,-ky) .
3)当k>1时,图形扩大为原来的k倍;当0<k<1时,图形缩小为原来的k倍.
例1.下列四组长度的线段中,是成比例线段的是( )
A.4cm,5cm,6cm,7cm B.3cm,4cm,5cm,8cm
C.5cm,15cm,3cm,9cm D.8cm,4cm,1cm,3cm
1 下列各组线段的长度成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、8cm、6cm、12m
C.3cm、4cm、5cm、6cm D.6cm、0.3dm、8cm、0.04m
例2.若,则下列等式成立的是( )
A. B. C. D.
1.已知(a≠0,b≠0),下列变形错误的是( )
A. B.2a=3b C. D.3a=2b
2.如果,那么 .
3.若,则的值为 .
【详解】设=k,∴a+b=ck,b+c=ak,c+a=bk,
∴a+b+b+c+c+a=ck+ak+bk,即2(a+b+c)=k(a+b+c),∴(a+b+c)(2-k)=0,
当a+b+c=0时,即a+b=-c,∴k===-1,∴==k3=-1,
当a+b+c≠0时,则2-k=0,解得:k=2,∴==k3=8,
故答案为:-1或8
4.已知线段a、b、c,且.
(1)求的值;(2)若线段a、b、c满足,求a﹣b+c的值.
【详解】解:
(1)设,则a=4k,b=5k,c=6k,;
(2)设,则a=4k,b=5k,c=6k,
∵a+b+c=45,∴4k+5k+6k=45,∴k=3,
∴a=12,b=15,c=18,∴a﹣b+c=12﹣15+18=15.
例3 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
【详解】∵DE∥FG∥BC,DB=4FB,∴=3.故选B.
1.如图,直线,直线和被,,所截,,,,则的长为( )
A.2 B.3 C.4 D.
【详解】解:∵直线l1∥l2∥l3,∴.
∵AB=5,BC=6,EF=4,∴.∴DE=.故选:D.
例4 如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
E
B
F
C
解:(1)∵EF∥BC, ∴
∵AE=7,EB=5,FC=4,∴AF=
(2) ∵EF∥BC, ∴
∵AB=10,AE=6,AF=5,∴AC=
∴FC=AC-AF=
1.如图,在 中,点 是 上一点,过 作 交 于点 , BD=2 ,则 与 的比是( )
A.3:2 B.3:5 C.9:16 D.9:4
2.如图,已知AB∥CD∥EF,AC=6,CE=2,BD=4,则DF的值为( )
A. B. C. D.1
【详解】解:∵直线AB∥CD∥EF,AC=6,CE=2,BD=4,
∴ 即,解得DF=.故选:B.
【详解】解:AE//DF,,即,
,,
,,即,
,.
3.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE//AC、AE//DF,BD:AD=3:2,BF=6,求EF和FC的长.
例5 下列说法中,正确的是( )
A.所有的等腰三角形都相似 B.所有的菱形都相似
C.所有的矩形都相似 D.所有的等腰直角三角形都相似
1. 下列结论中,正确的有:( )
①所有的菱形都相似; ②放大镜下的图形与原图形不一定相似;
③等边三角形都相似; ④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
例6. 如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
1. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
2. 一个四边形的边长分别是3,4,5,6,另一个与它形状相同的四边形最短边长为6,则另一个四边形的周长是________.
36
3.已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
1)梯形ABCD与梯形A′B′C′D′的相似比k;
2)A′B′和BC的长;
3)D′C′∶DC.
【详解】
1)∵梯形ABCD∽梯形A′B′C′D′相似,∴AD:A′D′=4:6=2:3;
2)由(1)知AB: A′B′= AD:A′D′=2:3,
∵AB=6,∴A′B′=9;同理BC=8;
3)∵梯形ABCD∽梯形A′B′C′D′相似,
∴D′C′∶DC= A′D′:AD=3:2.
例7 如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC
【详解】证明:∵AD⊥AB,BE⊥AB,
∴∠DAC=90°=∠EBC,
∴∠D+∠ACD=90°,∠E+∠ECB=90°,
∵∠DCE=90°,
∴∠DCA+∠ECB=90°,
∴∠D=∠ECB,
∵∠DAC=90°=∠EBC,
∴△ACD∽△BEC.
1. 在△ABC中,D是AB上的点,且∠ACD=∠B,
1)证明:△ABC与△ACD相似.
2)AD=4,AC=6,求AB.
A
B
C
D
解:在△ABC和△ACD中
∵ ∠A=∠A,∠ACD=∠B
∴ △ABC∽△ACD
∴ = 则AB = 9
2.如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
证明:AD=1,AB=3,AC=
, 又
∽
3.如图,在中,,将沿图中的线剪开,下列四种剪开的方法中,剪下的阴影三角形与原三角形相似的是( )
A.①② B.③④ C.①③ D.①③④
【详解】②阴影部分的三角形与原三角形仅有一个角对应相等,故两三角形不一定相似;
④两三角形对应边虽然满足,但夹角不一定相等相等,故两三角形不一定相似;
故正确的有:①③,故选:C.
4.如图,在中,点为边上的一点,选择下列条件:
①;②;③;④中的一个,不能得出和相似的是: (填序号).
【详解】解:①,时,,故①不符合题意;
②,时,,故②不符合题意;
③,时,不能推出,故③符合题意;
④,时,,故④不符合题意,
故答案为:③
例8 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是( )
A.(20﹣x)2=20x B.x2=20(20﹣x)
C.x(20﹣x)=202 D.以上都不对
【详解】解:由题意知,点P是AB的黄金分割点,
且PB<PA,PB=x,则PA=20 x,∴,
∴(20 x)2=20x,故选:A.
1.已知点C在线段AB上,且满足.
(1)若AB=1,求AC的长;
(2)若AC比BC大2,求AB的长.
【详解】(1)∵点C在线段AB上,且满足,
∴点C是线段AB的黄金分割点,
∴AC= AB=,
∴AC的长为;
1.已知点C在线段AB上,且满足.
(1)若AB=1,求AC的长;
(2)若AC比BC大2,求AB的长.
【详解】(2)设AC=x,则BC=x-2,
∴AB=AC+BC=2x-2,
∵,
∴,
解得:(舍去),
∴AB=2x-2=,∴AB的长为.
例9 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,求树高AB?
【详解】∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,∴,
∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,
∴由勾股定理求得DE=40cm,∴,
∴BC=15米,∴AB=AC+BC=1.5+15=16.5(米)
答:树高AB为16.5米
1.如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(CD⊥DF,AB⊥DF,EF⊥DF),甲从点C可以看到点G处,乙从点E可以看到点D处,点B是DF的中点,墙AB高5.5米,DF=100米,BG=10.5米,求甲、乙两人的观测点到地面的距离之差(结果精确到0.1米)
【详解】解:由题意得∠ABG=∠CDG=90°,又∵∠AGD为公共角,
∴△ABG∽△CDG,∴=,
∵AB=5.5米,BG=10.5米,∴=,∴CD≈31.69(米)
又∵∠ABD=∠EFD=90°,∠EDF为公共角,∴△ADB∽△EDF,
∴==,∴EF=2AB=11(米)∴CD-EF≈20.7(米)
答:甲、乙两人的观测点到地面的距离之差约为20.7米.
2 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
【详解】∵CB⊥AD,ED⊥AD,∴∠CBA=∠EDA=90°,
∵∠CAB=∠EAD,∴ ABC∽ ADE,∴,
又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,∴,
∴AB=17,即河宽为17米.
例10 相似三角形对应边的比为1∶4,那么相似比为_________,
对应角平分线的比为______,对应高的比为_________,对应中线的比为______,
对应周长的比为__________,对应面积的比为_________.
1∶16
1∶4
1∶4
1∶4
1∶4
1∶4
1 把一个三角形变成和它相似的三角形,
1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
3)如果边长缩小到原来的一半,那么面积缩小为原来的__________。
2 若与相似且对应中线之比为,则周长之比和面积比分别是_________、____________.
25
10
3∶5
9∶25
3.已知,△ABC和△DEF中,,△ABC的周长为80厘米,求△DEF的周长.
解:,,,
∵△ABC的周长为80厘米,
∴(厘米),
答:△DEF的周长是60厘米
例11 下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点到位似中心的距离之比等于相比.其中正确的序号是( )
A.② B.①② C.③④ D.②③④
【详解】③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,但没有对应边平行(或在同一条直线上),那么这两个图形不一定位似图形,此项错误;
1.如图,以点为位似中心,将△OAB放大后得到△OCD,,则____.
2.如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若,AC=3,则DC=_____.
例12 如图,正方形OABC 与正方形ODEF是位似图,点O为位似中心,位似比为 2:3 ,点A的坐标为(0,2),则点E的坐标是 ____.
【详解】解:∵正方形OABC 与正方形ODEF是位似图,位似比为 2:3 ,
∴OA:OD=2:3,
∵点A 的坐标为(0,2),即OA=2,
∴OD=3,DE=EF=3,
故点E的坐标是(3,3).
1.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点E′的坐标为( )
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
【详解】根据题意可知,点E的对应点E′的坐标是E(﹣4,2)的坐标同时乘以2或-2,
所以点E′的坐标为(8,-4)或(-8,4).故选B.
2.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,
在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
【详解】由题意得,△ODC∽△OBA,相似比是∴
又OB=6,AB=3,∴OD=2,CD=1,∴点C的坐标为:(2,1),故选A.
章末讲义
第四章 图形的相似
有关概念
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m,n,那么这两条线段的比就是两条线段的长度比,即AB:CD=m:n,或写成 .其中,线段AB、CD分别叫做这个线段比的前项、后项.如果把表示成比例k,则 k或AB=k CD.两条线段的比实际上就是两个数的比.
有关概念
如果四条线段a,b,c,d中,如果a与b的比等于c与d的比,即 = (或a:b=c:d),则四条线段a,b,c,d叫做成比例线段,简称比例线段.
如图, AB,EF,AD,EH是成比例线段, AB,AD,EF,EH是成比例线段.
有关概念
【提问】两条线段的比和比例线段有什么区别和联系?
线段的比是指 条线段之间的比的关系,而比例线段是指 条线段间的关系.若两条线段的比 另两条线段的比,则这四条线段叫做 .
两
四
等于
成比例线段
有关概念
符号语言:
若a∥b∥c,则 , …
A1
A2
A3
B1
B2
B3
b
c
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
有关概念
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
平行于三角形第三边的直线截其它两边
平行于三角形第三边的直线截两边的延长线
A型
X型
有关概念
生活中我们会碰到许多这样形状相同,大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
相似多边形概念:
相似多边形的特征:
如果两个边数相同的多边形对应角相等、对应边成比例的两个多边形叫做相似多边形.
相似多边形的对应角相等、对应边成比例.
相似比概念:
相似多边形对应边的比叫做相似比.
相似多边形的表示:
【注意】在记两个相似多边形时,要把表示对应顶点的字母写在对应的位置上.
相似多边形用符号“∽”表示,读作“相似于”.
有关概念
如果两个相似多边形一组对应顶点P,P 所在的直线都过同一点O,且
OP =k· OP (k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.其中k为相似多边形的相似比.
有关性质
比例的基本性质:
等比的性质:
合比的性质:
如果==…= (b+d+…+n≠0),那么=.
如果,,那么, .
有关性质
相似三角形的性质
对应高的比等于相似比
对应中线的比等于相似比
对应角平分线的比等于相似比
相似三角形对应线段的比等于相似比
对应周长的比等于相似比
对应面积的比等于相似比的平方
有关性质
位似多边形的性质:
1.两个图形相似.
2.对应点的连线相较于一点,对应边互相
平行或在同一直线上.
3.任意一对对应点到位似中心的距离之比等于相似比.
五种方法
先将线段长度统一单位并按长度的大小排序,然后:
1)判断前两条线段的比是否与后两条线段的比相等;
2)判断最长的线段与最短的线段的乘积是否与另外两条线段的乘积相等.
【口诀】一排(排顺序)、二算(算比值或乘积)、三判(判断是否是成比例线段) .
【问题一】判断四条线段是否是成比例线段的方法?
五种方法
三角形相似判定定理1:
两角分别相等的两个三角形相似.
三角形相似判定定理2:
两边成比例且夹角相等的两个三角形相似.
三角形相似判定定理3:
三边成比例的两个三角形相似.
三角形相似判定定理4:
平行于三角形一边的直线和其他两边所构成的三角形与原三角形相似
【问题二】判断两个三角形相似的方法?
五种方法
【问题三】如何利用三角形相似求旗杆高度?
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. 即:物1高 :物2高 = 影1长 :影2长
五种方法
【问题三】如何利用三角形相似求旗杆高度?
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. 即物1高 :物2高 = 影1长 :影2长
?
D
C
五种方法
【问题三】如何利用三角形相似求旗杆高度?
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
五种方法
【问题三】如何利用三角形相似求旗杆高度?
A
E
C
N
测量不能到达顶部的物体的高度,也可以用“利用标杆测量高度”的原理解决.
五种方法
[问题四]简述位似多边形的画法?
1) 确定位似中心.
2) 确定原图形的关键点(每对对应点都在位似中心的同侧或在位似中心的异侧).
3) 确定位似比.
4) 根据对应点所在直线经过位似中心且到位似中心的距离之比等于位似比,作出关键点的对应点,再按照原图的顺序连接各点.
五种方法
[问题五]简述位似图形的坐标变换规律?
1)在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2)当位似图形在原点同侧时,相似比为 k,与它对应的点的坐标为 (kx,ky) ;
当位似图形在原点两侧时,相似比为-k,与它对应的点的坐标为 (-kx,-ky) .
3)当k>1时,图形扩大为原来的k倍;当0<k<1时,图形缩小为原来的k倍.
例1.下列四组长度的线段中,是成比例线段的是( )
A.4cm,5cm,6cm,7cm B.3cm,4cm,5cm,8cm
C.5cm,15cm,3cm,9cm D.8cm,4cm,1cm,3cm
1 下列各组线段的长度成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、8cm、6cm、12m
C.3cm、4cm、5cm、6cm D.6cm、0.3dm、8cm、0.04m
例2.若,则下列等式成立的是( )
A. B. C. D.
1.已知(a≠0,b≠0),下列变形错误的是( )
A. B.2a=3b C. D.3a=2b
2.如果,那么 .
3.若,则的值为 .
【详解】设=k,∴a+b=ck,b+c=ak,c+a=bk,
∴a+b+b+c+c+a=ck+ak+bk,即2(a+b+c)=k(a+b+c),∴(a+b+c)(2-k)=0,
当a+b+c=0时,即a+b=-c,∴k===-1,∴==k3=-1,
当a+b+c≠0时,则2-k=0,解得:k=2,∴==k3=8,
故答案为:-1或8
4.已知线段a、b、c,且.
(1)求的值;(2)若线段a、b、c满足,求a﹣b+c的值.
【详解】解:
(1)设,则a=4k,b=5k,c=6k,;
(2)设,则a=4k,b=5k,c=6k,
∵a+b+c=45,∴4k+5k+6k=45,∴k=3,
∴a=12,b=15,c=18,∴a﹣b+c=12﹣15+18=15.
例3 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
【详解】∵DE∥FG∥BC,DB=4FB,∴=3.故选B.
1.如图,直线,直线和被,,所截,,,,则的长为( )
A.2 B.3 C.4 D.
【详解】解:∵直线l1∥l2∥l3,∴.
∵AB=5,BC=6,EF=4,∴.∴DE=.故选:D.
例4 如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
E
B
F
C
解:(1)∵EF∥BC, ∴
∵AE=7,EB=5,FC=4,∴AF=
(2) ∵EF∥BC, ∴
∵AB=10,AE=6,AF=5,∴AC=
∴FC=AC-AF=
1.如图,在 中,点 是 上一点,过 作 交 于点 , BD=2 ,则 与 的比是( )
A.3:2 B.3:5 C.9:16 D.9:4
2.如图,已知AB∥CD∥EF,AC=6,CE=2,BD=4,则DF的值为( )
A. B. C. D.1
【详解】解:∵直线AB∥CD∥EF,AC=6,CE=2,BD=4,
∴ 即,解得DF=.故选:B.
【详解】解:AE//DF,,即,
,,
,,即,
,.
3.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE//AC、AE//DF,BD:AD=3:2,BF=6,求EF和FC的长.
例5 下列说法中,正确的是( )
A.所有的等腰三角形都相似 B.所有的菱形都相似
C.所有的矩形都相似 D.所有的等腰直角三角形都相似
1. 下列结论中,正确的有:( )
①所有的菱形都相似; ②放大镜下的图形与原图形不一定相似;
③等边三角形都相似; ④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
例6. 如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
1. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
2. 一个四边形的边长分别是3,4,5,6,另一个与它形状相同的四边形最短边长为6,则另一个四边形的周长是________.
36
3.已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
1)梯形ABCD与梯形A′B′C′D′的相似比k;
2)A′B′和BC的长;
3)D′C′∶DC.
【详解】
1)∵梯形ABCD∽梯形A′B′C′D′相似,∴AD:A′D′=4:6=2:3;
2)由(1)知AB: A′B′= AD:A′D′=2:3,
∵AB=6,∴A′B′=9;同理BC=8;
3)∵梯形ABCD∽梯形A′B′C′D′相似,
∴D′C′∶DC= A′D′:AD=3:2.
例7 如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC
【详解】证明:∵AD⊥AB,BE⊥AB,
∴∠DAC=90°=∠EBC,
∴∠D+∠ACD=90°,∠E+∠ECB=90°,
∵∠DCE=90°,
∴∠DCA+∠ECB=90°,
∴∠D=∠ECB,
∵∠DAC=90°=∠EBC,
∴△ACD∽△BEC.
1. 在△ABC中,D是AB上的点,且∠ACD=∠B,
1)证明:△ABC与△ACD相似.
2)AD=4,AC=6,求AB.
A
B
C
D
解:在△ABC和△ACD中
∵ ∠A=∠A,∠ACD=∠B
∴ △ABC∽△ACD
∴ = 则AB = 9
2.如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
证明:AD=1,AB=3,AC=
, 又
∽
3.如图,在中,,将沿图中的线剪开,下列四种剪开的方法中,剪下的阴影三角形与原三角形相似的是( )
A.①② B.③④ C.①③ D.①③④
【详解】②阴影部分的三角形与原三角形仅有一个角对应相等,故两三角形不一定相似;
④两三角形对应边虽然满足,但夹角不一定相等相等,故两三角形不一定相似;
故正确的有:①③,故选:C.
4.如图,在中,点为边上的一点,选择下列条件:
①;②;③;④中的一个,不能得出和相似的是: (填序号).
【详解】解:①,时,,故①不符合题意;
②,时,,故②不符合题意;
③,时,不能推出,故③符合题意;
④,时,,故④不符合题意,
故答案为:③
例8 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是( )
A.(20﹣x)2=20x B.x2=20(20﹣x)
C.x(20﹣x)=202 D.以上都不对
【详解】解:由题意知,点P是AB的黄金分割点,
且PB<PA,PB=x,则PA=20 x,∴,
∴(20 x)2=20x,故选:A.
1.已知点C在线段AB上,且满足.
(1)若AB=1,求AC的长;
(2)若AC比BC大2,求AB的长.
【详解】(1)∵点C在线段AB上,且满足,
∴点C是线段AB的黄金分割点,
∴AC= AB=,
∴AC的长为;
1.已知点C在线段AB上,且满足.
(1)若AB=1,求AC的长;
(2)若AC比BC大2,求AB的长.
【详解】(2)设AC=x,则BC=x-2,
∴AB=AC+BC=2x-2,
∵,
∴,
解得:(舍去),
∴AB=2x-2=,∴AB的长为.
例9 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,求树高AB?
【详解】∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,∴,
∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,
∴由勾股定理求得DE=40cm,∴,
∴BC=15米,∴AB=AC+BC=1.5+15=16.5(米)
答:树高AB为16.5米
1.如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(CD⊥DF,AB⊥DF,EF⊥DF),甲从点C可以看到点G处,乙从点E可以看到点D处,点B是DF的中点,墙AB高5.5米,DF=100米,BG=10.5米,求甲、乙两人的观测点到地面的距离之差(结果精确到0.1米)
【详解】解:由题意得∠ABG=∠CDG=90°,又∵∠AGD为公共角,
∴△ABG∽△CDG,∴=,
∵AB=5.5米,BG=10.5米,∴=,∴CD≈31.69(米)
又∵∠ABD=∠EFD=90°,∠EDF为公共角,∴△ADB∽△EDF,
∴==,∴EF=2AB=11(米)∴CD-EF≈20.7(米)
答:甲、乙两人的观测点到地面的距离之差约为20.7米.
2 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
【详解】∵CB⊥AD,ED⊥AD,∴∠CBA=∠EDA=90°,
∵∠CAB=∠EAD,∴ ABC∽ ADE,∴,
又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,∴,
∴AB=17,即河宽为17米.
例10 相似三角形对应边的比为1∶4,那么相似比为_________,
对应角平分线的比为______,对应高的比为_________,对应中线的比为______,
对应周长的比为__________,对应面积的比为_________.
1∶16
1∶4
1∶4
1∶4
1∶4
1∶4
1 把一个三角形变成和它相似的三角形,
1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
3)如果边长缩小到原来的一半,那么面积缩小为原来的__________。
2 若与相似且对应中线之比为,则周长之比和面积比分别是_________、____________.
25
10
3∶5
9∶25
3.已知,△ABC和△DEF中,,△ABC的周长为80厘米,求△DEF的周长.
解:,,,
∵△ABC的周长为80厘米,
∴(厘米),
答:△DEF的周长是60厘米
例11 下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点到位似中心的距离之比等于相比.其中正确的序号是( )
A.② B.①② C.③④ D.②③④
【详解】③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,但没有对应边平行(或在同一条直线上),那么这两个图形不一定位似图形,此项错误;
1.如图,以点为位似中心,将△OAB放大后得到△OCD,,则____.
2.如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若,AC=3,则DC=_____.
例12 如图,正方形OABC 与正方形ODEF是位似图,点O为位似中心,位似比为 2:3 ,点A的坐标为(0,2),则点E的坐标是 ____.
【详解】解:∵正方形OABC 与正方形ODEF是位似图,位似比为 2:3 ,
∴OA:OD=2:3,
∵点A 的坐标为(0,2),即OA=2,
∴OD=3,DE=EF=3,
故点E的坐标是(3,3).
1.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点E′的坐标为( )
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
【详解】根据题意可知,点E的对应点E′的坐标是E(﹣4,2)的坐标同时乘以2或-2,
所以点E′的坐标为(8,-4)或(-8,4).故选B.
2.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,
在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
【详解】由题意得,△ODC∽△OBA,相似比是∴
又OB=6,AB=3,∴OD=2,CD=1,∴点C的坐标为:(2,1),故选A.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
