2023-2024学年苏科版八年级数学上《3.1勾股定理》强化提优训练(一)(含答案)
文档属性
| 名称 | 2023-2024学年苏科版八年级数学上《3.1勾股定理》强化提优训练(一)(含答案) | 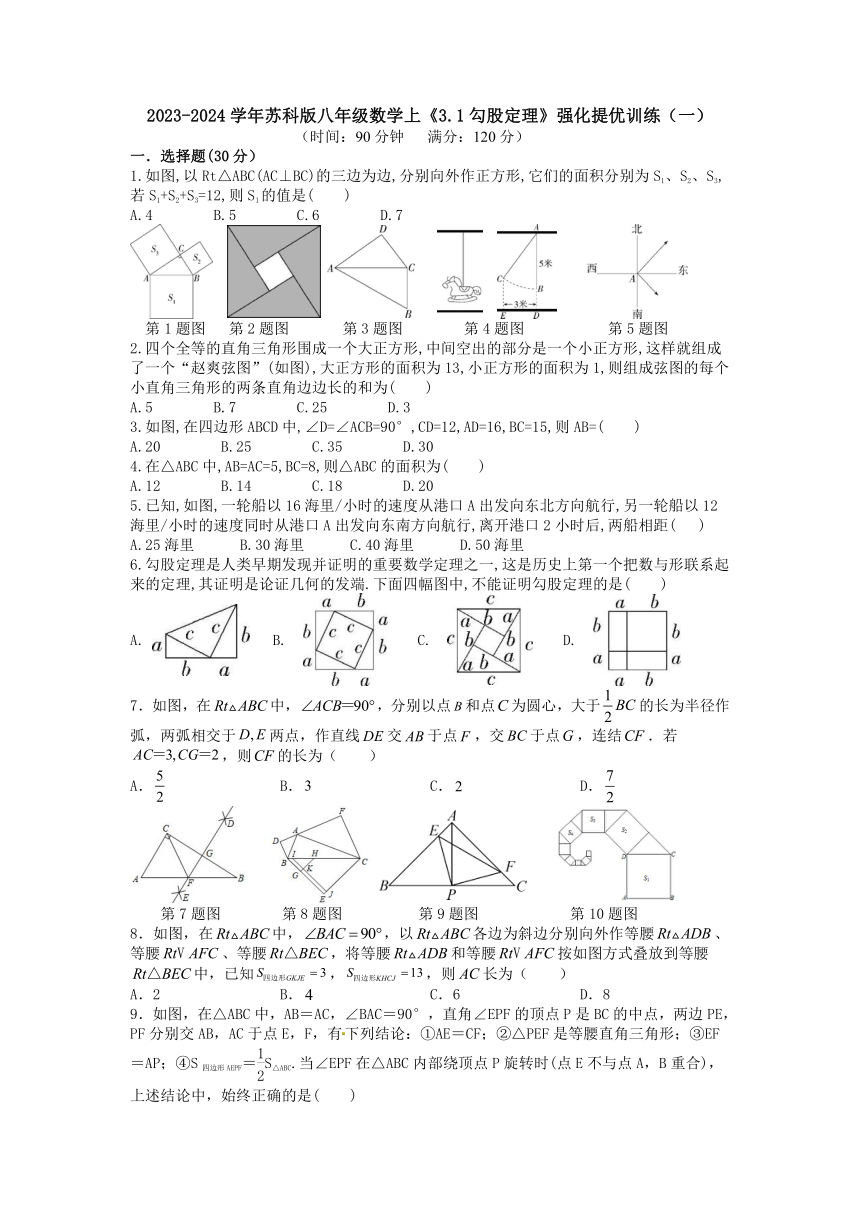 | |
| 格式 | doc | ||
| 文件大小 | 842.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 14:48:41 | ||
图片预览



文档简介
2023-2024学年苏科版八年级数学上《3.1勾股定理》强化提优训练(一)
(时间:90分钟 满分:120分)
一.选择题(30分)
1.如图,以Rt△ABC(AC⊥BC)的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=12,则S1的值是( )
A.4 B.5 C.6 D.7
第1题图 第2题图 第3题图 第4题图 第5题图
2.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两条直角边边长的和为( )
A.5 B.7 C.25 D.3
3.如图,在四边形ABCD中,∠D=∠ACB=90°,CD=12,AD=16,BC=15,则AB=( )
A.20 B.25 C.35 D.30
4.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为( )
A.12 B.14 C.18 D.20
5.已知,如图,一轮船以16海里/小时的速度从港口A出发向东北方向航行,另一轮船以12海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( )
A.25海里 B.30海里 C.40海里 D.50海里
6.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
7.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连结.若,则的长为( )
A. B. C. D.
第7题图 第8题图 第9题图 第10题图
8.如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( )
A.2 B. C.6 D.8
9.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,有下列结论:①AE=CF;②△PEF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内部绕顶点P旋转时(点E不与点A,B重合),上述结论中,始终正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①③④
10.正方形ABCD的边长为2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则s2024的值为( )
A.()2022 B.()2021 C.()2022 D.()2021
二.填空题(30分)
11.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为_______.
12.已知Rt△ABC的两边长为5和12,则其斜边上的中线长为 .
13.如图,将四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,较短直角边长为b.较长直角边长为a,已知a+b=7,ab=12,大正方形的边长为_____.
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC,∠C=90°,c=5 ,则a2+b2+c2= .
15.如图所示,已知Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于_____
16.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF的长为________________.
17.直角三角形两直角边长分别为5和12,则它斜边上的高为
18.在Rt△ABC中,∠C=90°,AC=9,AB=15,则点C到AB的距离是_______.
19、直角三角形有一条直角边为6,另两条边长是连续偶数,则该三角形周长为 .
20.在Rt△ABC中,∠C=90°,已知AC=24,AB=25,则△ABC的面积为 .
三。解答题(60分)
21.(12分)在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=5,b=12,求c.
(2)若b=0.7,c=2.5,求a.
(3)若a∶b=3∶4,c=25,求b.
22.(8分)如图,将一个长为8,宽为4的长方形纸片ABCD折叠,使C点与A点重合.
(1)求证:AE=AF;
(2)求AE的长.
23.(10分)如图,将长方形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF;
(2)若CD=4 cm,EF=5 cm,求BC的长.
24.(10分)如图,在Rt△ABC中,∠ACB=90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动时间为t s.
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
25.(10分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往点A运动,当运动到点A时停止.若设点D运动的时间为t秒,点D运动的速度为每秒1个单位长度.
(1)当t=2时,CD=________,AD=________(请直接写出答案);
(2)当△CBD是直角三角形时,t为________秒,并说明理由.
26.(12分)△ABC中AB=AC,D是射线BC上一点,过点D分别作DE⊥AB于点E,DF⊥AC于点F. (1)如图1,若D是BC边的中点,求证:DE=DF;
(2)过点B作BG⊥AC于点G.
①如图2,若D是BC边上任意一点,求证:BG=DE+DF;
②若点D是BC延长线上一点,AB=5,BC=6,DF=2,求DE的长.
图1 图2
教师样卷
一.选择题(30分)
1.如图,以Rt△ABC(AC⊥BC)的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=12,则S1的值是( D )
A.4 B.5 C.6 D.7
第1题图 第2题图 第3题图 第4题图 第5题图
2.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两条直角边边长的和为( A )
A.5 B.7 C.25 D.3
3.如图,在四边形ABCD中,∠D=∠ACB=90°,CD=12,AD=16,BC=15,则AB=( B )
A.20 B.25 C.35 D.30
4.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为( A )
A.12 B.14 C.18 D.20
5.已知,如图,一轮船以16海里/小时的速度从港口A出发向东北方向航行,另一轮船以12海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( A )
A.25海里 B.30海里 C.40海里 D.50海里
6.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( D )
A. B. C. D.
7.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连结.若,则的长为( A )
A. B. C. D.
第7题图 第8题图 第9题图 第10题图
8.如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( D )
A.2 B. C.6 D.8
9.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,有下列结论:①AE=CF;②△PEF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内部绕顶点P旋转时(点E不与点A,B重合),上述结论中,始终正确的是(B)
A. ①②③ B. ①②④ C. ②③④ D. ①③④
10.正方形ABCD的边长为2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则s2024的值为( B )
A.()2022 B.()2021 C.()2022 D.()2021
二.填空题(30分)
11.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为____12___.
12.已知Rt△ABC的两边长为5和12,则其斜边上的中线长为 6.5或6 .
13.如图,将四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,较短直角边长为b.较长直角边长为a,已知a+b=7,ab=12,大正方形的边长为__5___.
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC,∠C=90°,c=5 ,则a2+b2+c2= 50 .
15.如图所示,已知Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于_2π____
16.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF的长为_________________.
17.直角三角形两直角边长分别为5和12,则它斜边上的高为
18.在Rt△ABC中,∠C=90°,AC=9,AB=15,则点C到AB的距离是_______.
19、直角三角形有一条直角边为6,另两条边长是连续偶数,则该三角形周长为 24 .
20.在Rt△ABC中,∠C=90°,已知AC=24,AB=25,则△ABC的面积为 84 .
解:在Rt△ABC中,∠C=90°,AB=25,AC=24, ∴BC2=AB2-AC2=252-242=49,∴BC=7,
∴△ABC的面积为AC·BC=×24×7=84.
三。解答题(60分)
21.(12分)在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=5,b=12,求c.
(2)若b=0.7,c=2.5,求a.
(3)若a∶b=3∶4,c=25,求b.
解:(1)∵∠C=90°,a=5,b=12,∴c2=a2+b2=52+122=169.∵c>0,∴c=13.
(2)∵∠C=90°,b=0.7,c=2.5,∴a2=c2-b2=2.52-0.72=5.76.∵a>0,∴a=2.4.
(3)∵a∶b=3∶4,∴设a=3x,b=4x.∵∠C=90°,∴a2+b2=c2.∴(3x)2+(4x)2=252,∴x2=25.∵x>0,∴x=5,∴b=4×5=20.
22.(8分)如图,将一个长为8,宽为4的长方形纸片ABCD折叠,使C点与A点重合.
(1)求证:AE=AF; (2)求AE的长.
解:(1)证明:由折叠可知,AE=CE,∠AEF=∠CEF.又∵AD∥BC,∴∠AFE=∠FEC,
∴∠AEF=∠AFE,∴AE=AF.
(2)由折叠可知,AE=CE,∴BE=BC-CE=BC-AE=8-AE,∵∠B=90°,∴AB2+BE2=AE2,即42+(8-AE)2=AE2,∴AE=5.
23.(10分)如图,将长方形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF;
(2)若CD=4 cm,EF=5 cm,求BC的长.
解:(1)证明:∵四边形ABCD是长方形,∴AB=CD,∠A=∠B=∠ADC=∠C=90°,由折叠知,AB=PD,∠P=∠A=90°,∠PDF=∠B=90°,∴PD=CD,∠P=∠C,∠PDF=∠ADC,∴∠PDF-∠EDF=∠ADC-∠EDF,∴∠PDE=∠CDF,在△PDE和△CDF中,∴△PDE≌△CDF(ASA).
(2)如图,过点E作EG⊥BC于点G,∵四边形ABCD是长方形,∴EG=AB=CD=4 cm,又∵EF=5 cm,GF2=EF2-EG2,∴GF=3 cm,设AE=BG=x cm,则EP=x cm,∵△PDE≌△CDF,∴CF=EP=x cm,PD=CD=4 cm,∴DE=GC=GF+FC=(3+x)cm,在Rt△PED中,PE2+PD2=DE2,即x2+42=(3+x)2,解得x=,∴BC=BG+GC=(cm).
24.(10分)如图,在Rt△ABC中,∠ACB=90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动时间为t s.
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
解:在Rt△ABC中,∠ACB=90°,由勾股定理得AC2+BC2=AB2,∵AB=10 cm,AC=6 cm,∴BC2=102-62=64,∴BC=8 cm.
(1)①当∠APB=90°时,点P与点C重合,∴t=8÷1=8.
②当∠BAP=90°时,∵BP=t cm,∴CP=(t-8)cm,
在Rt△ACP中,AP2=AC2+PC2=62+(t-8)2,在Rt△BAP中,AB2+AP2=BP2,∴102+[62+(t-8)2]=t2,解得t=.综上所述,t的值为8或.
(2)当AB=AP时,BP=2BC=16 cm,则t=16÷1=16;当BA=BP=10 cm时,t=10÷1=10;当PA=PB时,如图,设BP=PA=x cm,则PC=(8-x)cm,在Rt△ACP中,由勾股定理,得PC2+AC2=AP2,即(8-x)2+62=x2,解得x=,∴t=÷1=.综上所述,t的值为16或10或.
25.(10分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往点A运动,当运动到点A时停止.若设点D运动的时间为t秒,点D运动的速度为每秒1个单位长度.
(1)当t=2时,CD=________,AD=________(请直接写出答案);
(2)当△CBD是直角三角形时,t为________秒,并说明理由.
解:(1)2 8 (2)3.6或10理由:①当∠CDB=90°时,S△ABC=AC·BD=AB·BC,
即×10·BD=×8×6,解得BD=4.8,∴CD===3.6,∴t=3.6÷1=3.6(秒);②当∠CBD=90°时,点D和点A重合,t=10÷1=10(秒).
综上所述,t为3.6秒或10秒时,△CBD是直角三角形.
26.(12分)△ABC中AB=AC,D是射线BC上一点,过点D分别作DE⊥AB于点E,DF⊥AC于点F. (1)如图1,若D是BC边的中点,求证:DE=DF;
(2)过点B作BG⊥AC于点G.
①如图2,若D是BC边上任意一点,求证:BG=DE+DF;
②若点D是BC延长线上一点,AB=5,BC=6,DF=2,求DE的长.
图1 图2
解:(1)证明:如图,连结AD.∵AB=AC,BD=CD,∴AD平分∠BAC,∵DE⊥AB,DF⊥AC,∴DE=DF.
(2)①证明:如图,连结AD.∵△ABC的面积=△ABD的面积+△ACD的面积,
∴AB·DE+AC·DF=AC·BG,∵AB=AC,∴DE+DF=BG.
②如图,连结AD,过点A作AH⊥BC于点H.∵△ABC的面积=△ABD的面积-△ACD的面积,
∴AB·DE-AC·DF=AC·BG,∵AB=AC,∴DE-DF=BG,∵AC=AB=5,BC=6,AH⊥BC,∴BH=CH=3,
∵AH2=AB2-BH2,∴AH=4,∵AC·BG=BC·AH,∴BG=,∴DE=DF+BG=2+.
(时间:90分钟 满分:120分)
一.选择题(30分)
1.如图,以Rt△ABC(AC⊥BC)的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=12,则S1的值是( )
A.4 B.5 C.6 D.7
第1题图 第2题图 第3题图 第4题图 第5题图
2.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两条直角边边长的和为( )
A.5 B.7 C.25 D.3
3.如图,在四边形ABCD中,∠D=∠ACB=90°,CD=12,AD=16,BC=15,则AB=( )
A.20 B.25 C.35 D.30
4.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为( )
A.12 B.14 C.18 D.20
5.已知,如图,一轮船以16海里/小时的速度从港口A出发向东北方向航行,另一轮船以12海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( )
A.25海里 B.30海里 C.40海里 D.50海里
6.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
7.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连结.若,则的长为( )
A. B. C. D.
第7题图 第8题图 第9题图 第10题图
8.如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( )
A.2 B. C.6 D.8
9.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,有下列结论:①AE=CF;②△PEF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内部绕顶点P旋转时(点E不与点A,B重合),上述结论中,始终正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①③④
10.正方形ABCD的边长为2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则s2024的值为( )
A.()2022 B.()2021 C.()2022 D.()2021
二.填空题(30分)
11.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为_______.
12.已知Rt△ABC的两边长为5和12,则其斜边上的中线长为 .
13.如图,将四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,较短直角边长为b.较长直角边长为a,已知a+b=7,ab=12,大正方形的边长为_____.
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC,∠C=90°,c=5 ,则a2+b2+c2= .
15.如图所示,已知Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于_____
16.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF的长为________________.
17.直角三角形两直角边长分别为5和12,则它斜边上的高为
18.在Rt△ABC中,∠C=90°,AC=9,AB=15,则点C到AB的距离是_______.
19、直角三角形有一条直角边为6,另两条边长是连续偶数,则该三角形周长为 .
20.在Rt△ABC中,∠C=90°,已知AC=24,AB=25,则△ABC的面积为 .
三。解答题(60分)
21.(12分)在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=5,b=12,求c.
(2)若b=0.7,c=2.5,求a.
(3)若a∶b=3∶4,c=25,求b.
22.(8分)如图,将一个长为8,宽为4的长方形纸片ABCD折叠,使C点与A点重合.
(1)求证:AE=AF;
(2)求AE的长.
23.(10分)如图,将长方形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF;
(2)若CD=4 cm,EF=5 cm,求BC的长.
24.(10分)如图,在Rt△ABC中,∠ACB=90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动时间为t s.
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
25.(10分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往点A运动,当运动到点A时停止.若设点D运动的时间为t秒,点D运动的速度为每秒1个单位长度.
(1)当t=2时,CD=________,AD=________(请直接写出答案);
(2)当△CBD是直角三角形时,t为________秒,并说明理由.
26.(12分)△ABC中AB=AC,D是射线BC上一点,过点D分别作DE⊥AB于点E,DF⊥AC于点F. (1)如图1,若D是BC边的中点,求证:DE=DF;
(2)过点B作BG⊥AC于点G.
①如图2,若D是BC边上任意一点,求证:BG=DE+DF;
②若点D是BC延长线上一点,AB=5,BC=6,DF=2,求DE的长.
图1 图2
教师样卷
一.选择题(30分)
1.如图,以Rt△ABC(AC⊥BC)的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=12,则S1的值是( D )
A.4 B.5 C.6 D.7
第1题图 第2题图 第3题图 第4题图 第5题图
2.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两条直角边边长的和为( A )
A.5 B.7 C.25 D.3
3.如图,在四边形ABCD中,∠D=∠ACB=90°,CD=12,AD=16,BC=15,则AB=( B )
A.20 B.25 C.35 D.30
4.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为( A )
A.12 B.14 C.18 D.20
5.已知,如图,一轮船以16海里/小时的速度从港口A出发向东北方向航行,另一轮船以12海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( A )
A.25海里 B.30海里 C.40海里 D.50海里
6.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( D )
A. B. C. D.
7.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连结.若,则的长为( A )
A. B. C. D.
第7题图 第8题图 第9题图 第10题图
8.如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( D )
A.2 B. C.6 D.8
9.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,有下列结论:①AE=CF;②△PEF是等腰直角三角形;③EF=AP;④S四边形AEPF=S△ABC.当∠EPF在△ABC内部绕顶点P旋转时(点E不与点A,B重合),上述结论中,始终正确的是(B)
A. ①②③ B. ①②④ C. ②③④ D. ①③④
10.正方形ABCD的边长为2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则s2024的值为( B )
A.()2022 B.()2021 C.()2022 D.()2021
二.填空题(30分)
11.在△ABC中,AB=AC=5,BC=8,则△ABC的面积为____12___.
12.已知Rt△ABC的两边长为5和12,则其斜边上的中线长为 6.5或6 .
13.如图,将四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,较短直角边长为b.较长直角边长为a,已知a+b=7,ab=12,大正方形的边长为__5___.
第13题图 第14题图 第15题图 第16题图
14.如图,在△ABC,∠C=90°,c=5 ,则a2+b2+c2= 50 .
15.如图所示,已知Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于_2π____
16.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF的长为_________________.
17.直角三角形两直角边长分别为5和12,则它斜边上的高为
18.在Rt△ABC中,∠C=90°,AC=9,AB=15,则点C到AB的距离是_______.
19、直角三角形有一条直角边为6,另两条边长是连续偶数,则该三角形周长为 24 .
20.在Rt△ABC中,∠C=90°,已知AC=24,AB=25,则△ABC的面积为 84 .
解:在Rt△ABC中,∠C=90°,AB=25,AC=24, ∴BC2=AB2-AC2=252-242=49,∴BC=7,
∴△ABC的面积为AC·BC=×24×7=84.
三。解答题(60分)
21.(12分)在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=5,b=12,求c.
(2)若b=0.7,c=2.5,求a.
(3)若a∶b=3∶4,c=25,求b.
解:(1)∵∠C=90°,a=5,b=12,∴c2=a2+b2=52+122=169.∵c>0,∴c=13.
(2)∵∠C=90°,b=0.7,c=2.5,∴a2=c2-b2=2.52-0.72=5.76.∵a>0,∴a=2.4.
(3)∵a∶b=3∶4,∴设a=3x,b=4x.∵∠C=90°,∴a2+b2=c2.∴(3x)2+(4x)2=252,∴x2=25.∵x>0,∴x=5,∴b=4×5=20.
22.(8分)如图,将一个长为8,宽为4的长方形纸片ABCD折叠,使C点与A点重合.
(1)求证:AE=AF; (2)求AE的长.
解:(1)证明:由折叠可知,AE=CE,∠AEF=∠CEF.又∵AD∥BC,∴∠AFE=∠FEC,
∴∠AEF=∠AFE,∴AE=AF.
(2)由折叠可知,AE=CE,∴BE=BC-CE=BC-AE=8-AE,∵∠B=90°,∴AB2+BE2=AE2,即42+(8-AE)2=AE2,∴AE=5.
23.(10分)如图,将长方形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF;
(2)若CD=4 cm,EF=5 cm,求BC的长.
解:(1)证明:∵四边形ABCD是长方形,∴AB=CD,∠A=∠B=∠ADC=∠C=90°,由折叠知,AB=PD,∠P=∠A=90°,∠PDF=∠B=90°,∴PD=CD,∠P=∠C,∠PDF=∠ADC,∴∠PDF-∠EDF=∠ADC-∠EDF,∴∠PDE=∠CDF,在△PDE和△CDF中,∴△PDE≌△CDF(ASA).
(2)如图,过点E作EG⊥BC于点G,∵四边形ABCD是长方形,∴EG=AB=CD=4 cm,又∵EF=5 cm,GF2=EF2-EG2,∴GF=3 cm,设AE=BG=x cm,则EP=x cm,∵△PDE≌△CDF,∴CF=EP=x cm,PD=CD=4 cm,∴DE=GC=GF+FC=(3+x)cm,在Rt△PED中,PE2+PD2=DE2,即x2+42=(3+x)2,解得x=,∴BC=BG+GC=(cm).
24.(10分)如图,在Rt△ABC中,∠ACB=90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动时间为t s.
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
解:在Rt△ABC中,∠ACB=90°,由勾股定理得AC2+BC2=AB2,∵AB=10 cm,AC=6 cm,∴BC2=102-62=64,∴BC=8 cm.
(1)①当∠APB=90°时,点P与点C重合,∴t=8÷1=8.
②当∠BAP=90°时,∵BP=t cm,∴CP=(t-8)cm,
在Rt△ACP中,AP2=AC2+PC2=62+(t-8)2,在Rt△BAP中,AB2+AP2=BP2,∴102+[62+(t-8)2]=t2,解得t=.综上所述,t的值为8或.
(2)当AB=AP时,BP=2BC=16 cm,则t=16÷1=16;当BA=BP=10 cm时,t=10÷1=10;当PA=PB时,如图,设BP=PA=x cm,则PC=(8-x)cm,在Rt△ACP中,由勾股定理,得PC2+AC2=AP2,即(8-x)2+62=x2,解得x=,∴t=÷1=.综上所述,t的值为16或10或.
25.(10分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往点A运动,当运动到点A时停止.若设点D运动的时间为t秒,点D运动的速度为每秒1个单位长度.
(1)当t=2时,CD=________,AD=________(请直接写出答案);
(2)当△CBD是直角三角形时,t为________秒,并说明理由.
解:(1)2 8 (2)3.6或10理由:①当∠CDB=90°时,S△ABC=AC·BD=AB·BC,
即×10·BD=×8×6,解得BD=4.8,∴CD===3.6,∴t=3.6÷1=3.6(秒);②当∠CBD=90°时,点D和点A重合,t=10÷1=10(秒).
综上所述,t为3.6秒或10秒时,△CBD是直角三角形.
26.(12分)△ABC中AB=AC,D是射线BC上一点,过点D分别作DE⊥AB于点E,DF⊥AC于点F. (1)如图1,若D是BC边的中点,求证:DE=DF;
(2)过点B作BG⊥AC于点G.
①如图2,若D是BC边上任意一点,求证:BG=DE+DF;
②若点D是BC延长线上一点,AB=5,BC=6,DF=2,求DE的长.
图1 图2
解:(1)证明:如图,连结AD.∵AB=AC,BD=CD,∴AD平分∠BAC,∵DE⊥AB,DF⊥AC,∴DE=DF.
(2)①证明:如图,连结AD.∵△ABC的面积=△ABD的面积+△ACD的面积,
∴AB·DE+AC·DF=AC·BG,∵AB=AC,∴DE+DF=BG.
②如图,连结AD,过点A作AH⊥BC于点H.∵△ABC的面积=△ABD的面积-△ACD的面积,
∴AB·DE-AC·DF=AC·BG,∵AB=AC,∴DE-DF=BG,∵AC=AB=5,BC=6,AH⊥BC,∴BH=CH=3,
∵AH2=AB2-BH2,∴AH=4,∵AC·BG=BC·AH,∴BG=,∴DE=DF+BG=2+.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
