2014—2015学年度第一学期九年级数学期末测试题
文档属性
| 名称 | 2014—2015学年度第一学期九年级数学期末测试题 |  | |
| 格式 | zip | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-09 10:30:49 | ||
图片预览


文档简介
2014—2015学年度第一学期九年级数学期末测试题
选择题(细心选一选 每题3分,共36分)
1.用配方法解方程x2+x=2,要使方程左边为x的完全平方式,应把方程两边同时
A.加 B.加 C.减 D.减
2、下列事件属于必然事件的是
A.在1个标准大气压下,水加热到100 C沸腾 B.明天我市最高气温为56 C
C.中秋节晚上能看到月亮 D.下雨后有彩虹
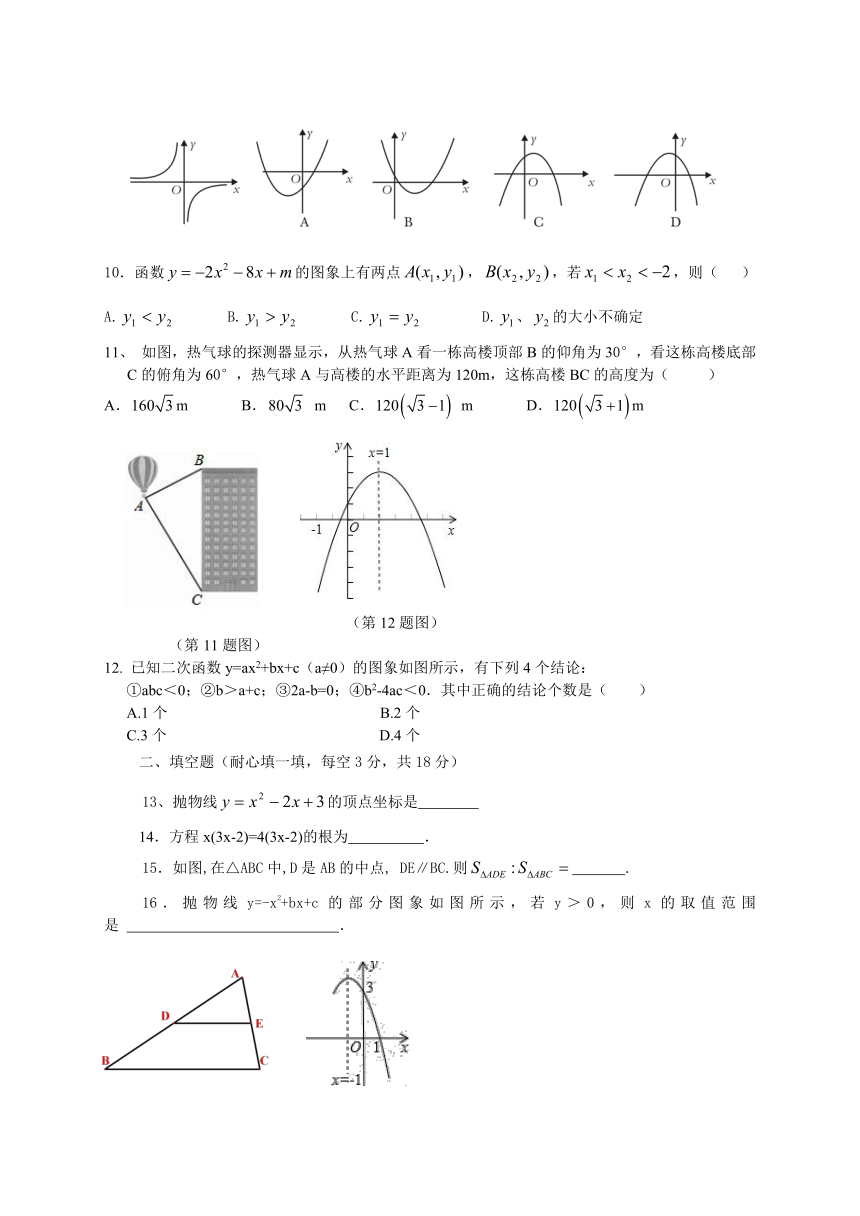
3.如图,⊙O的直径CD⊥AB,∠AOC=60°,则∠CDB=
A.20°, B.30°,C.40°,D.50°
4.学校为了解七年级学生参加课外兴趣小组 ( http: / / www.21cnjy.com )活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
A.0.1 B.0.15 C.0.25 D.0.3
(第5题图)
5. 如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )
A.1 B.2
C. D.
6. 已知反比例函数y=的图像经过点P(-1,2),则这个函数图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
7.将函数y=2x2的图象向左平移1个单位,再向上平移3个单位,可得到的抛物线是( )
A.y=2(x-1)2-3 B.y=2(x-1)2+3 C.y=2(x+1)2-3 D.y=2(x+1)2+3
8.对于抛物线-3的说法错误的是
A.抛物线的开口向下 B.抛物线的顶点坐标是(1,-3)
C.抛物线的对称轴是直线 D.当时,随的增大而增大
9. 已知反比例函数的图象如图所示,二次函数的图象大致为
( http: / / www.21cnjy.com )
10.函数的图象上有两点,,若,则( )
A. B. C. D.、的大小不确定
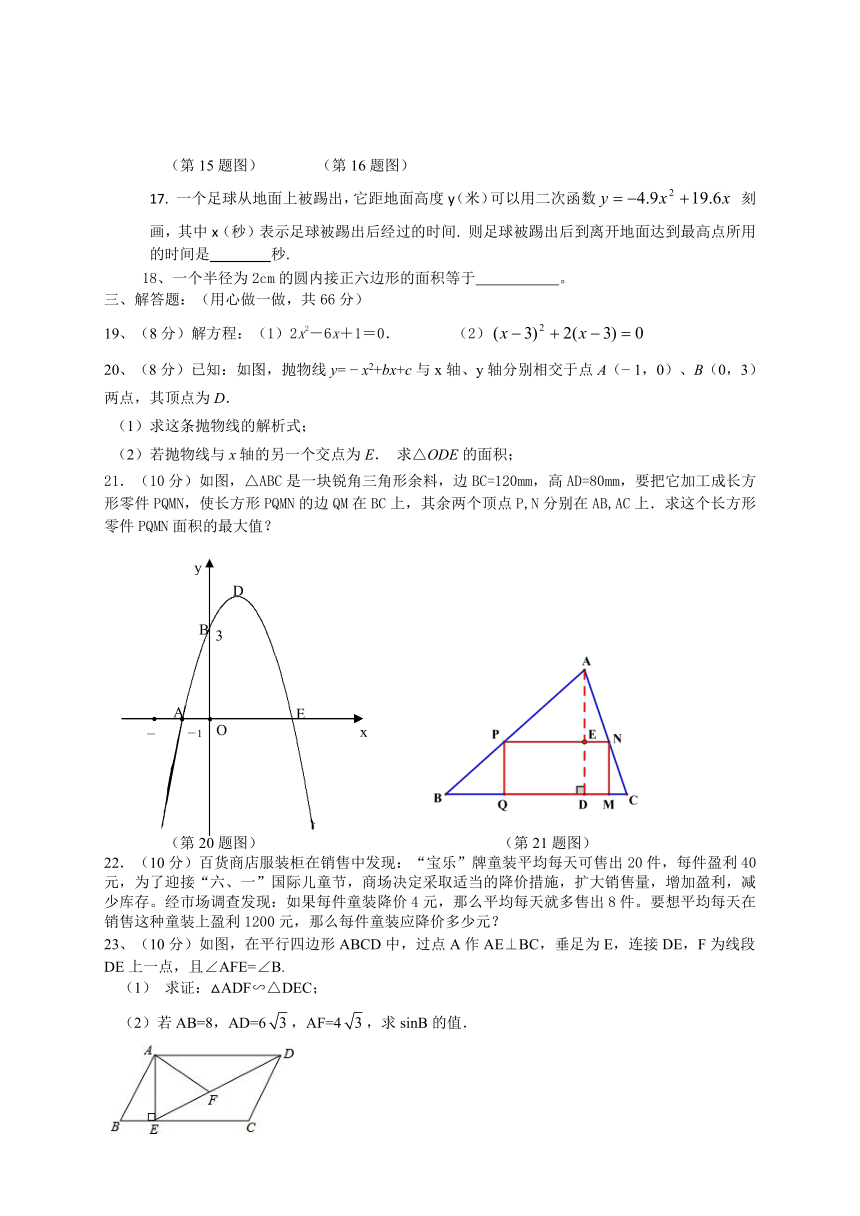
11、 如图,热气球的探测 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A.m B. m C. m D.m
(第12题图)
(第11题图)
12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc<0;②b>a+c;③2a-b=0;④b2-4ac<0.其中正确的结论个数是( )
A.1个 B.2个
C.3个 D.4个
填空题(耐心填一填,每空3分,共18分)
13、抛物线的顶点坐标是
14.方程x(3x-2)=4(3x-2)的根为 .
15.如图,在△ABC中,D是AB的中点, DE∥BC.则 .
16.抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .
(第15题图) (第16题图)
17. 一个足球从地面上被踢出,它距地面高度y(米)可以用二次函数 刻画,其中x(秒)表示足球被踢出后经过的时间. 则足球被踢出后到离开地面达到最高点所用的时间是 秒.
18、一个半径为2cm的圆内接正六边形的面积等于 。
解答题:(用心做一做,共66分)
19、(8分)解方程:(1)2x2-6x+1=0. (2)
20、(8分)已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;
21.(10分)如图,△ABC是一块锐角三 ( http: / / www.21cnjy.com )角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.求这个长方形零件PQMN面积的最大值?
(第20题图) (第21题图)
22.(10分)百货商店服装柜在销售中发现 ( http: / / www.21cnjy.com ):“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接“六、一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就多售出8件。要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
23、(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求sinB的值.
(第24题图)
(第23题图)
24、(10分)如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且
AP=AC.
(1)求证:PA是⊙O的切线; (2)若PD=,求⊙O的直径长.
25题见答案卷
学校 班级 姓名 考号
2014—2015学年度第一学期九年级数学期末测试题
答案卷
一、选择题(细心选一选 每题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(耐心填一填,每空3分,共18分)
13、 14、
15、 16、
17、 18、
三、解答题:(用心做一做,共66分)
19、(8分)解方程:(1)2x2-6x+1=0. (2)
20、(8分)已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;
(第20题图)
21.(10分)如图,△A ( http: / / www.21cnjy.com )BC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.求这个长方形零件PQMN面积的最大值?
(第21题图)
22.(10分)百货商店服装柜在销售中 ( http: / / www.21cnjy.com )发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接“六、一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就多售出8件。要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
23、(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求sinB的值.
(第23题图)
24、(10分)如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的
一点,且AP=AC.
(1)求证:PA是⊙O的切线; (2)若PD=,求⊙O的直径长.
(第24题图)
25、(10分)有一种螃蟹,从海上 ( http: / / www.21cnjy.com )捕获后不放养,最多只能存活两天.如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变,现有一经销商,按市场价收购这种活蟹1000kg放养在塘内,此时市场价为每千克30元,据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需支出各种费用为400元,且平均每天还有10kg蟹死去,假定死蟹均于当天全部销售出,售价都是每千克20元.
(1)设x天后每千克活蟹的市场价为p元,写出p关于x的函数关系式;
(2)如果放养x天后将活蟹一次性出售,所获利润为Q元,写出Q关于x的函数关系式.
(3)该经销商将这批蟹放养多少天后出售,可获最大利润,最大利润是多少?
(第3题图)
A
B
O
C
D
-1
B
D
-2
O
E
A
3
y
x
密 封 线
-1
B
D
-2
O
E
A
3
y
x
选择题(细心选一选 每题3分,共36分)
1.用配方法解方程x2+x=2,要使方程左边为x的完全平方式,应把方程两边同时
A.加 B.加 C.减 D.减
2、下列事件属于必然事件的是
A.在1个标准大气压下,水加热到100 C沸腾 B.明天我市最高气温为56 C
C.中秋节晚上能看到月亮 D.下雨后有彩虹
3.如图,⊙O的直径CD⊥AB,∠AOC=60°,则∠CDB=
A.20°, B.30°,C.40°,D.50°
4.学校为了解七年级学生参加课外兴趣小组 ( http: / / www.21cnjy.com )活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
A.0.1 B.0.15 C.0.25 D.0.3
(第5题图)
5. 如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )
A.1 B.2
C. D.
6. 已知反比例函数y=的图像经过点P(-1,2),则这个函数图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
7.将函数y=2x2的图象向左平移1个单位,再向上平移3个单位,可得到的抛物线是( )
A.y=2(x-1)2-3 B.y=2(x-1)2+3 C.y=2(x+1)2-3 D.y=2(x+1)2+3
8.对于抛物线-3的说法错误的是
A.抛物线的开口向下 B.抛物线的顶点坐标是(1,-3)
C.抛物线的对称轴是直线 D.当时,随的增大而增大
9. 已知反比例函数的图象如图所示,二次函数的图象大致为
( http: / / www.21cnjy.com )
10.函数的图象上有两点,,若,则( )
A. B. C. D.、的大小不确定
11、 如图,热气球的探测 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A.m B. m C. m D.m
(第12题图)
(第11题图)
12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc<0;②b>a+c;③2a-b=0;④b2-4ac<0.其中正确的结论个数是( )
A.1个 B.2个
C.3个 D.4个
填空题(耐心填一填,每空3分,共18分)
13、抛物线的顶点坐标是
14.方程x(3x-2)=4(3x-2)的根为 .
15.如图,在△ABC中,D是AB的中点, DE∥BC.则 .
16.抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .
(第15题图) (第16题图)
17. 一个足球从地面上被踢出,它距地面高度y(米)可以用二次函数 刻画,其中x(秒)表示足球被踢出后经过的时间. 则足球被踢出后到离开地面达到最高点所用的时间是 秒.
18、一个半径为2cm的圆内接正六边形的面积等于 。
解答题:(用心做一做,共66分)
19、(8分)解方程:(1)2x2-6x+1=0. (2)
20、(8分)已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;
21.(10分)如图,△ABC是一块锐角三 ( http: / / www.21cnjy.com )角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.求这个长方形零件PQMN面积的最大值?
(第20题图) (第21题图)
22.(10分)百货商店服装柜在销售中发现 ( http: / / www.21cnjy.com ):“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接“六、一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就多售出8件。要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
23、(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求sinB的值.
(第24题图)
(第23题图)
24、(10分)如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且
AP=AC.
(1)求证:PA是⊙O的切线; (2)若PD=,求⊙O的直径长.
25题见答案卷
学校 班级 姓名 考号
2014—2015学年度第一学期九年级数学期末测试题
答案卷
一、选择题(细心选一选 每题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(耐心填一填,每空3分,共18分)
13、 14、
15、 16、
17、 18、
三、解答题:(用心做一做,共66分)
19、(8分)解方程:(1)2x2-6x+1=0. (2)
20、(8分)已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;
(第20题图)
21.(10分)如图,△A ( http: / / www.21cnjy.com )BC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.求这个长方形零件PQMN面积的最大值?
(第21题图)
22.(10分)百货商店服装柜在销售中 ( http: / / www.21cnjy.com )发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接“六、一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就多售出8件。要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
23、(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求sinB的值.
(第23题图)
24、(10分)如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的
一点,且AP=AC.
(1)求证:PA是⊙O的切线; (2)若PD=,求⊙O的直径长.
(第24题图)
25、(10分)有一种螃蟹,从海上 ( http: / / www.21cnjy.com )捕获后不放养,最多只能存活两天.如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变,现有一经销商,按市场价收购这种活蟹1000kg放养在塘内,此时市场价为每千克30元,据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需支出各种费用为400元,且平均每天还有10kg蟹死去,假定死蟹均于当天全部销售出,售价都是每千克20元.
(1)设x天后每千克活蟹的市场价为p元,写出p关于x的函数关系式;
(2)如果放养x天后将活蟹一次性出售,所获利润为Q元,写出Q关于x的函数关系式.
(3)该经销商将这批蟹放养多少天后出售,可获最大利润,最大利润是多少?
(第3题图)
A
B
O
C
D
-1
B
D
-2
O
E
A
3
y
x
密 封 线
-1
B
D
-2
O
E
A
3
y
x
同课章节目录
