数学人教A版(2019)必修第一册1.1集合的概念(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册1.1集合的概念(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
1.1集合的含义与表示
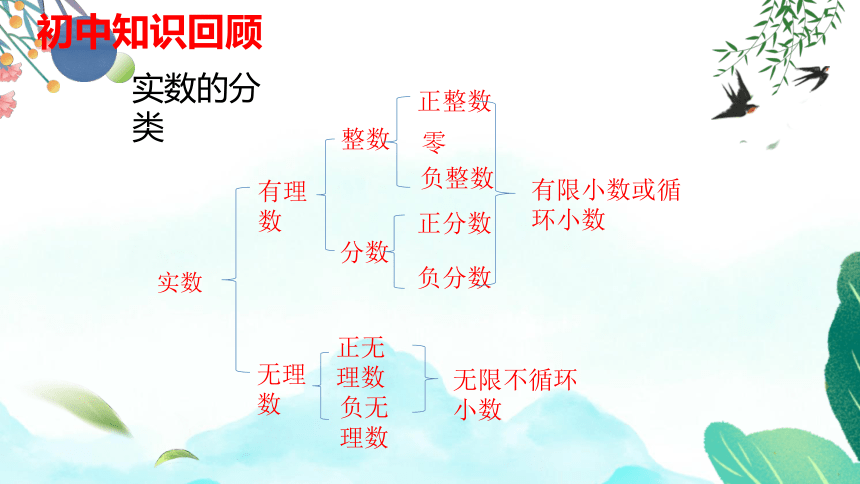
初中知识回顾
实数
零
有理数
无理数
整数
正整数
负无理数
分数
正无理数
无限不循环小数
有限小数或循环小数
负分数
负整数
正分数
实数的分类
(1)规定了原点,正方向和单位长度的直线叫数轴。
(2)数轴上的点表示数,右边的点表示的数总大于左边的点表示的数。
(3)绝对值
代数意义: =
数轴与绝对值
几何意义:在数轴上,一个数与原点的距离叫做该数的绝对值。
集合的概念
你能指出下列例子中的研究对象和研究范围吗?
(1)1~10之间的所有偶数;
(2)立德中学今年入学的全体高一学生;
(3)所有的正方形;
(4)到直线l的距离等于定长d的所有点;
(5)方程 的所有实数根;
(6)地球上的四大洋
集合的概念
元素:一般地,我们把研究对象统称为元素
集合:把一些元素组成的总体叫做集合,简称为集
思考:上述例(3)到例(6)也都能组成集合吗?它们的元素分别是什么?
所有的“帅哥”能否构成一个集合?由此说明什么?
集合中的元素是确定的
探究: 集合中元素的性质
“帅”是一个含糊不清的概念,具有相对性,多么“帅”才算“帅”?没有明确的标准,也就是说,是一些不能够确定的对象.因此,不能构成集合.
不能. 其中的元素不确定
学习新知
集合中元素的性质
由1,3,0,5,︱-3 ︳这些数组成的一个集合中有5 个 元素,这种说法正确吗?
集合中的元素是互异的
不正确.集合中只有4个不同元素1,3,0,5 .
问题探究
高一(4)班的全体同学组成一个集合,调整座位后这个集合有没有变化?
集合中的元素是没有顺序的
通过以上的学习你能给出集合中元素的特性吗?
确定性、互异性、无序性
集合没有变化
问题探究
两个集合中,元素完全一样,则称两集合相等.
练习
判断以下元素的全体是否组成集合,并说明理由:
(1) 大于3小于11的偶数; (2) 我国的小河流.
【提示】(1)是由4,6,8,10四个元素组成的集合.
(2)由集合元素的确定性知其不能组成集合.
启示:任何集合的元素都不能违背确定性、互异性、无序性.
讲授新课
已知下面的两个实例:
(1)用A表示高一(3)班全体学生组成的集合.
(2)用a表示高一(3)班的一位同学,b表示高一(4)
班的一位同学.
a是集合A中的元素,
b不是集合A中的元素.
探究 元素和集合的关系
思考:那么a,b与集合A分别有什么关系
讲授新课
元素a与集合A的关系
如果a是集合A的元素,就说a属于集合A,
记作a∈A ;
如果a不是集合A中的元素,就说a不属于集合A,
记作a A.
归纳总结
数学中常用的数集及其记法:
1.全体非负整数组成的集合称为非负整数集(或自然数集),记作;
2.全体正整数组成的集合称为正整数集,记作;
3.全体整数组成的集合称为整数集,记为;
4.全体有理数组成的集合称为有理数集,记作;
5.全体实数组成的集合称为实数集,记为.
拓展:
集合论是德国数学家康托尔于19世纪末创立的.当时,康托尔在解决涉及无限量研究的数学问题时,越过“数集”限制,提出了一般性的“集合”概念.
集合论受到许多数学家、哲学家赞誉,罗素描述其为“可能是这个时代所能夸耀的最伟大的工作”.
列举法:
把集合中的元素一一列举出来,并用花括号“{ }”括起来表示集合的方法。
深入思考
能用列举法表示不等式x-7<3的解集吗?为什么?
满足x<10的实数有无数个,无法一一列举
上述不等式的解集该如何表示?
解集中的元素都具有怎样的共同特征?
集合的表示方法
例:设不等式x-7<3的解集为A
描述法
一般地,设A是一个集合,我们把集合A中所有具有共同特征p(x)的元素x所组成的集合表示为
目标检测
例:判断以下元素的全体是否组成集合,并说明理由:
(1) 大于3小于11的偶数;
(2) 我国的小河流;
(3) 方程 的实数根;
(1) 我校2024级新生;
(2) 血压很高的人;
(3)平面直角坐标系内所有第三象限的点;
判断以下元素的全体是否组成集合,并说明理由:
变式训练:
小结:本节课有什么收获?
集合的定义
集合的特征
元素与集合的关系
常用数集的符号表示
集合的表示方法
让梦想一起飞
再见
1.1集合的含义与表示
初中知识回顾
实数
零
有理数
无理数
整数
正整数
负无理数
分数
正无理数
无限不循环小数
有限小数或循环小数
负分数
负整数
正分数
实数的分类
(1)规定了原点,正方向和单位长度的直线叫数轴。
(2)数轴上的点表示数,右边的点表示的数总大于左边的点表示的数。
(3)绝对值
代数意义: =
数轴与绝对值
几何意义:在数轴上,一个数与原点的距离叫做该数的绝对值。
集合的概念
你能指出下列例子中的研究对象和研究范围吗?
(1)1~10之间的所有偶数;
(2)立德中学今年入学的全体高一学生;
(3)所有的正方形;
(4)到直线l的距离等于定长d的所有点;
(5)方程 的所有实数根;
(6)地球上的四大洋
集合的概念
元素:一般地,我们把研究对象统称为元素
集合:把一些元素组成的总体叫做集合,简称为集
思考:上述例(3)到例(6)也都能组成集合吗?它们的元素分别是什么?
所有的“帅哥”能否构成一个集合?由此说明什么?
集合中的元素是确定的
探究: 集合中元素的性质
“帅”是一个含糊不清的概念,具有相对性,多么“帅”才算“帅”?没有明确的标准,也就是说,是一些不能够确定的对象.因此,不能构成集合.
不能. 其中的元素不确定
学习新知
集合中元素的性质
由1,3,0,5,︱-3 ︳这些数组成的一个集合中有5 个 元素,这种说法正确吗?
集合中的元素是互异的
不正确.集合中只有4个不同元素1,3,0,5 .
问题探究
高一(4)班的全体同学组成一个集合,调整座位后这个集合有没有变化?
集合中的元素是没有顺序的
通过以上的学习你能给出集合中元素的特性吗?
确定性、互异性、无序性
集合没有变化
问题探究
两个集合中,元素完全一样,则称两集合相等.
练习
判断以下元素的全体是否组成集合,并说明理由:
(1) 大于3小于11的偶数; (2) 我国的小河流.
【提示】(1)是由4,6,8,10四个元素组成的集合.
(2)由集合元素的确定性知其不能组成集合.
启示:任何集合的元素都不能违背确定性、互异性、无序性.
讲授新课
已知下面的两个实例:
(1)用A表示高一(3)班全体学生组成的集合.
(2)用a表示高一(3)班的一位同学,b表示高一(4)
班的一位同学.
a是集合A中的元素,
b不是集合A中的元素.
探究 元素和集合的关系
思考:那么a,b与集合A分别有什么关系
讲授新课
元素a与集合A的关系
如果a是集合A的元素,就说a属于集合A,
记作a∈A ;
如果a不是集合A中的元素,就说a不属于集合A,
记作a A.
归纳总结
数学中常用的数集及其记法:
1.全体非负整数组成的集合称为非负整数集(或自然数集),记作;
2.全体正整数组成的集合称为正整数集,记作;
3.全体整数组成的集合称为整数集,记为;
4.全体有理数组成的集合称为有理数集,记作;
5.全体实数组成的集合称为实数集,记为.
拓展:
集合论是德国数学家康托尔于19世纪末创立的.当时,康托尔在解决涉及无限量研究的数学问题时,越过“数集”限制,提出了一般性的“集合”概念.
集合论受到许多数学家、哲学家赞誉,罗素描述其为“可能是这个时代所能夸耀的最伟大的工作”.
列举法:
把集合中的元素一一列举出来,并用花括号“{ }”括起来表示集合的方法。
深入思考
能用列举法表示不等式x-7<3的解集吗?为什么?
满足x<10的实数有无数个,无法一一列举
上述不等式的解集该如何表示?
解集中的元素都具有怎样的共同特征?
集合的表示方法
例:设不等式x-7<3的解集为A
描述法
一般地,设A是一个集合,我们把集合A中所有具有共同特征p(x)的元素x所组成的集合表示为
目标检测
例:判断以下元素的全体是否组成集合,并说明理由:
(1) 大于3小于11的偶数;
(2) 我国的小河流;
(3) 方程 的实数根;
(1) 我校2024级新生;
(2) 血压很高的人;
(3)平面直角坐标系内所有第三象限的点;
判断以下元素的全体是否组成集合,并说明理由:
变式训练:
小结:本节课有什么收获?
集合的定义
集合的特征
元素与集合的关系
常用数集的符号表示
集合的表示方法
让梦想一起飞
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
