数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式(共21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 06:55:26 | ||
图片预览








文档简介
(共21张PPT)
2.3.3 点到直线的距离公式
2.3 直线的交点坐标与距离公式
学习目标
1. 探索并掌握推导平面上点到直线的距离公式.
2. 掌握点到直线的距离公式,能应用点到直线距离公式解决有关距离问题.
3. 通过点到直线的距离公式的探索和推导过程,培养学生运用等价转化、
数形结合等数学思想方法解决问题的能力.
在公路附近有一家乡村饭馆,现在需要铺设一条连接饭馆和公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
情景导入
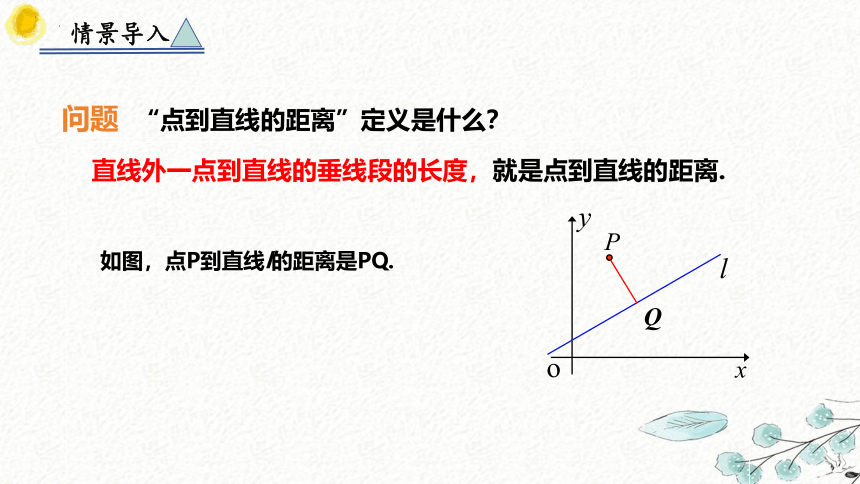
问题 “点到直线的距离”定义是什么?
直线外一点到直线的垂线段的长度,就是点到直线的距离.
如图,点P到直线l的距离是PQ.
情景导入
P
y
x
o
l
Q
问题1 如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
新知探究
P到直线 l 的距离,即垂线段|PQ|的长度
方法二:用设而不求法推导
设垂足Q的坐标为(x, y),则
问题2 我们知道,向量是解决距离、角度问题的有力工具,能否用向量方法求点到直线的距离?
x
y
O
P
Q
l
P到直线 l 的距离,即向量的模
新知探究
因为M(x, y)在直线 l 上,所以 Ax + By + C=0,
所以 Ax + By =-C
方法三:向量法
=(x-x0,y-y0),n=
问题3 除了上述两种方法,你还有其他推导方法吗?
x
y
O
P
Q
l
新知探究
如图:由直角三角形RPS的面积公式可得:
代入可得点到直线的距离公式:
当A=0或B=0时,直线方程为y=y1或x=x1的形式.
可以验证,当A=0,或B=0时,上述公式仍然成立
y
o
y=y1
(x0,y0)
x
P
x
y
o
x=x1
P(x0,y0)
点到直线的距离公式
因此,点到直线 l :Ax + By + C=0的距离
点到直线的距离公式
(1)定义:平面内点到直线的距离,等于过这个点作直线的垂线所得垂线段的长度.
(2)图示:
注意:
(1)运用此公式时要注意直线方程必须是一般式.
(2)当点P0在直线l上时,点到直线的距离为零,公式仍然适用.
点到直线的距离
(3)公式
例1(求点到直线距离) 求点P(-1,2)到直线l:3x=2的距离.
注意:直线要化为一般式!
例题讲解
例2(求直线围成图形的面积) 已知ΔABC的三个顶点A(1,3),B(3,1),C(-1,0),求ΔABC的面积.
x
y
O
A
C
B
例题讲解
例3(已知点到直线距离求参数) 已知点A(a,6)到直线3x-4y=2的距离d=4,求a的值.
例题讲解
应用点到直线的距离公式应注意的问题
(1)直线方程应为一般式,若给出其他形式,应先化成一般式再用公式.
(2)点P在直线l上时,点到直线的距离为0,公式仍然适用,故应用公式时不必判定点P与直线l的位置关系
阶段小结
1(求到两点间距离相等的直线方程) 已知点P(1,1),Q(5,4)到直线l的距离都等于2,求直线l的方程.
【分析】根据直线l与直线PQ平行,过线段PQ的中点或斜率不存在分类讨论
拓展练习
2(求点到直线的对称点) 若点A(a+2,b+2)关于直线4x+3y+11=0对称点是B(b-a,a-b),求a、b的值.
【分析】根据点关于线对称的性质,结合斜率公式、中点坐标公式进行求解即可.
拓展练习
点P(x0,y0),直线l:Ax+By+C=0
点P到直线 l 得距离为:d=
点P到直线 l 得距离|PQ|为在上的投影长度
课堂小结
THANKS
2.3.3 点到直线的距离公式
2.3 直线的交点坐标与距离公式
学习目标
1. 探索并掌握推导平面上点到直线的距离公式.
2. 掌握点到直线的距离公式,能应用点到直线距离公式解决有关距离问题.
3. 通过点到直线的距离公式的探索和推导过程,培养学生运用等价转化、
数形结合等数学思想方法解决问题的能力.
在公路附近有一家乡村饭馆,现在需要铺设一条连接饭馆和公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
情景导入
问题 “点到直线的距离”定义是什么?
直线外一点到直线的垂线段的长度,就是点到直线的距离.
如图,点P到直线l的距离是PQ.
情景导入
P
y
x
o
l
Q
问题1 如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
新知探究
P到直线 l 的距离,即垂线段|PQ|的长度
方法二:用设而不求法推导
设垂足Q的坐标为(x, y),则
问题2 我们知道,向量是解决距离、角度问题的有力工具,能否用向量方法求点到直线的距离?
x
y
O
P
Q
l
P到直线 l 的距离,即向量的模
新知探究
因为M(x, y)在直线 l 上,所以 Ax + By + C=0,
所以 Ax + By =-C
方法三:向量法
=(x-x0,y-y0),n=
问题3 除了上述两种方法,你还有其他推导方法吗?
x
y
O
P
Q
l
新知探究
如图:由直角三角形RPS的面积公式可得:
代入可得点到直线的距离公式:
当A=0或B=0时,直线方程为y=y1或x=x1的形式.
可以验证,当A=0,或B=0时,上述公式仍然成立
y
o
y=y1
(x0,y0)
x
P
x
y
o
x=x1
P(x0,y0)
点到直线的距离公式
因此,点到直线 l :Ax + By + C=0的距离
点到直线的距离公式
(1)定义:平面内点到直线的距离,等于过这个点作直线的垂线所得垂线段的长度.
(2)图示:
注意:
(1)运用此公式时要注意直线方程必须是一般式.
(2)当点P0在直线l上时,点到直线的距离为零,公式仍然适用.
点到直线的距离
(3)公式
例1(求点到直线距离) 求点P(-1,2)到直线l:3x=2的距离.
注意:直线要化为一般式!
例题讲解
例2(求直线围成图形的面积) 已知ΔABC的三个顶点A(1,3),B(3,1),C(-1,0),求ΔABC的面积.
x
y
O
A
C
B
例题讲解
例3(已知点到直线距离求参数) 已知点A(a,6)到直线3x-4y=2的距离d=4,求a的值.
例题讲解
应用点到直线的距离公式应注意的问题
(1)直线方程应为一般式,若给出其他形式,应先化成一般式再用公式.
(2)点P在直线l上时,点到直线的距离为0,公式仍然适用,故应用公式时不必判定点P与直线l的位置关系
阶段小结
1(求到两点间距离相等的直线方程) 已知点P(1,1),Q(5,4)到直线l的距离都等于2,求直线l的方程.
【分析】根据直线l与直线PQ平行,过线段PQ的中点或斜率不存在分类讨论
拓展练习
2(求点到直线的对称点) 若点A(a+2,b+2)关于直线4x+3y+11=0对称点是B(b-a,a-b),求a、b的值.
【分析】根据点关于线对称的性质,结合斜率公式、中点坐标公式进行求解即可.
拓展练习
点P(x0,y0),直线l:Ax+By+C=0
点P到直线 l 得距离为:d=
点P到直线 l 得距离|PQ|为在上的投影长度
课堂小结
THANKS
