1.1.1空间向量及其线性运算 课件(共20张PPT)
文档属性
| 名称 | 1.1.1空间向量及其线性运算 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 08:43:51 | ||
图片预览


文档简介
(共20张PPT)
1.1.1 空间向量及其线性运算
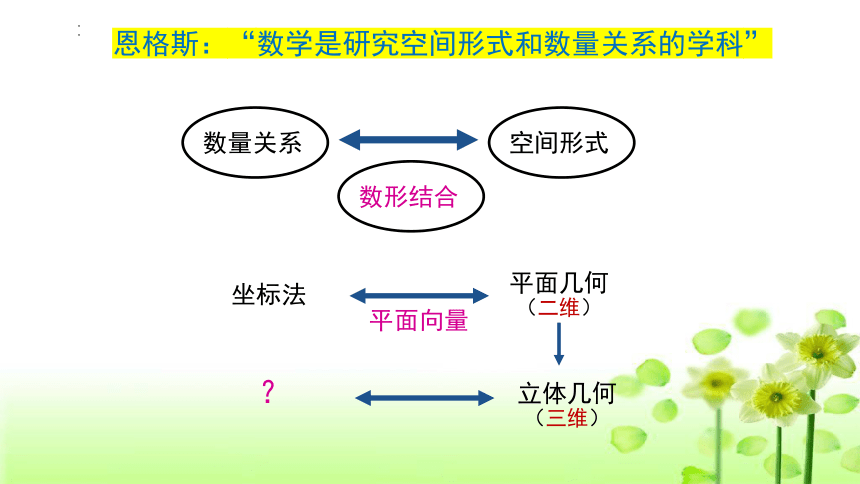
恩格斯:“数学是研究空间形式和数量关系的学科”
数量关系
空间形式
数形结合
平面几何
(二维)
立体几何
(三维)
坐标法
?
平面向量
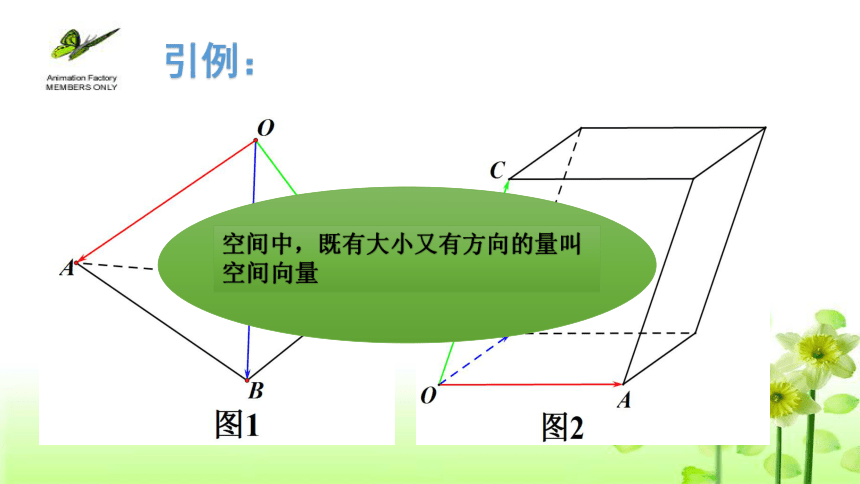
引例:
空间中,既有大小又有方向的量叫空间向量
Company Logo
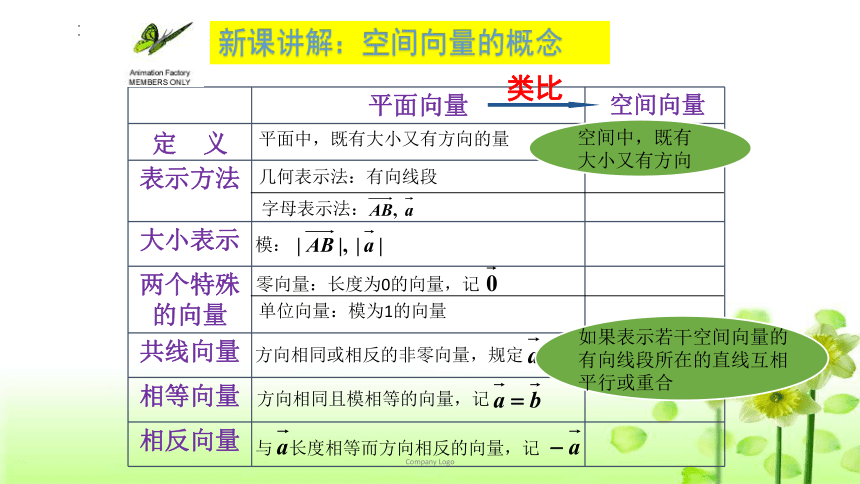
新课讲解:空间向量的概念
平面向量
定 义
表示方法
大小表示
两个特殊的向量
共线向量
相等向量
相反向量
平面中,既有大小又有方向的量
几何表示法:有向线段
字母表示法:
模:
零向量:长度为0的向量,记
单位向量:模为1的向量
方向相同且模相等的向量,记
方向相同或相反的非零向量,规定
与 长度相等而方向相反的向量,记
类比
空间向量
空间中,既有大小又有方向
如果表示若干空间向量的有向线段所在的直线互相平行或重合
例1:给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
其中不正确命题的个数是( )
A.1 B.2 C.3 D.4
C
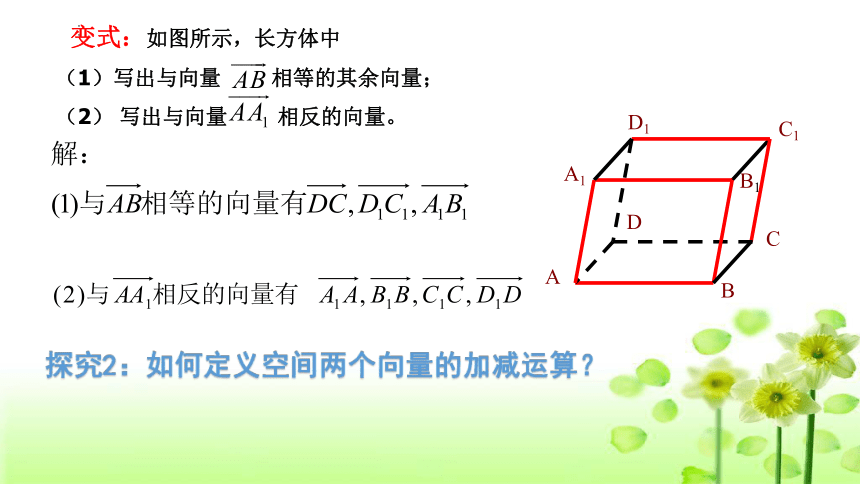
变式:如图所示,长方体中
(1)写出与向量 相等的其余向量;
(2) 写出与向量 相反的向量。
A1
D1
C1
B1
B
A
C
D
探究2:如何定义空间两个向量的加减运算?
a
b
a
b
O
A
B
b
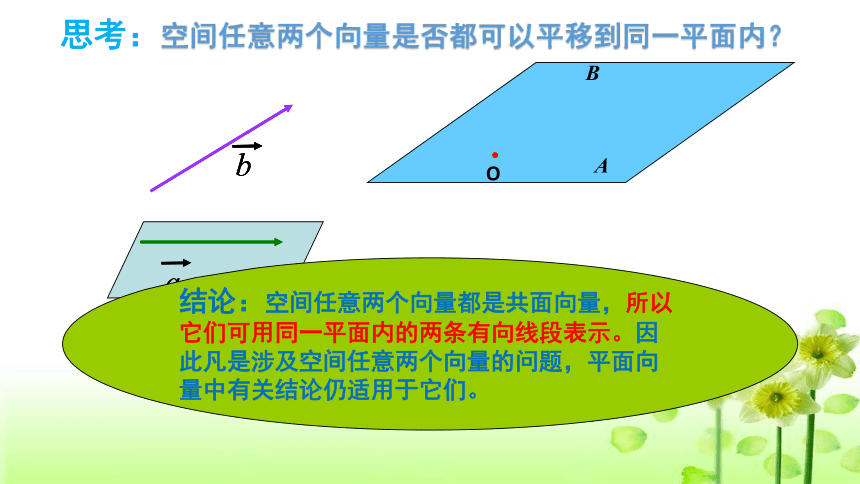
思考:空间任意两个向量是否都可以平移到同一平面内?
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示。因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。
新知讲解
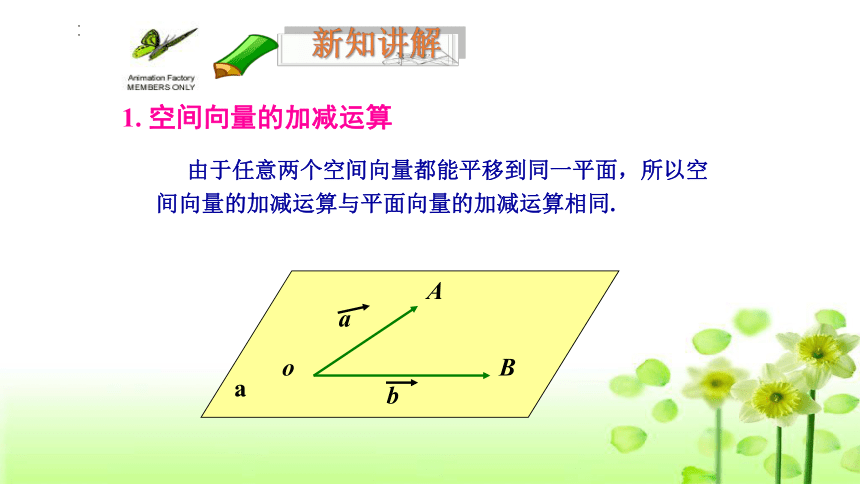
1. 空间向量的加减运算
由于任意两个空间向量都能平移到同一平面,所以空间向量的加减运算与平面向量的加减运算相同.
A
o
a
b
B
a
空间向量的加减运算
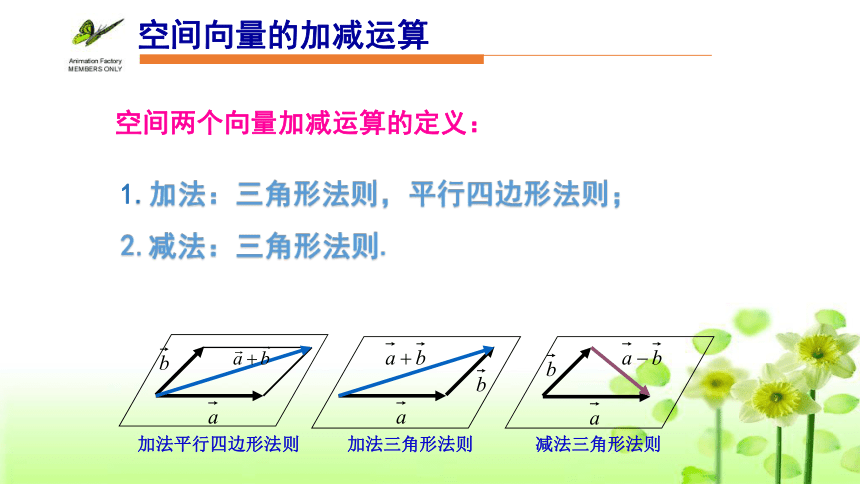
空间两个向量加减运算的定义:
加法平行四边形法则
加法三角形法则
减法三角形法则
1.加法:三角形法则,平行四边形法则;
2.减法:三角形法则.
1. 空间向量的运算就是平面向量运算的推广;
2. 两个向量相加的平行四边形法则在空间仍然成立;
3. 空间向量的加法运算可以推广至若干个向量相加.
对空间向量加减法的说明:
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
探究3:空间向量运算的运算律
追问1:平面向量线性运算的运算律有哪些?你能类比它们得出空间线性运算的运算律吗?
追问2:空间向量线性运算运算律的证明,和平面向量有哪些异同?
除空间向量加法的结合律以外,其他运算律都可以转化为平面向量线性运算的运算律进行证明.结合律涉及三个向量,它们可能不在同一个平面内
探究3:空间向量运算的运算律
追问3:如何证明空间向量的加法结合律呢?
如图,可将空间中任意三个不共面的向量,通过平移使它们起点重合,分别平移表示这三个向量的线段,构成一个平行六面体. 我们借助这个平行六面体来证明加法的结合律.
升华:如图,在平行六面体 (底面是平行四边形的四棱柱) 中,分别标出
表示的向量.
(1)从中你能体会向量加法运算的交换律和结合律吗?
(3)三个不共面的向量的和与这三个向量有什么关系?
空间向量的加减运算
(2)试用 表示向量 .
结论:三个不共面的向量的和等于以这三个向量为邻边的平行六面体的对角线所表示的向量——平行六面体法则。
空间向量的数乘运算:
2.空间向量数乘运算的性质:
(1)当
时,
与
同向
(2)当
时,
与
反向
1.定义:
实数 与空间向量 的乘积 仍然是一个向量,称为空间向量的数乘
(3)当
时,
3.空间向量数乘运算的运算律
(3)数乘结合律:
(1)数乘分配律1:
(2)数乘分配律2:
归纳反思 总结提升
1.我们学到了知识:
空间向量的概念、加减法运算、运算律
学习过程中,我们按怎样步骤研究?
2.我们体会了思想方法:
归纳类比、数形结合、化归转化
3.我们也留下了思考:
(1)空间向量的实数乘运算、数量积运算是怎么定义的?
(2)空间向量及运算能用空间坐标系表示吗?
(3)平面向量帮助我们解决平面几何问题,那空间向量呢?
作业布置
A
M
C
G
D
B
空间向量知识在中学有着非常重要的地位和教育价值,它的工具性特点在数学的许多分支中都有体现,它还为同学们以后的学习奠定了基础,能够解决高等师范院校数学专业的基础课程《高等几何》、《初等几何研究》、《空间解析几何》和《初等代数研究》中的许多问题,在解决的过程中空间向量的思想渗透的很广泛!它不仅只在数学中解决几何问题有广泛的运用,在物理学,工程科学,地理学等方面也有着广泛的应用。
在中学的学习中,空间向量在解决立体几何上的优势又是传统的知识和方法无法替代的。它可以培养我们的空间建构能力,还可以让我们体会类比的数学思想。有兴趣的同学可以下去查阅一下相关的资料。
课外延伸
反馈练习
A
D
C
相等
相反
谢谢大家!
1.1.1 空间向量及其线性运算
恩格斯:“数学是研究空间形式和数量关系的学科”
数量关系
空间形式
数形结合
平面几何
(二维)
立体几何
(三维)
坐标法
?
平面向量
引例:
空间中,既有大小又有方向的量叫空间向量
Company Logo
新课讲解:空间向量的概念
平面向量
定 义
表示方法
大小表示
两个特殊的向量
共线向量
相等向量
相反向量
平面中,既有大小又有方向的量
几何表示法:有向线段
字母表示法:
模:
零向量:长度为0的向量,记
单位向量:模为1的向量
方向相同且模相等的向量,记
方向相同或相反的非零向量,规定
与 长度相等而方向相反的向量,记
类比
空间向量
空间中,既有大小又有方向
如果表示若干空间向量的有向线段所在的直线互相平行或重合
例1:给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
其中不正确命题的个数是( )
A.1 B.2 C.3 D.4
C
变式:如图所示,长方体中
(1)写出与向量 相等的其余向量;
(2) 写出与向量 相反的向量。
A1
D1
C1
B1
B
A
C
D
探究2:如何定义空间两个向量的加减运算?
a
b
a
b
O
A
B
b
思考:空间任意两个向量是否都可以平移到同一平面内?
结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示。因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。
新知讲解
1. 空间向量的加减运算
由于任意两个空间向量都能平移到同一平面,所以空间向量的加减运算与平面向量的加减运算相同.
A
o
a
b
B
a
空间向量的加减运算
空间两个向量加减运算的定义:
加法平行四边形法则
加法三角形法则
减法三角形法则
1.加法:三角形法则,平行四边形法则;
2.减法:三角形法则.
1. 空间向量的运算就是平面向量运算的推广;
2. 两个向量相加的平行四边形法则在空间仍然成立;
3. 空间向量的加法运算可以推广至若干个向量相加.
对空间向量加减法的说明:
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
探究3:空间向量运算的运算律
追问1:平面向量线性运算的运算律有哪些?你能类比它们得出空间线性运算的运算律吗?
追问2:空间向量线性运算运算律的证明,和平面向量有哪些异同?
除空间向量加法的结合律以外,其他运算律都可以转化为平面向量线性运算的运算律进行证明.结合律涉及三个向量,它们可能不在同一个平面内
探究3:空间向量运算的运算律
追问3:如何证明空间向量的加法结合律呢?
如图,可将空间中任意三个不共面的向量,通过平移使它们起点重合,分别平移表示这三个向量的线段,构成一个平行六面体. 我们借助这个平行六面体来证明加法的结合律.
升华:如图,在平行六面体 (底面是平行四边形的四棱柱) 中,分别标出
表示的向量.
(1)从中你能体会向量加法运算的交换律和结合律吗?
(3)三个不共面的向量的和与这三个向量有什么关系?
空间向量的加减运算
(2)试用 表示向量 .
结论:三个不共面的向量的和等于以这三个向量为邻边的平行六面体的对角线所表示的向量——平行六面体法则。
空间向量的数乘运算:
2.空间向量数乘运算的性质:
(1)当
时,
与
同向
(2)当
时,
与
反向
1.定义:
实数 与空间向量 的乘积 仍然是一个向量,称为空间向量的数乘
(3)当
时,
3.空间向量数乘运算的运算律
(3)数乘结合律:
(1)数乘分配律1:
(2)数乘分配律2:
归纳反思 总结提升
1.我们学到了知识:
空间向量的概念、加减法运算、运算律
学习过程中,我们按怎样步骤研究?
2.我们体会了思想方法:
归纳类比、数形结合、化归转化
3.我们也留下了思考:
(1)空间向量的实数乘运算、数量积运算是怎么定义的?
(2)空间向量及运算能用空间坐标系表示吗?
(3)平面向量帮助我们解决平面几何问题,那空间向量呢?
作业布置
A
M
C
G
D
B
空间向量知识在中学有着非常重要的地位和教育价值,它的工具性特点在数学的许多分支中都有体现,它还为同学们以后的学习奠定了基础,能够解决高等师范院校数学专业的基础课程《高等几何》、《初等几何研究》、《空间解析几何》和《初等代数研究》中的许多问题,在解决的过程中空间向量的思想渗透的很广泛!它不仅只在数学中解决几何问题有广泛的运用,在物理学,工程科学,地理学等方面也有着广泛的应用。
在中学的学习中,空间向量在解决立体几何上的优势又是传统的知识和方法无法替代的。它可以培养我们的空间建构能力,还可以让我们体会类比的数学思想。有兴趣的同学可以下去查阅一下相关的资料。
课外延伸
反馈练习
A
D
C
相等
相反
谢谢大家!
