3.1.2点、直线与椭圆的位置关系 第2课时 课件(共17张PPT)
文档属性
| 名称 | 3.1.2点、直线与椭圆的位置关系 第2课时 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 343.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 08:43:09 | ||
图片预览




文档简介
(共17张PPT)
3.1.2 椭圆的简单几何性质
第二课时
(点、直线与椭圆的位置关系)
一、知识回顾
1.椭圆的简单几何性质:
标准方程
范围
对称性 顶点坐标
焦点坐标
半轴长 离心率 a、b、c关系 (a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
(b,0)、(-b,0)、(0,a)、(0,-a)
(0,c)、(0,-c)
关于x、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b(a>b)
-a≤x≤a,-b≤y≤b
-a≤y≤a,-b≤x≤b
a2=b2+c2(a>b>0)
2.方法归纳:
(1)将椭圆方程转化为标准方程的形式.
(2)确定焦点的位置.当焦点位置不确定时,要讨论!
(3)求椭圆的标准方程时,应:先定位(焦点),再定量(a、b)
一、知识回顾
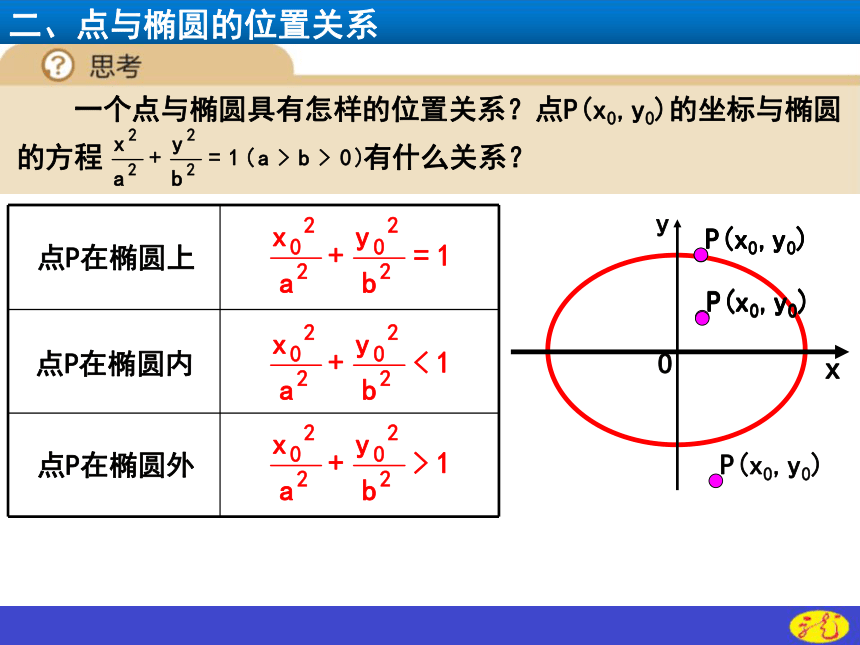
二、点与椭圆的位置关系
一个点与椭圆具有怎样的位置关系?点P(x0,y0)的坐标与椭圆的方程 有什么关系?
y
x
O
P(x0,y0)
点P在椭圆上
点P在椭圆内
点P在椭圆外
P(x0,y0)
P(x0,y0)
P(x0,y0)
P(x0,y0)
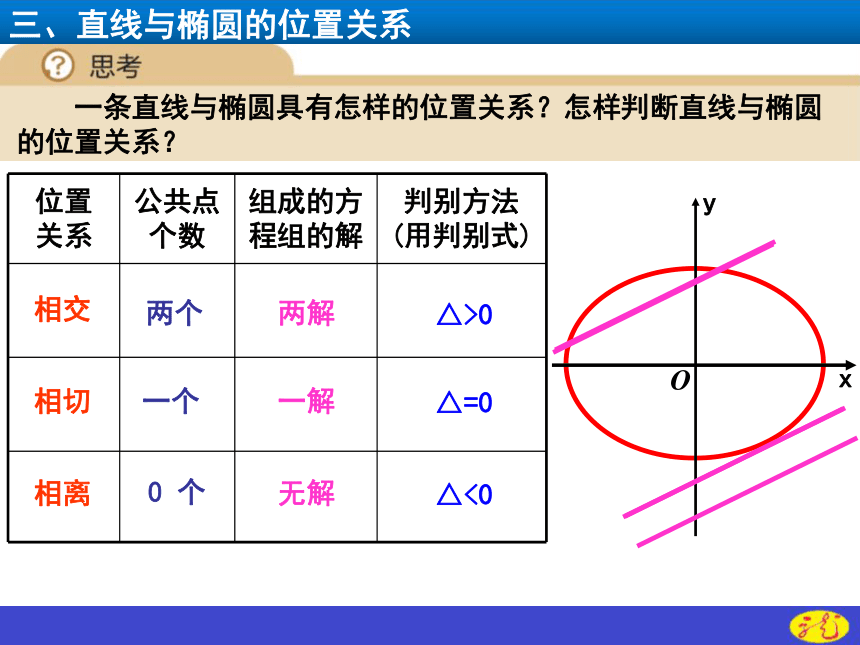
三、直线与椭圆的位置关系
一条直线与椭圆具有怎样的位置关系?怎样判断直线与椭圆的位置关系?
y
x
O
位置 关系 公共点 个数 组成的方程组的解 判别方法
(用判别式)
相交
相切
相离
两个
两解
一个
0 个
一解
无解
△>0
△=0
△<0
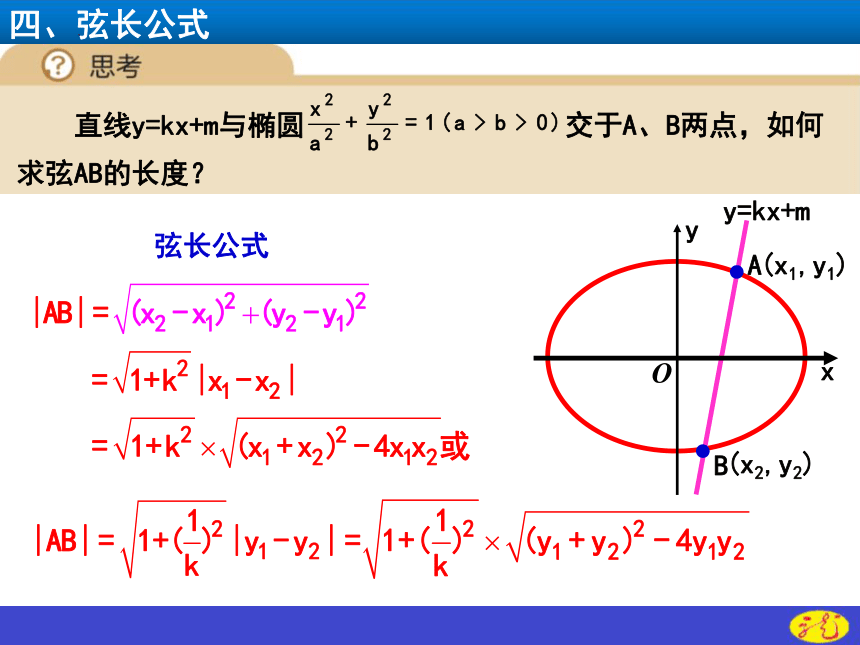
四、弦长公式
直线y=kx+m与椭圆 交于A、B两点,如何求弦AB的长度?
(x1,y1)
(x2,y2)
y
x
O
y=kx+m
B
A
弦长公式
五、典型例题
例1 如图, 已知直线l: 4x-5y+m=0和椭圆C: .
m为何值时,直线l与椭圆C: (1)有两个公共点 (2)有且只有
一个公共点 (3)没有公共点
方法归纳
五、典型例题
判断直线与椭圆的位置关系方法:
通过解直线方程与椭圆方程组成的方程组,消去y或x,得到关于x或y的一元二次方程,则:
(1)直线与椭圆相交 Δ>0;
(2)直线与椭圆相切 Δ=0;
(3)直线与椭圆相离 Δ<0.
例2 已知椭圆4x2+y2=1及直线y=x+m.
(1)当直线和椭圆有公共点时,求实数m的取值范围;
(2)求被椭圆截得的最长弦所在的直线方程.
五、典型例题
方法归纳
求弦长的方法:
(1)交点法:求出直线与椭圆的两交点坐标,用两点间的距离公式求弦长.
(2)公式法:利用弦长公式.
五、典型例题
五、典型例题
例3 已知椭圆 ,过点P(2,1)引一弦,使弦在这点被平分,
求此弦所在直线的方程.
方法归纳
解决椭圆的弦的中点问题的方法:
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用-元二次方程根与系数的关系以及中点坐标
公式解决.
(2)点差法:利用交点在曲线上,坐标满足方程,将交点坐标分别代人椭圆方程,然后作差,构造出中点坐标和斜率的关系.
五、典型例题
六、课堂小结
(1)点与椭圆的位置关系:
点P在椭圆上
点P在椭圆内
点P在椭圆外
1.知识归纳
六、课堂小结
(2)直线与椭圆的位置关系:
位置 关系 公共点 个数 组成的方程组的解 判别方法
(用判别式)
相交
相切
相离
两个
两解
一个
0 个
一解
无解
△>0
△=0
△<0
六、课堂小结
(3)弦长公式:
2.方法总结
(1)判断直线与椭圆的位置关系方法:
通过解直线方程与椭圆方程组成的方程组,消去y或x,
得到关于x或y的一元二次方程,则:
①直线与椭圆相交 Δ>0;
②直线与椭圆相切 Δ=0;
③直线与椭圆相离 Δ<0.
七、课堂小结
(2)求弦长的方法:
①交点法:求出直线与椭圆的两交点坐标,用两点间的距
离公式求弦长.
②公式法:利用弦长公式.
(3)解决椭圆的弦的中点问题的方法:
①根与系数的关系法:联立直线方程和椭圆方程构成方程组,
消去一个未知数,利用-元二次方程根
与系数的关系以及中点坐标公式解决.
②点差法:利用交点在曲线上,坐标满足方程,将交点坐标分
别代人椭圆方程,然后作差,构造出中点坐标和
斜率的关系.
五、巩固提升
课堂练习: 第112页练习第3、4题
课堂作业: 第115页习题3.1第3、4题
3.1.2 椭圆的简单几何性质
第二课时
(点、直线与椭圆的位置关系)
一、知识回顾
1.椭圆的简单几何性质:
标准方程
范围
对称性 顶点坐标
焦点坐标
半轴长 离心率 a、b、c关系 (a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
(b,0)、(-b,0)、(0,a)、(0,-a)
(0,c)、(0,-c)
关于x、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b(a>b)
-a≤x≤a,-b≤y≤b
-a≤y≤a,-b≤x≤b
a2=b2+c2(a>b>0)
2.方法归纳:
(1)将椭圆方程转化为标准方程的形式.
(2)确定焦点的位置.当焦点位置不确定时,要讨论!
(3)求椭圆的标准方程时,应:先定位(焦点),再定量(a、b)
一、知识回顾
二、点与椭圆的位置关系
一个点与椭圆具有怎样的位置关系?点P(x0,y0)的坐标与椭圆的方程 有什么关系?
y
x
O
P(x0,y0)
点P在椭圆上
点P在椭圆内
点P在椭圆外
P(x0,y0)
P(x0,y0)
P(x0,y0)
P(x0,y0)
三、直线与椭圆的位置关系
一条直线与椭圆具有怎样的位置关系?怎样判断直线与椭圆的位置关系?
y
x
O
位置 关系 公共点 个数 组成的方程组的解 判别方法
(用判别式)
相交
相切
相离
两个
两解
一个
0 个
一解
无解
△>0
△=0
△<0
四、弦长公式
直线y=kx+m与椭圆 交于A、B两点,如何求弦AB的长度?
(x1,y1)
(x2,y2)
y
x
O
y=kx+m
B
A
弦长公式
五、典型例题
例1 如图, 已知直线l: 4x-5y+m=0和椭圆C: .
m为何值时,直线l与椭圆C: (1)有两个公共点 (2)有且只有
一个公共点 (3)没有公共点
方法归纳
五、典型例题
判断直线与椭圆的位置关系方法:
通过解直线方程与椭圆方程组成的方程组,消去y或x,得到关于x或y的一元二次方程,则:
(1)直线与椭圆相交 Δ>0;
(2)直线与椭圆相切 Δ=0;
(3)直线与椭圆相离 Δ<0.
例2 已知椭圆4x2+y2=1及直线y=x+m.
(1)当直线和椭圆有公共点时,求实数m的取值范围;
(2)求被椭圆截得的最长弦所在的直线方程.
五、典型例题
方法归纳
求弦长的方法:
(1)交点法:求出直线与椭圆的两交点坐标,用两点间的距离公式求弦长.
(2)公式法:利用弦长公式.
五、典型例题
五、典型例题
例3 已知椭圆 ,过点P(2,1)引一弦,使弦在这点被平分,
求此弦所在直线的方程.
方法归纳
解决椭圆的弦的中点问题的方法:
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用-元二次方程根与系数的关系以及中点坐标
公式解决.
(2)点差法:利用交点在曲线上,坐标满足方程,将交点坐标分别代人椭圆方程,然后作差,构造出中点坐标和斜率的关系.
五、典型例题
六、课堂小结
(1)点与椭圆的位置关系:
点P在椭圆上
点P在椭圆内
点P在椭圆外
1.知识归纳
六、课堂小结
(2)直线与椭圆的位置关系:
位置 关系 公共点 个数 组成的方程组的解 判别方法
(用判别式)
相交
相切
相离
两个
两解
一个
0 个
一解
无解
△>0
△=0
△<0
六、课堂小结
(3)弦长公式:
2.方法总结
(1)判断直线与椭圆的位置关系方法:
通过解直线方程与椭圆方程组成的方程组,消去y或x,
得到关于x或y的一元二次方程,则:
①直线与椭圆相交 Δ>0;
②直线与椭圆相切 Δ=0;
③直线与椭圆相离 Δ<0.
七、课堂小结
(2)求弦长的方法:
①交点法:求出直线与椭圆的两交点坐标,用两点间的距
离公式求弦长.
②公式法:利用弦长公式.
(3)解决椭圆的弦的中点问题的方法:
①根与系数的关系法:联立直线方程和椭圆方程构成方程组,
消去一个未知数,利用-元二次方程根
与系数的关系以及中点坐标公式解决.
②点差法:利用交点在曲线上,坐标满足方程,将交点坐标分
别代人椭圆方程,然后作差,构造出中点坐标和
斜率的关系.
五、巩固提升
课堂练习: 第112页练习第3、4题
课堂作业: 第115页习题3.1第3、4题
