3.1.2椭圆的简单几何性质 课件(共23张PPT)
文档属性
| 名称 | 3.1.2椭圆的简单几何性质 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
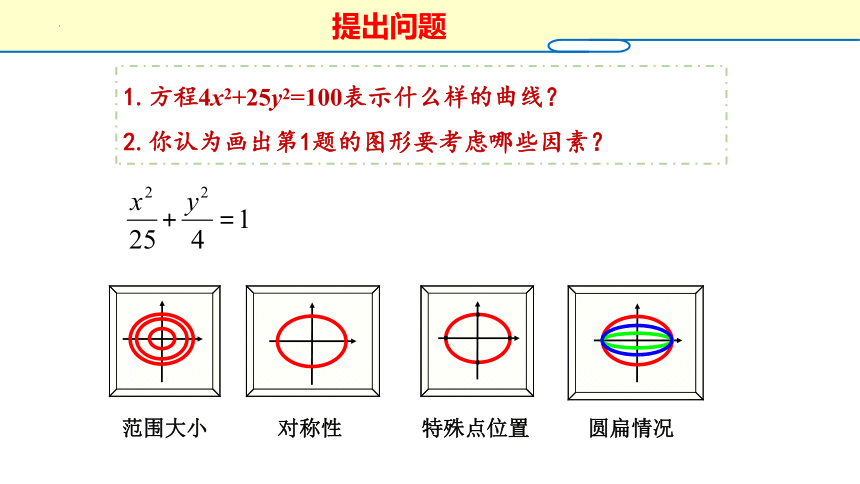
1.椭圆的定义
——————————————
2.椭圆的标准方程
焦点所在轴 焦点在x轴 焦点在y轴
图形
标准方程
焦点坐标
a,b,c的关系
x
y
o
x
y
o
a2=b2+c2
复习回顾
(±c, 0)
(0, ±c)
|MF1|+|MF2|=2a
(2a>|F1F2|)
§3.1.2 椭圆的简单几何性质
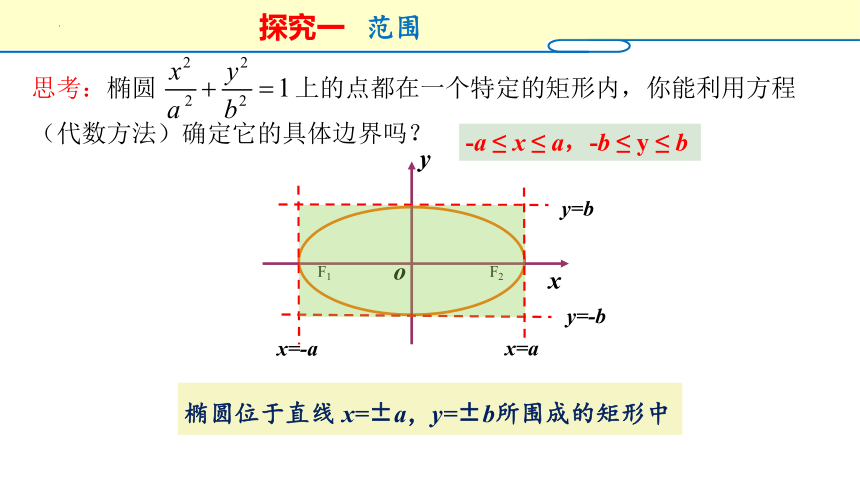
1.方程4x2+25y2=100表示什么样的曲线?
2.你认为画出第1题的图形要考虑哪些因素?
范围大小
对称性
特殊点位置
圆扁情况
提出问题
范围
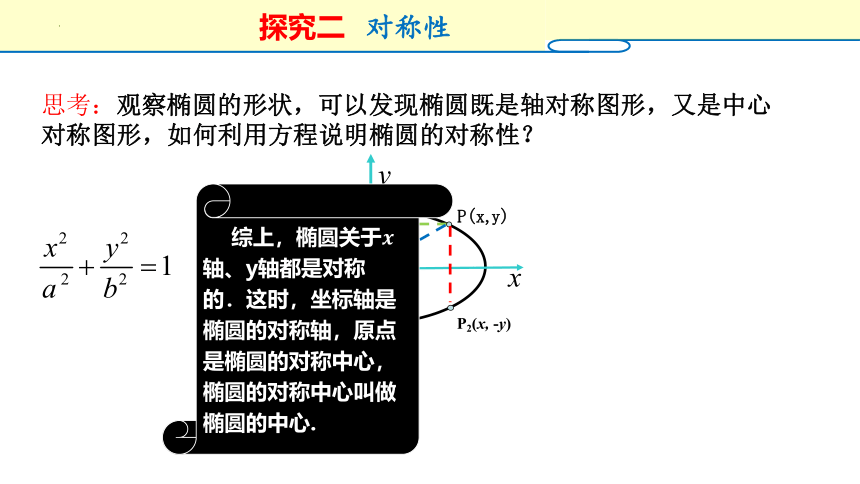
思考:椭圆 上的点都在一个特定的矩形内,你能利用方程(代数方法)确定它的具体边界吗?
o
y
F1
F2
x
y=b
y=-b
x=-a
x=a
-a ≤ x ≤ a,-b ≤ y ≤ b
椭圆位于直线 x=±a,y=±b所围成的矩形中
探究一
探究二
对称性
x
y
x
y
x
y
观察椭圆形状,它具有怎样的对称性?
关于x轴,y轴对称;关于原点中心对称
P1(-x, y)
P2(x, -y)
P3(-x, -y)
探究二
对称性
思考:观察椭圆的形状,可以发现椭圆既是轴对称图形,又是中心对称图形,如何利用方程说明椭圆的对称性?
综上,椭圆关于轴、y轴都是对称的.这时,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心叫做椭圆的中心.
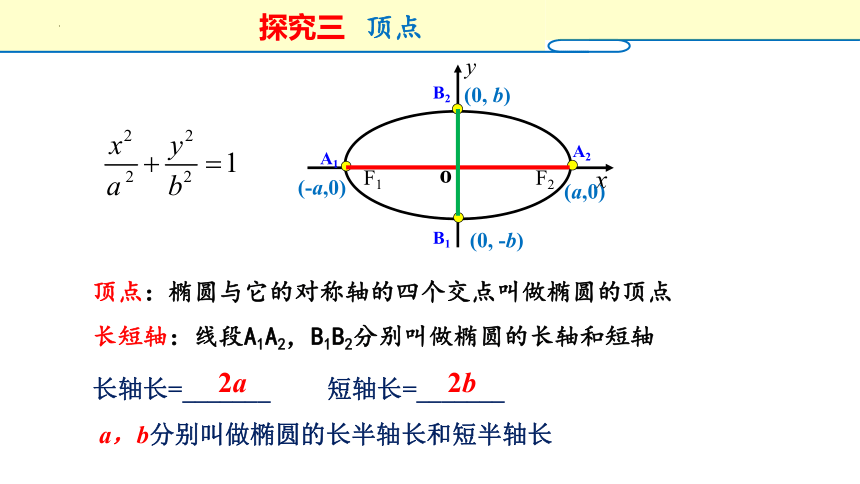
长短轴:线段A1A2,B1B2分别叫做椭圆的长轴和短轴
o
F1
F2
B2
B1
A1
A2
(-a,0)
(a,0)
(0, -b)
(0, b)
2a
a,b分别叫做椭圆的长半轴长和短半轴长
2b
探究三
顶点
顶点:椭圆与它的对称轴的四个交点叫做椭圆的顶点
长轴长=_______ 短轴长=_______
做一做
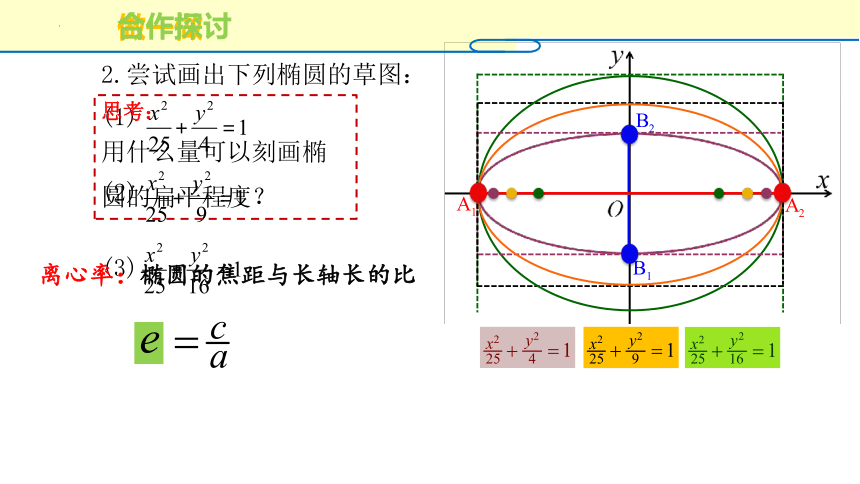
2.尝试画出下列椭圆的草图:
(1)
(2)
(3)
思考:
用什么量可以刻画椭圆的扁平程度?
合作探讨
离心率:椭圆的焦距与长轴长的比
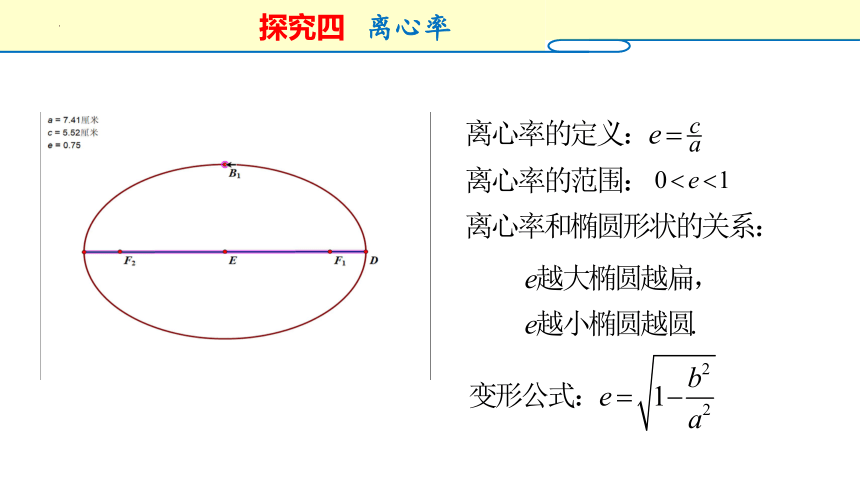
探究四
离心率
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
关于x轴、y轴成轴对称;关于原点成中心对称
(±a,0)、(0,±b)
(±c,0)
长半轴长为a,
短半轴长为b.(a>b)
(±b,0)、(0,±a)
(0 ,± c)
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,
短半轴长为b.(a>b)
-a ≤ x≤ a, - b≤ y≤ b
-a ≤ y ≤ a, - b≤ x ≤ b
a2=b2+c2
a2=b2+c2
椭圆性质
长轴长是 , 长半轴长是 ;
短轴长是 , 短半轴长是 ;
焦距是 , 离心率是 ;
焦点坐标是 , 顶点坐标是 ;
10
5
8
4
6
0.6
(±3,0 )
(0, ±4)、(±5, 0)
2.已知椭圆 16x2 + 25y2 =400,则:
1、椭圆 的离心率为( )
A. B. C. D.
D
B2
o
F1
F2
B1
A1
A2
例题巩固
例1
例2 根据下列条件求椭圆的标准方程:
(1)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
例题巩固
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
例题巩固
例题巩固
例题巩固
解:在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,
例题巩固
例题巩固
√
解析 设左焦点为F0,连接F0A,F0B,则四边形AFBF0为平行四边形.
∵|AF|+|BF|=4,∴|AF|+|AF0|=4,
∴a=2.
故选A.
例题巩固
例3
典例分析
范围、对称性、顶点、离心率
(a>0,b>0)
例4: 如图所示,椭圆的中心在原点,焦点F1,F2在x轴上,A,B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2 // AB,求此椭圆的离心率:
P
A
B
F2
F1
O
(1)4个基本量:
(2)7个基本点:
(3)2条基本线:
几何意义:
相互关系:
a长半轴, b短半轴, c半焦距,e离心率;
e
顶点、中心
对称轴
范围、对称性、顶点、离心率
(a>0,b>0)
椭圆的基本要素:
焦点、
a、b、c、
课堂小结
1.椭圆的定义
——————————————
2.椭圆的标准方程
焦点所在轴 焦点在x轴 焦点在y轴
图形
标准方程
焦点坐标
a,b,c的关系
x
y
o
x
y
o
a2=b2+c2
复习回顾
(±c, 0)
(0, ±c)
|MF1|+|MF2|=2a
(2a>|F1F2|)
§3.1.2 椭圆的简单几何性质
1.方程4x2+25y2=100表示什么样的曲线?
2.你认为画出第1题的图形要考虑哪些因素?
范围大小
对称性
特殊点位置
圆扁情况
提出问题
范围
思考:椭圆 上的点都在一个特定的矩形内,你能利用方程(代数方法)确定它的具体边界吗?
o
y
F1
F2
x
y=b
y=-b
x=-a
x=a
-a ≤ x ≤ a,-b ≤ y ≤ b
椭圆位于直线 x=±a,y=±b所围成的矩形中
探究一
探究二
对称性
x
y
x
y
x
y
观察椭圆形状,它具有怎样的对称性?
关于x轴,y轴对称;关于原点中心对称
P1(-x, y)
P2(x, -y)
P3(-x, -y)
探究二
对称性
思考:观察椭圆的形状,可以发现椭圆既是轴对称图形,又是中心对称图形,如何利用方程说明椭圆的对称性?
综上,椭圆关于轴、y轴都是对称的.这时,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心叫做椭圆的中心.
长短轴:线段A1A2,B1B2分别叫做椭圆的长轴和短轴
o
F1
F2
B2
B1
A1
A2
(-a,0)
(a,0)
(0, -b)
(0, b)
2a
a,b分别叫做椭圆的长半轴长和短半轴长
2b
探究三
顶点
顶点:椭圆与它的对称轴的四个交点叫做椭圆的顶点
长轴长=_______ 短轴长=_______
做一做
2.尝试画出下列椭圆的草图:
(1)
(2)
(3)
思考:
用什么量可以刻画椭圆的扁平程度?
合作探讨
离心率:椭圆的焦距与长轴长的比
探究四
离心率
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
关于x轴、y轴成轴对称;关于原点成中心对称
(±a,0)、(0,±b)
(±c,0)
长半轴长为a,
短半轴长为b.(a>b)
(±b,0)、(0,±a)
(0 ,± c)
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,
短半轴长为b.(a>b)
-a ≤ x≤ a, - b≤ y≤ b
-a ≤ y ≤ a, - b≤ x ≤ b
a2=b2+c2
a2=b2+c2
椭圆性质
长轴长是 , 长半轴长是 ;
短轴长是 , 短半轴长是 ;
焦距是 , 离心率是 ;
焦点坐标是 , 顶点坐标是 ;
10
5
8
4
6
0.6
(±3,0 )
(0, ±4)、(±5, 0)
2.已知椭圆 16x2 + 25y2 =400,则:
1、椭圆 的离心率为( )
A. B. C. D.
D
B2
o
F1
F2
B1
A1
A2
例题巩固
例1
例2 根据下列条件求椭圆的标准方程:
(1)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
例题巩固
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
例题巩固
例题巩固
例题巩固
解:在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,
例题巩固
例题巩固
√
解析 设左焦点为F0,连接F0A,F0B,则四边形AFBF0为平行四边形.
∵|AF|+|BF|=4,∴|AF|+|AF0|=4,
∴a=2.
故选A.
例题巩固
例3
典例分析
范围、对称性、顶点、离心率
(a>0,b>0)
例4: 如图所示,椭圆的中心在原点,焦点F1,F2在x轴上,A,B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2 // AB,求此椭圆的离心率:
P
A
B
F2
F1
O
(1)4个基本量:
(2)7个基本点:
(3)2条基本线:
几何意义:
相互关系:
a长半轴, b短半轴, c半焦距,e离心率;
e
顶点、中心
对称轴
范围、对称性、顶点、离心率
(a>0,b>0)
椭圆的基本要素:
焦点、
a、b、c、
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
