第二十二章《二次函数》章末检测(含答案) 2023-2024学年人教版九年级上册数学
文档属性
| 名称 | 第二十二章《二次函数》章末检测(含答案) 2023-2024学年人教版九年级上册数学 | 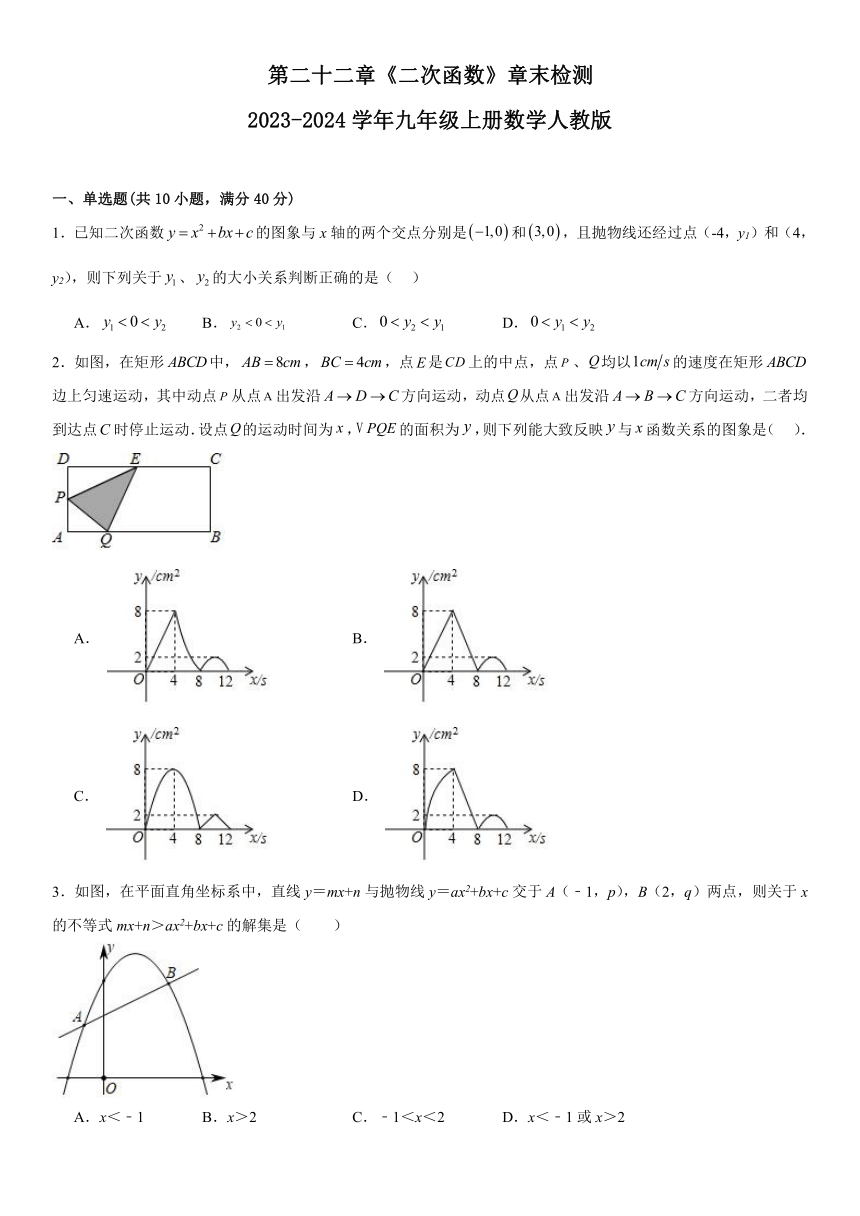 | |
| 格式 | docx | ||
| 文件大小 | 297.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 16:37:32 | ||
图片预览



文档简介
第二十二章《二次函数》章末检测
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.已知二次函数的图象与x轴的两个交点分别是和,且抛物线还经过点(-4,y1)和(4,y2),则下列关于、的大小关系判断正确的是( )
A. B. C. D.
2.如图,在矩形中,,,点是上的中点,点、均以的速度在矩形边上匀速运动,其中动点从点出发沿方向运动,动点从点出发沿方向运动,二者均到达点时停止运动.设点的运动时间为,的面积为,则下列能大致反映与函数关系的图象是( ).
A. B.
C. D.
3.如图,在平面直角坐标系中,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(2,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是( )
A.x<﹣1 B.x>2 C.﹣1<x<2 D.x<﹣1或x>2
4.已知点、、在抛物线上,则、、的大小关系是( )
A. B. C. D.
5.在函数为常数的图象上有三个点,,,则函数值,,的大小关系为( )
A. B. C. D.
6.抛物线的顶点为,与轴交于点,则该抛物线的解析式为( )
A. B.
C. D.
7.已知点, 都在的数的图像上,则( )
A. B. C. D.
8.三角形的一边长与这边上的高都为xcm,其面积是ycm2 , 则y与x的函数关系为( )
A.y=x2 B.y=2x2
C.y= x2 D.y= x2
9.已知抛物线y=x2+bx+c的顶点在第三象限,则关于x的一元二次方程x2+bx+c=0根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
10.已知抛物线与轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在轴左侧;
②;
③关于的方程无实数根;
④.
其中,正确的结论有( ).
A.1个 B.2个 C.3个 D.4
二、填空题(共8小题,满分32分)
11.已知方程,请你通过变形把它写成一个你所熟悉的函数表达式的形式,则函数表达式为 ,成立的条件是 ,是 函数.
12.已知二次函数图象的对称轴是直线,且图象过点和点,则此函数的解析式为 .
13.当或者时,代数式的值相等,则时,代数式的值为 .
14.已知二次函数 的部分图象如图所示,则关于的一元二次方程的解为 .
15.若二次函数的图象关于轴对称,则的值为: .此函数图象的顶点和它与轴的两个交点所确定的三角形的面积为: .
16.点A(x1,y1)、B(x2,y2)在二次函数的图象上,若x2>x1≥m,有y2>y1,则m的取值范围为 .
17.铅球运行高度(单位:)与水平距离(单位:)之间的函数关系满足,此运动员能把铅球推出 .
18.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表,则关于x的方程ax2+bx+c=0的解是 .
x … -5 -4 -3 -2 …
y … 4 0 -2 -2 …
三、解答题(共6小题,每题8分,满分48分)
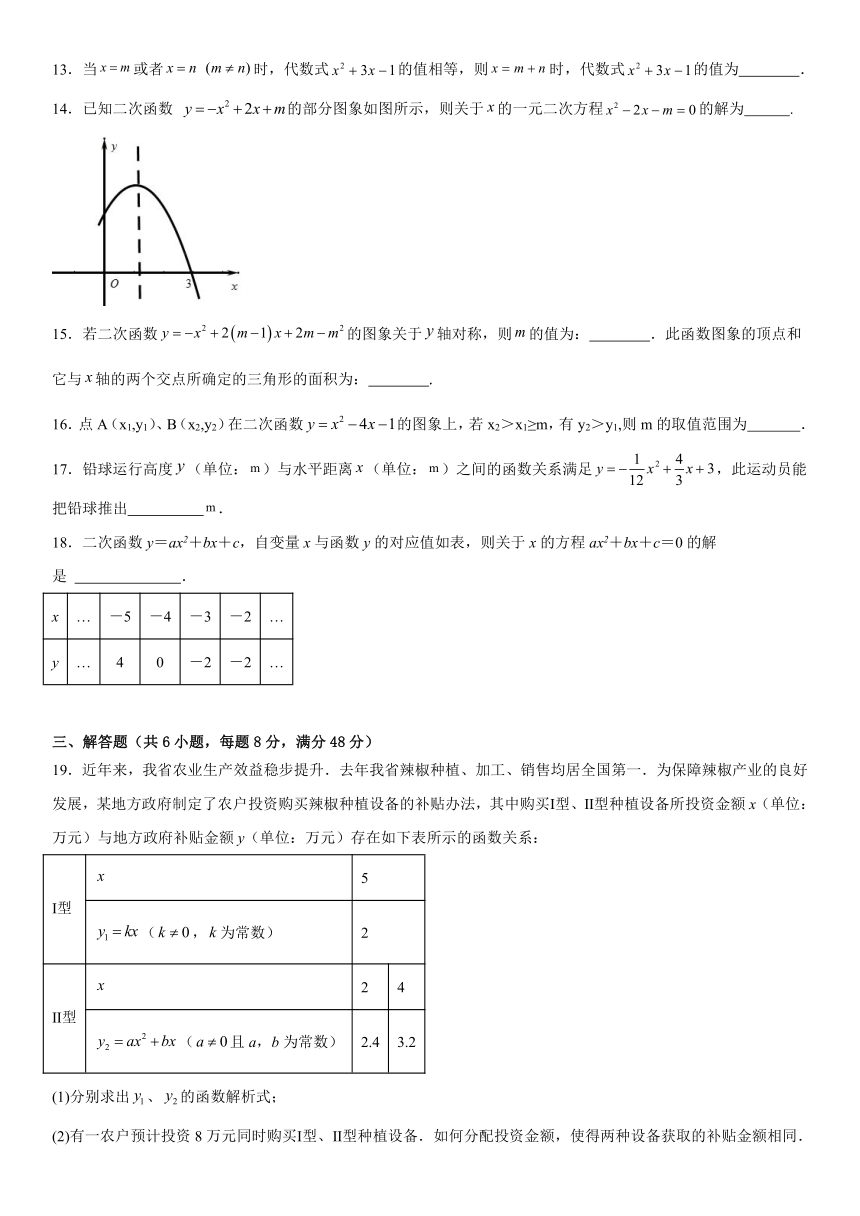
19.近年来,我省农业生产效益稳步提升.去年我省辣椒种植、加工、销售均居全国第一.为保障辣椒产业的良好发展,某地方政府制定了农户投资购买辣椒种植设备的补贴办法,其中购买Ⅰ型、Ⅱ型种植设备所投资金额x(单位:万元)与地方政府补贴金额y(单位:万元)存在如下表所示的函数关系:
Ⅰ型 5
(,为常数) 2
Ⅱ型 2 4
(且a,b为常数) 2.4 3.2
(1)分别求出、的函数解析式;
(2)有一农户预计投资8万元同时购买Ⅰ型、Ⅱ型种植设备.如何分配投资金额,使得两种设备获取的补贴金额相同.
20.春节前,某超市从厂家购进某商品,已知该商品每个的成本价为30元,经市场调查发现,该商品每天的销售量 (个)与销售单价 (元) 之间满足一次函数关系,当该商品每个售价为40元时,每天可卖出300个;当该商品每个售价为60元时,每天可卖出100个.
(1)与之间的函数关系式为__________________(不要求写出的取值范围) ;
(2)若超市老板想达到每天不低于220个的销售量,则该商品每个售价定为多少元时,每天的销售利润最大 最大利润是多少元
21.如图,抛物线与y轴交于点,与x轴交于点,点.
(1)求抛物线的解析式;
(2)当时,函数y的取值范围是 ;
(3)若点M是抛物线上的一动点,且在直线BC的上方,当取得最大值时,求的最大值和点M的坐标.
22.二次函数图象的对称轴在y轴的右侧.
(1)当时,直接写出二次函数图象的顶点坐标;
(2)探究该二次函数的图象是否过定点;
(3)若点在该二次函数的图象上,且.若过点作x轴垂线,与二次函数的交点在x轴的上方,求m的取值范围.
23.为增加农民收入,助力乡村振兴,某驻村干部指导农户进行草莓种植和销售.已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量(千克)与销售单价(元/千克)()满足的函数图象如图所示.
(1)根据图象信息,求与的函数表达式();
(2)当草莓的销售单价定为30元/千克时,求草莓的销售量的值;
(3)求当销售单价(元/千克)满足()时销售草莓获得的最大利润.
24.直线y=-3x+3与x轴、y轴分别交于A、B两点,点A关于直线x=-1的对称点为点C.
(1)求点C的坐标;
(2)若抛物线(m≠0)经过A、B、C三点,求抛物线的表达式;
(3)若抛物线(a≠0)经过A,B两点,且顶点在第二象限.抛物线与线段AC有两个公共点,求a的取值范围.
参考答案:
1.C
2.D
3.D
4.A
5.A
6.A
7.D
8.C
9.A
10.D
11. a、c均不为0 二次
12.
13.-1
14.
15. 1 1
16.m≥2.
17.18
18.x1= -4,x2= -1
19.(1),;
(2)投入Ⅰ型6万元,投入Ⅱ型2万元.
20.(1);(2)该商品每个售价定为48元时,每天的销售利润最大,最大利润是3960元
21.(1);(2);(3)最大值为20,
22.(1)
(2)过定点
(3)
23.(1)
(2)126
(3)3840元
24.(1)(-3,0)(2) (3)a<-3
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.已知二次函数的图象与x轴的两个交点分别是和,且抛物线还经过点(-4,y1)和(4,y2),则下列关于、的大小关系判断正确的是( )
A. B. C. D.
2.如图,在矩形中,,,点是上的中点,点、均以的速度在矩形边上匀速运动,其中动点从点出发沿方向运动,动点从点出发沿方向运动,二者均到达点时停止运动.设点的运动时间为,的面积为,则下列能大致反映与函数关系的图象是( ).
A. B.
C. D.
3.如图,在平面直角坐标系中,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(2,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是( )
A.x<﹣1 B.x>2 C.﹣1<x<2 D.x<﹣1或x>2
4.已知点、、在抛物线上,则、、的大小关系是( )
A. B. C. D.
5.在函数为常数的图象上有三个点,,,则函数值,,的大小关系为( )
A. B. C. D.
6.抛物线的顶点为,与轴交于点,则该抛物线的解析式为( )
A. B.
C. D.
7.已知点, 都在的数的图像上,则( )
A. B. C. D.
8.三角形的一边长与这边上的高都为xcm,其面积是ycm2 , 则y与x的函数关系为( )
A.y=x2 B.y=2x2
C.y= x2 D.y= x2
9.已知抛物线y=x2+bx+c的顶点在第三象限,则关于x的一元二次方程x2+bx+c=0根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
10.已知抛物线与轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在轴左侧;
②;
③关于的方程无实数根;
④.
其中,正确的结论有( ).
A.1个 B.2个 C.3个 D.4
二、填空题(共8小题,满分32分)
11.已知方程,请你通过变形把它写成一个你所熟悉的函数表达式的形式,则函数表达式为 ,成立的条件是 ,是 函数.
12.已知二次函数图象的对称轴是直线,且图象过点和点,则此函数的解析式为 .
13.当或者时,代数式的值相等,则时,代数式的值为 .
14.已知二次函数 的部分图象如图所示,则关于的一元二次方程的解为 .
15.若二次函数的图象关于轴对称,则的值为: .此函数图象的顶点和它与轴的两个交点所确定的三角形的面积为: .
16.点A(x1,y1)、B(x2,y2)在二次函数的图象上,若x2>x1≥m,有y2>y1,则m的取值范围为 .
17.铅球运行高度(单位:)与水平距离(单位:)之间的函数关系满足,此运动员能把铅球推出 .
18.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表,则关于x的方程ax2+bx+c=0的解是 .
x … -5 -4 -3 -2 …
y … 4 0 -2 -2 …
三、解答题(共6小题,每题8分,满分48分)
19.近年来,我省农业生产效益稳步提升.去年我省辣椒种植、加工、销售均居全国第一.为保障辣椒产业的良好发展,某地方政府制定了农户投资购买辣椒种植设备的补贴办法,其中购买Ⅰ型、Ⅱ型种植设备所投资金额x(单位:万元)与地方政府补贴金额y(单位:万元)存在如下表所示的函数关系:
Ⅰ型 5
(,为常数) 2
Ⅱ型 2 4
(且a,b为常数) 2.4 3.2
(1)分别求出、的函数解析式;
(2)有一农户预计投资8万元同时购买Ⅰ型、Ⅱ型种植设备.如何分配投资金额,使得两种设备获取的补贴金额相同.
20.春节前,某超市从厂家购进某商品,已知该商品每个的成本价为30元,经市场调查发现,该商品每天的销售量 (个)与销售单价 (元) 之间满足一次函数关系,当该商品每个售价为40元时,每天可卖出300个;当该商品每个售价为60元时,每天可卖出100个.
(1)与之间的函数关系式为__________________(不要求写出的取值范围) ;
(2)若超市老板想达到每天不低于220个的销售量,则该商品每个售价定为多少元时,每天的销售利润最大 最大利润是多少元
21.如图,抛物线与y轴交于点,与x轴交于点,点.
(1)求抛物线的解析式;
(2)当时,函数y的取值范围是 ;
(3)若点M是抛物线上的一动点,且在直线BC的上方,当取得最大值时,求的最大值和点M的坐标.
22.二次函数图象的对称轴在y轴的右侧.
(1)当时,直接写出二次函数图象的顶点坐标;
(2)探究该二次函数的图象是否过定点;
(3)若点在该二次函数的图象上,且.若过点作x轴垂线,与二次函数的交点在x轴的上方,求m的取值范围.
23.为增加农民收入,助力乡村振兴,某驻村干部指导农户进行草莓种植和销售.已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量(千克)与销售单价(元/千克)()满足的函数图象如图所示.
(1)根据图象信息,求与的函数表达式();
(2)当草莓的销售单价定为30元/千克时,求草莓的销售量的值;
(3)求当销售单价(元/千克)满足()时销售草莓获得的最大利润.
24.直线y=-3x+3与x轴、y轴分别交于A、B两点,点A关于直线x=-1的对称点为点C.
(1)求点C的坐标;
(2)若抛物线(m≠0)经过A、B、C三点,求抛物线的表达式;
(3)若抛物线(a≠0)经过A,B两点,且顶点在第二象限.抛物线与线段AC有两个公共点,求a的取值范围.
参考答案:
1.C
2.D
3.D
4.A
5.A
6.A
7.D
8.C
9.A
10.D
11. a、c均不为0 二次
12.
13.-1
14.
15. 1 1
16.m≥2.
17.18
18.x1= -4,x2= -1
19.(1),;
(2)投入Ⅰ型6万元,投入Ⅱ型2万元.
20.(1);(2)该商品每个售价定为48元时,每天的销售利润最大,最大利润是3960元
21.(1);(2);(3)最大值为20,
22.(1)
(2)过定点
(3)
23.(1)
(2)126
(3)3840元
24.(1)(-3,0)(2) (3)a<-3
同课章节目录
