13.3.1等腰三角形 课时练习(含答案) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 13.3.1等腰三角形 课时练习(含答案) 2023-2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 328.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 16:56:03 | ||
图片预览



文档简介
等腰三角形
一、单选题
1、等腰三角形有一个角是,则另两个角分别是( )
A. B. C. D.
2、若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )
A.2cm B.4cm C.6cm D.8cm
3、已知等腰三角形的两边长分别是3,7,则这个等腰三角形的周长为( )
A.11 B.13 C.17 D.13或17
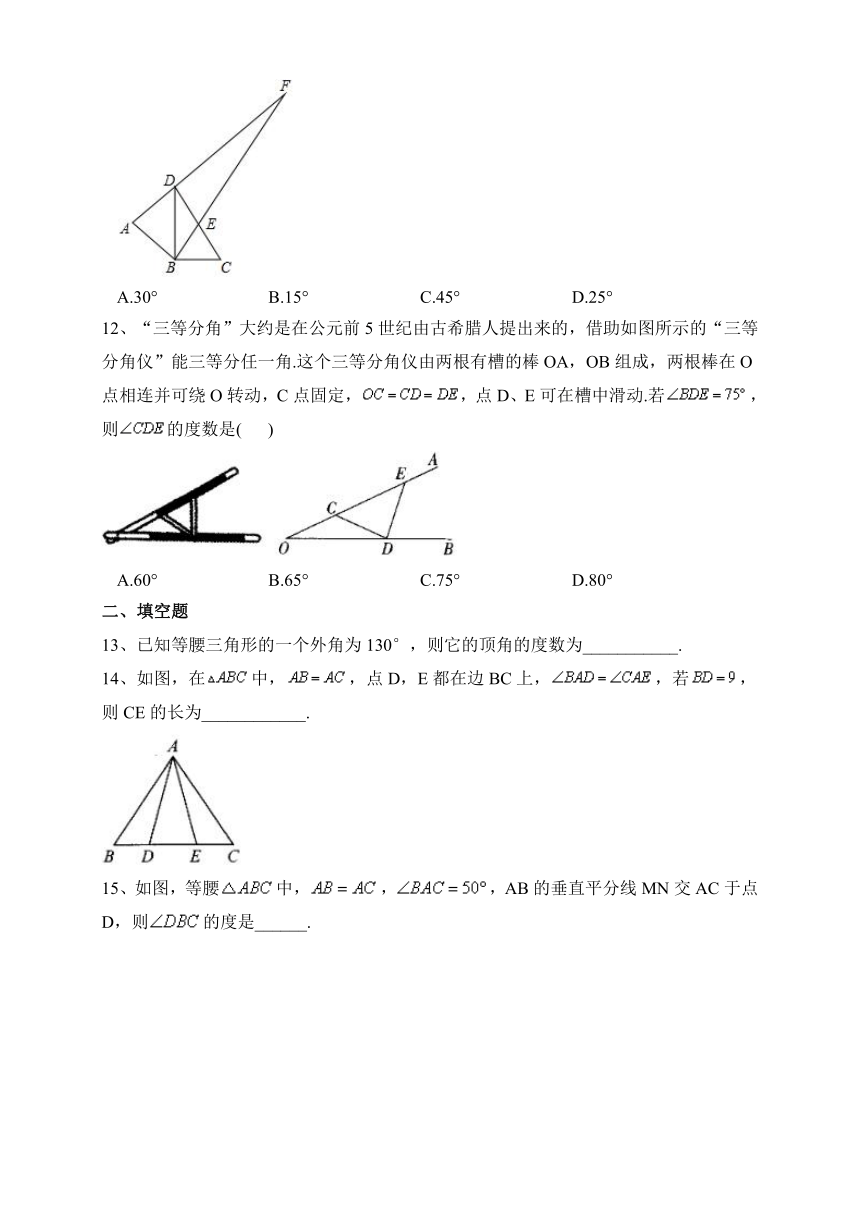
4、如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形ABC,若,D是BC的中点,,则AD的长为( )
A. B. C. D.
5、如图,在中,D为BC边上一点,,,则的度数为( )
A. B. C. D.
6、如图,等腰中,点D,E分别在腰AB,AC上,添加下列条件,不能判定的是( )
A. B. C. D.
7、如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则周长的最小值为( )
A.6 B.8 C.10 D.12
8、如图,在中,点D和E分别在AB和AC上,且.连接DE,过点A的直线GH与DE平行,若,则的度数为( )
A.40° B.45° C.55° D.70°
9、如图,已知中,,P为内一点,过点P的直线MN分别交AB,BC于点M,N.若M在PA的垂直平分线上,N在PC的垂直平分线上,则的度数为( )
A.100° B.105° C.115° D.无法确定
10、如图,点A在DE上,且,,则DE等于( )
A.DC B.BC C.AB D.
11、如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,中点为与BE的延长线交于点F,则的度数为( )
A.30° B.15° C.45° D.25°
12、“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,,点D、E可在槽中滑动.若,则的度数是( )
A.60° B.65° C.75° D.80°
二、填空题
13、已知等腰三角形的一个外角为130°,则它的顶角的度数为___________.
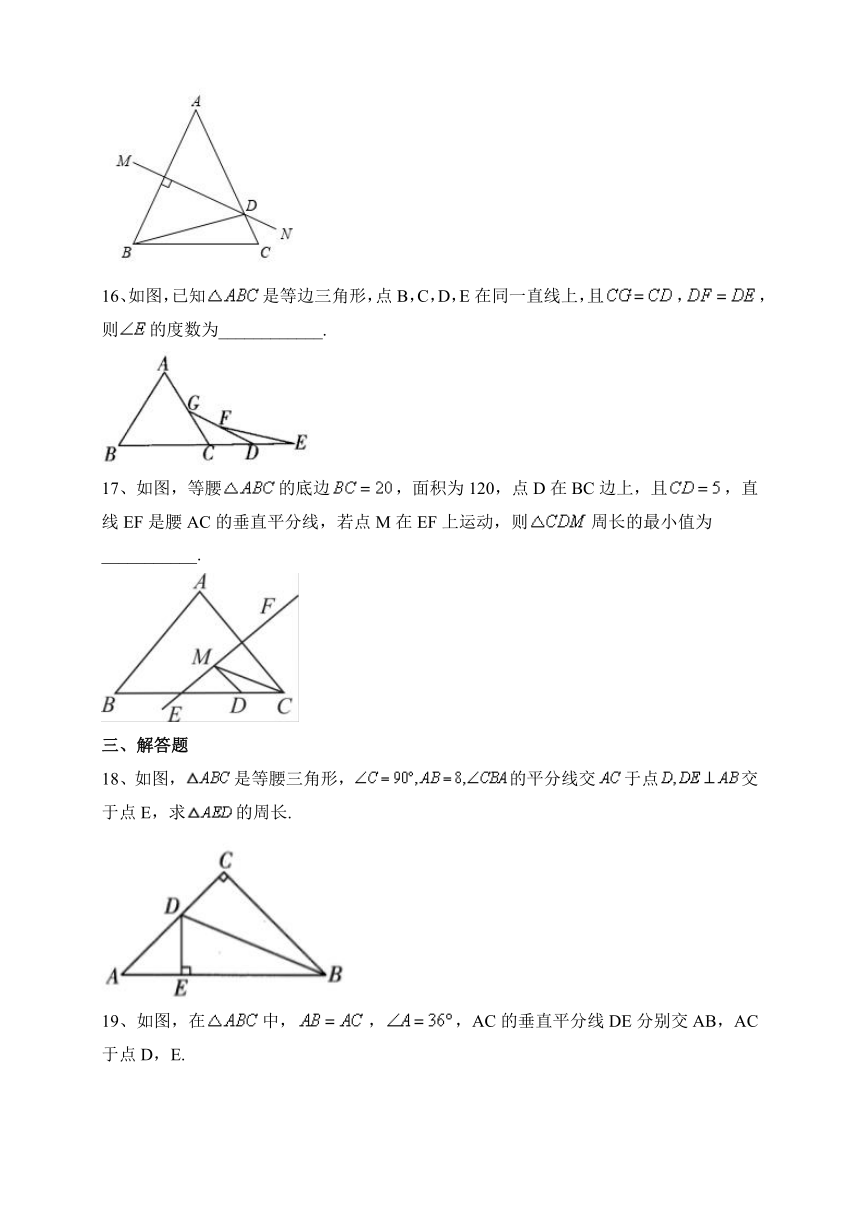
14、如图,在中,,点D,E都在边BC上,,若,则CE的长为____________.
15、如图,等腰中,,,AB的垂直平分线MN交AC于点D,则的度是______.
16、如图,已知是等边三角形,点B,C,D,E在同一直线上,且,,则的度数为____________.
17、如图,等腰的底边,面积为120,点D在BC边上,且,直线EF是腰AC的垂直平分线,若点M在EF上运动,则周长的最小值为___________.
三、解答题
18、如图,是等腰三角形,的平分线交于点交于点E,求的周长.
19、如图,在中,,,AC的垂直平分线DE分别交AB,AC于点D,E.
(1)求证:是等腰三角形;
(2)若的周长是13,,求AC的长.
20、如图,在中,,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若,求的度数;
(2)若,的周长为20,求的周长.
21、如图,在中,,,O为AB的中点,D,E分别在AC,BC上,且.求证:.
22、如图,在中,,D为CA延长线上一点,于点E,交AB于点F,若.
求证:
(1)是等腰三角形.
(2).
23、如图,在中,,E为边BC上的点,且,D为线段BE的中点,过点E作,过点A作,且AF,EF相交于点F.
(1)试说明:;
(2)试说明:.
24、如图,在中,,,D为BC的中点,于E,交CE的延长线于F.
(1)求证:;
(2)连接DF,求证:AB垂直平分DF.
参考答案
1、答案:B
解析:略
2、答案:A
解析:若2cm为等腰三角形的腰长,则底边长为,,不符合三角形的三边关系;
若2cm为等腰三角形的底边,则腰长为,此时三角形的三边长分别为2cm,4cm,4cm,符合三角形的三边关系;
故选A.
3、答案:C
解析:①当3是腰长时,三角形的三边长分别为3,3,7,不能组成三角形;②当3是底边长时,三角形的三边长分别为7,7,3,能组成三角形,周长.综上所述,这个等腰三角形的周长是17.
4、答案:C
解析:,D是BC的中点,,.,.
5、答案:D
解析:如图,,,.,.,,,,.
6、答案:B
解析:为等腰三角形,
,,
当时,则根据“SAS”可判断;
当,则根据“AAS”可判断;
当,则,根据“ASA”可判断.
故选:B.
7、答案:C
解析:连接AD,
是等腰三角形,点D是BC边的中点,
,
,解得,
EF是线段AC的垂直平分线,
点C关于直线EF的对称点为点A,
AD的长为的最小值,
的周长最短.
故选:C.
8、答案:C
解析:,,,,,,,故选C.
9、答案:C
解析:,,M在PA的垂直平分线上,N在PC的垂直平分线上,,,,,,,,故选C.
10、答案:C
解析:,,即.又,是等腰三角形,.,,.在和中,,,,,.故选C.
11、答案:B
解析:解:,E为DC中点,,是等腰直角三角形,,,故选B.
12、答案:D
解析:,,,,,,,.故选D.
13、答案:50°或80°
解析:由等腰三角形的一个外角为130°知一个内角为50°.当50°为顶角时,其他两个角都为65°;当50°为底角时,其他两个角为50°、80°,所以等腰三角形的顶角为50°或80°.
14、答案:9
解析:因为,所以.在和中,因为,所以.所以.
15、答案:15°
解析:,,
,
MN垂直平分线AB,
,
,
.
故答案为:15°.
16、答案:
解析:是等边三角形,.,.,.,.,.
17、答案:18
解析:如图,作于H,连接AM,
EF垂直平分线段AC,
,
,
当A、D、M共线时,的值最小,
等腰的底边,面积为120,,
,,
,
,
的最小值为13,
周长的最小值,
故答案为18.
18、答案:8
解析:略
19、答案:(1)证明见解析
(2)8
解析:(1)证明:,,
.
DE是AC的垂直平分线,
,
,
,
,
,
是等腰三角形;
(2)解:的周长是13,
,
,
,即,
,
,
.
20、答案:(1)30°
(2)32
解析:(1)在中,,,
,
AB的垂直平分线MN交AC于点D,
,
,
;
(2)MN垂直平分AB,
,
,
,
,
,
的周长.
21、答案:证明:如图,连接OC.
,O为AB的中点,
,.
,
,.
,,
.
,.
又,,
,.
,.
22、答案:(1)证明见解析
(2)证明见解析
解析:(1),.
,
,,
.
,
,,
是等腰三角形.
(2)如图,过点A作于点H,
,
.
由(1)知,
.
在和中,
.
,,.
23、答案:(1)因为,所以是等腰三角形.
又因为D为BE的中点,所以.
在和中,
因为为公共角,,
所以.
(2)因为,所以.
因为,所以.
所以.
在和中,,
所以.
所以.
24、答案:证明:(1),,
又,,
又,,
,即.
在和中,
,
.
(2)由(1)得,
D为BC的中点,,.
为等腰直角三角形,
,
,,
,
BA平分.
根据等腰三角形“三线合一”的性质得AB垂直平分DF.
一、单选题
1、等腰三角形有一个角是,则另两个角分别是( )
A. B. C. D.
2、若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )
A.2cm B.4cm C.6cm D.8cm
3、已知等腰三角形的两边长分别是3,7,则这个等腰三角形的周长为( )
A.11 B.13 C.17 D.13或17
4、如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形ABC,若,D是BC的中点,,则AD的长为( )
A. B. C. D.
5、如图,在中,D为BC边上一点,,,则的度数为( )
A. B. C. D.
6、如图,等腰中,点D,E分别在腰AB,AC上,添加下列条件,不能判定的是( )
A. B. C. D.
7、如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则周长的最小值为( )
A.6 B.8 C.10 D.12
8、如图,在中,点D和E分别在AB和AC上,且.连接DE,过点A的直线GH与DE平行,若,则的度数为( )
A.40° B.45° C.55° D.70°
9、如图,已知中,,P为内一点,过点P的直线MN分别交AB,BC于点M,N.若M在PA的垂直平分线上,N在PC的垂直平分线上,则的度数为( )
A.100° B.105° C.115° D.无法确定
10、如图,点A在DE上,且,,则DE等于( )
A.DC B.BC C.AB D.
11、如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,中点为与BE的延长线交于点F,则的度数为( )
A.30° B.15° C.45° D.25°
12、“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,,点D、E可在槽中滑动.若,则的度数是( )
A.60° B.65° C.75° D.80°
二、填空题
13、已知等腰三角形的一个外角为130°,则它的顶角的度数为___________.
14、如图,在中,,点D,E都在边BC上,,若,则CE的长为____________.
15、如图,等腰中,,,AB的垂直平分线MN交AC于点D,则的度是______.
16、如图,已知是等边三角形,点B,C,D,E在同一直线上,且,,则的度数为____________.
17、如图,等腰的底边,面积为120,点D在BC边上,且,直线EF是腰AC的垂直平分线,若点M在EF上运动,则周长的最小值为___________.
三、解答题
18、如图,是等腰三角形,的平分线交于点交于点E,求的周长.
19、如图,在中,,,AC的垂直平分线DE分别交AB,AC于点D,E.
(1)求证:是等腰三角形;
(2)若的周长是13,,求AC的长.
20、如图,在中,,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若,求的度数;
(2)若,的周长为20,求的周长.
21、如图,在中,,,O为AB的中点,D,E分别在AC,BC上,且.求证:.
22、如图,在中,,D为CA延长线上一点,于点E,交AB于点F,若.
求证:
(1)是等腰三角形.
(2).
23、如图,在中,,E为边BC上的点,且,D为线段BE的中点,过点E作,过点A作,且AF,EF相交于点F.
(1)试说明:;
(2)试说明:.
24、如图,在中,,,D为BC的中点,于E,交CE的延长线于F.
(1)求证:;
(2)连接DF,求证:AB垂直平分DF.
参考答案
1、答案:B
解析:略
2、答案:A
解析:若2cm为等腰三角形的腰长,则底边长为,,不符合三角形的三边关系;
若2cm为等腰三角形的底边,则腰长为,此时三角形的三边长分别为2cm,4cm,4cm,符合三角形的三边关系;
故选A.
3、答案:C
解析:①当3是腰长时,三角形的三边长分别为3,3,7,不能组成三角形;②当3是底边长时,三角形的三边长分别为7,7,3,能组成三角形,周长.综上所述,这个等腰三角形的周长是17.
4、答案:C
解析:,D是BC的中点,,.,.
5、答案:D
解析:如图,,,.,.,,,,.
6、答案:B
解析:为等腰三角形,
,,
当时,则根据“SAS”可判断;
当,则根据“AAS”可判断;
当,则,根据“ASA”可判断.
故选:B.
7、答案:C
解析:连接AD,
是等腰三角形,点D是BC边的中点,
,
,解得,
EF是线段AC的垂直平分线,
点C关于直线EF的对称点为点A,
AD的长为的最小值,
的周长最短.
故选:C.
8、答案:C
解析:,,,,,,,故选C.
9、答案:C
解析:,,M在PA的垂直平分线上,N在PC的垂直平分线上,,,,,,,,故选C.
10、答案:C
解析:,,即.又,是等腰三角形,.,,.在和中,,,,,.故选C.
11、答案:B
解析:解:,E为DC中点,,是等腰直角三角形,,,故选B.
12、答案:D
解析:,,,,,,,.故选D.
13、答案:50°或80°
解析:由等腰三角形的一个外角为130°知一个内角为50°.当50°为顶角时,其他两个角都为65°;当50°为底角时,其他两个角为50°、80°,所以等腰三角形的顶角为50°或80°.
14、答案:9
解析:因为,所以.在和中,因为,所以.所以.
15、答案:15°
解析:,,
,
MN垂直平分线AB,
,
,
.
故答案为:15°.
16、答案:
解析:是等边三角形,.,.,.,.,.
17、答案:18
解析:如图,作于H,连接AM,
EF垂直平分线段AC,
,
,
当A、D、M共线时,的值最小,
等腰的底边,面积为120,,
,,
,
,
的最小值为13,
周长的最小值,
故答案为18.
18、答案:8
解析:略
19、答案:(1)证明见解析
(2)8
解析:(1)证明:,,
.
DE是AC的垂直平分线,
,
,
,
,
,
是等腰三角形;
(2)解:的周长是13,
,
,
,即,
,
,
.
20、答案:(1)30°
(2)32
解析:(1)在中,,,
,
AB的垂直平分线MN交AC于点D,
,
,
;
(2)MN垂直平分AB,
,
,
,
,
,
的周长.
21、答案:证明:如图,连接OC.
,O为AB的中点,
,.
,
,.
,,
.
,.
又,,
,.
,.
22、答案:(1)证明见解析
(2)证明见解析
解析:(1),.
,
,,
.
,
,,
是等腰三角形.
(2)如图,过点A作于点H,
,
.
由(1)知,
.
在和中,
.
,,.
23、答案:(1)因为,所以是等腰三角形.
又因为D为BE的中点,所以.
在和中,
因为为公共角,,
所以.
(2)因为,所以.
因为,所以.
所以.
在和中,,
所以.
所以.
24、答案:证明:(1),,
又,,
又,,
,即.
在和中,
,
.
(2)由(1)得,
D为BC的中点,,.
为等腰直角三角形,
,
,,
,
BA平分.
根据等腰三角形“三线合一”的性质得AB垂直平分DF.
